本文来自“单细胞组学”公众号 原文链接：https://mp.weixin.qq.com/s/mfu3jsTv6Nk85yNnLQS_zw

2020年将尽，让我们把今年所有不愉快都抹去，开启新年新旅程。本次的单细胞算法分享也回归到数据分析的起点，单细胞数据标准化。

单细胞数据标准化有两大思路：

  1. Log标准化。类似于bulk RNAseq，用每个样本（细胞）的总体reads数附带测序深度的权重值衡量，再取log标准化基因的表达量；
  2. 基于概率统计的方法标准化。如泊松分布，负二项分布等。

    1. Log标准化

    Log标准化想必是大家用的最多的方法，在R包Seurat的函数LogNormalize就是这一类方法[1]。具体处理方式是，在每个细胞中，每个基因除以这一个细胞中所有基因reads数，然后乘以一个固定的数值（测序深度权重），最后取log，得到每个基因的标准化表达量。如下图所示，虽然a, b, c三个细胞的原始reads数不同，但它们是同一种细胞。Reads数的不同是由于实验和测序技术等因素造成的细胞reads检测总数差异，可以用Log标准化抵消，最后得到一致的表达量。
    单细胞转录组数据特征与标准化（一）：泊松分布和准泊松回归 - 图1
    具体实现代码如下： ```python

    R

    LogNormalize <- function(data){ data_log <- apply(data,2,function(x)log(x/sum(x)*10000+1)) return(data_log) }

python

def normalize(data): mat_log = data.apply(lambda x:np.log(x/sum(x)*10000+1)) return(mat_log)

  1. Log标准化方法类似于CPM。CPM的计算方法如下：<br />CPM=total exon reads / mapped reads (Millions)<br />CPM计算方法不同的地方在于，系数是一百万而不是一万；没有取log。
  2. <a name="XX0Nm"></a>
  3. ## 2. 概率统计标准化
  4. 在介绍应用方法之前，我们先看看单细胞数据的特征。<br />对于大多数基于UMI count建库测序的单细胞数据，每个基因原始reads数的分布近似于**泊松分布**或者**负二项分布**[2]。<br />我们可以用10X官网的测试数据pbmc看看[3]。下图展示基因ACTB在两千多个细胞中的reads数分布。<br />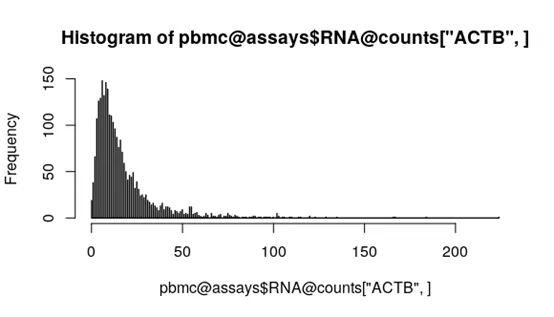![](https://cdn.nlark.com/yuque/0/2021/webp/655888/1638529005740-98335c5d-e246-4a30-8809-035c363c5990.webp#clientId=u25bca038-d7c2-4&crop=0&crop=0&crop=1&crop=1&from=paste&id=u5aafeb97&margin=%5Bobject%20Object%5D&originHeight=317&originWidth=554&originalType=url&ratio=1&rotation=0&showTitle=false&status=done&style=none&taskId=u8826455d-0fd8-4432-84cc-db3d2955630&title=)<br />对于其他类型的测序数据，泊松分布和负二项分布的拟合效果差[4]。如下图所示CEL-Seq，Drop-Seq等数据有70%以上概率符合泊松分布和负二项分布，而基于平板的测序技术如Smart-Seq2拟合效果差。<br />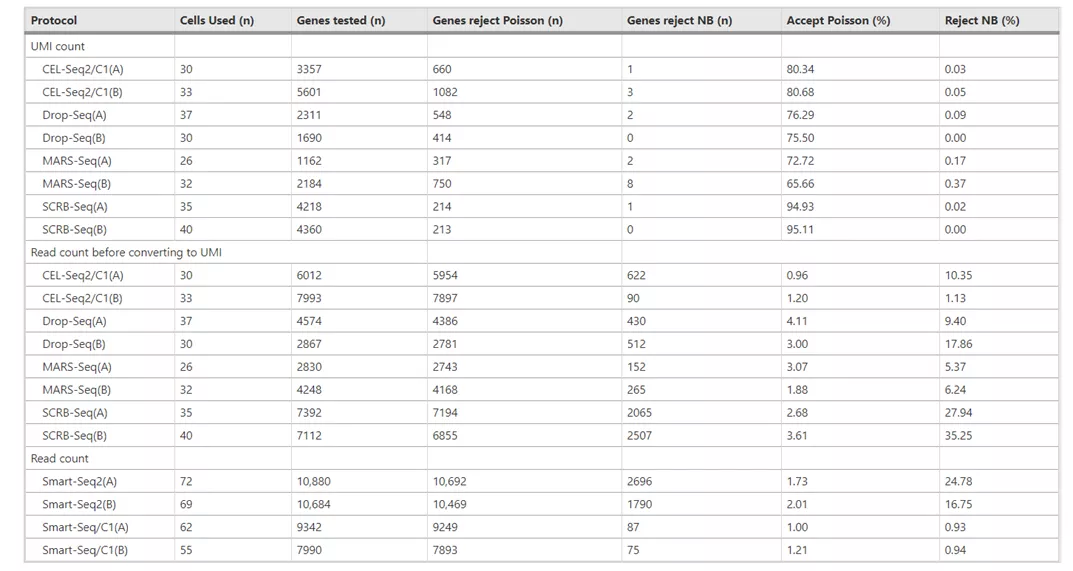![](https://cdn.nlark.com/yuque/0/2021/webp/655888/1638529005790-4f923e85-7ea9-4973-af09-1fb85d5492af.webp#clientId=u25bca038-d7c2-4&crop=0&crop=0&crop=1&crop=1&from=paste&id=ua8e9f111&margin=%5Bobject%20Object%5D&originHeight=571&originWidth=1073&originalType=url&ratio=1&rotation=0&showTitle=false&status=done&style=none&taskId=ub613f118-87c3-4d13-b1ee-1f3dc4f422e&title=)<br />我们**假定10X的reads数服从泊松分布**，接下来可以**用泊松回归分析**看看测序深度与某一基因reads数的关系。
  6. 我们将pbmc数据中ACTB在不同细胞的reads数作为因变量，把每个细胞的总reads数作为自变量，拟合泊松回归：
  7. ```python
  9. data_step <- data.frame(log10_umi = log10(pbmc@meta.data$nCount_RNA),
  10.                          ACTB = as.matrix(pbmc@assays$RNA@counts['ACTB',]),
  11.                          stringsAsFactors = F)
  12. fit4 <- glm(ACTB~log10_umi, family = poisson, data = data_step)
  13. exp(coef(fit4))
  14. (Intercept)    log10_umi
  15. 1.161727e-04 3.354639e+01

从结果可以看出，当细胞的log10（总reads数）增加34，ACTB基因的reads数增加1。R包SCTranform就是基于这一思想进行单细胞数据标准化。

泊松分布的方差与均值相等，当观测值的方差与泊松分布拟合的方差大时，泊松回归可能出现过度离势（overdispersion）。可以用准泊松回归（quasi-poisson regression）可以解决这种情况。用R包qcc中的overdispersion函数可以检测过度离势。pbmc的检测结果中有接近6906个基因泊松回归存在过度离势的情况。

  2. library(qcc)
  3. library(pbapply)
  4. overdispersion <-pbsapply(1:nrow(pbmc), function(x) {
  5.    qcc.overdispersion.test(as.matrix(pbmc@assays$RNA@counts[x,],type = 'poisson'))})
  6. |++++++++++++++++++++++++++++++++++++++++++++++++++| 100% elapsed=01m14s
  7. overdispersion <-t(overdispersion)
  8. sum(overdispersion[,3] >= 0.05)
  9. [1] 6906

所以用准泊松回归代替泊松回归比较妥当。

1
2

fit4 <- glm(ACTB~log10_umi, family = quasipoisson, data = data_step)

那么准泊松分布回归和负二项分布回归哪种方法更适合过度离势的单细胞数据？虽然这两种方法的效果类似，但有研究表明，负二项分布回归注重表达量比较小的基因，而准泊松分布回归注重表达量比较大的基因[3]。方法的选择看数据类型与关注的要点。

下期内容预告：单细胞转录组数据特征与标准化（二）：SCTransform.
届时将用R的基础函数一步步实现SCTransform的标准化过程，并比较log标准化和基于概率统计标准化SCTranform的异同。

参考链接：
[1]. Stuart T, Butler A, Hoffman P, Hafemeister C, Papalexi E, III WMM, Hao Y, Stoeckius M, Smibert P, Satija R (2019). “Comprehensive Integration of Single-Cell Data.” Cell, 177, 1888-1902.
[2]. Chen, Wenan, et al. “UMI-count modeling and differentialexpression analysis for single-cell RNA sequencing.” Genome biology 19.1 (2018): 70.
[3]. https://cf.10xgenomics.com/samples/cell/pbmc3k/pbmc3k_filtered_gene_bc_matrices.tar.gz
[4]. Ver Hoef, Jay M., and Peter L. Boveng. “Quasi‐Poisson vs. negativebinomial regression: how should we model overdispersed count data?.” Ecology 88.11 (2007): 2766-2772.