本文来自“单细胞组学”公众号 原文链接:https://mp.weixin.qq.com/s/33nj9ShPrpeaUYBT-1dAqQ
一个单细胞转录组样本通常含有成千上万个基因,为了直观了解不同细胞样本之间的联系,常用降低基因维度的手段,对多维数据进行可视化。
降维是对单细胞表达矩阵进行矩阵分解的过程,常见的如PCA(主成分分析)的特征值分解,而SVD分解是另一种重要的矩阵分解,它与矩阵的特征分解关系密切,在统计分析与信号处理等方面具有重要作用,本文将详细介绍SVD分解的推导及其应用。
1. 矩阵乘法
我们学习线性代数时,是通过解线性方程组来引入矩阵的乘法运算的。比如: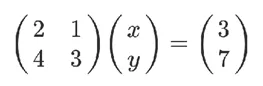
这个矩阵的乘法运算实际上就是方程组:
2x+y=3
4x+3y=7
的矩阵乘法形式。事实上,矩阵的乘法可以用如下公式表示(小伙伴们应该很熟悉这个公式):
Ax=b
这个公式内容其实很丰富,解线性方程组时,x与b就是向量。当满足上述公式的x,b是矩阵时,我们可以看到b矩阵可以由两个(多个)矩阵的相乘而得,这就是矩阵分解。通过将目标矩阵分解为几个特殊形式的矩阵相乘,可以让矩阵的计算更加方便。
2. 矩阵的特征分解
矩阵A(n*n)满足下列式子:
Ax=λx
则λ为A的特征值,x是A的特征向量。
我们重新来看Ax=b这个公式,矩阵A可以理解为一种变化,这种变化使得向量x变成了向量b。
上图展示了代表不同变化的矩阵A
在特征值分解中,实际上是利用矩阵A对x进行了伸缩(λ)变化。于是:
Ax1=λ1x1
Ax2=λ2x2
Ax3=λ3x3
…
Axn=λnxn
我们利用特征值与特征向量来表示A:
AW=WΣ
A=WΣW−1
A的特征向量(前提n个列向量线性无关)构成矩阵W{w1,w2,…wn},Σ 为这n个特征值为主对角线的n×n维矩阵.上述公式就是矩阵的对角化,矩阵A与对角矩阵Σ相似,具有相同的特征值。
可以对A的列向量进行标准化处理(向量平方和等于1,即W1TW1=1),比如:(1,1)=>(1/21/2,1/21/2),由于A的各列向量线性无关,因此,经过标准化之后的W,其列向量(标准化之后的A的特征向量)就成为了标准正交基。W是一个正交矩阵,于是WTW=I,WT=W-1。于是特征分解表示为:
A=WΣW−1 <=>A=WΣWT
明确了矩阵A的特征值与特征向量之后,矩阵A就可用三个由它们构成的矩阵的乘积来表示了。这就是矩阵的特征分解。
那么特征分解与SVD(奇异值分解)有什么关系呢?你是否注意到,矩阵特征分解的前提条件是什么?没错,A必须是一个方阵。在实际应用中,相关数据抽象成的矩阵很大概率并不是一个方阵,那该怎么办?
3. SVD概念
SVD也就是奇异值分解,顾名思义也是一种对矩阵的分解。SVD的定义如下:
A=UΣVT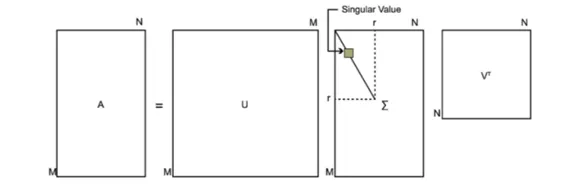
如图所示,矩阵A是一个mn的矩阵,U是一个mm方阵,Σ是一个m×n的矩阵,主对角线为奇异值,其他元素全为0,V是一个n*n的方阵,同特征分解一样,U与V也是一个正交矩阵。
事实上,矩阵的奇异值分解算是特征值分解的延伸,当m=n时,奇异值分解就变成了特征值分解。
4. 推导与计算
对于非方阵A(mn),我们常用的方法就是将A与A的转置相乘从而得到一个方阵。ATA构成一个nn矩阵,AAT构成一个mm方阵。对于方阵,我们可以运用特征分解,于是得到下列两个公式:
(ATA)vi=λivi
(AAT)ui=λiui
如此,根据之前提到的特征分解的方法,我们可以得到ATA n阶方阵的特征向量,这些特征向量就构成了奇异值分解中的V。同理,AAT m阶方阵的特征向量构成了奇异值分解中的U。
上述结论证明如下:
根据U,V是正交矩阵,满足U-1=UT,V-1=VT,ΣTΣ=Σ2
A=UΣVT ⇒ AT=VΣTUT ⇒ ATA=VΣTUTUΣVT=VΣ2VT
A=UΣVT ⇒ AT=VΣTUT ⇒ AAT=UΣVTVΣTUT=UΣ2UT
故:
n阶方阵AAT的特征值=奇异值平方
m阶方阵ATA的特征值=奇异值平方
奇异值的数目应该与m与n较小值相同。
奇异值σi的计算公式:
σi=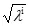
5. 实例

6. SVD的性质与应用
我们发现,奇异值与特征值类似,在奇异值矩阵中也是按照从大到小排列,而且奇异值减小的速度很快,在多数情况下,前10%的奇异值的和就占了全部的奇异值之和的99%以上的比例。因此我们可以用最大的k个的奇异值和对应的左右奇异向量来近似描述矩阵,如:
Am×n=Um×mΣm×nVTn×n≈Um×kΣk×kVTk×n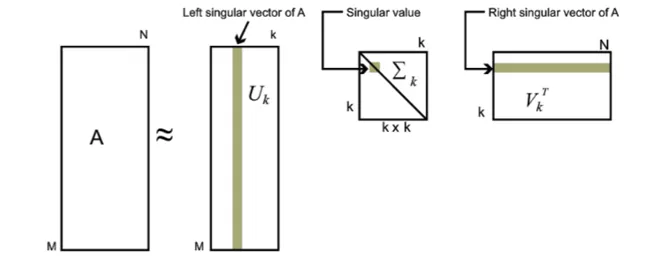
图中所示:k要比n小很多,也就是一个大的矩阵A可以用三个小的矩阵Um×k,Σk×k,VTk×n来表示。现在我们的矩阵A只需要灰色的部分的三个小矩阵就可以近似描述了。
这个性质让SVD在图片压缩与去燥领域发挥很大的作用。
SVD在PCA中的应用:
主成分分析(Principal Component Analysis,PCA)的目标是用一组较少的不相关的变量代替大量相关变量,同时尽可能保留原始变量的信息,推导所得的变量就成为主成分,是原始变量的线性组合。也就是将N个变量(N维),通过线性组合,降维到K个综合变量(K维,K 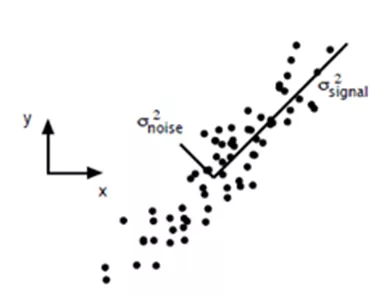
PCA降维的算法如下:
输入:n维样本集D=(x(1),x(2),…,x(m)),要降维到的维数n’
输出:降维后的样本集D’
1) 对所有的样本进行中心化: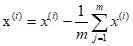
2) 计算样本的协方差矩阵XXT
3) 对矩阵XXT进行特征值分解
4)取出最大的n’个特征值对应的特征向量(w1,w2,…,wn′), 将所有的特征向量标准化后,组成特征向量矩阵W。
5)对样本集中的每一个样本x(i),转化为新的样本z(i)=WTx(i)
6) 得到输出样本集D’=(z(1),z(2),…,z(m))
根据上述算法,用PCA降维时,需要找到样本协方差矩阵XTX的最大的d个特征向量,然后用这最大的d个特征向量构成的矩阵来与原高维数据相乘达到低维投影降维的目的。事实上,由于得到协方差矩阵的特征值特征向量有两种方法:特征值分解、奇异值分解,故PCA算法也有两种实现方法:基于特征值分解协方差矩阵实现PCA算法、基于SVD分解协方差矩阵实现PCA算法。当样本数多样本特征数也多的时候,协方差矩阵计算量很大。而目前存在一些SVD算法(LAPACK solver:http://www.netlib.org/lapack/lapack-3.6.0.html;randomized SVD:https://arxiv.org/abs/0909.4061;scikit-learn的PCA算法)可以在不求出协方差矩阵的情况下,也能求出我们的右奇异矩阵V,从而避免了大量运算。也就是说,对于大数据集,我们的PCA算法的实现可以不用做特征分解,而是做SVD来完成。
单细胞RNA数据完美符合了大数据集的特点,目前单细胞研究的数据动辄是由上万甚至十万的细胞数与上万的基因数构成的超大矩阵。因此单细胞RNA数据的分析基本少不了用基于SVD的PCA来降维。
假设我们的样本是m×n的矩阵X,如果我们通过SVD找到了矩阵XXT最大的d个特征向量张成的m×d维矩阵U,则我们如果进行如下处理:
X’d×n=UTd×mXmxn
得到一个d×n的矩阵X’,这个矩阵和我们原来的m×n维样本矩阵X相比,行数从m减到了d,可见对行数进行了压缩。也就是说,左奇异矩阵可以用于行数的压缩。相对的,右奇异矩阵可以用于列数的压缩。单细胞RNA数据的表达量矩阵通常是行代表基因,列代表细胞。因此,上述对行的压缩处理就实现了降维。
举个例子,在实际的单细胞RNA-seq项目中,我们经常做的是根据每个细胞的基因表达水平,对细胞进行聚类,试图发现新的细胞类型及其标记基因。比如在研究胚胎发育不同时期细胞的基因表达模式,探明这些细胞样本的分期是受哪些基因的调控,通过对受精卵、2细胞胚、4细胞胚、8细胞胚、桑椹胚、囊胚等细胞样品做单细胞RNA测序。
经过RNA测序样本比对与定量,我们可以得到一个(m*n)的大型矩阵,m代表基因数,n代表细胞数。PCA分析中,我们通常以基因为变量,对样本进行聚类,通过PC的选择便可以发现究竟是哪些基因对细胞分型具有重要意义。
参考资料:
1. [美]戴维 C.雷线性代数及其应用第四版
2. https://www.cnblogs.com/pinard/p/6251584.html
3. http://www.cnblogs.com/pinard/p/6239403.html
4. http://www.cnblogs.com/LeftNotEasy/archive/2011/01/19/svd-and-applications.html
5. https://www.cnblogs.com/AndyJee/p/3846455.html
6. https://blog.csdn.net/u010945683/article/details/45972819
7. Yan, L., Yang, M., Guo, H., Yang, L., Wu, J., Li, R., … &Huang, J.(2013). Single-cell RNA-Seq profiling of human preimplantationembryos and embryonic stem cells. Nature structural & molecularbiology, 20(9), 1131.

