单细胞转录组数据特征与标准化（二）：sctransform原理解析与标准化方法的选择

本文来自“单细胞组学”公众号 原文链接：https://mp.weixin.qq.com/s/M-Y56hGtxTgYc7G8WH-zGA

上一期主要描述了Log标准化方法和单细胞droplet数据的特征，本期介绍sctransform的原理[1]，以及如何根据自己的数据选择合适的标准化方法。

由于磁珠与mRNA连接效率，反转录效率和测序深度的差异，即使类型和状态完全相同的细胞，也存在总reads数不相等的情况。所以我们不能直接用reads数作为基因表达量，需要进行标准化。标准化方法的众多，不同的选择可能造成差异较大的结果。

我们先用PBMC3k测试数据比较LogNormalize和SCTransform标准化后的聚类结果。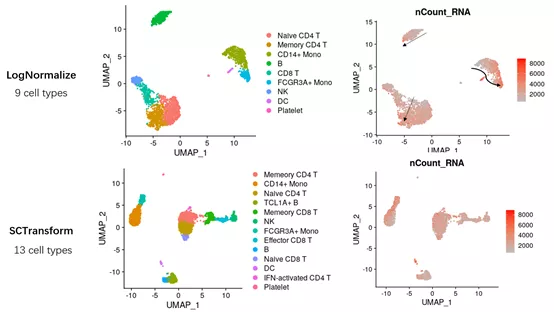

图1. 标准化方法LogNormalize和SCTransform的比较。
结果突出sctransform的两个优点：
1. 聚类结果受测序深度（nCount_RNA）影响较小；
2. 较高的细胞类型分辨率，鉴定到的细胞类型多。

单细胞转录组的标准化方法

单细胞转录组的标准化方法大概可以分成两大类。
一类是基于“size factors”的方法，除了上期提到的直接除以总数的log标准化，还有用spike-ins矫正的BASICS[2]，用多个“细胞池”衡量size factors的Scran[3]，还有传统用于bulk 转录组标准化的TMM和DESeq等[4,5]。

另一类是基于概率分布的方法，根据每个基因的表达量分布拟合特定的参数，然后对每个基因标准化，例如SCnorms，sctransform和scVI采用的ZINB等[6,7]。

这两大类标准化方法侧重的维度不同，size factors 侧重细胞维度；概率分布侧重基因维度。

图2. 单细胞标准化方法汇总
一个好的标准化方法应该包含以下特点[1]：
1. 标准化后的表达量不能与测序深度相关；
2. 一个基因标准化后的表达量方差不受数据的基因表达量和测序深度影响。

Log标准化方法并没有完全抵消测序深度的影响。有些数据用Log标准化，低表达量的基因与测序深度相关。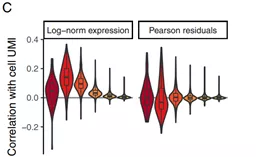

图3. sctransform文章 Figure3.C
另外，大部分基于size factor的方法都忽略了第二点，例如用Log标准化方法化后的数据，很多差异基因都集中在表达量较低的基因集里。说明差异基因的选择受0值的影响，集中在零表达较多的基因中（droplet数据低表达基因一般有较多的0值）。

图4. sctransform文章 Figure1.E 按照基因表达量从低到高划分6个组，计算每个组中基因在细胞间的差异。

所以有必要按照基因分组标准化。SCnorms虽然按照基因分组标准化，但它忽略了表达量为0的影响。Sctransform用模型拟合每个基因在不同细胞表达的分布，考虑了细胞间整体关系。

ZINB（zero-inflated negative binomial ）也是基于概率分布的方法，但它的前提假设已经收到不少学者的批判。ZINB的使用初衷是认为droplet数据存在技术性零值的情况，也就是我们常说的dropout。最近NBT杂志上有学者总结droplet数据的零值并不是技术原因造成的，而是生物本来的特征[8]。bayNorm的作者也认为没必要进行矫正[9]。这是直接打dropout插补软件的脸啊，哈哈哈。之前笔者在介绍Diffusion maps 的文章中，顺带介绍了Magic，它用线性代数的手段根据其他细胞的基因表达进行插补，可以认为是一种数据“smooth”手段。笔者认为这种处理有些画蛇添足。还有其他众多基于深度学习的零值填补工具也是。方法的使用需要在“原汁原味”和“过度修饰”之间寻找平衡。

Sctransform原理

Sctransform先拟合每个基因在不同细胞的reads数和测序深度的关系，然后矫正拟合结果，计算测序深度相关的reads数期望值和对应的方差，利用期望值和方差计算皮尔森残差，最后返回矫正后的reads数。

Sctransform的优点[1]：

1. 不根据size factor，也就是总的UMI数对每个细胞标准化；
2. 标准化方法建立在单细胞数据已知的关系之上：平均表达量和方差的关系。
3. 没有用log转化，z-scoring标准化（严格来说，sctransform还是有涉及的。计算皮尔森残差的公式很像z-score）
4. 综合来说，sctransform的标准化结果可以消除测序深度的影响。

接下来我们一步步探索sctransform标准化的过程。大概分为三步：
1. 负二项分布回归拟合每个基因的表达量和测序深度的关系；
2. Ksmooth矫正拟合结果；
3. 计算皮尔森残差，返回矫正reads数。

用sctranform 包可以直接得到Seurat::SCTranform的结果矩阵。

###sctranform package
library(sctransform)

pbmc_vst<-sctransform::vst(pbmc@assays$RNA@counts,return_cell_attr = TRUE)

umi_corrected <-sctransform::correct_counts(pbmc_vst, pbmc@assays$RNA@counts)

为了加强理解，我们用测试数据（PBMC3k）和基本的R函数，逐步实操，解读sctransform全过程。

第一步，用广义线性模型拟合每个基因的reads数和测序深度。上一期介绍了单细胞数据的基本特征，因为droplet的reads数服从指数型分布（泊松分布，负二项分布等），不服从正态分布，所以不用一般线性模型回归，需要用广义线性模型（generalize linear model，GLM）。拟合用R函数glm，方法选择quasi-possion，也是我们上期介绍的准泊松分布回归。这里也可以选择possion，我的测试结果差别不大。sctranform默认选择quasi-poisson。sctransform没有直接用负二项回归，可能是因为需要先估计参数θ。MASS包里有个函数glm.nb可以直接做负二项回归。拟合结果是每个基因的一对系数：beta0/beta1和负二项分布的参数θ。得到的θ值不小于1e-7。

负二项分布的参数θ可以根据方差和平均值的关系计算：方差=平均值+平均值^2 / θ。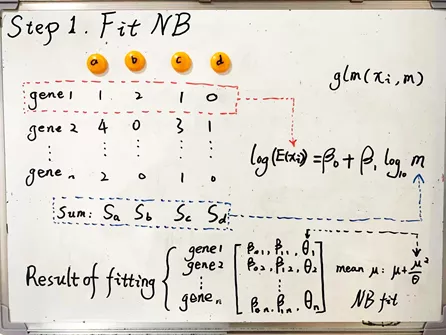

图5. sctransform标准化第一步
代码示例：

#####sctransform performed by basic function
####Step1. Fit independent regression models per gene.
#a.Get log10 total cell umi-count.
umi<- pbmc@assays$RNA@counts
log10_total_umi <- log10(apply(umi, 2, sum))
genes_cell_count <- apply(umi >= 0.01, 1, sum)
min_cells <- 5
genes <- rownames(umi)[genes_cell_count >= min_cells]
umi <- umi[genes, ]
#b.Fit regression per gene. This step is time consuming.
#The default method in Seurat::SCTransform is  quasipoisson.
message('Step1. Fit regression per gene.')
fitlist <- pbapply::pblapply(1:nrow(umi), function(x) {
  one_gene_umi <- umi[x,]
  df <- data.frame(x = one_gene_umi, y = log10_total_umi,stringsAsFactors = F)
  #fitquasi-poisson
  fit <- glm(x~y, family = quasipoisson, data = df)
  #estimate theta of the Negative Binomial Distribution
  theta <- as.numeric(x = MASS::theta.ml(y = one_gene_umi, mu =fit$fitted))
  c(theta, fit$coefficients)
})
fitmat <- do.call(rbind, fitlist)
colnames(fitmat) <- c('theta','coef1','coef2')
rownames(fitmat) <- rownames(umi)
min_theta <- 1e-7
fitmat[, 'theta'] <- pmax(fitmat[, 'theta'], min_theta)
head(fitmat)
#                   theta      coef1       coef2
#AL627309.1   0.17341591 -13.361622  2.27618038
#RP11-206L10.2 0.07424443 -33.732009  7.93363429
#LINC00115    0.34198012 -11.985290  2.07560184
#NOC2L        0.81967017  -9.432605  2.13505914
#KLHL17       0.14195506 -18.710149  3.80026829
#PLEKHN1      0.12861560  -5.739757 -0.05754689

第二步，对拟合结果进行矫正。有些低表达基因的0值比例较高，经常发生过度拟合的情况，产生和log标准化类似的偏差，即低表达基因会产生跟生物特征无关的差异。用smooth的方法分别所有基因的三个参数做回归曲线，得到矫正后的参数，克服过拟合的情况。在做回归之前，先剔除掉一些离群点（outliers），确保smooth的效果。

图6. sctransform标准化第二步
代码示例：

####Step2. Exploit the relationship of model parameter values and gene mean to learn global trends.
message('Step2.Exploit the relationship of model parameter values and gene mean to learn global trends.')
genes_log_gmean <- log10(exp(apply(log(umi+1),1,mean)) - 1)
dispersion_par <- log10(1 +10^genes_log_gmean / fitmat[, 'theta'])
model_pars <- fitmat[, colnames(fitmat) != 'theta']
model_pars <- cbind(dispersion_par, model_pars)
outliers <- apply(model_pars, 2,function(y) is_outlier(y, genes_log_gmean, th = smooth_th))
outliers <- apply(outliers, 1, any)
genes <- rownames(model_pars)
model_pars <- model_pars[!outliers, ]
genes_log_gmean_filtered <- genes_log_gmean[!outliers]
umi_filtered <- umi[!outliers,]
#c. Select bandwidth to be used for smoothing
bw<- bw.SJ(genes_log_gmean_filtered) * bw_adjust
#d. For parameter predictions
x_points <- pmax(genes_log_gmean, min(genes_log_gmean_filtered))
x_points <- pmin(x_points, max(genes_log_gmean_filtered))
#e. Take results from step 1 and fit/predict parameters to all genes
o<- order(x_points)
model_pars_fit <- matrix(NA_real_, length(genes), ncol(model_pars),
                           dimnames = list(genes,colnames(model_pars)))
#f. fit / regularize dispersion parameter
model_pars_fit[o, 'dispersion_par'] <- ksmooth(x =genes_log_gmean_filtered, y = model_pars[, 'dispersion_par'],
                                                x.points = x_points, bandwidth = bw, kernel='normal')$y
#g. global fit / regularization for all coefficients
for(i in 2:ncol(model_pars)) {
   model_pars_fit[o, i] <- ksmooth(x = genes_log_gmean_filtered, y =model_pars[, i],
                                    x.points =x_points, bandwidth = bw, kernel='normal')$y
}
#h. back-transform dispersion parameter to theta
theta <- 10^genes_log_gmean / (10^model_pars_fit[, 'dispersion_par']- 1)
model_pars_fit <- model_pars_fit[, colnames(model_pars_fit) !='dispersion_par']
model_pars_fit <- cbind(theta, model_pars_fit)
head(model_pars_fit)
#                   theta     coef1    coef2
#AL627309.1    0.16044310 -12.67683 2.052024
#RP11-206L10.2 0.09224051 -13.18194 2.034810
#LINC00115     0.27512873 -12.06563 2.091616
#NOC2L         0.59993304  -9.91381 2.276511
#KLHL17        0.14428703 -12.81262 2.055785
#PLEKHN1       0.12742043 -13.22216 2.130464

第三步，根据拟合矫正后的参数计算皮尔森残差，返回矫正后的reads矩阵。经过第二步可以得到每个基因的β0，β1和θ。接下来，根据β0，β1和测序深度m可以计算拟合后的平均表达量μ，根据μ和θ可以计算标准差σ，然后皮尔森残差由μ，σ和原始数据进行类似z-score的计算得出。皮尔森残差设定了最大值，不超过总细胞数的平方根。另外，最后的矫正矩阵并不是皮尔森残差Zij，而是根据拟合的参数和皮尔森残差，将所有细胞测序深度的中位数作为所有细胞的初始测序深度，再根据之前的公式换算得到矫正后的reads count矩阵Xij corrected。最后一点在sctransform文章中似乎没有提及。

图7. sctransform标准化第三步
代码示例：

####Step3. Use the regularized regressionparameters to define an affine function that
 #transforms UMI counts into Pearson residuals.
 message('Step3. Use the regularized regression parameters to define anaffine function that transforms UMI counts into Pearson residuals.')
 coefs <- model_pars_fit[, -1, drop=FALSE]
 theta <- model_pars_fit[, 1]
  #get pearson residuals
 regressor_data_orig <- cbind(rep(1,length(log10_total_umi)),log10_total_umi)
  mu<- exp(tcrossprod(coefs, regressor_data_orig))
 variance <- mu + mu^2 / theta
 pearson_residual <- (umi - mu) / sqrt(variance)
  #generate output
 regressor_data_median <- regressor_data_orig
 regressor_data_median[,'log10_total_umi'] <-apply(regressor_data_median[, 'log10_total_umi', drop=FALSE], 2, function(x)rep(median(x), length(x)))
  mu<- exp(tcrossprod(coefs, regressor_data_median))
 variance <- mu + mu^2 / theta
  y.res <- mu + pearson_residual *sqrt(variance)
 y.res <- round(y.res, 0)
 y.res[y.res < 0] <- 0
 correct_mat <- as(y.res,)
 umi_corrected_log1p <- as(log(correct_mat + 1),)

完整代码请到我的github上查看[10]。用R的基础函数实现sctransform的标准化过程，总共只需153行代码。

总结：

1. 单细胞标准化方法众多，大概分成两类：一是基于size factors的方法，一是基于基因分布回归的方法。
2. Sctransform标准化方法在pbmc数据的表现明显优于Lognormalize的方法。
3. Sctransform有多个参数可以调整。如拟合广义线性模型中的方法参数，sctransform默认选择quasi-possion，比较符合droplet单细胞数据的特点。第二个参数可以选择是否矫正过拟合（do_regularize）,另外还可以改变smooth过程的outliers数（th，th越大outliers越少，保留更多基因，但拟合可能会偏离）。笔者认为，对于大多数模型来说，拟合回归次数越多，最后得到的数据越失真。Sctransform做了两次拟合回归，一次是每个基因的广义线性回归，另一次是所有基因的参数回归。如何取舍，由实际情况而定。
4. 单细胞标准化方法的选择根据实际的数据情况而定。可以先看看自己数据平均值和方差是否符合负二项分布的特征。一般droplet数据，如10X的数据可以优先考虑sctransform。而全长数据，如SmartSeq的数据，不是sctransform的设计初衷，可以尝试用scran等基于size factors的方法。然后看看高变基因是否集中在低表达量的基因，如果偏差过于明显，可以尝试sctranform。
5. 如果不同方法的标准化结果差不多，那就用原理最简单的方法，比如LogNormalize。

下期预告：单细胞矩阵初步精简，高变基因（high variable genes）的选择

参考链接：
[1]. Hafemeister, Christoph, and Rahul Satija.”Normalization and variance stabilization of single-cell RNA-seq datausing regularized negative binomial regression.” Genome biology 20.1 (2019): 1-15.
[2]. Vallejos, Catalina A., John C. Marioni,and Sylvia Richardson. “BASiCS: Bayesian analysis of single-cellsequencing data.” PLoS Comput Biol 11.6 (2015): e1004333.
[3]. Lun, Aaron TL, Karsten Bach, and John C.Marioni. “Pooling across cells to normalize single-cell RNA sequencingdata with many zero counts.” Genome biology 17.1 (2016): 75.
[4]. Robinson, Mark D., and Alicia Oshlack.”A scaling normalization method for differential expression analysis ofRNA-seq data.” Genome biology 11.3 (2010): 1-9.
[5]. Anders, Simon, and Wolfgang Huber.”Differential expression analysis for sequence count data.” Nature Precedings (2010): 1-1.
[6]. Bacher, Rhonda, et al. “SCnorm:robust normalization of single-cell RNA-seq data.” Nature methods 14.6 (2017): 584.
[7]. Lopez, Romain, et al. “Deepgenerative modeling for single-cell transcriptomics.” Nature methods 15.12 (2018): 1053-1058.
[8]. Svensson V. Droplet scRNA-seq is not zero-inflated[J]. Nature Biotechnology, 2020, 38(2): 147-150.
[9]. Tang W, Bertaux F, Thomas P, et al. bayNorm: Bayesian gene expression recovery, imputation and normalization for single-cell RNA-sequencing data[J]. Bioinformatics, 2020, 36(4): 1174-1181.
[10]. https://github.com/Zhihao-Huang/SingleCellOmics/blob/master/base_sctransform.R