本文来自“单细胞组学”公众号 原文链接：https://mp.weixin.qq.com/s/ewHdefHB33-G-X3i6ex0-A

上期总结了单细胞常用的拟时序算法，本期主要介绍RNA velocity的应用、算法原理和核心代码实现。

内容概要：

  1. RNA velocity简介与示例
  2. RNA velocity算法原理
  3. RNA velocity核心代码实现
  4. 总结与展望

    RNA velocity能做什么？

    RNA velocity可以根据单细胞转录组数据，给每个细胞一个显示发展趋势的箭头。
    可以显示细胞短时间内的周期变化，如细胞周期[1]。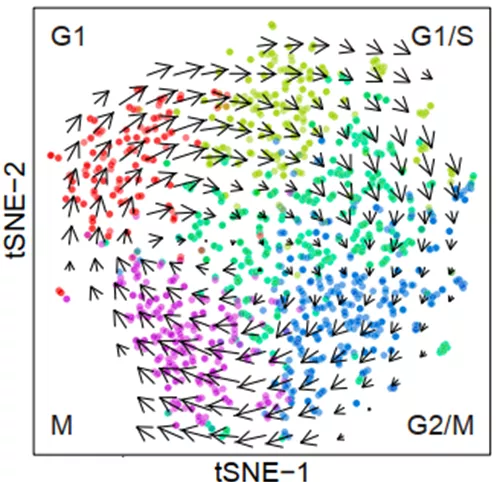
    RNA velocity, 预见未来 - 图1
    来自MERFISH文章Fig.4 [1]

也可以显示发育轨迹，如海马体单细胞的发育轨迹[2]。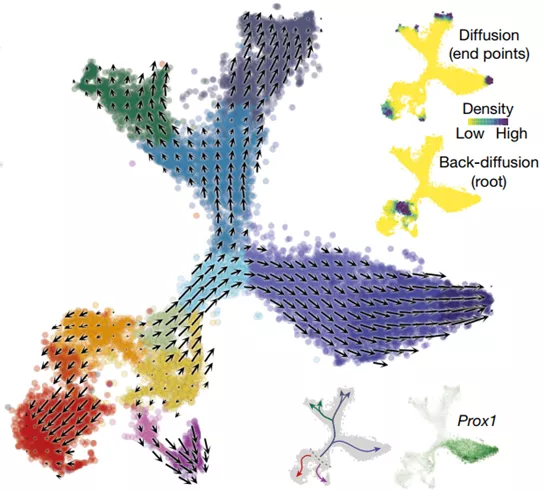
RNA velocity, 预见未来 - 图2
来自RNA velocity文章Fig.3[2]

RNA velocity与其他发育轨迹算法有何不同？

RNA velocity最直观的不同，是它的计算依据，包括两个对象：未剪切mRNA和已剪切mRNA。其他算法大多基于总的mRNA表达矩阵。

RNA velocity生物知识背景

影响单细胞成熟mRNA总量有三个主要的生物进程：

  • 转录
  • 剪切
  • 降解

RNA velocity, 预见未来 - 图3
由于每道工序的运行速率和转换效率存在差异，生物信号的调控，从转录信号发出，到蛋白生成，需要一定时间。这种系统性延迟，可以形成周期性震荡，这对生命体某些功能至关重要，如睡眠周期，心脏跳动的脉冲信号等。

我们用α，β，γ分别表示转录，剪切，降解这三个过程，用u和s分别表示未剪切mRNA的量和已剪切mRNA的量。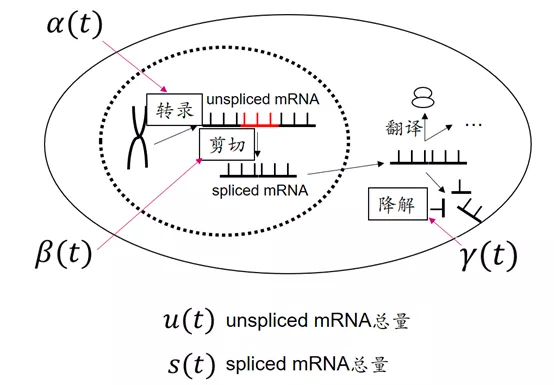
RNA velocity, 预见未来 - 图4

某个基因的调控过程，可以表现为：转录起始信号α发出，未剪切mRNA的量u逐渐增多，紧随着，已剪切mRNA的量s也开始逐渐增多，如下右图。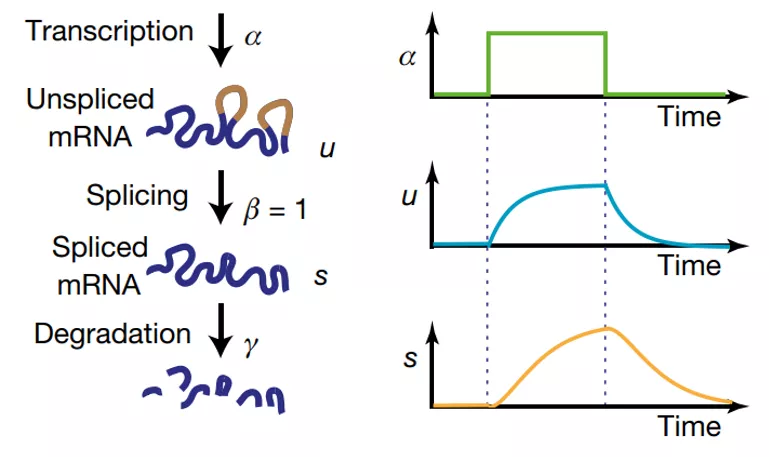
RNA velocity, 预见未来 - 图5

这种调控模式类似系统生物学中经典的前馈网络，共门I型前馈网络（ coherent type-1 feed-forwardloop, C1-FFL），如下图所示。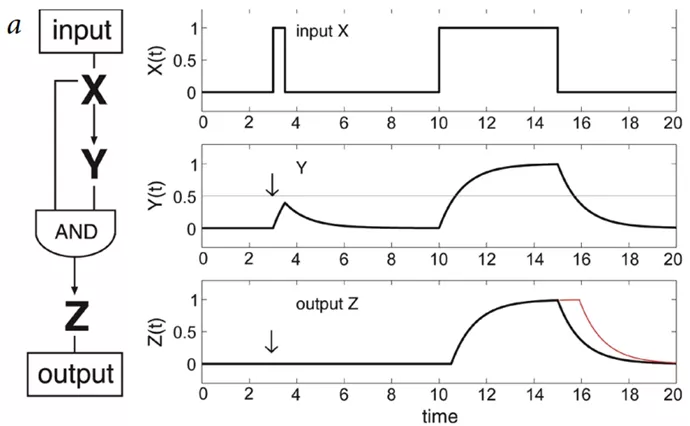
RNA velocity, 预见未来 - 图6
I型前馈网络+共门。Y基因只有达到一定阈值时，才能促发Z基因的表达。意义在于，过滤噪声刺激，降低敏感性[2]。

RNA velocity模型

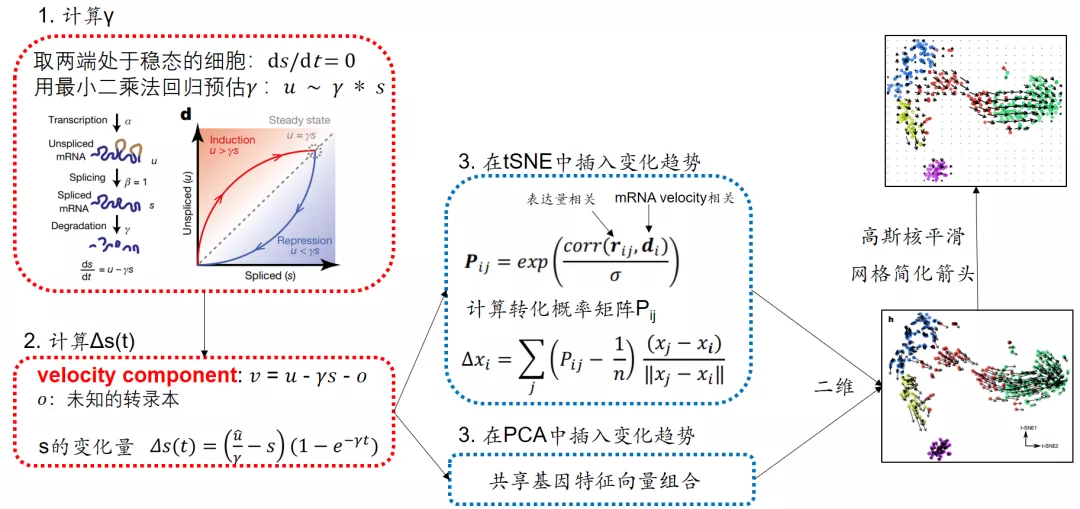
为了得到每个细胞的发展趋势，RNA velocity首先计算每个基因已剪切mRNA总量s的变化速率，然后算出未来某一时间t的已剪切mRNA总量s(t), 最后根据线性或者非线性的方法，将s(0)和s(t)插到二维图中，代表箭头的两端，表示每个细胞的发展趋势。

简要步骤：

  1. 计算每个基因的降解常数γ；
  2. 计算每个基因的s(t);
  3. 在PCA或者tSNE中可视化趋势。

    1. 预估降解常数γ

    根据上文提到的5个对象进行建模，未剪切mRNA的量u和已剪切mRNA的量s的变化速率可以表示为：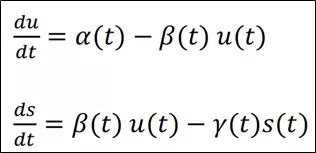
    RNA velocity, 预见未来 - 图7
    可以对模型进行简化。假设转录速率α不变，剪切效率完美，β=1，最终得到𝑢和γ*𝑠的关系：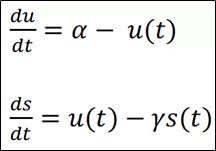
    RNA velocity, 预见未来 - 图8
    已剪切mRNA总量s的变化速率= 未剪切mRNA总量 u–降解系数γ x s
    根据scRNA-seq数据可以到u和s表达矩阵。在s稳定的条件下，即ds/dt= 0时，u = γs，我们就可以根据线性回归的方法，预估每个基因的γ值。

如何确定s恒定不变的条件呢？

下图用另一种方式展示上文的前馈网络：首先转录，纵坐标u逐渐增多，圆点开始往上升，随着剪切过程的进行，横坐标s也增多，圆点开始往右边移动。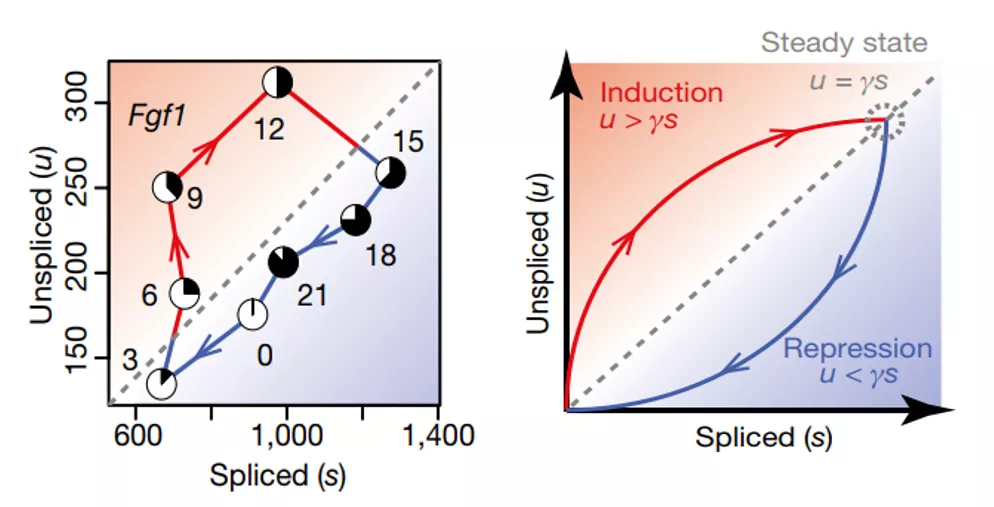
RNA velocity, 预见未来 - 图9
当已剪切mRNA总量s处于稳态时，生成s的量和降解s的量相等，u达到最大值，也就是上图右图虚线表示的区域。这是递增后的稳态。相反的，也存在递减后的稳态。
因此，满足s恒定条件的细胞，处于u取值区间的两端。我们可以根据这些满足条件的细胞，回归计算γ值。

2. 预估s(0)未来的变化趋势s(t)

求解上述的微分方程：
f80ec9626d872991f84606f60873e8d8.png0b503a8378ea2d3f8d49ace458054c72.png
最终得到：
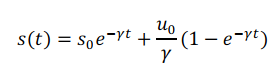
a085206ab0bbff90c51da513722c148e.pngimage.png
因此，根据时间=0时的三个数值：未剪切mRNA总量u0，已剪切mRNA总量s0，γ值，代入公式可以计算时间=t时的已剪切mRNA总量s(t)。

考虑并非所有的转录本都有注释，非剪切mRNA总量u里有部分是未知的，我们把这些干扰定义为o。通过s非0且u=0的细胞比例量化o。最终的s变化速率：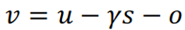
d7ae0455b4f71b9b653db8e56abfce14.png

经过o调整后的未剪切mRNA总量: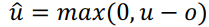
58ed7f4ea07f84baa92acdc1e38a6b2b.png

最后得到经过t时间s的变化量Δs(t) = s(t) – s0：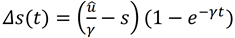
469d413b55dc0bbf81d755266ae418ac.pngimage.png

3. 在PCA中可视化

根据s0的基因特征向量组合，计算s(t)细胞特征向量组合。如果细胞过多，箭头过于密集，可以用高斯核平滑的方法，网格化箭头。

4. 在tSNE中可视化

非线性降维的插入比较复杂，首先根据一个细胞的表达量与其他细胞的RNA velocity向量的相关系数，经过指数核函数变换，得到转移概率矩阵P。
43b20dda332eacecb4e028ceba6d1909.pngimage.png
然后累加与其他细胞的P与cosine距离的相乘，得到箭头向量：
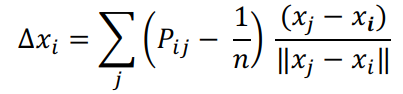
image.png468304aab4be31ebd18fa27d7f163534.png

核心代码实现
测试数据选取MERFISH的数据，来自MERFISH研究细胞周期的文章[1]。
1. 测试数据导入

  2. #load data
  3. emat <- read.table('emat.txt')
  4. nmat <- read.table('nmat.txt')
  5. comdf <- read.table('cell_cluster.txt', header = T)
  6. cell.colors <- comdf$color
  7. names(cell.colors) <- comdf$cellID
  1. 分别标准化矩阵s和u。
    参数解读：
    mult：测序深度，也就是标准化的scale factor； ```r

rvel.cd.unpooled <- list();

bring matrices to the same gene set (just in case)

vg <- intersect(rownames(emat),rownames(nmat)); emat <- emat[vg,]; nmat <- nmat[vg,] pcount <- 1;

size estimates

emat.size <- Matrix::colSums(emat) nmat.size <- Matrix::colSums(nmat) emat.cs <- emat.size[colnames(emat)]/mult; nmat.cs <- nmat.size[colnames(nmat)]/mult; emat.log.norm <- log(as.matrix(t(t(emat)/emat.cs))+pcount);

size-normalized counts

conv.emat.norm <- t(t(emat)/emat.cs) conv.nmat.norm <- t(t(nmat)/nmat.cs) rvel.cd.unpooled$conv.nmat.norm <- conv.nmat.norm; rvel.cd.unpooled$conv.emat.norm <- conv.emat.norm;

  1. 3. 回归计算γ值<br />参数解读：<br />fit.quantile：定义稳态细胞的两端表达区间的比例；根据数据而定，Smart-Seq 5%, droplet数据2%；<br />steady.state.cells：自定义稳态细胞；<br />deltaT、deltaT2：时间变化单位，默认为1.<br />min.nmat.emat.correlation：根据u和s表达量的相关系数过滤基因；<br />min.nmat.emat.slope：根据γ值过滤基因；
  2. ```r
  3. ko <- data.frame(do.call(rbind,parallel::mclapply(sn(rownames(conv.emat.norm)),function(gn) {
  4.     df <- data.frame(n=(conv.nmat.norm[gn,steady.state.cells]),
  5.                      e=(conv.emat.norm[gn,steady.state.cells]))
  6.     o <- 0;
  7.     zi <- df$e<1/emat.cs[steady.state.cells]; 
  8.     if(any(zi)) { o <- sum(df$n[zi])/(sum(zi)+1)} 
  9.     df$o <- o;
  10.     eq <- quantile(df$e,p=c(fit.quantile,1-fit.quantile))
  11.     pw <- as.numeric(df$e>=eq[2] | df$e<=eq[1])
  12.     d <- lm(n~e,data=df,weights=pw)
  13.     # note: re-estimating offset here
  14.     return(c(o=as.numeric(coef(d)[1]),g=as.numeric(coef(d)[2]),r=cor(df$e,df$n,method='spearman')))
  15.   },mc.cores=n.cores,mc.preschedule=T)))
  16. ko <- na.omit(ko)
  17. vi <- ko$r>min.nmat.emat.correlation
  18. ko <- ko[vi,]
  19. vi <- ko$g>min.nmat.emat.slope
  20. ko <- ko[vi,]
  1. 计算s(t)，即projected s。
    gamma <- ko$g; 
offset <- ko$o; 
names(gamma) <- names(offset) <- rownames(ko);
cat("calculating RNA velocity shift ... ")
deltaE <- t.get.projected.delta(conv.emat.norm,conv.nmat.norm,gamma,offset=offset,delta=deltaT)
rvel.cd.unpooled$gamma <- gamma;
# reduced cell normalization (only genes for which momentum was estimated)
emat.norm <- emat[rownames(emat) %in% rownames(deltaE),]
emat.sz <- emat.cs;
emat.norm <- t(t(emat.norm)/(emat.sz));
emn <- t.get.projected.cell2(emat.norm,emat.sz,as.matrix(deltaE),mult = mult,delta=deltaT2);
cat("done\n")
full.ko$valid <- rownames(full.ko) %in% rownames(ko)
rvel.cd.unpooled <- c(rvel.cd.unpooled,list(projected=emn,current=emat.norm,deltaE=deltaE,deltaT=deltaT,ko=full.ko,mult=mult,kCells=1));
  2. 在PCA中可视化趋势
    pca.velocity.plot.simplify(rvel.cd.unpooled,
               nPcs=2,
               plot.cols=1,
               cell.colors=cell.colors,
               pc.multipliers=c(1,-1) ## adjust as needed to orient pcs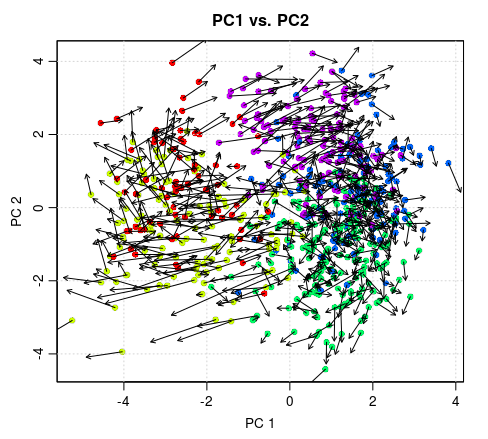
)
    ef29b156904b7c6e661abb27b57b05dc.png
    网格化
    pca.velocity.plot.simplify(rvel.cd.unpooled,
               nPcs=2,
               plot.cols=1,
               cell.colors=cell.colors,
               pc.multipliers=c(1,-1), ##adjust as needed to orient pcs
               show.grid.flow = TRUE,
               grid.n=20 ## adjust as needed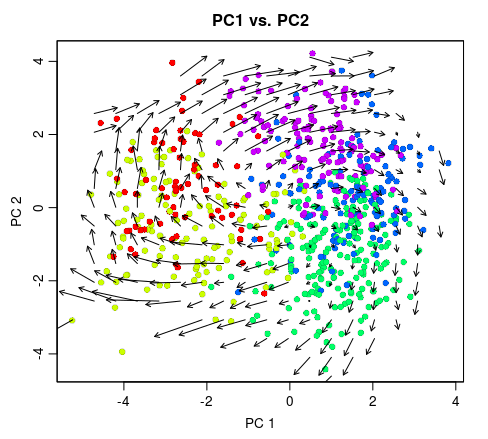
)
    904e8db0435370f4f6642569a15e29f6.png
    6. 显示细胞周期
    ###plot cell-cycle phase
library(Seurat)
library(ggplot2)
rownames(comdf) <- comdf$cellID
seus4 <- CreateSeuratObject(counts =emat, meta.data = comdf)
seus4 <- CellCycleScoring(object =seus4, g2m.features = cc.genes$g2m.genes,
                               s.features =cc.genes$s.genes)
#pca
x0 <- rvel.cd.unpooled$current
x1 <- rvel.cd.unpooled$projected
message("Step1. log ... ")
x0.log <- log2(x0 + 1)
x1.log <- log2(x1 + 1)
message("Step2. pca ... ")
cent <- rowMeans(x0.log)
epc <- pcaMethods::pca(t(x0.log - cent),center = F, nPcs = 2)
message("Step3. pc multipliers ...")
epc@loadings <- t(t(epc@loadings) *c(1,-1))
epc@scores <- scale(epc@completeObs,scale = F, center = T) %*% epc@loadings
head(epc@scores)
ccdf <- as.data.frame(epc@scores)
ccdf <- cbind(ccdf,seus4@meta.data[,c('S.Score','G2M.Score','Phase')])
ggplot(ccdf, aes(PC1, PC2, color = Phase))+ geom_point() + theme_bw()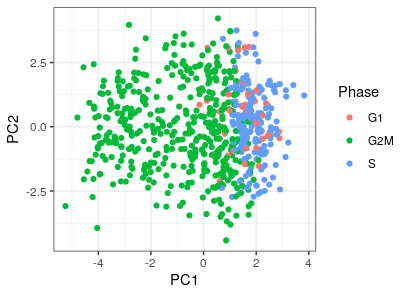
    f6bee61b85214c404466a21a8bda0fef.pngimage.png
    显示细胞周期S和G2M的分数
    ggplot(ccdf, aes(PC1, PC2, color =S.Score)) + geom_point() + theme_bw() +
scale_color_gradientn(colours = c('grey','yellow','red'))
ggplot(ccdf, aes(PC1, PC2, color =G2M.Score)) + geom_point() + theme_bw() +
scale_color_gradientn(colours = c('grey','yellow','red'))
    RNA velocity, 预见未来 - 图26
    详细源码和示例数据可以查看github链接：
    https://github.com/Zhihao-Huang/SingleCellOmics/blob/master/000.RNA_velocity_simplify.R

    总结与展望

  3. RNA velocity原理可以分为两大部分：Δs(t)计算和可视化。总结为下图。
    RNA velocity, 预见未来 - 图27
    2. RNA velocity最大的不足之处是稳态细胞的定义。2020年新出scVelo用新的算法弥补这一缺陷[4]。

  4. 举一反三，将RNA velocity推广至单细胞多组学，如“蛋白质 velocity”[5]。
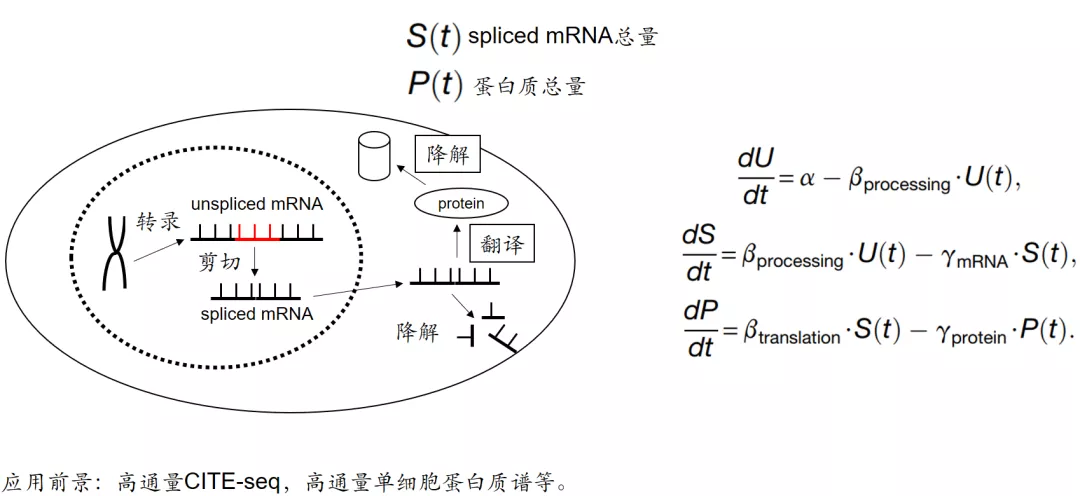
    RNA velocity, 预见未来 - 图28
    “ATAC velocity” 类似的思路也有人探索，如Share-seq这一类可以检测同一个细胞的染色体开放区域和转录组的技术[6]。

  5. 随着单细胞多组学技术逐渐完善，迫切需要寻找不同组学之间的共同规律，使之成为共同体。RNA velocity这一类的分子动力学模型，将是多组学分析的有力工具之一。

参考链接：
[1] Xia C, Fan J, Emanuel G, et al. Spatial transcriptomeprofiling by MERFISH reveals subcellular RNA compartmentalization and cellcycle-dependent gene expression[J]. Proceedings of the National Academy of Sciences, 2019, 116(39): 19490-19499.
[2] La Manno G, Soldatov R, Zeisel A, et al. RNA velocity ofsingle cells[J]. Nature, 2018, 560(7719): 494-498.
[3] Shen-Orr S S, Milo R, Mangan S, et al.Network motifs in the transcriptional regulation network of Escherichiacoli[J]. Nature genetics, 2002, 31(1): 64-68.
[4] Bergen V, Lange M, Peidli S, et al. Generalizing RNA velocity to transient cell states through dynamical modeling[J]. Nature biotechnology, 2020, 38(12): 1408-1414.
[5] Gorin G, Svensson V, Pachter L. Protein velocity and acceleration from single-cell multiomics experiments[J]. Genome biology, 2020, 21(1): 1-6.
[6] Clyde D. SHARE-seq reveals chromatin potential[J]. Nature Reviews Genetics, 2020: 1-1.