二叉树遍历

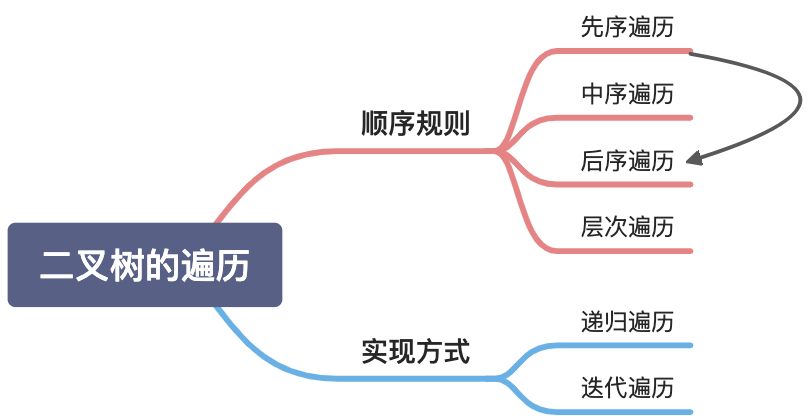
深度优先遍历

前序遍历

根 —> 左 —> 右

• 递归：

  var preorderTraversal = function(root) {
        let result = []
    // 定义递归函数
    const preorderfun = (root)=>{
            if(!root) return // 递归中止条件
        // 前序遍历顺序：根-左-右
        result.push(root.val)
        preorderfun(root.left)
          preorderfun(root.right)
    }
    preorderfun(root)
    return result;
  }

• 迭代：辅助队列

  var preorderTraversal = function(root) {
    let result = [];
  if(!root) return result;
  let stack = []; // 声明一个辅助栈，出栈的时候将左右节点入栈
  stack.push(root);
  while(stack.length){
      let cur = stack.pop();
    result.push(cur.val);
    // 先将右节点入栈，方便后弹出
    if(cur.rigth){
            stack.push(cur.right);
    }
    if(cur.left){
            stack.push(cur.left);
    }
  }
  return result;
  }

  中序遍历

  左 —> 根 —> 右

• 递归：

  var inorderTraversal = function(root) {
         let result = []
    const inorderFun = (root)=>{
            if(!root) return;
          inorderFun(root.left);
          result.push(root.val);
          inorderFun(root.right);
    }
    return result;
  }

• 迭代：辅助栈 当前root作为游标 ```javascript var inorderTraversal = function(root) {

    let result = []

  if(!root) return;

  let stack = [];
  let cur = root;
  while(cur || stack.length){
        while(cur){
            stack.push(cur.left);
          cur = cur.left
    }
      cur = stack.pop();
      result.push(cur.val);
      cur = cur.right;

  }

  return result;

  }

<a name="u5lpG"></a>
#### [后序遍历](https://leetcode-cn.com/problems/binary-tree-postorder-traversal/comments/)
> 左 --> 右 --> 根
- **递归：**
```javascript
var postorderTraversal = function(root) {
    let result = [];
  const postorderFun = (root)=>{
          if(!root) return;
        postorderFun(root.left);
      postorderFun(root.right);
      result.push(root.val);
  }
  return result;
}

• 迭代：辅助队列

  var postorderTraversal = function(root) {
  // 定义结果数组
    let result = [];
  // 处理边界条件
  if(!root) return;
  // 初始化栈结构
  let stack = [];
  // 首先将根结点入栈
  stack.push(root);
  // 若栈不为空，则重复出栈、入栈操作
  while(stack.length){
    // 将栈顶结点记为当前结点
      let cur = stack.pop();
    // 当前结点就是当前子树的根结点，把这个结点放在结果数组的头部
    result.unshift(cur.val);
    // 若当前子树根结点有左孩子，则将左孩子入栈
    if(cur.left){
        stack.push(cur.left)
    }
    // 若当前子树根结点有右孩子，则将右孩子入栈
    if(cur.right){
        stack.push(cur.right)
    }
  }
  // 返回结果数组
  return result;
  }

  广度优先遍历

  层序遍历