点击查看【music163】

前言

不知道大家的项目中有没有涉及到浮点数的计算，Java 提供的浮点类型 float 和 double 都存在计算精度的问题。本文参考网上一些资料，尝试分析浮点类型的底层逻辑，并且给出浮点数计算的一些使用案例。

关于浮点数底层原理涉及到计算机的一些底层知识，所以内容较多，占了较大的篇幅，如果对这块不感兴趣，可以直接看结论，参考我提供的浮点数计算的工具类。

版本约定

我们先来看两个例子，第一个例子是判断两个浮点数是否相等，代码如下所示：

  1. public static void main(String[] args) {
  2.     float f1 = 1.6f + 0.3f;
  3.     float f2 = 1.9f;
  4.     if (f1 == f2) {
  5.         System.out.println("1.6 + 0.3 等于 1.9");
  6.     } else {
  7.         System.out.println("1.6 + 0.3 不等于 1.9");
  8.     }
  9. }

运行程序，输出：

  1. 1.6 + 0.3 不等于 1.9

我们看到 1.6 + 0.3 竟然不等于 1.9，和我们设想的不一样，直接通过 == 来比较浮点数是不可靠的。

第二个例子我们来打印一下刚才的两个浮点数。

  1. public static void main(String[] args) {
  2.     float f1 = 1.6f + 0.3f;
  3.     float f2 = 1.9f;
  4.     System.out.println("1.6 + 0.3 = " + f1);
  5.     System.out.println("1.9 = " + f2);
  6. }

运行程序，输出：

  1. 1.6 + 0.3 = 1.9000001
  2. 1.9 = 1.9

所以上面的比较才会输出不相等，原来 1.6 + 0.3 后的值是 1.9000001，很明显相加后的数值精度发生了改变。

接下来，我们来分析，为什么 Java 的浮点类型存在精度的问题？

浮点数底层原理

在分析浮点数的底层原理之前，我们先看思考一下浮点数的定义是什么，为什么在计算机中它叫浮点数？

什么是浮点数？

首先，我们需要理解什么是浮点数？

之前我们学习了定点数，其中「定点」指的是约定小数点位置固定不变。那浮点数的「浮点」就是指，其小数点的位置是可以是漂浮不定的。

关于定点数的文章参考这篇：计算机系统基础（三）定点数

这怎么理解呢？

其实，浮点数是采用科学计数法的方式来表示的，例如十进制小数 8.345，用科学计数法表示，可以有多种方式：

  1. 8.345 = 8.345 * 10^0
  2. 8.345 = 83.45 * 10^-1
  3. 8.345 = 834.5 * 10^-2
  4. ...

看到了吗？用这种科学计数法的方式表示小数时，小数点的位置就变得「漂浮不定」了，这就是相对于定点数，浮点数名字的由来。

使用同样的规则，对于二进制数，我们也可以用科学计数法表示，也就是说把基数 10 换成 2 即可。

到这里我们已经知道什么是浮点数了，接下来了解小数是如何在计算机中存储的？

浮点数如何表示数字？

我们已经知道，浮点数是采用科学计数法来表示一个数字的，它的格式可以写成这样：

  1. V = (-1)^S * M * R^E

其中各个变量的含义如下：

  • S：符号位，取值 0 或 1，决定一个数字的符号，0 表示正，1 表示负；
  • M：尾数，用小数表示，例如前面所看到的 8.345 * 10^0，8.345 就是尾数；
  • R：基数，表示十进制数 R 就是 10，表示二进制数 R 就是 2；
  • E：指数，用整数表示，例如前面看到的 10^-1，-1 即是指数。

如果我们要在计算机中，用浮点数表示一个数字，只需要确认这几个变量即可。

假设现在我们用 32 bit（float 类型就是 32 bit 的） 表示一个浮点数，把以上变量按照一定规则，填充到这些 bit 上就可以了：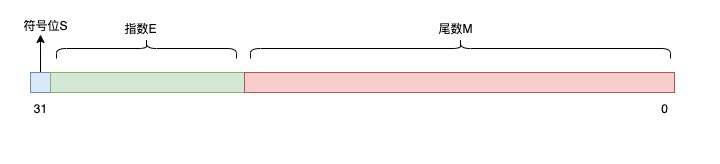
大数值与浮点数计算 - 图1
假设我们定义如下规则来填充这些 bit：

  • 符号位 S 占 1 bit
  • 指数 E 占 10 bit
  • 尾数 M 占 21 bit

按照这个规则，将十进制数 25.125 转换为浮点数，转换过程就是这样的（D 代表十进制，B 代表二进制）：

Tips：二进制的小数点和十进制的小数点是不同的，二进制小数点后是 2 的负幂，十进制是 10 的负幂。

  • 25.125 的整数部分：25(D) = 11001(B)；
  • 小数部分：0.125(D) = 1 / 8 = 2^-3 = 0.001(B)；
  • 所以，25.125 的二进制形式就是 11001.001；
  • 转换成二进制科学计数法：25.125(D) = 11001.001(B) = 1.1001001 * 2^4(B)。

所以符号位 S = 0，尾数 M = 1.001001(B)，指数 E = 4(D) = 100(B)。

按照上面定义的规则，填充到 32 bit 上，就是这样：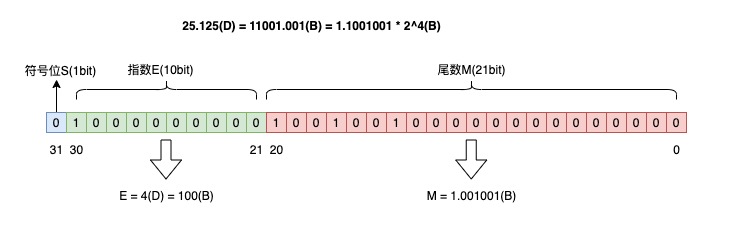
大数值与浮点数计算 - 图2
浮点数的结果就出来了，是不是很简单？

但这里有个问题，我们刚才定义的规则，符号位 S 占 1 bit，指数位 E 占 10 bit，尾数 M 占 21 bit，这个规则是我们拍脑袋随便定义出来的。

如果你也想定一个新规则，例如符号位 S 占 1 bit，指数位 E 这次占 5 bit，尾数 M 占 25 bit，是否也可以？当然可以。

按这个规则来，那浮点数表示出来就是这样：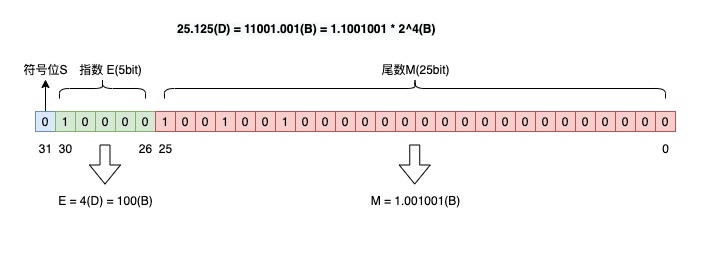
大数值与浮点数计算 - 图3
我们可以看到，指数和尾数分配的位数不同，会产生以下情况：

  1. 指数位越多，尾数位则越少，其表示的范围越大，但精度就会变差，反之，指数位越少，尾数位则越多，表示的范围越小，但精度就会变好；
  2. 一个数字的浮点数格式，会因为定义的规则不同，得到的结果也不同，表示的范围和精度也有差异。

早期人们提出浮点数定义时，就是这样的情况，当时有很多计算机厂商，例如 IBM、微软等，每个计算机厂商会定义自己的浮点数规则，不同厂商对同一个数表示出的浮点数是不一样的。

这就会导致，一个程序在不同厂商下的计算机中做浮点数运算时，需要先转换成这个厂商规定的浮点数格式，才能再计算，这也必然加重了计算的成本。

那怎么解决这个问题呢？业界迫切需要一个统一的浮点数标准。

浮点数标准

直到 1985 年，IEEE 组织推出了浮点数标准，就是我们经常听到的 IEEE754 浮点数标准，这个标准统一了浮点数的表示形式，并提供了 2 种浮点格式：

  • 单精度浮点数 float：32 位，符号位 S 占 1 bit，指数 E 占 8 bit，尾数 M 占 23 bit；
  • 双精度浮点数 double：64 位，符号位 S 占 1 bit，指数 E 占 11 bit，尾数 M 占 52 bit。

为了使其表示的数字范围、精度最大化，浮点数标准还对指数和尾数进行了规定：

  1. 尾数 M 的第一位总是 1（因为 1 <= M < 2），因此这个 1 可以省略不写，它是个隐藏位，这样单精度 23 位尾数可以表示了 24 位有效数字，双精度 52 位尾数可以表示 53 位有效数字；
  2. 指数 E 是个无符号整数，表示 float 时，一共占 8 bit，所以它的取值范围为 0 ~ 255。但因为指数可以是负的，所以规定在存入 E 时在它原本的值加上一个中间数 127，这样 E 的取值范围为 -127 ~ 128。表示 double 时，一共占 11 bit，存入 E 时加上中间数 1023，这样取值范围为 -1023 ~ 1024。

除了规定尾数和指数位，还做了以下规定：

  • 指数 E 非全 0 且非全 1：规约形式的浮点数，按上面的规则正常计算，这个指数的范围是 -126 ~ 127；
  • 指数 E 全 0，尾数非 0：非规约形式的浮点数，尾数隐藏位不再是 1，而是 0(M = 0.xxxxx)，这样可以表示 0 和很小的数
  • 指数 E 全 1，尾数全 0：特殊值，正无穷大/负无穷大（正负取决于 S 符号位）
  • 指数 E 全 1，尾数非 0：特殊值，NaN(Not a Number)

大数值与浮点数计算 - 图4
关于指数的无符号表示和取值范围，我们再深入讲解一下。

指数是如何实现无符号表示的？

指数可能是负数，也有可能是正数，即指数是有符号整数，而有符号整数的计算是比无符号整数麻烦的。所以为了减少不必要的麻烦，在实际存储指数的时候，需要把指数转换成无符号整数。那么怎么转换呢？

单精度浮点数的指数部分占 8 bit，为了消除负数带来的实际计算上的影响（比如比较大小，加减法等），可以在实际存储的时候，给指数做一个简单的映射，加上一个偏移量，比如 float 的指数偏移量为 127，这样就不会有负数出现了。

比如下面的计算，都加了 127 的偏移量：

  • 指数如果是 6，则实际存储的是 6 + 127 = 133，即把 133 转换为二进制之后再存储；
  • 指数如果是 -3，则实际存储的是 -3 + 127 = 124，即把 124 转换为二进制之后再存储；
  • 当我们需要计算实际代表的十进制数的时候，再把指数减去偏移量即可。

    指数的取值范围是多少？

其实，按照规则正常计算的指数范围是 -126 ~ 127，即属于所谓的规约形式的浮点数。为什么需要这样规定呢？

主要是因为全 0 和 全 1 的只指数都被用在了非规约形式的浮点数和特殊值上，上面也写到了，比如表示 0 和很小的数、正无穷大、负无穷大、NaN。

标准浮点数的表示

有了这个统一的浮点数标准，我们再把 25.125 转换为标准的 float 浮点数：

  • 25.125 的整数部分：25(D) = 11001(B)；
  • 小数部分：0.125(D) = 1 / 8 = 2^-3 = 0.001(B)；
  • 所以，25.125 的二进制形式就是 11001.001；
  • 转换成二进制科学计数法：25.125(D) = 11001.001(B) = 1.1001001 * 2^4(B)。

所以 S = 0，尾数 M = 1.001001 = 001001（去掉 1，隐藏位），指数 E = 4 + 127（中间数） = 135(D) = 10000111(B)。填充到 32 bit 中，如下：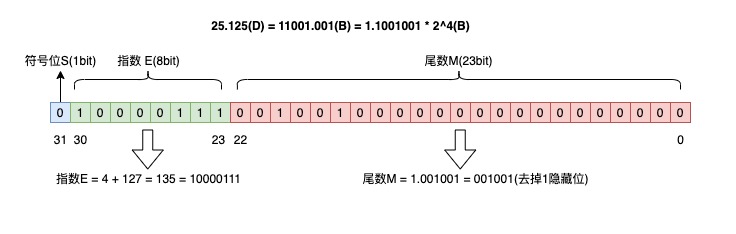
大数值与浮点数计算 - 图5
这就是标准 32 位浮点数的结果。

如果用 double 表示，和这个规则类似，指数位 E 用 11 bit 填充，尾数位 M 用 52 bit 填充即可。

浮点数为什么有精度损失？

我们再来看一下，平时经常听到的浮点数会有精度损失的情况是怎么回事？

如果我们现在想用浮点数表示 0.2，它的结果会是多少呢？

0.2 转换为二进制数的过程为，不断乘以 2，直到不存在小数为止，在这个计算过程中，得到的整数部分从上到下排列就是二进制的结果。

  1. 0.2 * 2 = 0.4 -> 0
  2. 0.4 * 2 = 0.8 -> 0
  3. 0.8 * 2 = 1.6 -> 1
  4. 0.6 * 2 = 1.2 -> 1
  5. 0.2 * 2 = 0.4 -> 0（发生循环）
  6. ...

所以 0.2(D) = 0.00110…(B)。

因为十进制的 0.2 无法精确转换成二进制小数，而计算机在表示一个数字时，宽度是有限的，无限循环的小数存储在计算机时，只能被截断，所以就会导致小数精度发生损失的情况。

浮点数的范围和精度有多大？

最后，我们再来看一下，用浮点数表示一个数字，其范围和精度能有多大？

以单精度浮点数 float 为例，它能表示的最大二进制数为 +1.1.11111…1 2^127（小数点后 23 个 1），而二进制 1.11111…1 ≈ 2，所以 float 能表示的最大数为 2^128 = 3.4 10^38，即 float 的表示范围为：-3.4 10^38 ~ 3.4 10 ^38。

它能表示的精度有多小呢？

float 能表示的最小二进制数为 0.0000….1（小数点后 22 个 0，1 个 1），用十进制数表示就是 1/2^23。

用同样的方法可以算出，double 能表示的最大二进制数为 +1.111…111（小数点后 52 个 1） 2^1023 ≈ 2^1024 = 1.79 10^308，所以 double 能表示范围为：-1.79 10^308 ~ +1.79 10^308。

double 的最小精度为：0.0000…1(51 个 0，1 个 1)，用十进制表示就是 1/2^52。

从这里可以看出，虽然浮点数的范围和精度也有限，但其范围和精度都已非常之大，所以在计算机中，对于小数的表示我们通常会使用浮点数来存储。

浮点数计算

通过上面浮点数的底层原理分析，我们知道浮点数存在精度问题，所以在 Java 浮点数类型的使用过程中，要注意文章开头例举的案例，特别是金融类型的业务，需要提供精度相对比较高的计算，我们需要用到 Java 中提供的大数值：BigInteger 和 BigDecimal 这两个类。

关于这两个类的使用，这里提供一个工具类，大家可以参考，有特殊需求的，根据自己的业务需求添加相应的功能。

  1. import java.math.BigDecimal;
  3. /**
  4.  * 算术工具类
  5.  */
  6. public class ArithmeticUtils {
  8.     // 默认除法运算精度
  9.     private static final int DEF_DIV_SCALE = 6;
  11.     /**
  12.      * 提供精确的加法运算。
  13.      * 
  14.      * @param v1 被加数
  15.      * @param v2 加数
  16.      * @return 两个参数的和
  17.      */
  18.     public static double add(double v1, double v2) {
  19.         BigDecimal b1 = new BigDecimal(Double.toString(v1));
  20.         BigDecimal b2 = new BigDecimal(Double.toString(v2));
  21.         return b1.add(b2).doubleValue();
  22.     }
  24.     /**
  25.      * 提供精确的減法运算。
  26.      * 
  27.      * @param v1 被减数
  28.      * @param v2 减数
  29.      * @return 两个参数的差
  30.      */
  31.     public static double sub(double v1, double v2) {
  32.         BigDecimal b1 = new BigDecimal(Double.toString(v1));
  33.         BigDecimal b2 = new BigDecimal(Double.toString(v2));
  34.         return b1.subtract(b2).doubleValue();
  35.     }
  37.     /**
  38.      * 提供精确的乘法运算。
  39.      * 
  40.      * @param v1 被乘数
  41.      * @param v2 乘数
  42.      * @return 两个参数的积
  43.      */
  44.     public static double mul(double v1, double v2) {
  45.         BigDecimal b1 = new BigDecimal(Double.toString(v1));
  46.         BigDecimal b2 = new BigDecimal(Double.toString(v2));
  47.         return b1.multiply(b2).doubleValue();
  48.     }
  50.     /**
  51.      * 提供相对精确的除法运算，使用默认精度。
  52.      * 
  53.      * @param v1 被除数
  54.      * @param v2 除数
  55.      * @return 两个参数的商
  56.      */
  57.     public static double div(double v1, double v2) {
  58.         return div(v1, v2, DEF_DIV_SCALE);
  59.     }
  61.     /**
  62.      * 提供相对精确的除法运算。当发生除不尽的情况时，由scale参数指 定精度，以后的数字四舍五入。
  63.      * 
  64.      * @param v1 被除数
  65.      * @param v2 除数
  66.      * @param scale 精度
  67.      * @return 两个参数的商
  68.      */
  69.     public static double div(double v1, double v2, int scale) {
  70.         if (scale < 0) {
  71.             throw new IllegalArgumentException("精度（scale）必须大于等于0");
  72.         }
  73.         if (v2 == 0) {
  74.             return 0;
  75.         }
  76.         BigDecimal b1 = new BigDecimal(Double.toString(v1));
  77.         BigDecimal b2 = new BigDecimal(Double.toString(v2));
  78.         return b1.divide(b2, scale, BigDecimal.ROUND_HALF_UP).doubleValue();
  79.     }
  81.     /**
  82.      * 提供四舍五入运算
  83.      * 
  84.      * @param v 被四舍五入数
  85.      * @param scale 精度
  86.      * @return 四舍五入之后的数
  87.      */
  88.     public static double round(double v, int scale) {
  89.         if (scale < 0) {
  90.             throw new IllegalArgumentException("精度（scale）必须大于等于0");
  91.         }
  92.         BigDecimal b = new BigDecimal(Double.toString(v));
  93.         BigDecimal one = new BigDecimal("1");
  94.         return b.divide(one, scale, BigDecimal.ROUND_HALF_UP).doubleValue();
  95.     }
  96. }

结论

关于浮点数计算这块，总结如下：

  1. 因为浮点数存在精度问题，不建议直接比较大小；
  2. 同样的，也不建议直接做算数计算；
  3. 浮点数的大小比较、算数计算可以使用大数值 BigDecimal 代替；

    转载

作者：殷建卫 链接：https://www.yuque.com/yinjianwei/vyrvkf/oktg7w 来源：殷建卫 - 架构笔记 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。