一步生成的扩散模型：Consistency Models - 知乎

今天在推特上看到了 consistency models 代码的开源

这篇工作的论文在今年3月放出，那时候还没有开源代码，但是其展现的潜力让人印象深刻。因为 Diffusion Models 在生成一张图片时需要多次进行模型推理，对于实时性较强的应用，就很难让人满意了。虽然也有后续一些采样相关的工作比如 DDIM，DPM-Solver，Uni-PC 将推理步数缩减到10步左右，但是还没有像这篇文章所claim的一步采样即能达到较好的效果。

笔者和大家一起来看看这篇文章。

Arxiv: https://arxiv.org/pdf/2303.01469.pdf

Code: https://github.com/openai/consistency_models

背景：Diffusion Models 的 SDE 形式和 ODE 形式

首先回顾一下diffusion的算法原理，假设我们有数据分布 pdata(x)p_{data}(x) , 扩散模型通过如下的 SDE 对数据分布进行

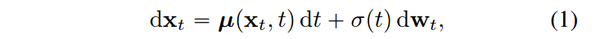
stochastic differential equation

songyang 推导出，上述 SDE 存在一个 ODE 形式的解轨迹

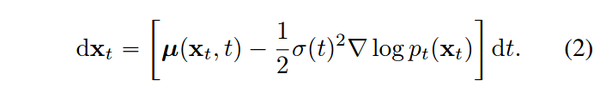
ODE trajectory

其中 \nabla \log p_t(x) 是 p_t(x) 的得分函数。得分函数是diffusion model 的直接或者间接学习目标。

采用 EDM 中的 setting，设置 \mu (x, t) = 0 , \sigma(t) = \sqrt{2t} , 训练一个得分模型 s_ {\phi}(x, t) \approx \nabla \log p_t(x)

上述 ODE 转为

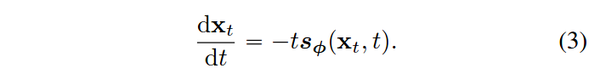
得到 ode 的具体形式后，利用现有的数值 ODE solver，如 Euler, Heun, Lms 等，即可解出 x(.). 考虑到数值精确性，我们往往不会直接求出原图即 x(0) ，而是计算出一个 x(t-\delta_t) ，持续这个过程来求出 x(0) 。

Consistency Models 的概念

回顾一下 diffusion 的采样过程，从先验分布 (x_{t_N}, t_N) 出发，推导采样过程

(x{t_N}, t_N) \rightarrow (x{t{N-1}}, t{N-1})\rightarrow … \rightarrow (x_{t_0}, t_0)

Consistency Models 假设存在一个函数 f ，对于上述过程中的每个点，f都能输出一个相同的值

即

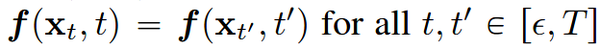
并且对于轨迹的起点 x_0 = \epsilon ，我们有

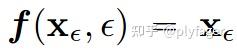
那么对于轨迹中任意一点，我们代入先验分布, 即可得到 f(xT, T) = x{\epsilon} 。这样也就完成了一步采样。

自然想到训练一个神经网络来拟合 f，但是这里要满足两个条件，一个是轨迹上的点输出值一致，一个是在起始时间点 f 为一个对于x的恒等函数。

作者做了如下的设计，巧妙的实现了上述目标

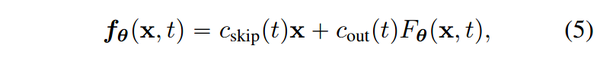
其中 c{skip} 和 c{out}为可微函数，满足 c{skip}(\epsilon) = 1, c{out}(\epsilon) = 0. F_{\theta} 为深度神经网络，输出维度同 x .

这样，第二个条件自然满足，因为有

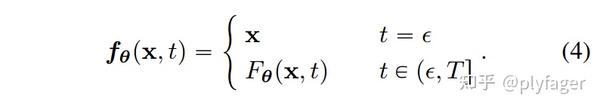
F_{\theta} 可使用一致性损失来学习。

观察 f 的性质，显然， f(xT, T) = x{\epsilon} 可以得到我们想要的生成结果。但一般认为，这样的生成误差会比较大。就像 DDPM 也可以通过预测噪声直接从 xt 预测 x_0 , 但我们会依赖 x_t, x_0 预测 x{t-1} ,依次向下采样来获得 x_0 来减小误差。

同样的，我们每次从 x{\tau_n} 预测出初始的 x 后，回退一步来预测 x{\tau_{n-1}} 来减小误差。因此有如下多步采样的算法。

Consistency Models 的训练方式

考虑到 Consistency Models 的性质，对采样轨迹上的不同点，f应该有一个相同的输出，自然我们需要找到采样的轨迹。

如果我们有预训练的diffusion model，自然可以构建轨迹。

假设采样轨迹的时间序列为

\epsilon = t_1<t_2<…<t_N = T

ODE sampler 的采样可以 formulate 成

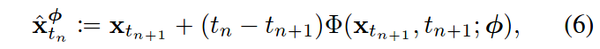
其中 \Phi( x{t{n+1}}, t_{n+1}; \phi) 为 ODE solver。

使用 Euler Solver, 代入求解对象式(3)，上式转为

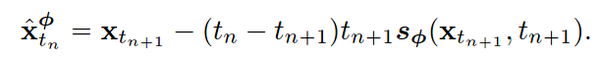
当然也可以采用其他的 Solver，一般来说阶数越高的 Solver 求解精度越高。

对于处于同一轨道的 (x{t{n+1}}, t{n+1}), (\hat{x}^{\phi}{t{n}}, t{n}) ，f应该有相同的输出，我们用距离函数 d 来衡量输出是否相同。

因而有如下训练损失

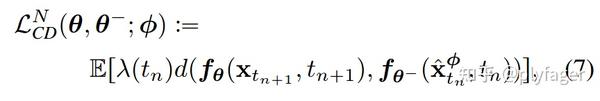
其中 \lambda 用来对不同时间步赋予不同重要性， \theta^{-} 为 EMA 版本的权重。

综合上述过程，蒸馏（Consistency Distillation）的算法为

在蒸馏的过程中，我们实际上用预训练模型来估计得分 \nabla \log p_t(x) 。 如果从头训练，需要找一个不依赖于预训练模型的估计方法。

作者在论文中证明了一种新得分函数的估计

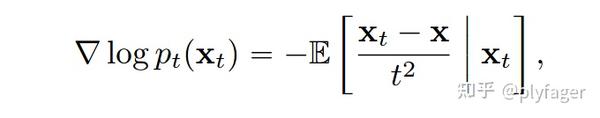
利用该得分估计，作者为从 Isolation Training 构建了一个新的训练损失，

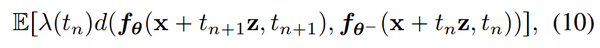
并且证明了该 Loss 和 Distillation Loss 在最大间隔趋于0时相等。即

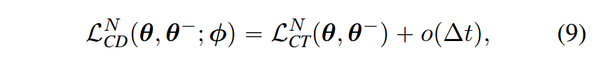
从而可以利用上述 loss 训练一个 Consistency Models，并且不依赖于已有 Diffusion Model。具体算法如下

实验结果

作者分析了总时间步 N ，EMA decay rate \mu 随时间轮次变化的Scheduler，以及 ODE solver, 距离函数 d 的选取对结果的影响，这里不做介绍。不过有意思的是，实验结果表明，使用 lpips 距离的效果会超出 l_1, l_2 函数，并且这种选取也会提升对比的蒸馏方法 Progressive Distillization 的效果。

这让我想起了两篇论文，Projected GANs Converge Faster 和 The Role of ImageNet Classes in Fréchet Inception Distance, 笔者认为使用 lpips 作为距离函数某种程度 hack 了 FID，从而取得了更好的指标。当 NFE = 1 时，这种效应尤其明显.

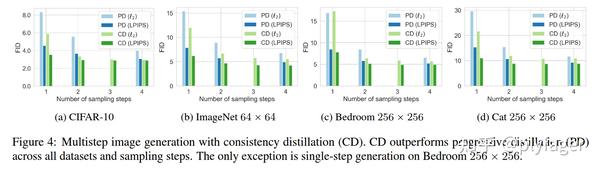
笔者简单看了一眼实验结果，CD(consistency distillatio)和 Diffusion 的其他蒸馏工作相比，该方法在1，2步采样下，结果是最好的，但似乎仍然无法与当前最好的GAN方法相比。CT (consistency distillation)点数则相差比较大，在 ImageNet 上 NFE =1 的 fid 甚至超过了 10。

但笔者仍认为该方法具有很高的价值，目前的diffusion models，采样速度确实是一个痛点，而现在有大量基于diffusion的工作，如果能把现有工作如 stable diffusion 用该方法进行蒸馏，有助于满足高实时性的需求。