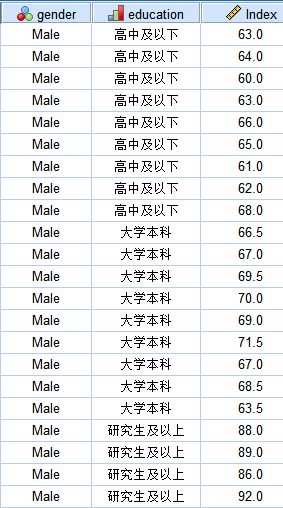
1.研究目的

两因素方差分析是研究在已知一个自变量（A）对因变量（C）的影响的情况下，判断另一个自变量（B）对这一相关关系是否存在作用

2.数据形式要求

3.需要满足的假设

1. 因变量为连续变量（观察）
2. 存在两个自变量，且自变量为分类变量（观察）
3. 各组间和组内的观测值相互独立（观察）
4. 任意分类中没有明显异常值（需要检验）
5. 任意分类中残差接近正态分布（需要检验）
6. 任意分类中的方差齐（需要检验）

   任意分类是两个因素交叉后的最小分类

4.对于假设的检验方式

4.1 对于组内异常值的检验

1. 尤其对于小样本，异常值的影响极为明显；

2. 一般对于异常值的定性研究用箱线图即可；

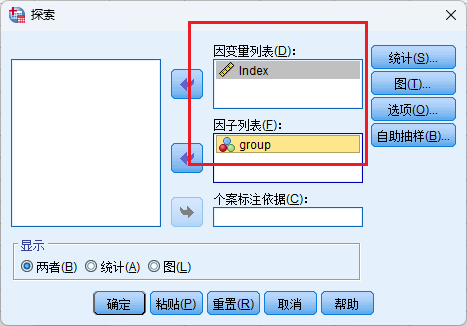
   分析-描述统计-探索

   

   箱线图结果的阅读

   

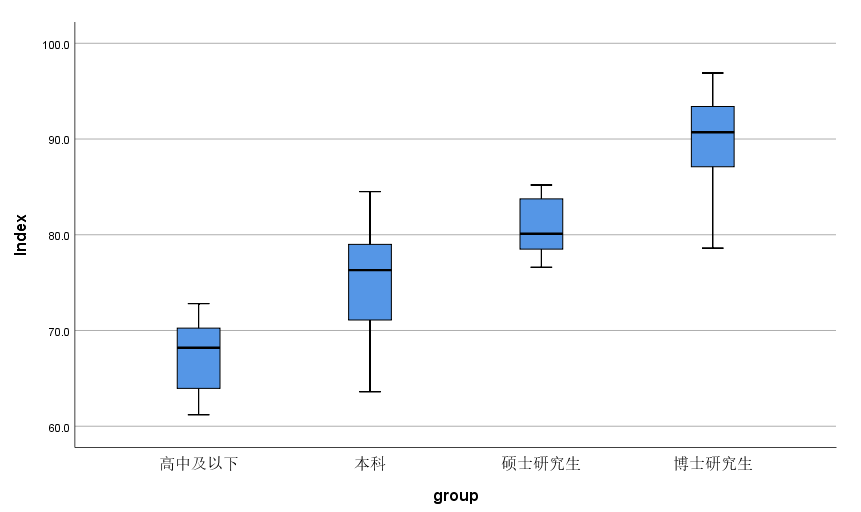
3. 从箱线图结果中未有发现标记点，可说明各组内没有明显的异常值；

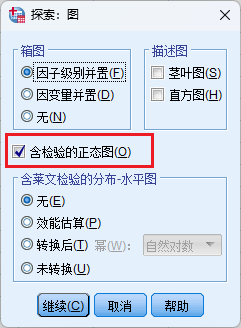
   4.2 各组的正态性检验

4. 正态性检验的操作方式和异常值操作一致；

5. 定量正态性检验一般用Shapiro-Wilk Test，定性检验可以采用PP图，QQ图，甚至直接绘制概率分布表等方式；

正态性检验结果的阅读

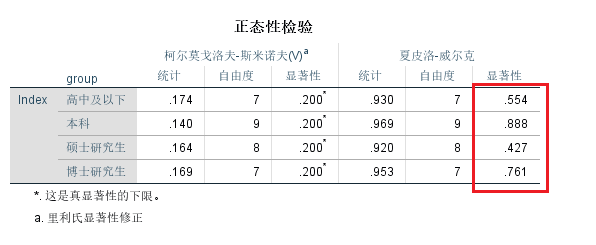
1. 从Shapiro-Wilk Test结果看，各组检验结果接受H0；

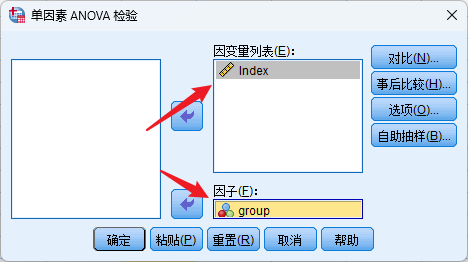
   5.操作方法

   分析-比较均值-单因素ANOVA Test

   

   选项按钮

   

2. 其中welch也可以进行勾选，welch主要是在方差不齐的时候，用其结果替代F检验结果

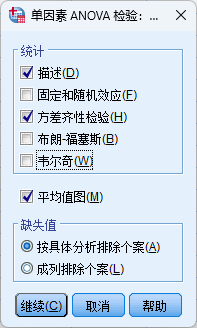
   事后两两比较按钮

3. 一般方差齐性的情况下事后两两比较采用S-N-K法和Tukey法。方差不齐的情况下，采用Games-Howell法

6.结果及解释

6.1 描述统计结果

描述性结果

方差齐性结果

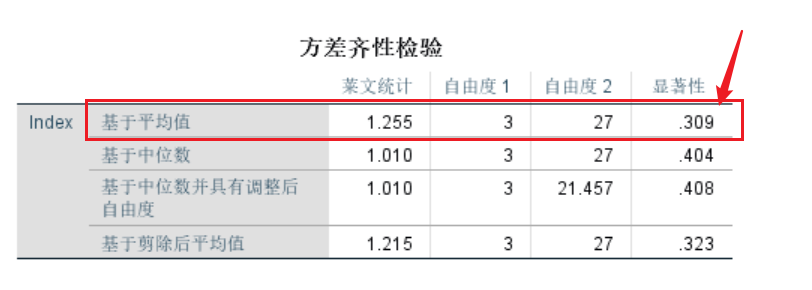:::info

1. 方差齐性检验H0：各组之间符合方差齐性 :::

2. 本案例中所有组之间具有方差齐性，可以进行但因素ANOVA检验

   6.2 ANOVA检验结果