1.检验目的

多个独立样本之间中位数差异性的非参数检验

本案例中为工作年限working_time和工作压力stress_score之间的区别

2.数据形式要求

与独立样本T检验格式一致
image.png

3.假设条件

  1. 有一个因变量，且因变量为连续变量或有序分类变量（观察）
  2. 存在多个分组（≥2个）（观察）

  3. 具有相互独立的观测值（观察）

    4.操作方式

    查看各组之间的分布情况

    查看各组的中位数情况

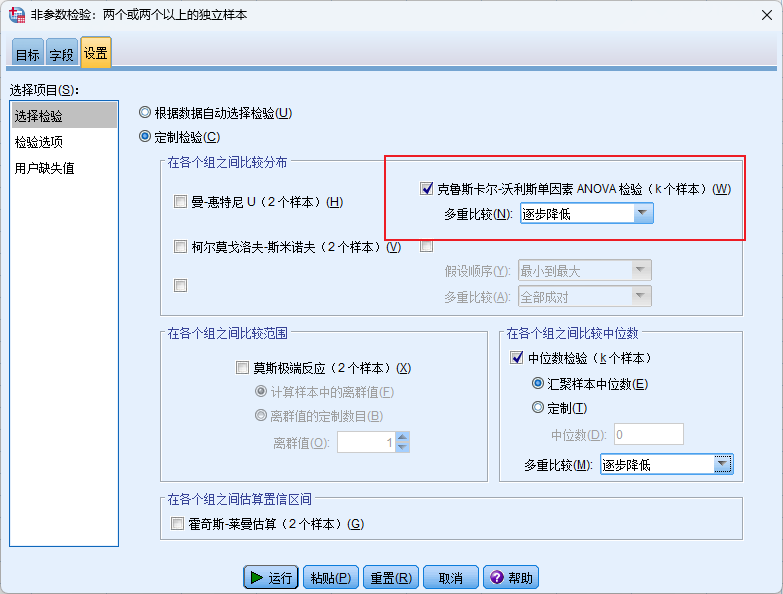
    进行Kruskal-Wallis H检验

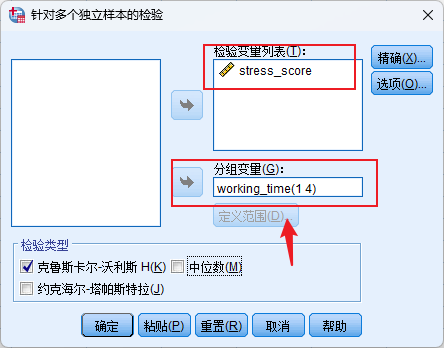
    方法一：分析-非参数检验-独立样本

    image.png
    image.png

    方法二：分析-非参数检验-旧对话框-k个独立样本

    特别注意：一般不用旧对话框进行检验，主要原因为其中无法显示两两比较结果
    image.png

    5.结果及解释

    5.1 样本的描述

    image.png

    5.2 Kruskal-Wallis H检验结果

    image.png :::info

  4. Kruskal-Wallis H检验H0：各组之间的中位数完全相同。 :::

  5. 基于以上结果，可以认为各组中位数不全相同，差异具有统计学意义（H= 21.989，P<0.001）。

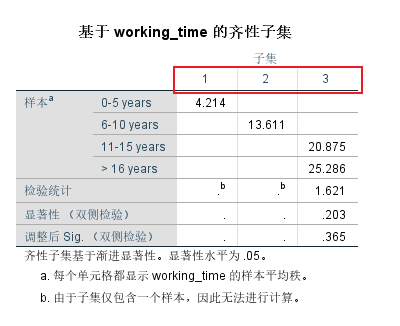
    5.3 两两比较寻找同质亚组的子集

    由于Kruskal-Wallis H检验拒绝了原假设，故要进行两两比较
    image.png

    5.4 结论

  6. 用Bonferroni法校正显著性水平的事后两两比较发现，CWWS评分的分布在工作年限0-5年和11-15年（调整后P=0.002）、0-5年和>16年（调整后P<0.001）的差异有统计学意义，其它组之间的差异无统计学意义；

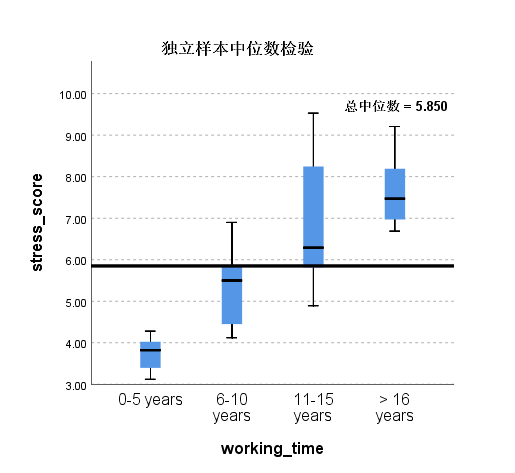
    各组CWWS评分的分布形状基本一致时

    比较不同工作年限人群之间CWWS评分的分布差异，采用Kruskal-Wallis H检验。根据直方图判断各组中CWWS评分分布的形状基本一致。各组CWWS评分的分布不全相同，差异具有统计学意义（H= 21.989，P<0.001）。工作0-5年CWWS评分中位数为3.82（n=7），6-10年CWWS评分中位数为5.50（n=9），11-15年CWWS评分中位数为6.29（n=8），>16年CWWS评分中位数为7.47（n=7），总的CWWS评分中位数为5.85（n=31）。采用Bonferroni法校正显著性水平的事后两两比较发现，CWWS评分的分布在工作年限0-5年和11-15年（调整后P=0.002）、0-5年和>16年（调整后P<0.001）的差异有统计学意义，其它组之间的差异无统计学意义。

    各组CWWS评分的分布形状不一致时

    比较不同工作年限人群之间CWWS评分的分布差异，采用Kruskal-Wallis H检验。根据直方图判断各组中CWWS评分分布的形状不一致。各组CWWS评分的分布不全相同，差异具有统计学意义（H= 21.989，P<0.001）。工作0-5年CWWS评分平均秩次为4.21（n=7），6-10年CWWS评分平均秩次为13.61（n=9），11-15年CWWS评分平均秩次为20.88（n=8），>16年CWWS评分平均秩次为25.29（n=7）。采用Bonferroni法校正显著性水平的事后两两比较发现，CWWS评分的分布在工作年限0-5年和11-15年（调整后P=0.002）、0-5年和>16年（调整后P<0.001）的差异有统计学意义，其它组之间的差异无统计学意义。