1.研究目的

单因素ANOVA本质用于比较多组数据之间的平均值差异

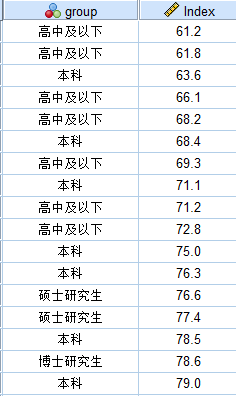
2.数据形式要求

类似T检验的数据要求
image.png

3.需要满足的假设

  1. 因变量为连续变量（观察）
  2. 有一个包含3个及以上分类、且组别间相互独立的自变量（观察）
  3. 各组间和组内的观测值相互独立（观察）
  4. 各组内没有明显异常值（需要检验）
  5. 各组内因变量符合正态分布（需要检验）

  6. 各组间的方差齐（需要检验）

    4.对于假设的检验方式

    4.1 对于组内异常值的检验

  7. 尤其对于小样本，异常值的影响极为明显；

  8. 一般对于异常值的定性研究用箱线图即可；

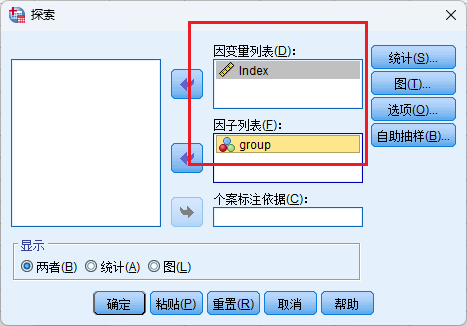
    分析-描述统计-探索

    image.png

    箱线图结果的阅读

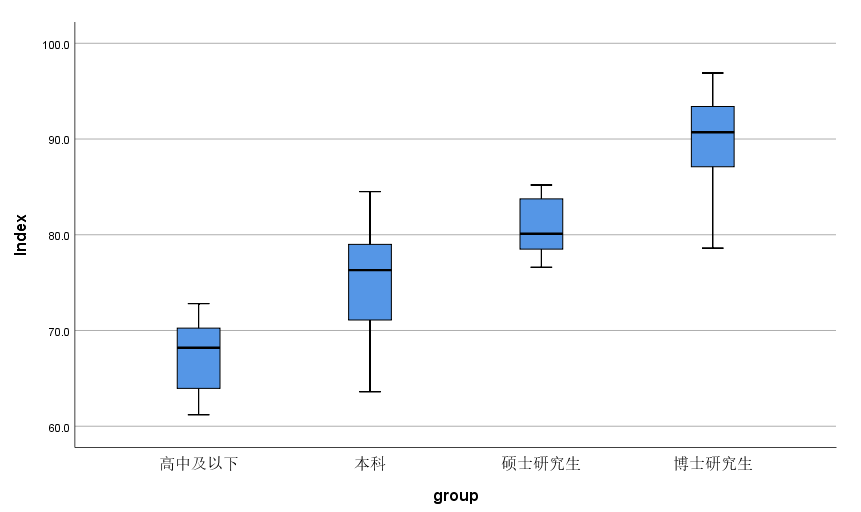
    image.png

  9. 从箱线图结果中未有发现标记点，可说明各组内没有明显的异常值；

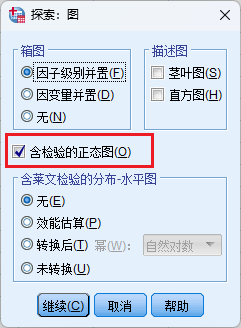
    4.2 各组的正态性检验

  10. 正态性检验的操作方式和异常值操作一致；

  11. 定量正态性检验一般用Shapiro-Wilk Test，定性检验可以采用PP图，QQ图，甚至直接绘制概率分布表等方式；

image.png

正态性检验结果的阅读

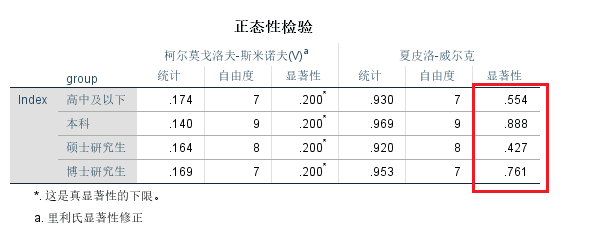
image.png

  1. 从Shapiro-Wilk Test结果看，各组检验结果接受H0；

    5.操作方法

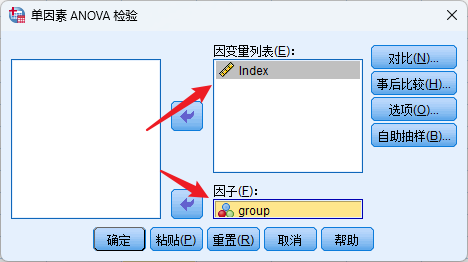
    分析-比较均值-单因素ANOVA Test

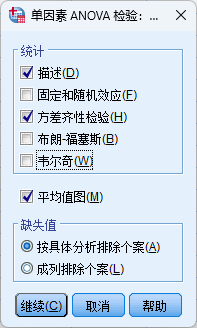
    image.png

    选项按钮

    image.png

  2. 其中welch也可以进行勾选，welch主要是在方差不齐的时候，用其结果替代F检验结果

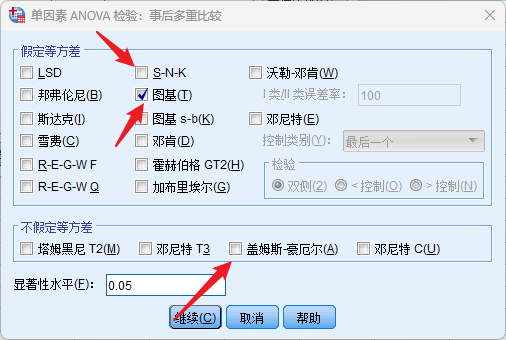
    事后两两比较按钮

  3. 一般方差齐性的情况下事后两两比较采用S-N-K法和Tukey法。方差不齐的情况下，采用Games-Howell法

image.png

6.结果及解释

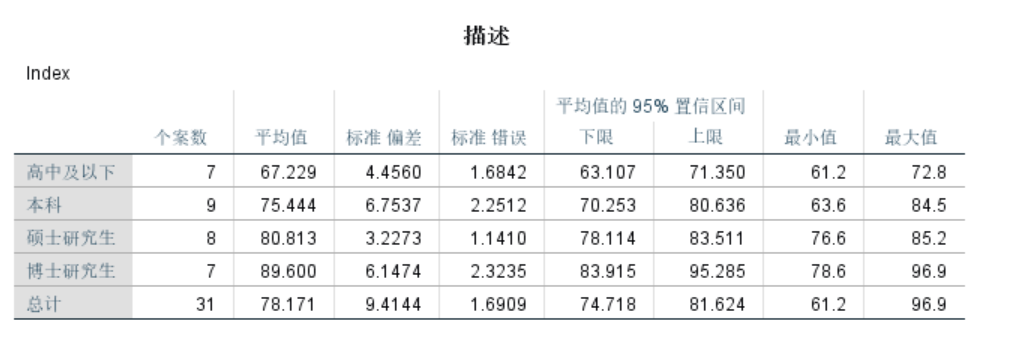
6.1 描述统计结果

描述性结果

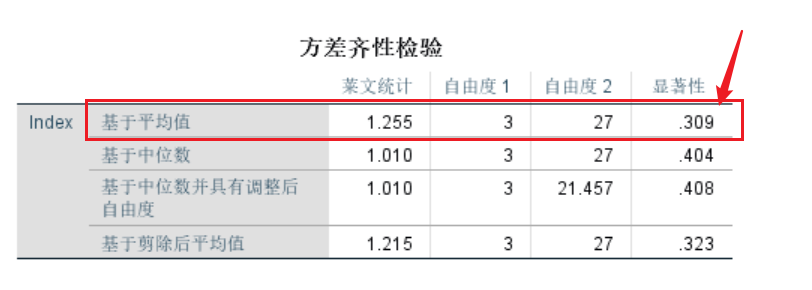
image.png

方差齐性结果

image.png :::info

  1. 方差齐性检验H0：各组之间符合方差齐性 :::

  2. 本案例中所有组之间具有方差齐性，可以进行但因素ANOVA检验

    6.2 ANOVA检验结果

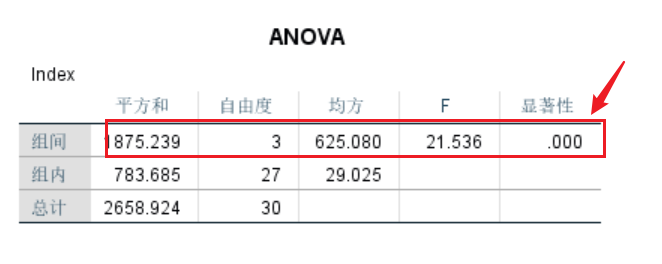
    image.png

  3. 从单因素方差检验结果看，差异具有统计学意义（P<0.05）。表示各组的均数不全相等（至少有一组均数不同于另一组）

    6.3 两两比较结果

    :::info

  4. 各组之间方差齐时

    1. 两两比较中一般使用LSD和S-N-K法；
    2. 如果事前没有对特定组间差异进行假设，或者关心所有组间的两两比较，则可以进行所有组间的两两比较。当满足方差齐性的条件时，可以使用Tukey检验进行组间两两比较；
    3. 当各组例数不相等时，Tukey检验不太适用。而应该使用校正后的Tukey-Kramer检验。Tukey-Kramer检验结果偏保守；
    4. spss中如果选择Tukey检验且各组案例数不相等时，系统默认输出结果为Tukey-Kramer检验结果

  5. 各组之间方差不齐时

    1. 方差不齐时必须使用校正的单因素方差分析；
    2. 一般可采用Welch法方差分析；
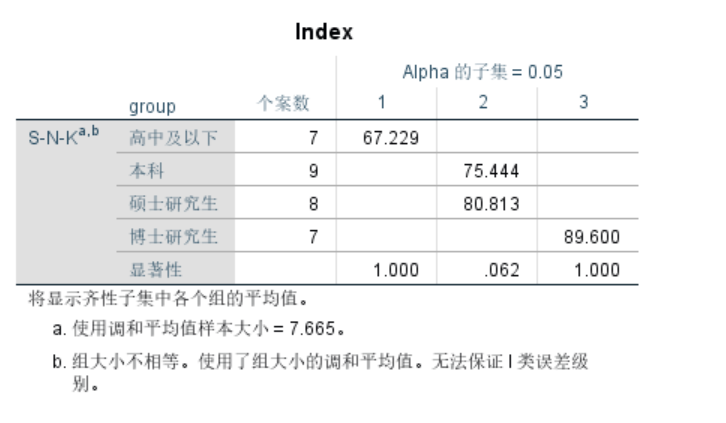
    3. 如果关心所有组间的两两比较时，推荐采用Games-Howell检验。Games-Howell检验不仅提供了每两个组间比较的P值，也给出了均数差值的置信区间。 ::: image.png

  6. 本案例中高中及以下及博士研究生组与其他组之间有显著性差异；

  7. 本科组与硕士研究生组之间无显著差异。

    6.4 结论

    方差齐，方差分析显示组间差异有统计学意义，并进行了两两比较

    采用单因素方差分析法，判断不同学历水平组间的幸福指数Index是否有差异。研究对象被分为4组：高中及以下组（7人）、本科生组（9人）、硕士研究生组（8人）、博士研究生组（7人）。经箱线图判断，数据无异常值；经Shapiro-Wilk检验，各组数据服从正态分布（P>0.05）；经Levene’s方差齐性检验，各组数据方差齐（P =0.309）。不同学历水平组间的幸福指数得分差异具有统计学意义，F=21.536，P <0.001。数据以均数±标准差的形式表示，幸福指数Index得分分别为：高中及以下组（67.23±4.46）、本科生组（75.44±6.75）、硕士研究生组（80.81±3.23）、博士研究生组（89.60±6.15）。Tukey检验结果表明，从高中及以下组到本科生组，Index平均得分增加8.22（95%CI：0.79~15.65），差异具有统计学意义（P=0.026）；从高中及以下组到硕士研究生组，Index平均得分增加13.58（95%CI：5.95~21.21），差异具有统计学意义（P <0.001），其他组比较解释同上。

    方差不齐，方差分析显示组间差异有统计学意义，并进行了两两比较。

    采用Welch方差分析法，判断不同学历水平组间的幸福指数Index是否有差异。研究对象被分为4组：高中及以下组（7人）、本科生组（9人）、硕士研究生组（8人）、博士研究生组（7人）。经箱线图判断，数据无异常值；经Shapiro-Wilk检验，各组数据服从正态分布（P>0.05）；假设经Levene’s方差齐性检验，各组数据方差不齐。不同学历水平组间的幸福指数得分差异具有统计学意义，Welch F=22.292，P<0.001。数据以均数±标准差的形式表示，幸福指数Index得分分别为：高中及以下组（67.23±4.46）、本科生组（75.44±6.75）、硕士研究生组（80.81±3.23）、博士研究生组（89.60±6.15）。Games-Howell检验结果表明，从高中及以下组到本科生组，Index平均得分增加8.22（95%CI：0.02~16.41），差异具有统计学意义（P=0.049）；从高中及以下组到硕士研究生组，Index平均得分增加13.58（95%CI：7.45~19.72），差异具有统计学意义（P <0.001），其他组比较解释同上。

    方差齐，方差分析显示组间差异无统计学意义。

    采用单因素方差分析法，判断不同学历水平组间的幸福指数Index是否有差异。研究对象被分为4组：高中及以下组（7人）、本科生组（9人）、硕士研究生组（8人）、博士研究生组（7人）。经箱线图判断，数据无异常值；经Shapiro-Wilk检验，各组数据服从正态分布（P>0.05）；经Levene’s方差齐性检验，各组数据方差齐（P =0.309）。数据以均数±标准差的形式表示，幸福指数Index得分分别为：高中及以下组（67.23±4.46）、本科生组（75.44±6.75）、硕士研究生组（80.81±3.23）、博士研究生组（89.60±6.15）。不同学历水平组间的幸福指数Index得分差异无统计学意义，F=1.116，P=0.523。

    方差不齐，方差分析显示组间差异无统计学意义。

    采用Welch方差分析法，判断不同学历水平组间的幸福指数Index是否有差异。研究对象被分为4组：高中及以下组（7人）、本科生组（9人）、硕士研究生组（8人）、博士研究生组（7人）。经箱线图判断，数据无异常值；经Shapiro-Wilk检验，各组数据服从正态分布（P>0.05）；经Levene’s方差齐性检验，各组数据方差不齐（P=0.002）。数据以均数±标准差的形式表示，数据以均数±标准差的形式表示，幸福指数Index得分分别为：高中及以下组（67.23±4.46）、本科生组（75.44±6.75）、硕士研究生组（80.81±3.23）、博士研究生组（89.60±6.15）。不同学历水平组间的幸福指数Index得分差异无统计学意义，Welch F=1.316，P=0.523。