1.检验目的

  1. 判断对于同一样本进行多段处理所获取的配对数据，来判断处理是否有效。仅用于两分类数据。

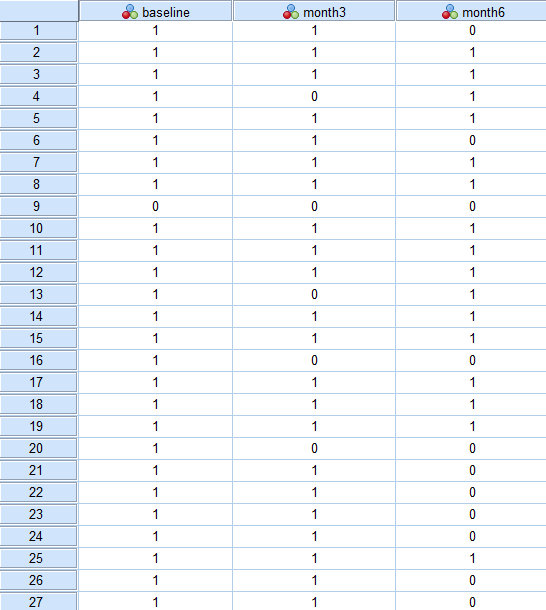
    案例随机选取了63例进行行为干预的研究对象，并收集了所有研究对象基线（baseline），干预3个月（month3）和干预6个月（month6）的吸烟状态。吸烟赋值为1，不吸烟赋值为0。

2.数据形式要求

不同的处理位于不同的字段
image.png

3.假设条件

  1. 观测变量为二分类，且两类之间互斥；（观察）
  2. 分组变量包含3个及以上分类，且各组之间相关（当分组变量只有2个分类时，可使用McNemar’s检验）；（观察）
  3. 随机样本；（观察）

  4. 样本量足够大；（需要检验）

    1. 当样本量n≥4且nk≥24（k为分组变量数）时，可以采用Cochran’s Q检验。否则采用精确Cochran’s Q检验（计算Cochran’s Q 检验的样本量n时，需要减去三次测试结果都一致的样本数，如：111和000）

      4.对于假设条件的检验

      4.1 对于样本量的检验

      计算减去三次结果一样的样本量n

      转换-计算变量
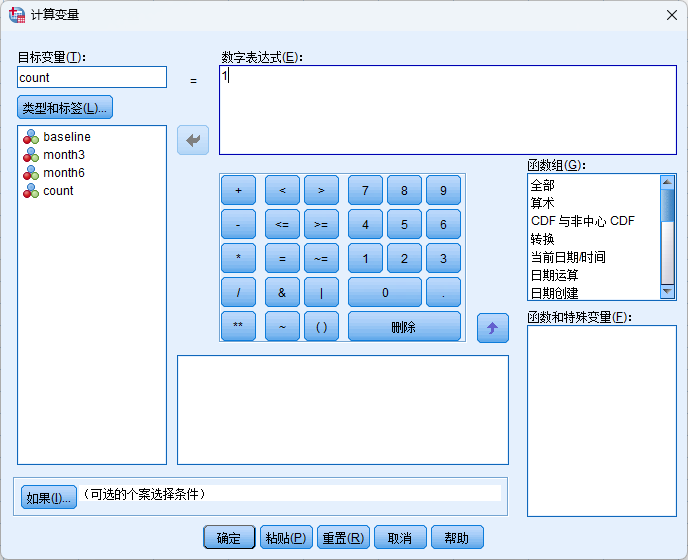
      image.png
      image.png
      image.png

  5. 先建立新字段count，并所有赋值为1；

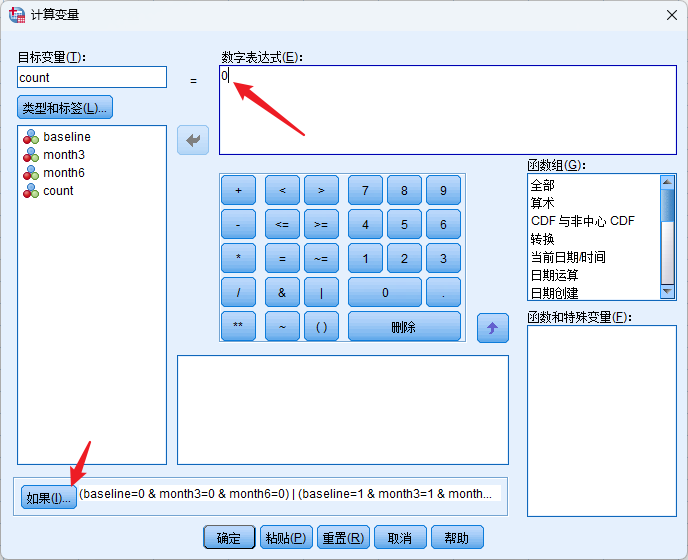
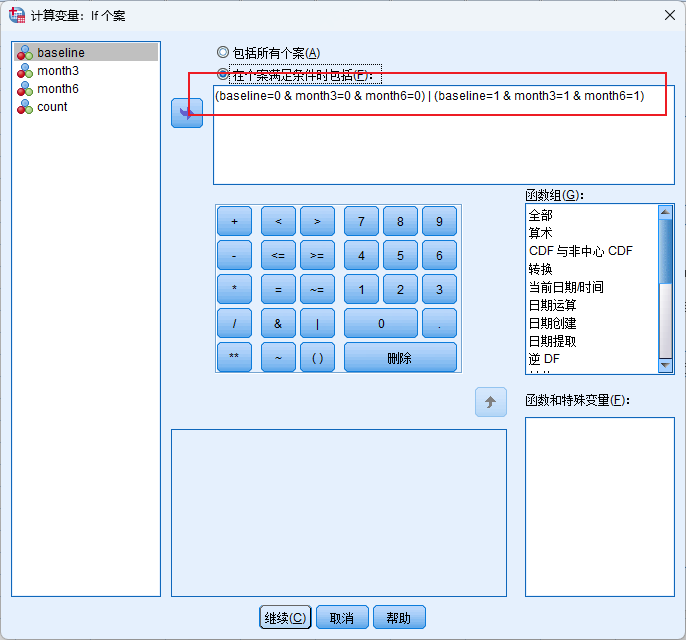
  6. 再将所有需要检测结果相同的个案（000，111）赋值为0，不进行计数；

对新变量进行统计
分析-表-定制表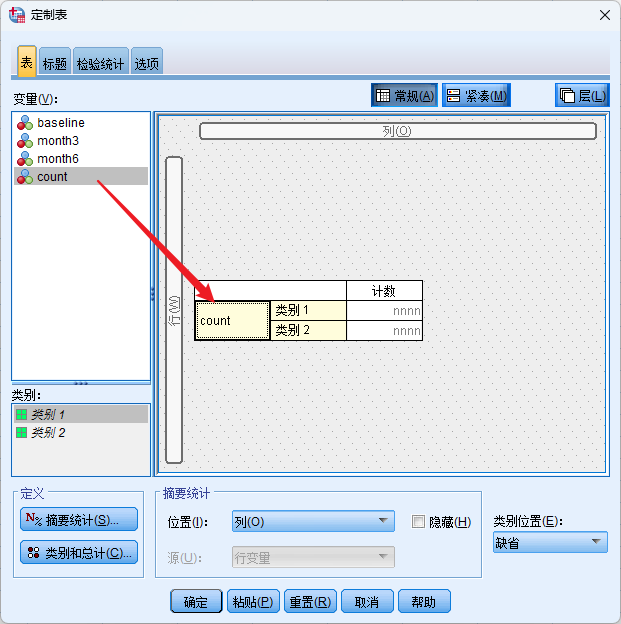
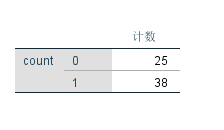
image.png
image.png

  1. 由统计结果可知，n=38≥4；

  2. 由于k=3，nk=114≥24，可以采用Cochran’s Q检验

    5.操作方式

    计算比例

    分析-描述统计-频率
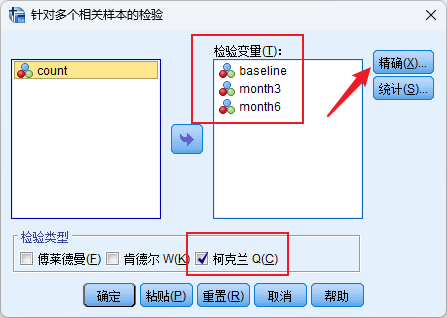
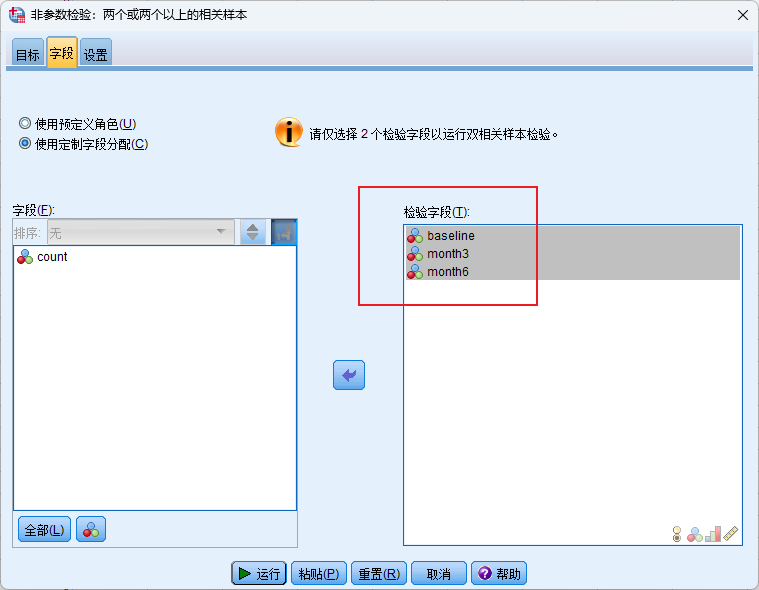
    image.png

    检验方法一：分析-非参数检验-相关样本

  3. 本方法比较适合能够通过假设4的数据检验

  4. 本方法有两两比较结果

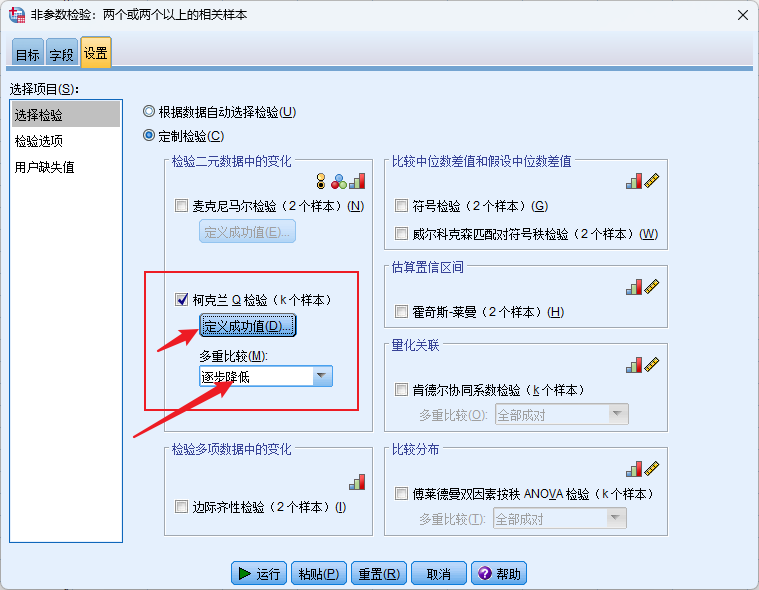
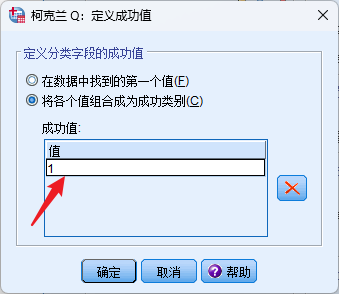
image.png
image.png
image.png

  1. 这里需要设置成功值，本案例中戒烟成功为成功。戒烟成功的代码为1； :::info

  2. 特别注意：多重比较时选择全部成对。因为全部成对后会有调整显著性数据 :::

    检验方法二：分析-非参数检验-旧对话框-k个相关样本

    Cochran’s Q检验

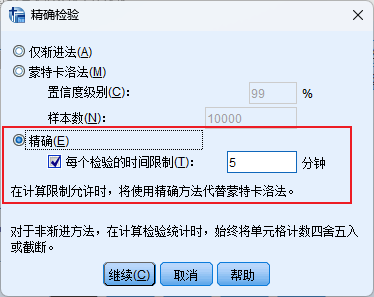
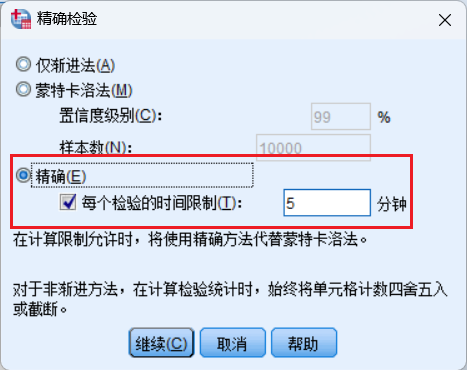
  3. 本方法无法进行两两比较，但可以进行精确Cochran’s Q检验

image.png
image.png

精确检验后的两两比较

对于不符合假设4时进行精确Cochran’s Q检验事后的两两比较，可采用经Bonferroni法校正的多重McNemar检验

分析-非参数检验-旧对话框-2个相关样本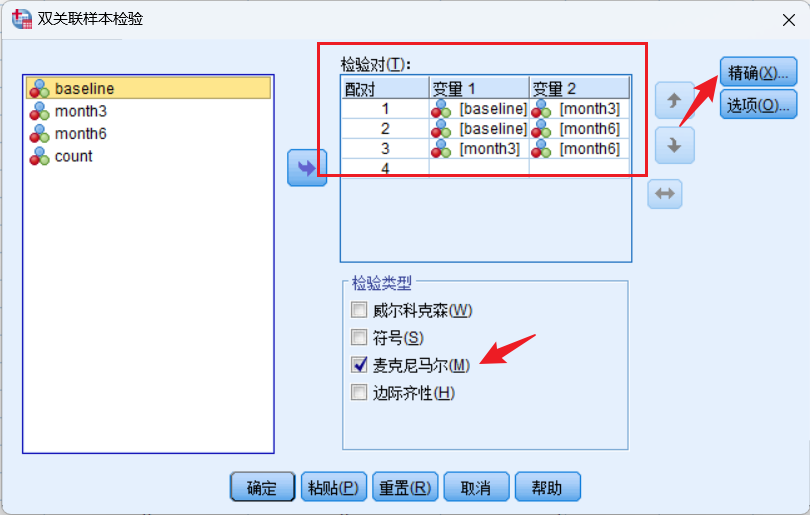
image.png
image.png

  1. 在旧对话框中可以实现各组之间的配对检验，但是前提需要自行配对；
  2. 在下方选择Bonferroni法校正的多重McNemar检验；

  3. 同时要选择精确选项。

    6.结果及解释

    6.1 结果的描述性统计

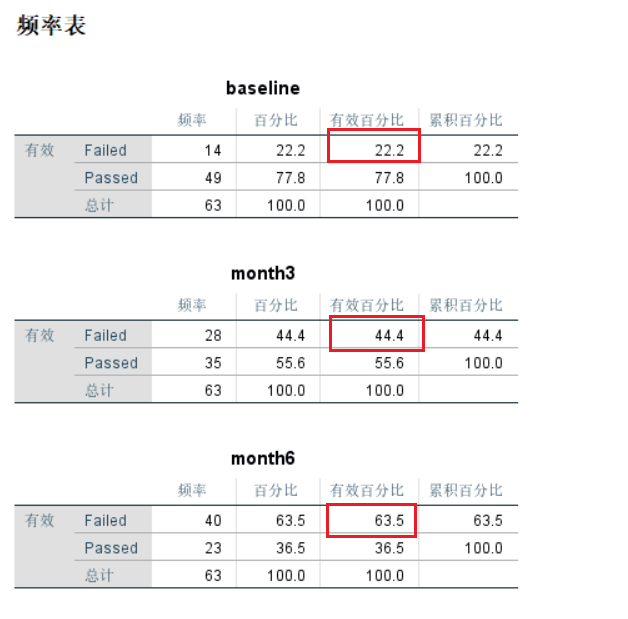
    image.png

  4. 基线、干预3个月和干预6个月时不吸烟的比例分别为22.2%、44.4% 和 63.5%。

    6.2 Cochran’s Q检验结果

    6.2.1 符合假设4的Cochran’s Q检验结果

    image.png :::info

  5. Cochran’s Q检验H0：三种处理的结果分布是相同的； :::

  6. 明显在检验结果中拒绝的原假设。认为三种处理结果（比例差异）不完全相同；

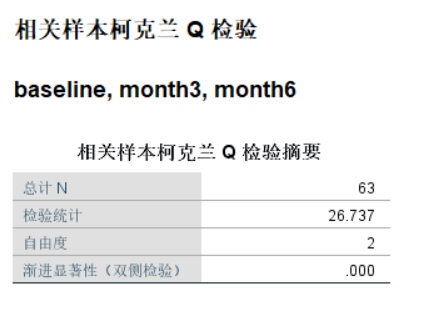
image.png

  1. Cochran’s Q检验统计量服从自由度为k-1的χ2分布。本研究的统计量为26.737，此时统计量可记为χ2 = 26.737，P<0.001。

    6.2.2 不符合假设4的精确Cochran’s Q检验结果

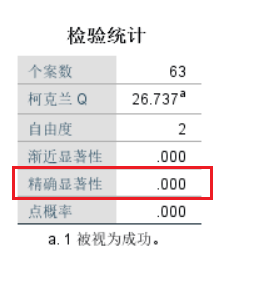
    image.png

  2. 统计量可记为Cochran’s Q=26.737，P<0.001，拒绝原假设，认为认为三种处理结果（比例差异）不完全相同。

    6.3 两两比较结果

    6.3.1 符合假设4的两两比较结果

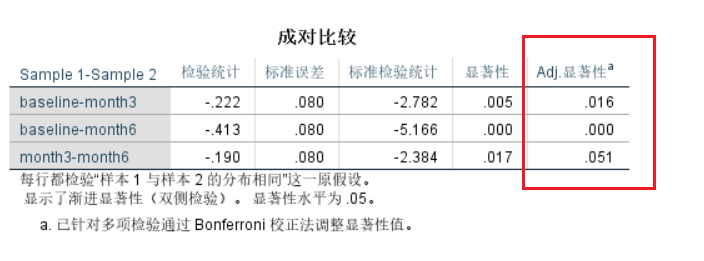
    image.png

  3. 由于为事后的两两比较，因此需要调整显著性水平（调整α水平），作为判断两两比较的显著性水平。依据Bonferroni法，调整α水平=原α水平÷比较次数。本研究共比较了3次，调整α水平=0.05÷3=0.0167。因此，最终得到的P值不能直接使用显著性列，而是使用Adj.显著性列，需要和0.0167比较，小于0.0167则认为差异有统计学意义

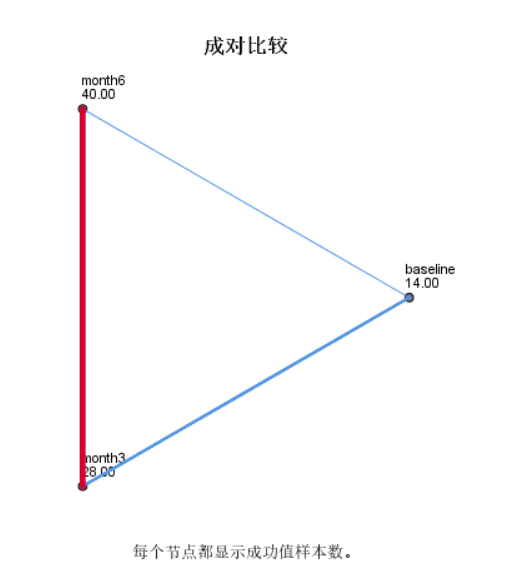
image.png

  1. 图中，连接线代表两两比较的结果，红色连接线代表两组间差异无统计学意义，蓝色连接线代表两组差异具有统计学意义。

    6.3.2 不符合假设4的两两比较结果

    不符合假设4时进行Bonferroni法校正的多重McNemar’s检验的结果
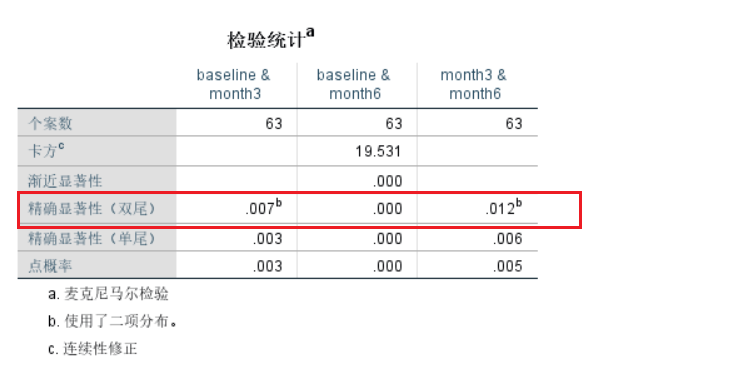
    image.png

  2. 由于是事后的两两比较，因此需要调整显著性水平（调整α水平），作为判断两两比较的显著性水平。依据Bonferroni法，调整α水平=原α水平÷比较次数。本研究共比较了3次，调整α水平=0.05÷3=0.0167。因此，最终得到的P值需要和0.0167比较，小于0.0167则认为差异有统计学意义。 :::warning

  3. 不符合假设4的两两比较结果为：基线和干预3个月时研究对象戒烟的比例差异有统计学意义（P=0.007），基线和干预6个月时研究对象戒烟的比例差异有统计学意义（P<0.001），干预3个月和干预6个月时研究对象戒烟的比例差异有统计学意义（P=0.012）（经Bonferroni法校正的α=0.0167）。 :::

    6.4 结果描述

  4. 基线和干预3个月时研究对象戒烟的比例差异有统计学意义（调整后P=0.016），基线和干预6个月时研究对象戒烟的比例差异有统计学意义（调整后P<0.001），而干预3个月和干预6个月时研究对象戒烟的比例差异无统计学意义。

    6.5 结论

    符合假设4时

  5. 基线、干预个月和干预6个月时，研究对象不吸烟的比例分别为22.2%、44.4% 和 63.5%。运用Cochran’s Q 检验对三个时间点吸烟状态进行调查，三个时间点戒烟比例的差异具有统计学意义，χ2=26.737，P<0.001；

  6. 采用Dunn’s检验（经Bonferroni法校正）进行事后的两两比较，基线和干预3个月时研究对象戒烟的比例差异有统计学意义（调整后P=0.016），基线和干预6个月时研究对象戒烟的比例差异有统计学意义（调整后P<0.001），而干预3个月和干预6个月时研究对象戒烟的比例差异无统计学意义（调整后P=0.051）。

    不符合假设4时

  7. 基线、干预个月和干预6个月时，研究对象不吸烟的比例分别为22.2%、44.4% 和 63.5%。运用Cochran’s Q 检验对三个时间点吸烟状态进行调查，三个时间点戒烟比例的差异具有统计学意义，Cochran’s Q= 26.737，P<0.001；

  8. 运用精确McNemar’s检验进行事后的两两比较（经Bonferroni法校正的α=0.0167）。基线和干预3个月时研究对象戒烟的比例差异有统计学意义（P=0.007），基线和干预6个月时研究对象戒烟的比例差异有统计学意义（P<0.001），干预3个月和干预6个月时研究对象戒烟的比例差异也有统计学意义（P=0.012）。