相关关系，不能证明因果关系。

1.研究目的

1. 研究两个连续性变量之间的相关性

   2.数据形式要求

   由于为有两个变量，故需要有两个字段
   

   3.需要满足的假设

2. 两个变量都是连续变量（观察）

3. 两个连续变量应当是配对的（即来源于同一个个体）（观察）
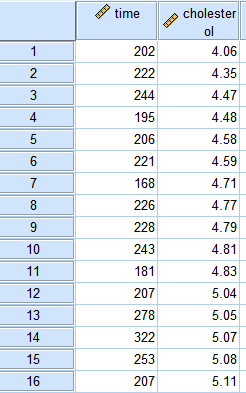
4. 两个连续变量之间存在线性关系，通常做散点图检验该假设（需要检验）
5. 两个变量均没有明显的异常值 （需要检验）

6. 两个变量符合双变量正态分布（需要检验）

   4.对假设的检验方式

   4.1 关于两个变量之间的线性关系

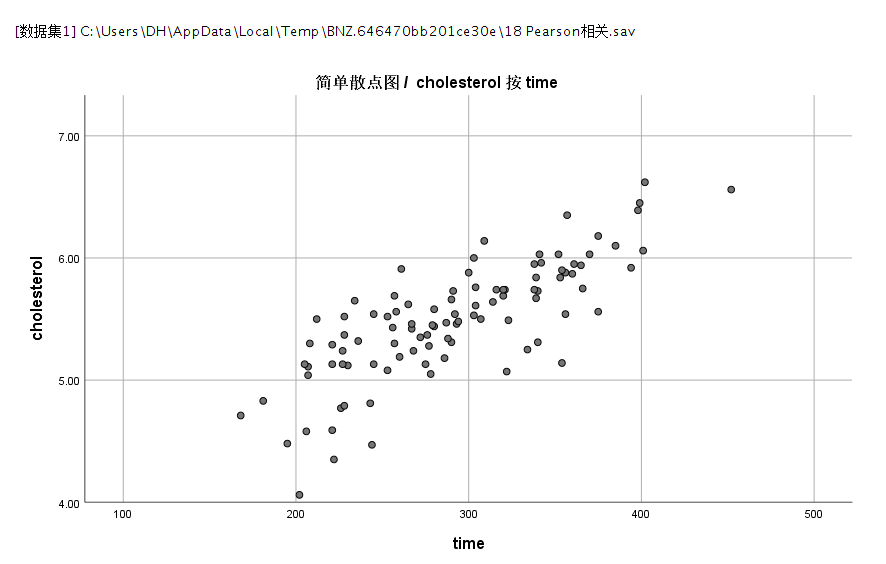
   关于两个变量之间的线性关系不需要进行检验，只需要作散点图观察有线性趋势即可

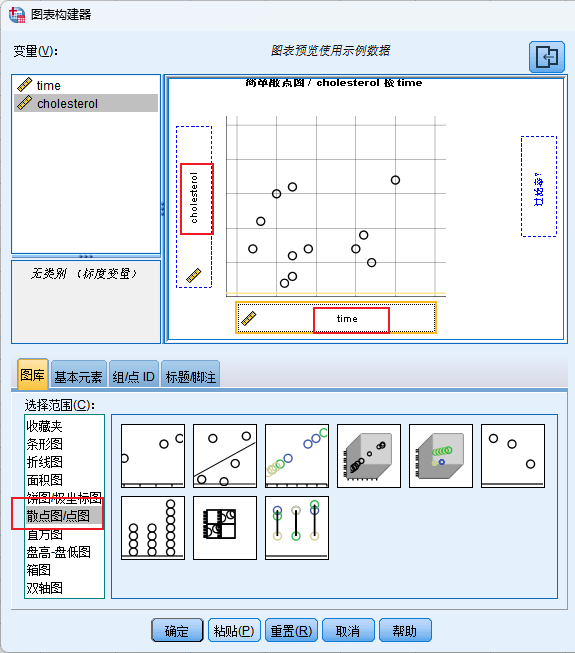
   图形-图表构建器

   

   散点图的阅读

   

7. 散点图中明显具备一定的线性趋势

   4.2 异常值的检验

   同T检验中的异常值检验

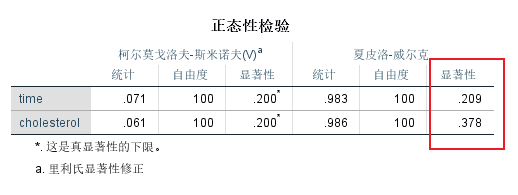
   4.3 双变量正态分布的检验

8. 检验Pearson相关系数的统计学意义时，要求双变量正态分布，但双变量正态分布难以评估；

9. 双变量正态分布的特性是：双变量正态分布存在则两个连续变量必然符合正态分布；但是两个连续变量符合正态分布未必代表双变量正态分布，但能够一定程度上保证双变量正态分布。因此，实际情况中，研究者可以分别检验两个连续变量的正态性，这样能够一定程度上保证双变量正态分布方法。

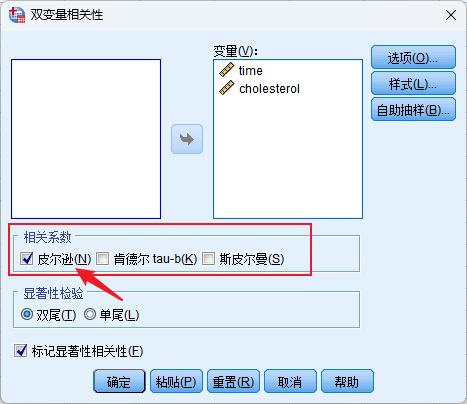
5.操作方法

分析-相关-双变量

6.结果及解释

6.1 相关系数的计算和检验

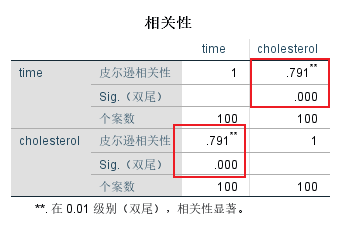
1. Pearson相关系数取值范围在[-1，+1]，负数代表负相关，正数代表正相关，0则代表不存在相关关系。两连续变量间相关的强弱没有规定数值，相关系数越接近0，相关关系越弱；越接近-1或+1，相关关系越强； :::info

2. Pearson相关系数假设检验H0：两个变量值之间的相关系数r有意义 :::

3. 本研究中，Pearson相关系数r=0.791，P<0.001，说明久坐时间（time）和胆固醇浓度（cholesterol）存在正相关关系，即久坐时间长与高胆固醇浓度有关

   6.2 结论

4. 本研究采用Pearson相关分析评价45-65岁男性中胆固醇浓度和每天久坐时间的关系。这两个变量间存在线性关系，根据Shapiro-Wilk检验符合正态分布（P>0.05），并且不存在异常值；

5. 每天久坐时间与胆固醇浓度间存在中度正相关关系，r=0.791，P<0.001