1.研究目的

两组配对(相关)样本所代表的总体间的均值是否有差异 :::tips 配对样本即为对一个个体进行处理后，得到的处理前数据和处理后数据 :::

2.数据形式要求

处理前后数据分别为两列。注意和独立样本T检验的数据形式不同。
image.png

3.需要满足的假设

  1. 观测变量为连续变量（观察）
  2. 分组变量包含两个分类、且相关（观察）
  3. 两个相关（配对）组别间观测变量的差值没有明显异常值（需要检验）

  4. 两个相关（配对）组别间观测变量的差值近似服从正态分布（需要检验）

    4.对假设的检验方式

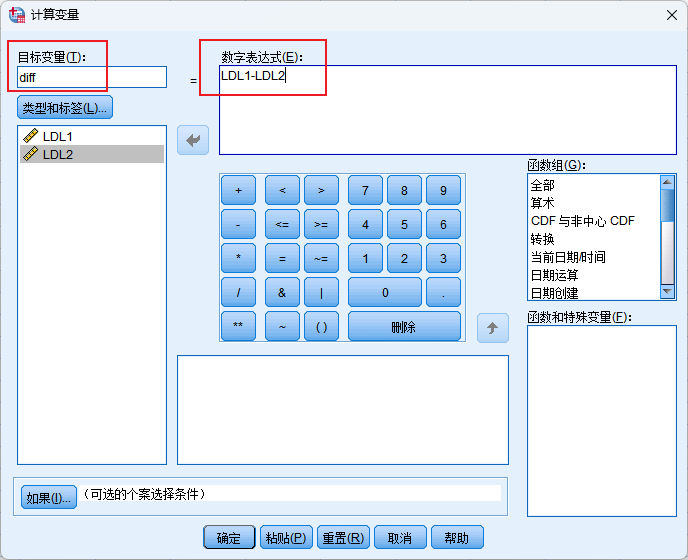
    做差值：转换-计算变量

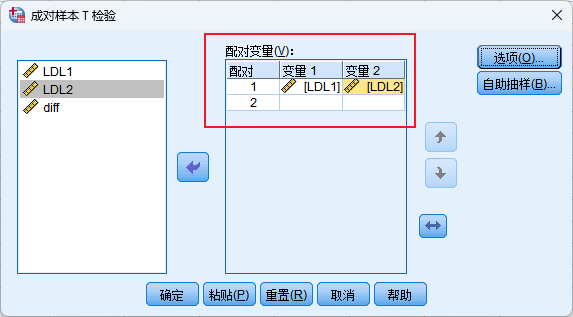
    image.png
    image.png

    对差值进行检验

    同独立样本T检验方法，不在赘述。

    5.操作方法

    分析-比较均值-配对样本T检验

    image.png

    6.结果及解释

    6.1 描述统计结果

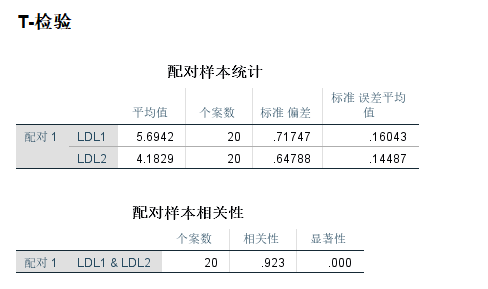
    image.png

  5. 研究对象基线LDL平均水平为5.69±0.72mmol/L，治疗后LDL平均水平为4.18±0.65 mmol/L

  6. 且治疗前后数据存在明显的相关关系，相关系数r=0.923

    6.2 假设检验结果

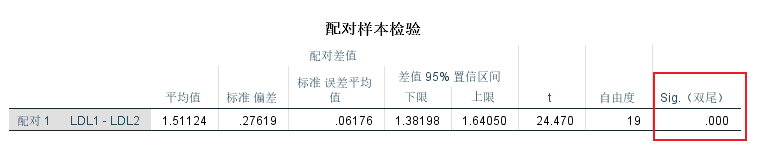
    image.png

  7. 药物治疗前后LDL的差值为1.51±0.28 mmol/L，差值的95%区间为：1.38-1.64 :::info

  8. 配对样本T检验H0：两个配对样本所代表的总体均数一致，没有差别（两个配对样本所代表的总体均数差值为0） :::

  9. 差值为正数表示治疗前LDL平均水平高于治疗后平均水平，差异有统计学意义（t=24.470，P<0.001）

    6.3 结论

  10. 利用配对样本t检验来判断研究对象经过某种药物治疗后，是否有助于降低LDL水平。数据以均数±标准差的形式表示。箱式图发现，无异常值。经Shapiro-Wilk检验，两组数据的差值服从正态分布（P=0.188）;

  11. 研究对象基线LDL平均水平为5.69±0.72mmol/L，治疗后LDL平均水平为4.18±0.65 mmol/L。药物治疗前后LDL的差值为1.51±0.28 mmol/L，差值的95% CI：1.38-1.64。治疗前LDL平均水平高于治疗后平均水平，差异有统计学意义（t=24.470，P<0.001）。