原题地址

方法一 双指针+贪心算法

这应该是解决本题最简单的做法，定义两个指针指向两个字符串，按照贪心算法思路，从前向后依次遍历，每次贪心地匹配靠前的字符，便是最优决策。

贪心算法可以取得全局最优解证明：假设当前要匹配字符 c ，而 c 在串 t 中出现的位置是 x1 , x2 并且 x1<x2 ，匹配 x1 是最优的，因为 x2 后面能取到的字符， x1 都能取到，并且 x1 还能取到 x1 , x2 之间的字符，有更大的匹配成功几率。所以匹配靠前的字符是最优的。

代码

class Solution:
    def isSubsequence(self, s: str, t: str) -> bool:
        i = j = 0  # 双指针
        m, n = len(s), len(t)
        while i < m and j < n:
            if s[i] == t[j]:
                i += 1
            j += 1
        return i == m

时空复杂度

最坏情况下完全遍历字符串 t 和子串 s ，所以时间复杂度为 O(m+n)
使用了常数个变量，所以空间复杂度为 O(1)

方法二 动态规划

方法一要想解决该题的 后续挑战 ，需要多次运行该函数，一个一个子串地来进行判断，时间复杂度就高了一个量级。

我们也发现了，方法一解决后续挑战，没有对字符串 t 的信息很好的利用，而动态规划算法可以收集字符串 t 的信息，这样无论多少个子串，都可以达到 一次收集，多次使用 的目的，需要判断的子串越多，动态规划就越比方法一好。

我们定义二维dp数组：
dp[i][j]表示从串 **t 的第 i 个位置开始往后，字符 j** 首次出现的位置
注意点：

1. 字符 j 表示的是字符在字母表中的序号，比如字符 a 应该为 0 ，所以 dp[i][0]=x 表示从第 i 个位置往后，字符 a 首次出现的位置是下标 x 处；
2. 从第 i 个位置开始，包括 i 处，所以如果 i 处字符为 j ，那么 dp[i][j] = i

有了以上条件，我们就可以得到dp的推导公式：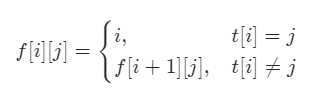

为了让边界上的 dp[tLen-1][j] 能正常处理，我们定义 dp[tLen][j] = tLen ， tLen 表示 t 的长度。这样如果 dp[i][j] == tLen ，则说明从 i 开始往后，没有字符 j 。

代码

class Solution:
    def isSubsequence(self, s: str, t: str) -> bool:
        sLen, tLen = len(s), len(t)
        dp = [[0] * 26 for i in range(tLen)]  # 定义二维dp数组
        dp.append([tLen] * 26)
        # 构造dp数组， ord()函数为获取字符的ascII码
        for i in range(tLen-1, -1, -1):
            for j in range(26):
                dp[i][j] = i if ord(t[i]) == j + ord('a') else dp[i+1][j]
        # 开始验证子串s是否在t中
        pos = 0
        for c in s:
            if dp[pos][ord(c) - ord('a')] == tLen:
                return False
            else:
                pos = dp[pos][ord(c) - ord('a')] + 1
        return True

时空复杂度

双重循环构造了dp数组，时间为 O(tLen * |∑|) , 其中|∑|为字母表长度26,而对子串进行验证只用了 O(sLen) ，所以时间复杂度为O(tLen * |∑|)

因为定义了二维数组dp，所以空间复杂度为O(tLen * |∑|)