原题地址

方法1-动态规划

思路

给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

看到这个题干，很容易想到 动态规划 。

既然要找具有最大和的连续子数组，那我们就把以第 i 个元素结尾的最大连续子数组都找出来，其中最大的那个就是全局的最大连续子数组。

定义 dp 数组，其中 dp[i] 表示以第 i 个元素结尾的最大和连续子数组。

递推公式为：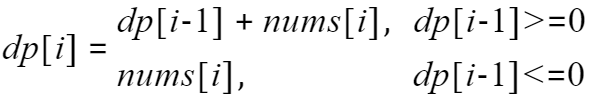
image.png
初试条件为 dp[0] = nums[0]

最后 dp 数组中最大的那个数就是最大和连续子数组的最大和。

代码1

  1. class Solution:
  2.     def maxSubArray(self, nums: List[int]) -> int:
  3.             n = len(nums)
  4.             if n == 0:  return 0
  5.             dp = [nums[0]]
  6.             for i in range(1, n):
  7.                 if dp[i-1] >= 0:
  8.                     dp.append(dp[i-1] + nums[i])
  9.                 else:
  10.                     dp.append(nums[i])
  11.             return max(dp)

代码2

其实我们可以发现，由于 dp[0]=nums[0] ，而 dp[i] 只与 dp[i-1] 和 nums[i] 有关，所以可以在原数组上修改，而不用定义 dp 数组，这样空间复杂度就为 O(1) 

  1. class Solution:
  2.     def maxSubArray(self, nums: List[int]) -> int:
  3.             if len(nums) == 0:  return 0
  4.             for i in range(1, len(nums)):
  5.                 if nums[i-1] >= 0:
  6.                     nums[i] += nums[i-1]
  7.             return max(nums)

时空复杂度

时间复杂度为 O(N) ，空间复杂度为 O(1)