原题地址

方法一 贪心算法

解决这道题，我们应该明白非常重要的一点。以[1,2,3] 为例，我们 在第一天买进，第三天卖出，等价于我们在第一天买进，第二天卖出，第二天再买进，第三天再卖出。

明白了这一点，我们就可以用 贪心算法 来做。我们只要发现第 i 天股票价格低于第 i+1 天的股票价格，就直接买进，第 i+1 天再卖出。

参考代码1 

  1. def maxProfit(self, prices: List[int]) -> int:
  2.     ans = 0
  3.     for i in range(1, len(prices)):
  4.         if prices[i] > prices[i-1]:
  5.             ans += (prices[i] - prices[i-1])
  6.     return ans


参考代码2**
其实也就是看相邻两天的差值(prices[i]-prices[i-1])，如果为正，就可以计入总利润。
所以也可以定义一个差值数组。

  1. class Solution: 
  2.     def maxProfit(self, prices: List[int]) -> int:
  3.         n = len(prices)
  4.         diff = []
  5.         for i in range(1, n):
  6.             diff.append(prices[i] - prices[i-1])
  7.         # 最后一天买入肯定要亏，所以把最后一天买入所获利润记为-1
  8.         diff.append(-1)
  9.         # diff[i]表示第i天买入第i+1天卖出所获利润
  10.         ans = sum([d if d > 0 else 0 for d in diff])
  11.         return ans

方法二 递归暴力求解（超时）

感觉这道题暴力比贪心还难想emmmm
虽然超时了，但是这道题还是值得用递归做一下的。
对于第 i 天，我们有三种选择：

  1. 什么也不做，即不买入，也不卖出；
  2. 当前不持有股票，并且买入；
  3. 当前持有股票，并且卖出；

这样我们就会得到一颗二叉树，对应这颗二叉树写代码就可以了。（图源自Liweiwei1419的题解）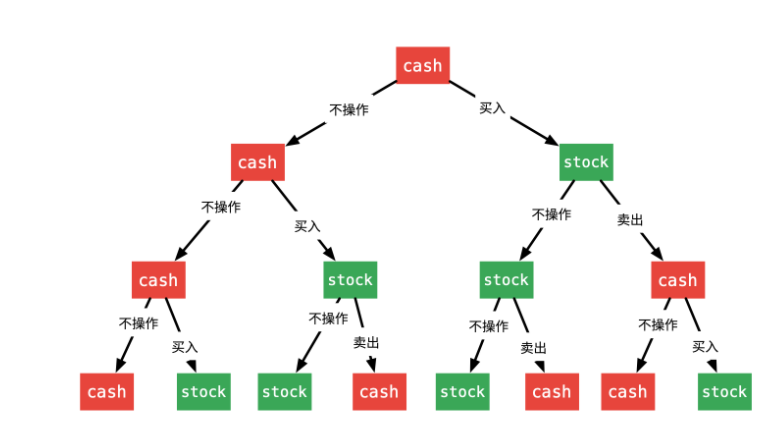
image.png
参考代码 

  1. class Solution: 
  2.     def maxProfit(self, prices: List[int]) -> int:
  3.         def dfs(i, status, profit, n):
  4.             if i == n:
  5.                 self.ans = max(self.ans, profit)
  6.                 return None
  7.             #  1.当前什么也不做
  8.             dfs(i+1, status, profit, n)
  9.             # 2.当前买入
  10.             if status == 0:
  11.                 dfs(i+1, 1, profit-prices[i], n)
  12.             # 3.当前持有股票，卖出
  13.             else:
  14.                 dfs(i+1, 0, profit+prices[i], n)
  16.         n = len(prices)
  17.         if n < 2:
  18.             return 0
  19.         self.ans = 0
  20.         '''
  21.         prices
  22.         i :当前是第几天
  23.         status: 当前状态 为0表示不持有股票，为1表示持有股票
  24.         profit: 当前利润
  25.         n: 数组长度
  26.         '''
  27.         dfs(0, 0, 0, n)
  28.         return self.ans