原题地址（困难）

此题虽是困难，但是做法超级多啊，而且也有很容易想到的做法。

方法1—顺序合并

思路

这是我最想想到的做法，很简单。
两个链表合并我们都会，多个链表呢？用个循环呗。就这么简单。

代码

class Solution {
public:
    ListNode* mergeKLists(vector<ListNode*>& lists) {
        if(lists.size() == 0)   return {};
        ListNode* dummy = new ListNode(0);  //虚头结点
        ListNode* p, *q, *pre, *tmp;
        dummy->next = lists[0];
        for(int i=1; i<lists.size(); i++) {
            // 把第i个链表和ret合并在一起
            pre = dummy;
            p = dummy->next;
            q = lists[i];
            while(q && p) {
                if(q->val <= p->val) {
                    tmp = q;
                    q = q->next;
                    pre->next = tmp;
                    tmp->next = p;
                }
                else{
                    p = p->next;
                }
                pre = pre->next;
            }
            if(!p && q) {
                pre->next = q;
            }
        }
        return dummy->next;
    }
};

时空复杂度

时间复杂度

假设链表最长长度为，共有个链表，那么时间复杂度为
因为有个链表，第一次合并，是合并第一、第二个链表；第二次合并，实质是第一、二个链表合并后的链表，再和第三个链表合并，因此所耗费时间为，所以时间复杂度为

空间复杂度

因为是原地修改，所以空间复杂度为，如果不是原地修改的话，空间复杂度就为

方法2—分治合并

思路

可以用分治的思路对方法一进行优化，从而使时间复杂度降低。
盗用官方图：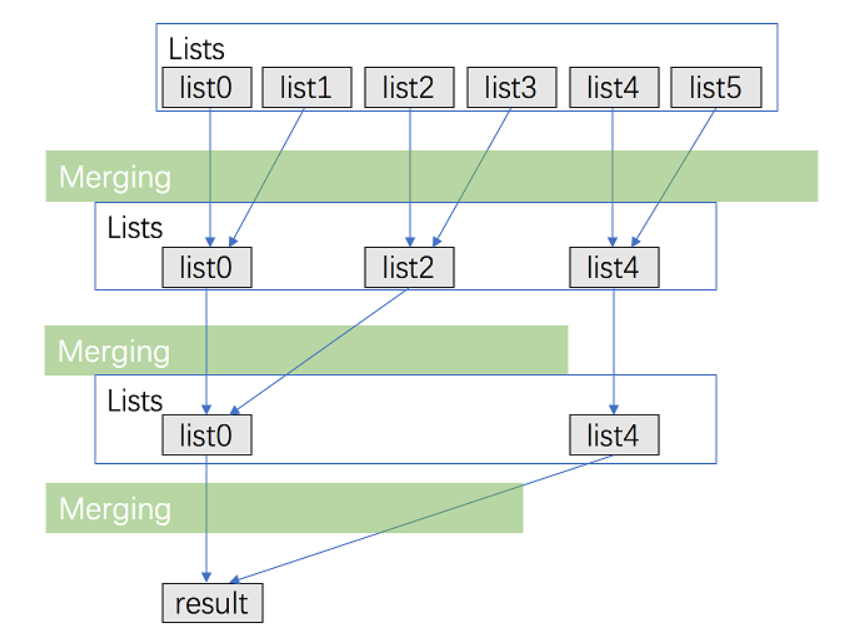

代码

class Solution {
public:
    ListNode* mergeTwoLists(ListNode* a, ListNode* b) {
        if(!a || !b)    return a ? a : b;
        ListNode *dummy = new ListNode(0);
        ListNode *p = a, *q = b, *tail = dummy;
        // 尾插法
        while(p && q) {
            if(p->val <= q->val) {
                tail->next = p;
                p = p->next;
            }
            else{
                tail->next = q;
                q = q->next;
            }
            tail = tail->next;
        }
        tail->next = p ? p : q;
        return dummy->next;
    }
    ListNode* merge(vector<ListNode*> lists, int l, int r){
        if(l == r)  return lists[l];
        if(l > r)   return nullptr;
        int mid = (l + r) / 2;
        ListNode* a = merge(lists, l, mid);
        ListNode* b = merge(lists, mid+1, r);
        return mergeTwoLists(a, b);
    }
    ListNode* mergeKLists(vector<ListNode*>& lists) {
        int n = lists.size();
        if(n == 0)   return nullptr;
        return merge(lists, 0, n - 1);
    }
};

时空复杂度

时间复杂度

还是假设链表最长长度为，共有个链表。
第一次合并，共合并次，每次耗费时间2n；
第二次合并，共合并次，每次耗费时间4n;
第i次合并，共合并 次，每次耗费时间;
所以总耗费时间为，所以时间复杂度为

空间复杂度

递归使用

方法3—优先队列

思路

这可能是这道题的最优方法，也是出题人所希望看到的方法。
那就是维护一个优先队列，每次弹出所有链表中最小值的那个节点，再用这个链表的下一个节点补上，直至所有链表都被弹完。

代码

class Solution {
public:
    struct Status{
        int val;
        ListNode* node;
        bool operator < (const Status& s) const {
            return val > s.val;
        }
    };
    ListNode* mergeKLists(vector<ListNode*>& lists) {
        priority_queue<Status> q;
        for(auto list : lists) {
            if(list)    q.push({list->val, list});
        }
        ListNode head, *tail = &head;
        while(!q.empty()) {
            auto tmp = q.top();
            q.pop();
            tail->next = tmp.node;
            tail = tail->next;
            if(tmp.node->next)  q.push({tmp.node->next->val, tmp.node->next});
        }
        return head.next;
    }
};

时空复杂度

时间复杂度

长度为k的优先队列插入删除元素耗费时间都是，k个链表元素总数量不超过，所以时间复杂度为

空间复杂度