原题地址（困难）

方法1—递归

思路

开始我想到的是递归，改了多次以后，还是超时。。。。
不过写的也挺不容易的，还是把这个方法贴出来吧。

思路流程如下：

代码

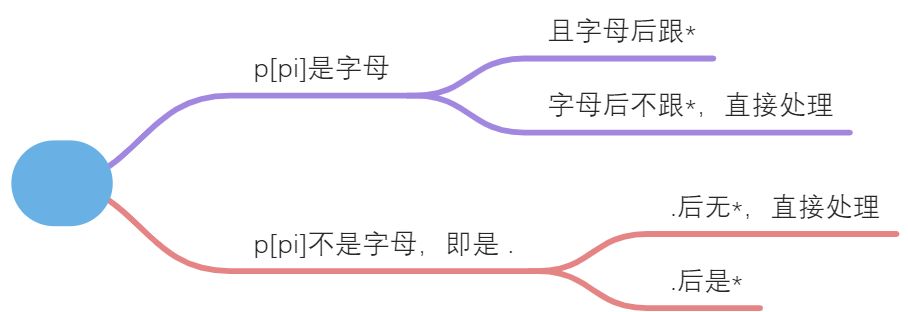
class Solution {
public:
    bool isMatch(string s, string p) {
        int si = 0, pi = 0, n = s.size(), m = p.size();
        return dfs(s, p, si, pi, n, m);
    }
    bool dfs(string s, string p, int si, int pi, int n, int m ) {
        // 边界条件
        if(si < n && pi >= m)   return false;
        else if(si >= n){
            while(pi + 1 < m && p[pi+1] == '*')
                pi += 2;
            if(pi < m)  return false;
            else    return true;
        }
        // 递归
        if(p[pi] != '*' && p[pi] != '.'){  // p[pi]是字母
            if(pi+1 >= m || (pi+1 < m && p[pi+1] != '*')) {
                if(p[pi] != s[si])  return false;
                else    return dfs(s, p, si+1, pi+1, n, m);
            }
            else {   // 字母后跟*      c* 可能匹配：{null, c, cc, ccc, ...}
                bool res = dfs(s, p, si, pi+2, n, m);  // 把null单拿出来
                // 再匹配其他的情况
                char tmp = p[pi];
                while(si < n && s[si] == tmp){
                    res |= dfs(s, p, si+1, pi+2, n, m);
                    si++;
                }
                return res;
            }
        }
        else if(p[pi] == '.') { // p[pi]是.
            if(pi+1 >= m || (pi+1 < m && p[pi+1] != '*'))  // 单点匹配，后无*
                return dfs(s, p, si+1, pi+1, n, m);
            else {  // .*可匹配任意
                bool res = dfs(s, p, si, pi+2, n, m);
                while(si < n) {
                    res |= dfs(s, p, si+1, pi+2, n, m);
                    si++;
                }
                return res;
            }
        }
        return false;
    }
};

方法2—动态规划

思路

动态规划才是正解。。。。
不过大体思路和递归一样，也是分情况讨论。
dp[i][j] 表示s的前i个字符和p的前j个字符是否匹配
**
直接看的官方题解

代码

class Solution {
public:
    bool isMatch(string s, string p) {
        int m = s.size();
        int n = p.size();
        auto matches = [&](int i, int j) {
            if (i == 0) {
                return false;
            }
            if (p[j - 1] == '.') {
                return true;
            }
            return s[i - 1] == p[j - 1];
        };
        vector<vector<int>> f(m + 1, vector<int>(n + 1));
        f[0][0] = true;
        for (int i = 0; i <= m; ++i) {
            for (int j = 1; j <= n; ++j) {
                if (p[j - 1] == '*') {
                    f[i][j] |= f[i][j - 2];
                    if (matches(i, j - 1)) {
                        f[i][j] |= f[i - 1][j];
                    }
                }
                else {
                    if (matches(i, j)) {
                        f[i][j] |= f[i - 1][j - 1];
                    }
                }
            }
        }
        return f[m][n];
    }
};

时空复杂度

空间复杂度O(NM)
时间复杂度O(NM)