原题地址（中等）

方法1—递归

思路

这题是当时考研初试时做过的非常经典的题目。

中序遍历为“左根右”，后序遍历为“左右根”。
所以给定中序和后序、中序和前序，都可以还原出树，但是给定前序和后序，不可以还原。

那么本题的思路是什么呢？

就是从后序中找出根，根据这个根的值（因为此树中无重复元素）可以把中序序列一分为二，左边为左子树，右边为右子树。再根据左右子树的元素个数，把后序序列也一分为二。最后分别对该根的左右子树进行递归处理，重复上述过程。
**
看不明白没关系，直接看例子，看完肯定会懂。

设 inorder = [9, 3, 15, 20] ， postorder = [9, 20 ,15 3]

  1. 从当前后序中找出根，为3，再用3把中序序列一分为二，分别为 [9], [15, 20] ，根据左右子树中元素的个数，同样也可以把后序序列一分为二。（因为后序序列中最后一个元素一定是当前的根，去掉这个根，剩下的元素中，前1个就是左子树的元素，后2个就是右子树的元素）。此时我们已经得到了这样的结构：

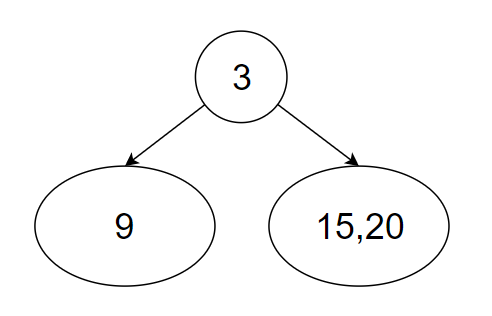
image.png
左子树有元素9， 右子树有元素15,20。但是至于左右子树的具体结构，还未知。

  1. 递归处理左右子树。
    • 对于左子树，当前的后序序列为 9 ，从该序列中找出根（也就是最后一个元素），重复步骤1
    • 队友右子树，当前的后序序列为 20, 15 ，从该序列中找出根（也就是最后一个元素），重复步骤1

代码

  1. class Solution {
  2. public:
  3.     vector<int> inorder, postorder;
  4.     map<int, int> m;
  5.     TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
  6.         this->inorder = inorder;
  7.         this->postorder = postorder;
  8.         for(int i=0; i<inorder.size(); i++) m[inorder[i]] = i;
  9.         return dfs(0, inorder.size()-1, 0, postorder.size()-1);
  10.     }
  12.     TreeNode* dfs(int inLeft, int inRight, int postLeft, int postRight) {
  13.         if(inLeft > inRight)    return nullptr;  // 递归终止条件
  14.         //创建当前根
  15.         int rootVal = postorder[postRight];
  16.         TreeNode* root = new TreeNode(rootVal);
  17.          //找到当前根节点在中序数组中的下标，用来把中序序列一分为二
  18.         int i = m[rootVal]; 
  19.         //递归处理左右子树
  20.         //  i-inLeft是左子树的元素个数
  21.         root->left = dfs(inLeft, i-1, postLeft, postLeft+i-inLeft-1);
  22.         root->right = dfs(i+1, inRight, postLeft+i-inLeft, postRight-1);
  23.         return root;
  24.     }
  25. };

时间复杂度

把中序序列中的所有结点都遍历且仅遍历了一次，所以为 O(N)

空间复杂度

最坏情况下栈的深度是 N ，哈希表使用的空间是 N ，所以为O(N)