原题地址(简单)
方法1-二分查找
思路
这道题我拿到手先用 sqrt 函数试了一下,可以过,hhhhh
然后不用自带函数的话,肯定就是二分查找了。
最简单的二分查找思路就是设区间为 [0, x] 找出满足value**2<=x 的最大的那个 value 。
代码
注意细节(返回值为 high ),分析循环中的语意可知:
- 如果有
mid**2 == x,就直接返回了; - 如果不是,就得寻找满足
mid**2 < x中最大的那个mid;
接下来分析如何找满足条件下最大的那个mid。(以下不包括class Solution:def mySqrt(self, x: int) -> int:low, high = 0, x # 左右区间while low <= high:mid = (low + high) // 2if mid**2 == x:return midelif mid**2 > x:high = mid - 1else:low = mid + 1return high
mid**2 == x,因为它直接在循环中返回了)
要注意,循环终止条件就是 high<low
- 开始
mid**2 > x的情况:- 会一直执行
high = mid - 1,high不断减小,直到mid**2 < x,此时low又会不断增加,直到low==high,此时两者所指就是我们要找的数,但是循环不会就此停止,low继续增加,循环条件破坏,循环终止,而此时high还是指向我们要找的数,返回high。
- 会一直执行
- 开始
mid**2 < x的情况:- 也就是情况1的后半部分。
low会不断增加,直到low==high,此时两者所指就是我们要找的数,但是循环不会就此停止,low继续增加,循环条件破坏,循环终止,而此时high还是指向我们要找的数,返回high。
- 也就是情况1的后半部分。
如果还是不明白上述的论证,大可以举几个例子看一看,你会发现最后结束时我们要找的数都是 high 。
二分查找思路很简单,但是像“返回值应该是谁”、“循环终止条件”、“判断是有没有等号”、“ high=mid+1 还是 high=mid ”这种细节非常多,这也是二分查找的难点所在。
关于二分查找,可以看一下liweiwei大佬的文章
weiwei大佬博客 weiwei大佬力扣题解
时空复杂度
众所周知,二分查找时间复杂度为 O(logN) ,这题也不例外;
空间复杂度为 O(1)
方法2—牛顿迭代法
如果学过数值分析或者机器学习的同学,应该都熟悉牛顿迭代法(牛顿法)。它是一种求解方程近似值的方法。
牛顿法产生背景
多数方程不存在求根公式,因此求精确根非常困难,甚至不可解,从而寻找方程的近似根就显得特别重要。方法使用函数的泰勒级数的前面几项来寻找方程的根。牛顿迭代法是求方程根的重要方法之一,其最大优点是在方程的单根附近具有平方收敛,而且该法还可以用来求方程的重根、复根,此时线性收敛,但是可通过一些方法变成超线性收敛。另外该方法广泛用于计算机编程中。 ——摘自《百度百科》
牛顿法迭代公式
牛顿法的核心是以直代曲,一般我们都用一次泰勒级数,也就是线性方程来作为切线。
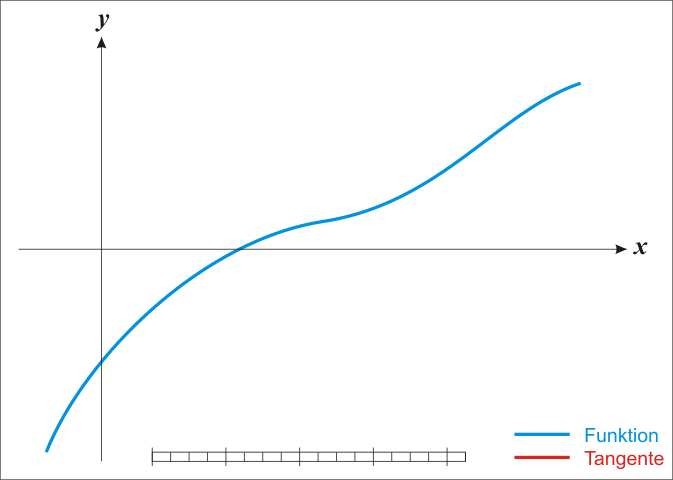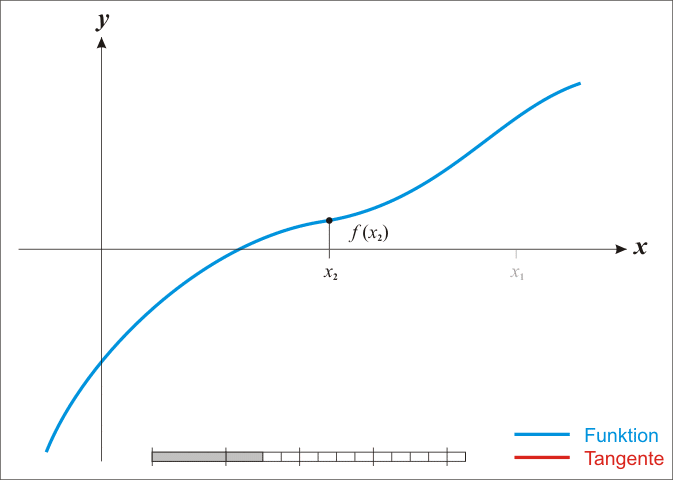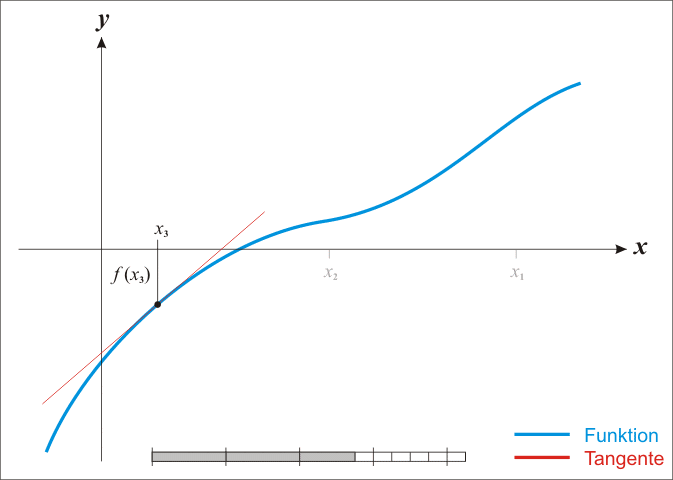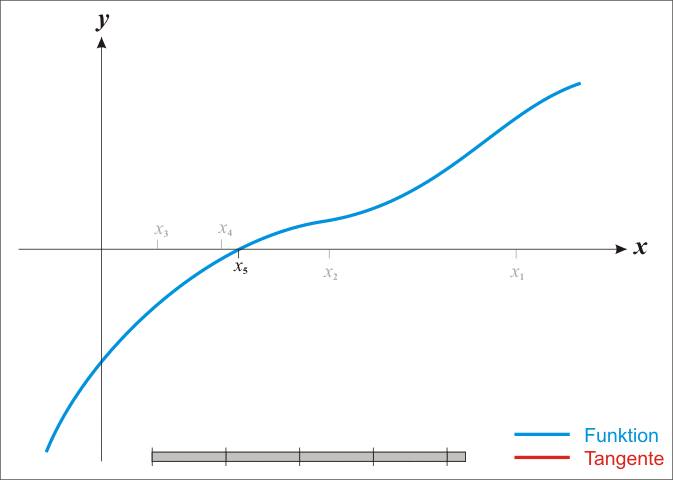
迭代过程如下:在 x0 点做一条切线,找到这条切线和x轴的交点 x1 ,再以 x1 所对应的曲线方程做一条切线,再找到这条切线和x轴的交点 x2 ,以此类推,直至收敛。
公式推导**:在此题中,我们可以设曲线方程为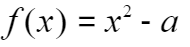 ,我们的目的就是求解出
,我们的目的就是求解出 x 使得 f(x)=0 。
设已知点 x0 ,则此点处的斜率为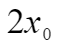 ,对应切线方程为
,对应切线方程为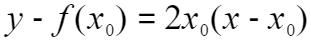 ,令
,令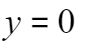 ,求出
,求出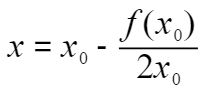 ,又因为
,又因为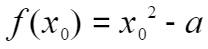 ,代入得
,代入得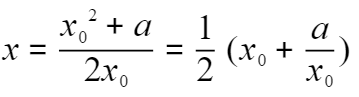
所以最后的递推公式为: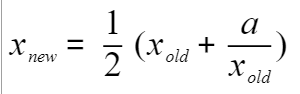
图解如下:
代码
注:牛顿法得到的可能是浮点数,最后我们要把结果转化为 int 型整数(也就是去掉小数部分)
class Solution:def mySqrt(self, x: int) -> int:# 这里的x就是公式中的aif x == 0: return 0new = 1while True:old = newnew = (old + x / old) / 2 # 递推公式if abs(new - old) < 1e-5: # 两者误差极其小,我们就视为相等,迭代结束breakreturn int(new)
时空复杂度
此方法二次收敛,时间复杂度为 O(logN)
空间复杂度 O(1)

