153. 寻找旋转排序数组中的最小值

原题地址（中等）

方法1—暴力

对，你没看错，就是遍历一遍，找出最小值。

本来我以为肯定会超时，结果没有，emmm。

但遍历找最小值绝不是出这道题的目的。

方法2—二分

思路

这道题的正确解法应该是二分查找。

但我们又发现，普通的二分查找不能够解决问题，那怎么办呢？

先分析一下这道题。按照题意，这道题的数组差不多是这个样子：

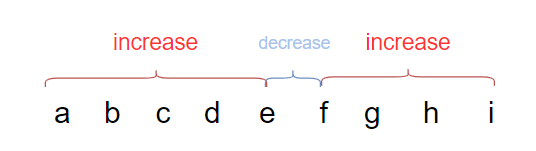
先是一个局部递增，然后是两个数的递减（数组中最大的数和最小的数），再然后是一个局部递增。
**
注意：整个数组只有两个相邻元素间有递减关系，其余都是局部递增关系。

**
那么我们来分析一下在二分查找中， low , mid , high 所在位置的三个数的关系：
左代表nums[low]，中代表nums[mid]，右代表nums[high]

• 左<中<右：没有进行旋转，去左侧区间进行查找；
• 中<左<右：中<左说明进行了旋转，并且进行了较大幅度的旋转（前面超过一半的元素都旋转到了后面），例如 nums=[5,6,1,2,3,4] 时， nums[mid]=1 ，这时候不可能有左<右。事实上，中<左，中<右说明两侧区间都不是递增的，由注意点可知，这是不存在的情况。
• 左<右<中：右<中说明进行了旋转，而且是较小幅度的旋转，例如nums=[3,4,5,6,1,2] 时，这时候不可能有左<右。事实上，只要进行了旋转，就不可能有左<右。
• 右<左<中：右<左说明进行了旋转，左<中说明左侧区间是递增的，最小值一定在右侧，例如nums=[3,4,5,6,1,2] ，所以去右侧区间查找；
• 中<右<左：右<左说明进行了旋转，中<左说明左侧区间非递增，由注意点可知，右侧区间一定是递增的，所以去左侧区间查找；
• 右<中<左：右<中说明右侧区间非递增，中<左说明左侧区间非递增，由注意点可知，不存在这种情况。

综上，共有三种可能出现：

1. 左<中<右：去左侧区间
2. 右<左<中：去右侧区间
3. 中<右<左：去左侧区间

到这里为止，二分查找的判断条件就呼之欲出了，总结上面三种情况，得出：
如果中<右，去左侧区间；否则，去右侧区间

代码

class Solution:
    def findMin(self, nums: List[int]) -> int:
        n = len(nums)
        low, high = 0, n - 1
        while low < high:
            mid = low + (high - low) // 2
            if nums[mid] < nums[high]:
                high = mid
            else:
                low = mid + 1
        return nums[low]

时空复杂度

时间复杂度 O(logN) ，空间复杂度 O(1)