Floyd龟兔赛跑算法

一个跑得快的人和一个跑得慢的人在一个圆形的赛道上赛跑，会发生什么？
在某一个时刻，跑得快的人一定会从后面赶上跑得慢的人。 Floyd算法就是用来判断两人是否相遇以及算出在哪里相遇的算法。

算法

Floyd 的算法被划分成两个不同的 阶段 。

第一阶段

• 找出列表中是否有环，如果没有环，可以直接返回 null 并退出。否则，用相遇节点来找到环的入口。
• 方法：初始化两个指针—快慢指针。每次快指针移动两步，慢指针移动一步。直到两指针相遇或者快指针为空，分别说明出现了环或者无环。

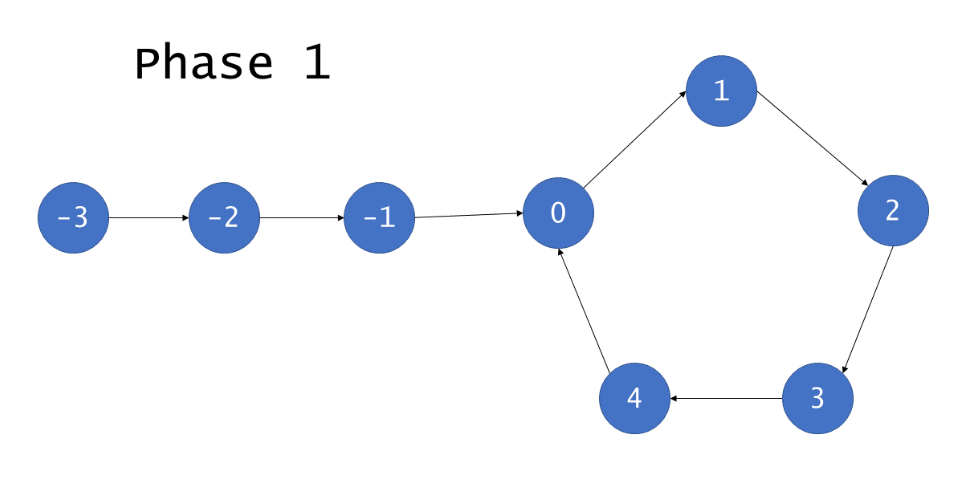
环中的节点从 0 到 C−1 编号，其中 C 是环的长度。非环节点从 −F 到 −1 编号，其中 F 是环以外节点的数目。
F次迭代以后，慢指针指向了 0 且快指针指向某个节点 h，其中 h ≡ F(modC) 。这是因为快指针在 F 次迭代中遍历了 2F个节点，且恰好有 F 个在环中。继续迭代C−h 次，慢指针显然指向第C−h 号节点，而快指针也会指向相同的节点。原因在于，快指针从 h 号节点出发遍历了 2(C−h) 个节点。h+2(C−h) = 2C−h ≡ C−h(modC)*

第二阶段

• 找出环的入口。
• 方法：初始化两个指针，一个指向链表的头，一个指向相遇点，每次将它们向前移动一步，直到它们相遇，相遇点便是环的入口。

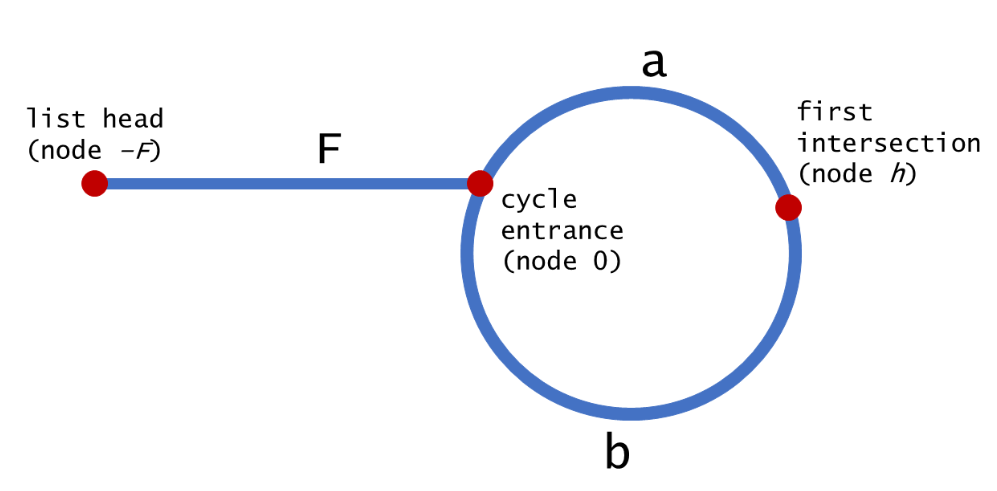
经过第一阶段后，两指针在C-h点相遇，把该点重新记为h（只是一个符号而已，与第一阶段的h不是一个含义，换成其他符号也无所谓），下面证明第二阶段的两个指针能在入口处相遇。
tortoise**表示慢指针，hare表示快指针，由第一阶段知**
2 * distance(tortoise) = distance(hare)** 即 2 * (F + a) = F + a + n(b + a) 得出 **F = (n-1)(a+b) + b
所以从头结点和从h结点同时出发，将会在入口相遇。