原题地址（困难）

方法1—回溯

思路

赫赫有名的八皇后问题的变种。
其实这题不是很难，就是最基础的回溯解法。但是要剪枝，也就是每次都要判断第i行第j列是否可以放置皇后，即判断(i, j)位置是否满足行不重复、列不重复、主对角线方向不重复、副对角线方向不重复。

行和列我们肯定非常容易判断，我们按行遍历回溯，行就不需要判断了，列的话用一个一维vector来存储就好了，被占用了第k列，就记 column[k] = 1 。
至于主对角线方向不重复、副对角线方向，其实和列一样，各用一个一维vector来判断就可以，只不过需要你找出一些规则。

盗用一些官方的图
首先明确，无论主对角线还是副对角线方向，数组大小都是2*n+1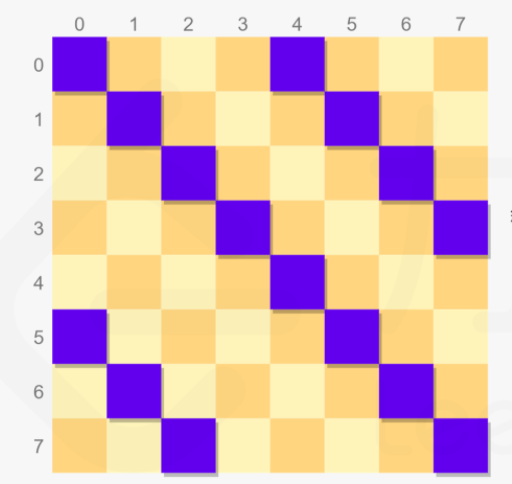

我们定义主对角线方向的数组为 a ，从右上角到左下角，下标依次为 0, 1, ..., 2n-1
a[0] 对应图中的一个位置，就是(0, 7)
a[1] 对应两个位置，就是(0, 6) , (1, 7)
…..
a[2n-1] 对应一个位置，就是(7, 0)
我们可以发现，同一列中，行值越大，在a中越靠后；同一行中，列值越大，在a中越靠前。所以对应公式中一定有 i-j
通过尝试，发现最终公式为： i+(n-1)-j ，即 (i, j) 对应 a[i+n-1-j]
**

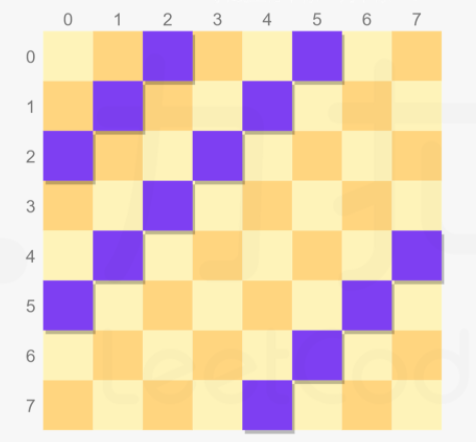
同理得到副对角线方向的对应公式： i+j

代码

class Solution {
public:
    vector<int> a, b, column;
    vector<string> v;
    vector<vector<string>> ans;
    vector<vector<string>> solveNQueens(int n) {
        // 主对角线方向，副对角线方向，列方向
        a.resize(2*n+1, 0);
        b.resize(2*n+1, 0);
        column.resize(n, 0);
        dfs(0, n);
        return ans;
    }
    void dfs(int row, int n) {
        if(row == n){
            ans.push_back(v);
            return;
        }
        // 对第row行的每一列
        for(int j=0; j<n; j++){
            //如果(row, j)这个位置满足行列左斜右斜都没有重复皇后
            if(!a[row+n-1-j] && !b[row+j] && !column[j]){
                a[row+n-1-j] = b[row+j] = column[j] = 1;
                string s(n, '.');
                s[j] = 'Q';
                v.push_back(s);
                dfs(row+1, n);
                v.pop_back();
                a[row+n-1-j] = b[row+j] = column[j] = 0;
            }
        }
        return;
    }
};

时空复杂度

时间复杂度 O(N!)
空间复杂度 O(2N+1)

方法2—

思路

代码

时空复杂度