本文介绍了堆排序的原理，并在最后给出了代码实现。

堆排序是一种树形选择排序，由弗洛伊德提出，它的特点是：在排序过程中，将L[1...n]看成一棵完全二叉树的顺序存储结构，利用完全二叉树中双亲结点和孩子结点之间的内在关系，在当前无序区选择关键字最大（或最小）的元素。

1. 堆的定义

n个关键字序列L[1...n]称为堆，当且仅当该序列满足：

L(i)<=L(2i) && L(i)<=L(2i+1)
L(i)>=L(2i) && L(i)>=L(2i+1)

满足第一种情况的叫做小顶堆（小根堆），满足第二种情况的叫做大顶堆（大根堆）

显然，大根堆中根元素为最大的元素，且每个子树的根元素都是该子树的最大元素。小根堆则反之。

如图为大根堆。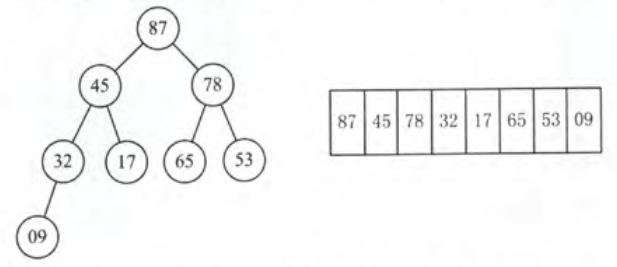

2. 堆排序思路

首先将存放在L[1..n]中的n个元素建成初始堆，由于堆本身的特点（以大顶堆为例），堆顶元素就是最大值。输出堆顶元素后，通常将堆底元素送入堆顶（将堆的最后一个元素与堆顶元素交换，然后数组长度-1，表示删除了输出的元素），此时根结点已不满足大顶堆的性质，堆被破坏，将堆顶元素向下调整使其继续保持大顶堆的性质，再输出堆顶元素。如此重复，直到堆中仅剩一个元素为止。

可见堆排序需要解决两个问题：

如何将无序序列构造成初始堆？
输出堆顶元素后，如何将剩余元素调整成新的堆？

3. 构造初始堆

堆排序的关键是构造初始堆，对初始序列建堆，就是一个反复筛选的过程。

n个结点的完全二叉树，最后一个结点是第L[n/2]（默认下取整）个结点的孩子。对第L[n/2]个结点为根的子树筛选（对于大根堆：
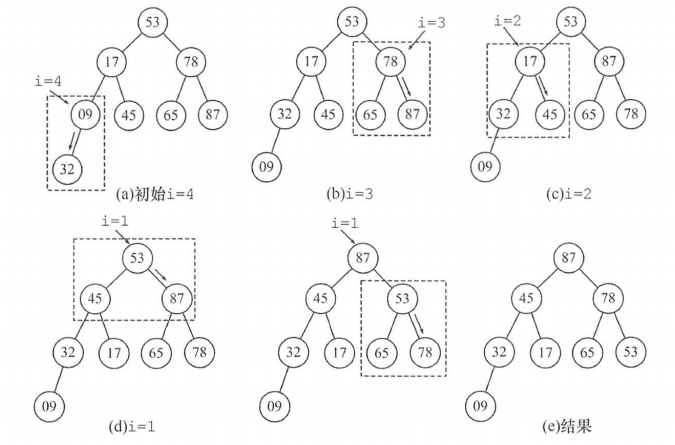
若根结点的关键字小于左右子女中关键字较大者，则交换），使该子树成为堆。之后向前依次对各结点（L[n/2]-1~1）为根的子树进行筛选，看该结点值是否大于其左右子结点的值，若不是，将左右子结点中较大值与之交换，交换后可能会破坏下一级的堆，于是继续采用上述方法构造下一级的堆，直到以该结点为根的子树构成堆为止。反复利用上述调整堆的方法建堆，直到根结点，调整过程的示例如图所示，自上而下调整为大顶堆。

简而言之，就是从最后一棵子树开始，将每棵子树都调整为大顶堆。

初始时调整L（4）子树，09<32，交换，交换后满足堆的定义；
向前继续调整L（3）子树，78<左右孩子的较大者87，交换，交换后满足堆的定义；
向前调整L（2）子树，17<左右孩子的较大者45，交换后满足堆的定义；
向前调整至根结点L（1），53<左右孩子的较大者87，交换，交换后破坏了L（3）子树的堆，采用上述方法对L（3）进行调整，53<左右孩子的较大者78，交换，至此该完全二叉树满足堆的定义。

4. 调整新堆

输出堆顶元素后，将堆的最后一个元素与堆顶元素交换，此时堆的性质被破坏，需要向下进行筛选。

将09和左右孩子的较大者78交换，交换后破坏了L（3）子树的堆，继续对L（3）子树向下筛选，将09和左右孩子的较大者65交换，交换后得到了新堆，调整过程如图所示。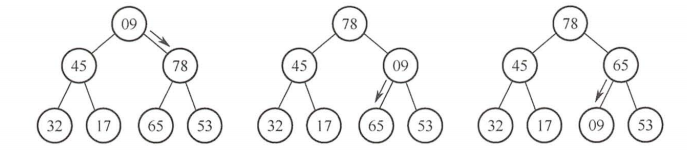

5.代码

c++带哨兵版本

// 调整新堆
void HeadAdjust(vector<int> &a, int k, int len){
    //函数 HeadAdjust 将以元素a[k]为根的子树进行调整
    a[0] = a[k];  // 哨兵暂存子树根结点
    for(int i = 2 * k; i <= len; i *= 2){
        if(i + 1 <= len && a[i] < a[i+1])
            i++;  //取 key 较大的子结点的下标，即右孩子
        if(a[0] < a[i]){
            a[k] = a[i];   //将 a[i]调整到双亲结点上修改
            k = i;  //修改k值以便继续向下筛选
        }
        else    break;  //筛选结束
        a[k] = a[0];
    }
}
// 构造初始大顶堆
void BuildMaxHeap(vector<int>& a, int len){
    for(int i = len / 2; i >= 1; --i){  //从 i=[n/2]~1,反复调整堆  i == 0是哨兵，所以不取
        HeadAdjust(a, i, len);
    }
}
// 堆排序
void HeapSort(vector<int>& a, int len){
    BuildMaxHeap(a, len);
    for(int i = len; i >= 1; --i){
        cout<<a[1]<<" ";
        swap(a[i], a[1]);
        HeadAdjust(a, 1, i-1);
    }
}
int main() {
    vector<int> a = {0,1,3,2,4,5,3,6,7,8,9,7,10,2,11,3,55};  // 第一个是哨兵
    HeapSort(a, a.size()-1);
}

调整的时间与树高有关，为O(h)。在建含n个元素的堆时，关键字的比较总数不超过4n，时间复杂度为O(n)，这说明可以在线性时间内将一个无序数组建成一个堆。

c++无哨兵版本

无哨兵则数组下标从0开始，一个根节点下标和它的左子树下标关系为 2 * root_index + 1 = left_index ，所以边界处理不如带哨兵的方便，但思路都是完全一致的。

// 调整新堆
void HeadAdjust(vector<int> &a, int k, int len){
    //函数 HeadAdjust 将以元素a[k]为根的子树进行调整
    int temp = a[k];  // 哨兵暂存子树根结点
    for(int i = 2 * k + 1; i < len; i = 2*i + 1){
        if(i + 1 < len && a[i] < a[i+1])
            i++;  //取 key 较大的子结点的下标，即右孩子
        if(temp < a[i]){
            a[k] = a[i];   //将 a[i]调整到双亲结点上修改
            k = i;  //修改k值以便继续向下筛选
        }
        else    break;  //筛选结束
    }
    a[k] = temp;
}
// 构造初始大顶堆
void BuildMaxHeap(vector<int>& a, int len){
    for(int i = len / 2 - 1; i >= 0; --i){  //从 i=[n/2]~1,反复调整堆
        HeadAdjust(a, i, len);
    }
}
// 堆排序
void HeapSort(vector<int>& a, int len){
    BuildMaxHeap(a, len);
    for(int i = len - 1; i >= 0; --i){
        cout<<a[0]<<" ";
        swap(a[i], a[0]);
        HeadAdjust(a, 0, i);
    }
}
int main() {
    vector<int> a = {1,3,2,4,5,3,6,7}; 
    HeapSort(a, a.size());
}

6. 堆的插入

堆排序也支持插入操作，对堆进行插入操作时，先将新元素放在末端，然后沿着这棵树进行向上调整的操作。
headAdjust()函数为向下调整，插入要写一个向上调整的函数，与headAdjust()几乎类似，读者可自行实现。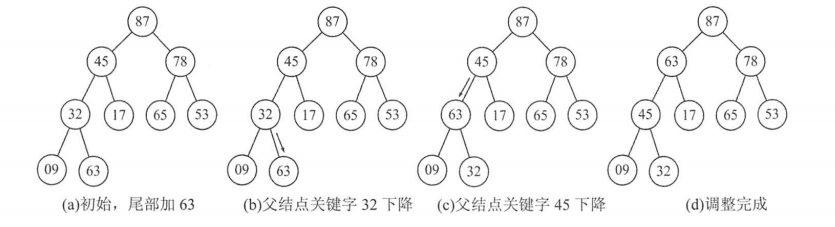

c++无哨兵版本

HeapInsert函数即为插入函数

// 调整新堆
void HeadAdjust(vector<int> &a, int k, int len){
    //函数 HeadAdjust 将以元素a[k]为根的子树进行调整
    int temp = a[k];  // 哨兵暂存子树根结点
    for(int i = 2 * k + 1; i < len; i = 2*i + 1){
        if(i + 1 < len && a[i] < a[i+1])
            i++;  //取 key 较大的子结点的下标，即右孩子
        if(temp < a[i]){
            a[k] = a[i];   //将 a[i]调整到双亲结点上修改
            k = i;  //修改k值以便继续向下筛选
        }
        else    break;  //筛选结束
    }
    a[k] = temp;
}
// 构造初始大顶堆
void BuildMaxHeap(vector<int>& a, int len){
    for(int i = len / 2 - 1; i >= 0; --i){  //从 i=[n/2]~1,反复调整堆
        HeadAdjust(a, i, len);
    }
}
//新增插入函数
void HeapInsert(vector<int>& a, int num){
    a.push_back(num);
    int len = a.size();
    int k = len - 1, temp = a[k];
    // 沿最后一个插入的叶子节点，上溯调整直到根节点
    // 注意子节点和父节点的下标关系，这里用上取整ceil实现
    for(int i = int(ceil(len / 2.0)) - 1; i >= 0; i = int(ceil(i / 2.0)) - 1){ 
        if(temp > a[i]){
            a[k] = a[i];
            k = i;
        }
        else    break;
    }
    a[k] = temp;
}
int main() {
    vector<int> a = {1,3,2,4,5,3,6,7}; 
    BuildMaxHeap(a, a.size()); // 获得大顶堆
    // 插入一个元素并保持大顶堆性质不变
    int num = 6;
    HeapInsert(a, num);  // 插入元素并使数组仍为大顶堆
    for(int i = a.size() - 1; i >= 0; --i){  //输出大顶堆
        cout<<a[0]<<" ";
        swap(a[i], a[0]);
        HeadAdjust(a, 0, i);
    }
}

7. 堆排序性能

空间效率：仅使用了常数个辅助单元，所以空间复杂度为O（1）

时间效率：建堆时间为O(n)，之后有n-1次向下调整操作，每次调整的时间复杂度为O(h))，故在最好、最坏和平均情况下，堆排序的时间复杂度为O（nlogn）

稳定性：进行筛选时，有可能把后面相同关键字的元素调整到前面，所以堆排序算法是一种不稳定的排序方法。例如，表L={1, 2, 2}，构造初始堆时可能将2交换到堆顶，此时L={2, 1, 2}，最终排序序列为L={1, 2, 2}，显然，2与2的相对次序已发生变化。

LeetCode题解与算法

堆排序详解及代码

1. 堆的定义

2. 堆排序思路

3. 构造初始堆

4. 调整新堆

5.代码

c++带哨兵版本

c++无哨兵版本

6. 堆的插入

c++无哨兵版本

7. 堆排序性能