原题地址

0801.png0802.png

方法一 暴力（超时）

思路

最笨的方法就是暴力求解，不过超时，可以不看该解法

暴力求解就是递归，把所有情况都走一遍

我们首先根据起始点从小到大排序，然后我们递归函数 erase_overlap_intervals，它使用上一个区间下标prev和当前区间下标cur作为参数，返回从当前下标开始需要移除的区间个数。

我们从prev=-1 和cur=0开始。在每次递归调用中，检测当前的区间是否与上一个区间重叠。

若不重叠，则不将当前区间从最终列表中移除，以 prev=cur和 cur=cur + 1调用函数erase_overlap_intervals。函数调用的结果存储在 taken变量中。

另一方面，我们也将当前区间移除调用递归，因为本区间可能和后面的区间重叠，因此移除本区间可能会导致更少的区间移除。于是，参数为 prev=prev和 cur=cur + 1。由于我们移除了一个区间，最后的结果应该是函数的返回值再加上 1，存储在 notTaken 变量中。当返回某个特定下标对应的移除数时，返回 taken 和 notTaken 中的较小值。

python代码

  1. def eraseOverlapIntervals(self, intervals: List[List[int]]) -> int:
  2.     intervals = sorted(intervals, key=lambda x: x[0])
  3.     n = len(intervals)
  5.     def erase_overlap_internals(pre, cur):
  6.         if cur == n:
  7.             return 0
  8.         token = 2147483647
  9.         if pre == -1 or (intervals[pre][1] <= intervals[cur][0]):
  10.             token = erase_overlap_internals(cur, cur+1)
  11.         notoken = erase_overlap_internals(pre, cur+1) + 1
  12.         return min(token, notoken)
  14.     return erase_overlap_internals(-1, 0)

时间复杂度O(2^n)

空间复杂度O(n)

方法二 从起始点的动态规划

思路

如果将数组进行排序后，其实大大简化了本题。

这里我们按照起始点从小到大进行排序，然后采用动态规划的思路。

定义dp[i]，表示以下标为i的那个区间结尾的，最大可能的区间数

比如，internals = [[1,2], [2,3]]，则以0下标为结尾的区间只有它本身，也就是[1,2]，所以dp[0]=1，而以1下标为结尾的区间最大有[1,2], [2,3]两个，所以dp[1]=2

同时我们要注意，由于区间之间不能重叠，所以dp[i]的值，不止和dp[i-1]有关，而是和i之前的所有数组有关，因为都有可能重叠，所以我们在求dp[i]时，要遍历之前的所有区间来进行判断。

动规公式：dp[i] = max(dp[j]) + 1, (0<=j<i)

当然啦，按照结束点从小到大排序也是一样的（亲测有效）

python代码

  1. def eraseOverlapIntervals(self, intervals: List[List[int]]) -> int:
  2.     intervals = sorted(intervals, key=lambda x: x[0])
  3.     n = len(intervals)
  4.     dp = [1] * n
  5.     maxSequence = 0
  6.     for i in range(n):  # 计算dp[i]
  7.         temp = 0
  8.         # i之前的所有区间中，找出和i区间不重叠且dp值最大的那个
  9.         for j in range(i):
  10.             if intervals[j][1] <= intervals[i][0] and dp[j] > temp:
  11.                 temp = dp[j]
  12.         dp[i] = temp + 1
  13.         maxSequence = max(maxSequence, dp[i])  # 找出目前为止最长的区间数目
  14.     return n - maxSequence

时间复杂度O(n^2)

空间复杂度O(n)

方法三 从起点的贪心

思路

注：如果按照终点排序，做法是一模一样的，没有任何改变。

先将数组按照起点从小到大排序。

若定义当前指针cur，前一个有效区间的指针pre，这里的有效是指未被删除的区间。

我们遍历一次数组，将当前区间与前一个未删除区间比较，看看当前区间是否应该删除。如果应该删除，则遍历继续，如果不应该删除，则pre指向该区间，遍历继续。

同时在遍历过程中要记录删除区间的个数。

而判断当前区间是否应该删除，则使用贪心算法。下面我们开始分析贪心算法是最优解。

因为数组已经按照起始点排序，所以pre指向的区间和当前区间无非就以下几种情况。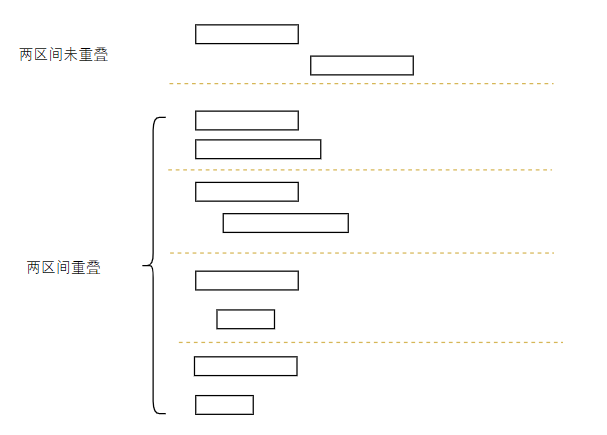0803.png

  • 若未重叠，遍历继续；
  • 若重叠，有两种选择
    1. 不加当前区间，即pre不变
    2. 去掉pre指向的区间，加入当前区间

贪心算法是每次在当前和pre中，选择结束点更小的那一个，这样能给后续选择留有更多的余地。

反证法：假设贪心算法不是最优策略。也就是说每次在当前和pre中，选择结束点更大的那一个是最优策略。那么按照这种策略，后续的选择范围要比贪心策略小，也就是说贪心策略比最优策略更好，矛盾。所以贪心策略是最优解。
举例：[[1,2],[2,3],[2,5],[3,4]]

当pre指向[2,3]，当前区间为[2,5]时，按照贪心策略要不加当前区间，即pre不变，这样能够后续选择留有更多余地。

python代码

  1. def eraseOverlapIntervals(self, intervals: List[List[int]]) -> int:
  2.     intervals = sorted(intervals, key=lambda x: x[0])
  3.     n = len(intervals)
  4.     rel = pre = 0
  5.     for i in range(1, n):
  6.         if intervals[i][0] >= intervals[pre][1]: #不重叠，更新pre
  7.             pre = i
  8.         else:  # 重叠
  9.             if intervals[i][1] > intervals[pre][1]:  # 删掉当前区间
  10.                 rel += 1
  11.             else:  # 删掉pre指向的区间，然后更新pre
  12.                 pre = i
  13.                 rel += 1
  14.     return rel

时间复杂度O(nlogn)

空间复杂度O(1)