207. 课程表

  1. class Solution {
  2.     public boolean canFinish(int numCourses, int[][] prerequisites) {
  3.         //map用来保存每个课程的入度，先完成1才能完成2的话，2的入度是1,1的入度是0
  4.         Map<Integer,Integer> map=new HashMap<>();
  5.         for(int i=0;i<numCourses;i++){
  6.             map.put(i,0);
  7.         }
  8.         //保存一个path记录，比如先完成2才能完成34     2->3、4
  9.         Map<Integer, List<Integer>>path=new HashMap<>();
  10.         for (int[] prerequisite : prerequisites) {
  11.             int pre=prerequisite[1];
  12.             int next=prerequisite[0];
  13.             map.put(next,map.getOrDefault(next,0)+1);
  14.             if(!path.containsKey(pre)) {
  15.                 path.put(pre, new ArrayList<>());
  16.             }
  17.             path.get(pre).add(next);
  18.         }
  19.         //将入度为0的课程入队列
  20.         Deque<Integer>queue=new LinkedList<>();
  21.         for (Integer integer : map.keySet()) {
  22.             if(map.get(integer)==0){
  23.                 queue.addLast(integer);
  24.             }
  25.         }
  26.         while (!queue.isEmpty()){
  27.             int pre=queue.poll();
  28.             if(!path.containsKey(pre)){
  29.                 continue;
  30.             }
  31.             for (Integer integer : path.get(pre)) {
  32.                 //将课程的入度-1,
  33.                 map.put(integer,map.getOrDefault(integer,0)-1);
  34.                 if(map.get(integer)==0){
  35.                     //如果该课程的入度为0，就添加到队列中
  36.                     queue.addLast(integer);
  37.                 }
  38.             }
  39.         }
  40.         for (Integer integer : map.keySet()) {
  41.             //如果map中还有入度>0的课程，就表示不能完成所有的课程
  42.             if(map.get(integer)>0){
  43.                 return false;
  44.             }
  45.         }
  46.         return true;
  47.     }
  48. }

399. 除法求值

  1.     //弗洛伊德算法
  2.     public double[] calcEquation(List<List<String>> equations, double[] values, List<List<String>> queries) {
  3.         double[]res=new double[queries.size()];
  4.         int count=0;
  5.         Map<String, Integer> map = new HashMap<>();
  6.         for (List<String> equation : equations) {
  7.             String a = equation.get(0);
  8.             String b = equation.get(1);
  9.             if(!map.containsKey(a)){
  10.                 map.put(a,count++);
  11.             }
  12.             if(!map.containsKey(b)){
  13.                 map.put(b,count++);
  14.             }
  15.         }
  16.         //构建二维的graph，用来存储变量之间的除法取值
  17.         double[][]graph=new double[count][count];
  18.         for(int i=0;i<count;i++){
  19.             graph[i][i]=1;
  20.         }
  21.         int index=0;
  22.         for (List<String> equation : equations) {
  23.             String a = equation.get(0);
  24.             String b = equation.get(1);
  25.             int aa = map.get(a);
  26.             int bb = map.get(b);
  27.             graph[aa][bb]=values[index];
  28.             graph[bb][aa]=1/values[index];
  29.             index++;
  30.         }
  31.         //弗洛伊德算法求解所有可能
  32.         for(int i=0;i<count;i++){
  33.             for(int j=0;j<count;j++){
  34.                 for(int k=0;k<count;k++){
  35.                     if(graph[j][i]>0&&graph[i][k]>0) {
  36.                         graph[j][k] = graph[j][i] * graph[i][k];
  37.                     }
  38.                 }
  39.             }
  40.         }
  41.         index=0;
  42.         for (List<String> query : queries) {
  43.             String a = query.get(0);
  44.             String b = query.get(1);
  45.             if(map.containsKey(a)&&map.containsKey(b)){
  46.                 int aa=map.get(a);
  47.                 int bb=map.get(b);
  48.                 res[index++]=graph[aa][bb]==0?-1.0:graph[aa][bb];
  49.             }else{
  50.                 res[index++]=-1.0;
  51.             }
  52.         }
  53.         return res;
  54.     }
  55. }

547. 省份数量

  1. //简单并查集的套路，合并就完事了。最后的size表示最终能够分成多少个区域
  2. class Solution {
  3.     public int findCircleNum(int[][] isConnected) {
  4.         int n=isConnected.length;
  5.         UnionFind uf = new UnionFind(n);
  6.         for(int i=0;i<n;i++){
  7.             for(int j=i+1;j<n;j++){
  8.                 if(isConnected[i][j]==1){
  9.                     uf.union(i,j);
  10.                 }
  11.             }
  12.         }
  13.         return uf.size;
  14.     }
  15.     class UnionFind{
  16.         int[] parent;
  17.         int size;
  18.         public UnionFind(int size) {
  19.             this.parent = new int[size];
  20.             for(int i=0;i<parent.length;i++){
  21.                 parent[i]=i;
  22.             }
  23.             this.size=size;
  24.         }
  25.         public int findFather(int x){
  26.             if(x==parent[x]){
  27.                 return x;
  28.             }else{
  29.                 return findFather(parent[x]);
  30.             }
  31.         }
  32.         public void union(int x,int y){
  33.             int fatherX=findFather(x);
  34.             int fatherY=findFather(y);
  35.             if(fatherX!=fatherY){
  36.                 parent[fatherY]=fatherX;
  37.                 size--;
  38.             }
  39.         }
  40.     }
  41. }

684. 冗余连接

  1. //也是简单的并查集套路，如果无法union，就代表这条边重复
  2. class Solution {
  3.     public int[] findRedundantConnection(int[][] edges) {
  4.         int n=edges.length;
  5.         UnionFind uf = new UnionFind(n + 1);
  6.         for (int[] edge : edges) {
  7.             int x=edge[0];
  8.             int y=edge[1];
  9.             if(uf.union(x,y)==null){
  10.                 return new int[]{x,y};
  11.             }
  12.         }
  13.         return null;
  14.     }
  15.     class UnionFind{
  16.         int[]parent;
  17.         int size;
  18.         public UnionFind(int size) {
  19.             this.parent = new int[size];
  20.             for(int i=0;i<size;i++){
  21.                 parent[i]=i;
  22.             }
  23.             this.size=size;
  24.         }
  25.         public int findFather(int x){
  26.             if(x==parent[x]){
  27.                 return x;
  28.             }else{
  29.                 return findFather(parent[x]);
  30.             }
  31.         }
  32.         public int[] union(int x,int y){
  33.             int fatherX = findFather(x);
  34.             int fatherY = findFather(y);
  35.             if(fatherX!=fatherY){
  36.                 if(fatherX<fatherY){
  37.                     parent[fatherY]=fatherX;
  38.                     return new int[]{fatherX,fatherY};
  39.                 }else{
  40.                     parent[fatherX]=fatherY;
  41.                     return new int[]{fatherY,fatherX};
  42.                 }
  43.             }else{
  44.                 return null;
  45.             }
  46.         }
  47.     }
  48. }

778. 水位上升的泳池中游泳

  1. //优先级队列
  2. class Solution {
  3.     public int swimInWater(int[][] grid) {
  4.         PriorityQueue<Node> queue=new PriorityQueue<>(new Comparator<Node>() {
  5.             @Override
  6.             public int compare(Node o1, Node o2) {
  7.                 return o1.val-o2.val;
  8.             }
  9.         });
  10.         int row=grid.length;
  11.         int col=grid[0].length;
  12.         //构建已访问坐标的二维图形
  13.         boolean[][]vis=new boolean[row][col];
  14.         Node root = new Node(0, 0, grid[0][0]);
  15.         queue.add(root);
  16.         int res=root.val;
  17.         int[][]direction=new int[][]{{0,1},{1,0},{0,-1},{-1,0}};
  18.         while (!queue.isEmpty()){
  19.             Node node = queue.poll();
  20.             int i=node.i;
  21.             int j=node.j;
  22.             if(vis[i][j]){
  23.                 continue;
  24.             }
  25.             vis[i][j]=true;
  26.             res=Math.max(node.val,res);
  27.             //如果已到达终点就停止遍历
  28.             if(i==row-1&&j==col-1){
  29.                 break;
  30.             }
  31.             //从上下左右四个方向中去加入坐标进队列中
  32.             for (int[] ints : direction) {
  33.                 int newI=i+ints[0];
  34.                 int newJ=j+ints[1];
  35.                 if(newI>=0&&newI<row&&newJ>=0&&newJ<col&&!vis[newI][newJ]){
  36.                     queue.add(new Node(newI,newJ,grid[newI][newJ]));
  37.                 }
  38.             }
  39.         }
  40.         return res;
  41.     }
  42.     class Node{
  43.         int i;
  44.         int j;
  45.         int val;
  46.         public Node(int i, int j, int val) {
  47.             this.i = i;
  48.             this.j = j;
  49.             this.val = val;
  50.         }
  51.     }
  52. }

839. 相似字符串组

  1. //简单并查集套路
  2. class Solution {
  3.     public int numSimilarGroups(String[] strs) {
  4.         int n=strs.length;
  5.         UnionFind uf = new UnionFind(n);
  6.         for(int i=0;i<n;i++){
  7.             for(int j=i+1;j<n;j++){
  8.                 if(check(strs[i],strs[j])){
  9.                     uf.union(i,j);
  10.                 }
  11.             }
  12.         }
  13.         return uf.size;
  14.     }
  15.     //如果相似则能合并，否则不能合并
  16.     private boolean check(String a,String b){
  17.         int count=0;
  18.         for(int i=0;i<a.length();i++){
  19.             if(a.charAt(i)!=b.charAt(i)){
  20.                 count++;
  21.             }
  22.             if(count>2){
  23.                 return false;
  24.             }
  25.         }
  26.         return true;
  27.     }
  28.     class UnionFind{
  29.         int[]parent;
  30.         int size;
  31.         public UnionFind(int size) {
  32.             this.size = size;
  33.             parent=new int[size];
  34.             for(int i=0;i<size;i++){
  35.                parent[i]=i;
  36.             }
  37.         }
  38.         public int findFather(int x){
  39.             if(x==parent[x]){
  40.                 return x;
  41.             }else{
  42.                 return findFather(parent[x]);
  43.             }
  44.         }
  45.         public void union(int x,int y){
  46.             int fatherX = findFather(x);
  47.             int fatherY = findFather(y);
  48.             if(fatherX!=fatherY){
  49.                 if(fatherX<fatherY){
  50.                     parent[fatherY]=fatherX;
  51.                 }else{
  52.                     parent[fatherX]=fatherY;
  53.                 }
  54.                 size--;
  55.             }
  56.         }
  57.     }
  58. }

947. 移除最多的同行或同列石头

  1. class Solution {
  2.     public int removeStones(int[][] stones) {
  3.         int n=stones.length;
  4.         UnionFind uf = new UnionFind(n);
  5.         for(int i=0;i<stones.length;i++){
  6.             for(int j=i+1;j<stones.length;j++){
  7.                 if(check(stones[i],stones[j])){
  8.                     uf.union(i,j);
  9.                 }
  10.             }
  11.         }
  12.         //最终返回移除了多少块石头
  13.         return n-uf.size;
  14.     }
  15.     //如果同行或者同列，则能合并
  16.     private boolean check(int[]a,int[]b){
  17.         if(a[0]==b[0]||a[1]==b[1]){
  18.             return true;
  19.         }
  20.         return false;
  21.     }
  22.     class UnionFind{
  23.         int[]parent;
  24.         int size;
  25.         public UnionFind(int size) {
  26.             this.size = size;
  27.             parent=new int[size];
  28.             for(int i=0;i<size;i++){
  29.                 parent[i]=i;
  30.             }
  31.         }
  32.         public int findFather(int x){
  33.             if(x==parent[x]){
  34.                 return x;
  35.             }else{
  36.                 return findFather(parent[x]);
  37.             }
  38.         }
  39.         public void union(int x,int y){
  40.             int fatherX = findFather(x);
  41.             int fatherY = findFather(y);
  42.             if(fatherX!=fatherY){
  43.                 if(fatherX<fatherY){
  44.                     parent[fatherY]=fatherX;
  45.                 }else{
  46.                     parent[fatherX]=fatherY;
  47.                 }
  48.                 size--;
  49.             }
  50.         }
  51.     }
  52. }

959. 由斜杠划分区域

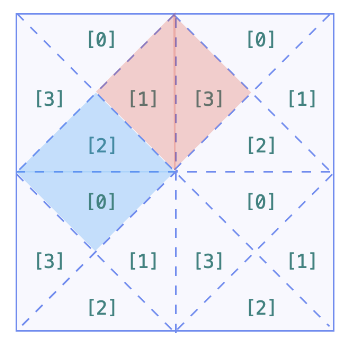
image.png

  1. //这道题有点难度，需要拆分成4个区域来做
  2. class Solution {
  3.     public int regionsBySlashes(String[] grid) {
  4.         int n=grid.length;
  5.         UnionFind uf = new UnionFind(n*n*4);
  6.         for(int i=0;i<n;i++){
  7.             char[] chars = grid[i].toCharArray();
  8.             for(int j=0;j<n;j++){
  9.                 //index标识该区域的首区，比如0、4、8、12
  10.                 int index=4*(n*i+j);
  11.                 if(chars[j]=='/'){
  12.                     //如果是/，合并0、3区域以及1、2区域
  13.                     uf.union(index,index+3);
  14.                     uf.union(index+1,index+2);
  15.                 }else if(chars[j]=='\\'){
  16.                     //如果是\\，合并0、1区域以及2、3区域
  17.                     uf.union(index,index+1);
  18.                     uf.union(index+2,index+3);
  19.                 }else{
  20.                     //如果是空格，合并所有区域
  21.                     uf.union(index,index+1);
  22.                     uf.union(index+1,index+2);
  23.                     uf.union(index+2,index+3);
  24.                 }
  25.                 if(j+1<n){
  26.                     //如果j+1<n，需要合并1、7区域
  27.                     uf.union(index+1,4*(n*i+j+1)+3);
  28.                 }
  29.                 if(i+1<n){
  30.                      //如果i+1<n，需要合并2、8区域
  31.                     uf.union(index+2,4*(n*(i+1)+j));
  32.                 }
  33.             }
  34.         }
  35.         return uf.size;
  36.     }
  37.     class UnionFind{
  38.         int[]parent;
  39.         int size;
  40.         public UnionFind(int size) {
  41.             this.size = size;
  42.             parent=new int[size];
  43.             for(int i=0;i<size;i++){
  44.                 parent[i]=i;
  45.             }
  46.         }
  47.         public int findFather(int x){
  48.             if(x==parent[x]){
  49.                 return x;
  50.             }else{
  51.                 return findFather(parent[x]);
  52.             }
  53.         }
  54.         public void union(int x,int y){
  55.             int fatherX = findFather(x);
  56.             int fatherY = findFather(y);
  57.             if(fatherX!=fatherY){
  58.                 if(fatherX<fatherY){
  59.                     parent[fatherY]=fatherX;
  60.                 }else{
  61.                     parent[fatherX]=fatherY;
  62.                 }
  63.                 size--;
  64.             }
  65.         }
  66.     }
  67. }

1202. 交换字符串中的元素

  1. class Solution {
  2.     public String smallestStringWithSwaps(String s, List<List<Integer>> pairs) {
  3.         int n=s.length();
  4.         UnionFind uf = new UnionFind(n);
  5.         for (List<Integer> pair : pairs) {
  6.             int a=pair.get(0);
  7.             int b=pair.get(1);
  8.             //合并区域
  9.             uf.union(a,b);
  10.         }
  11.         //构建优先级队列
  12.         Map<Integer, PriorityQueue<Character>> map=new HashMap<>();
  13.         for(int i=0;i<s.length();i++){
  14.             int father = uf.findFather(i);
  15.             if(!map.containsKey(father)){
  16.                 map.put(father,new PriorityQueue<>());
  17.             }
  18.             //向优先级队列中添加字符
  19.             map.get(father).add(s.charAt(i));
  20.         }
  21.         StringBuilder builder = new StringBuilder();
  22.         for(int i=0;i<s.length();i++){
  23.             int father = uf.findFather(i);
  24.             //从优先级队列中取出最小值来
  25.             builder.append(map.get(father).poll());
  26.         }
  27.         return builder.toString();
  28.     }
  29.     class UnionFind{
  30.         int[]parent;
  31.         int size;
  32.         public UnionFind(int size) {
  33.             this.size = size;
  34.             parent=new int[size];
  35.             for(int i=0;i<size;i++){
  36.                 parent[i]=i;
  37.             }
  38.         }
  39.         public int findFather(int x){
  40.             if(x==parent[x]){
  41.                 return x;
  42.             }else{
  43.                 return findFather(parent[x]);
  44.             }
  45.         }
  46.         public void union(int x,int y){
  47.             int fatherX = findFather(x);
  48.             int fatherY = findFather(y);
  49.             if(fatherX!=fatherY){
  50.                 if(fatherX<fatherY){
  51.                     parent[fatherY]=fatherX;
  52.                 }else{
  53.                     parent[fatherX]=fatherY;
  54.                 }
  55.             }
  56.         }
  57.     }
  58. }

1319. 连通网络的操作次数

  1. class Solution {
  2.     public int makeConnected(int n, int[][] connections) {
  3.         if(connections.length+1<n){
  4.             return -1;
  5.         }
  6.         UnionFind uf = new UnionFind(n);
  7.         for (int[] connection : connections) {
  8.             int computeA=connection[0];
  9.             int computeB=connection[1];
  10.             uf.union(computeA,computeB);
  11.         }
  12.         return uf.size-1;
  13.     }
  14.     class UnionFind{
  15.         int[]parent;
  16.         int size;
  17.         public UnionFind(int size) {
  18.             parent=new int[size];
  19.             this.size = size;
  20.             for(int i=0;i<size;i++){
  21.                 parent[i]=i;
  22.             }
  23.         }
  24.         public int findFather(int x){
  25.             if(x==parent[x]){
  26.                 return x;
  27.             }else{
  28.                 return findFather(parent[x]);
  29.             }
  30.         }
  31.         public void union(int x,int y){
  32.             int fatherX = findFather(x);
  33.             int fatherY = findFather(y);
  34.             if(fatherX!=fatherY){
  35.                 if(fatherX<fatherY){
  36.                     parent[fatherY]=fatherX;
  37.                 }else{
  38.                     parent[fatherX]=fatherY;
  39.                 }
  40.                 size--;
  41.             }
  42.         }
  43.     }
  44. }

1489. 找到最小生成树里的关键边和伪关键边

  1. //这道题挺难的，用克鲁斯卡尔算法。先构建最小生成树，然后再判断是否是伪关键边、关键边
  2. class Solution {
  3.     public List<List<Integer>> findCriticalAndPseudoCriticalEdges(int n, int[][] edges) {
  4.         UnionFind ufMST = new UnionFind(n);
  5.         int count=0;
  6.         Map<int[],Integer> map=new HashMap<>();
  7.         for (int[] edge : edges) {
  8.             //存储边的下标
  9.             map.put(edge,count++);
  10.         }
  11.         //按边的dis进行排序
  12.         Arrays.sort(edges, new Comparator<int[]>() {
  13.             @Override
  14.             public int compare(int[] o1, int[] o2) {
  15.                 return o1[2]-o2[2];
  16.             }
  17.         });
  18.         //最小生成树的边
  19.         List<Integer>mst=new ArrayList<>();
  20.         int minDis=0;
  21.         //构建最小生成树
  22.         for(int i=0;i<edges.length;i++){
  23.             int from=edges[i][0];
  24.             int to=edges[i][1];
  25.             int dis=edges[i][2];
  26.             if(ufMST.union(from,to)){
  27.                minDis+=dis;
  28.                mst.add(i);
  29.             }
  30.         }
  31.         //存储关键边集合
  32.         List<Integer>importantEdge=new ArrayList<>();
  33.         //存储伪关键边集合
  34.         List<Integer>fakeEdge=new ArrayList<>();
  35.         for(int i=0;i<edges.length;i++){
  36.             UnionFind uf = new UnionFind(n);
  37.             int curCount=0;
  38.             int curDis=0;
  39.             //如果mst中不包含这条边，判断它是否是伪关键边
  40.             if(!mst.contains(i)){
  41.                 int from=edges[i][0];
  42.                 int to=edges[i][1];
  43.                 int dis=edges[i][2];
  44.                 uf.union(from,to);
  45.                 curCount++;
  46.                 curDis+=dis;
  47.             }
  48.             //如果mst中包含这条边，判断它是否是关键边
  49.             for(int j=0;j<edges.length;j++){
  50.                 //如果j与i相等的话，则表示当前已在遍历中
  51.                 if(j==i){
  52.                     continue;
  53.                 }
  54.                 int from=edges[j][0];
  55.                 int to=edges[j][1];
  56.                 int dis=edges[j][2];
  57.                 if(uf.union(from,to)){
  58.                     curCount++;
  59.                     curDis+=dis;
  60.                     if(curCount==n-1){
  61.                         break;
  62.                     }
  63.                 }
  64.             }
  65.             if(mst.contains(i)&&(curCount<n-1||curDis>minDis)){
  66.                 importantEdge.add(map.get(edges[i]));
  67.             }else if(curCount==n-1&&curDis==minDis){
  68.                 fakeEdge.add(map.get(edges[i]));
  69.             }
  70.         }
  71.         List<List<Integer>>res=new ArrayList<>();
  72.         res.add(importantEdge);
  73.         res.add(fakeEdge);
  74.         return res;
  75.     }
  76.     class UnionFind{
  77.         int[]parent;
  78.         int[]rank;
  79.         int size;
  80.         public UnionFind(int size) {
  81.             this.size = size;
  82.             parent=new int[size];
  83.             rank=new int[size];
  84.             for(int i=0;i<size;i++){
  85.                 parent[i]=i;
  86.                 rank[i]=1;
  87.             }
  88.         }
  89.         public int findFather(int x){
  90.             if(x==parent[x]){
  91.                 return x;
  92.             }else{
  93.                 return findFather(parent[x]);
  94.             }
  95.         }
  96.         public boolean union(int x,int y){
  97.             int fatherX = findFather(x);
  98.             int fatherY = findFather(y);
  99.             if(fatherX==fatherY){
  100.                 return false;
  101.             }else{
  102.                 if(rank[fatherY]<=rank[fatherX]){
  103.                     parent[fatherY]=fatherX;
  104.                     rank[fatherX]++;
  105.                 }else{
  106.                     parent[fatherX]=fatherY;
  107.                     rank[fatherY]++;
  108.                 }
  109.             }
  110.             return true;
  111.         }
  112.     }
  113. }

1579. 保证图可完全遍历

  1. class Solution {
  2.     public int maxNumEdgesToRemove(int n, int[][] edges) {
  3.         int res=0;
  4.         UnionFind ufAlice = new UnionFind(n + 1);
  5.         UnionFind ufBob = new UnionFind(n + 1);
  6.         //优先Alice和Bob都能遍历的边
  7.         for (int[] edge : edges) {
  8.             int type=edge[0];
  9.             int pointA=edge[1];
  10.             int pointB=edge[2];
  11.             if(type==3){
  12.                 if(ufAlice.isConnected(pointA,pointB)){
  13.                     res++;
  14.                 }else{
  15.                     ufAlice.union(pointA,pointB);
  16.                     ufBob.union(pointA,pointB);
  17.                 }
  18.             }
  19.         }
  20.         for (int[] edge : edges) {
  21.             int type=edge[0];
  22.             int pointA=edge[1];
  23.             int pointB=edge[2];
  24.             if(type==1){
  25.                 if(ufAlice.isConnected(pointA,pointB)){
  26.                     res++;
  27.                 }else{
  28.                     ufAlice.union(pointA,pointB);
  29.                 }
  30.             }else if(type==2){
  31.                 if(ufBob.isConnected(pointA,pointB)){
  32.                     res++;
  33.                 }else{
  34.                     ufBob.union(pointA,pointB);
  35.                 }
  36.             }
  37.         }
  38.         if(ufAlice.size==2&&ufBob.size==2){
  39.             return res;
  40.         }else{
  41.             return -1;
  42.         }
  43.     }
  44.     class UnionFind{
  45.         int[]parent;
  46.         int[]rank;
  47.         int size;
  48.         public UnionFind(int size) {
  49.             this.size = size;
  50.             parent=new int[size];
  51.             rank=new int[size];
  52.             for(int i=0;i<size;i++){
  53.                 parent[i]=i;
  54.                 rank[i]=1;
  55.             }
  56.         }
  57.         public int findFather(int x){
  58.             if(x==parent[x]){
  59.                 return x;
  60.             }else{
  61.                 return findFather(parent[x]);
  62.             }
  63.         }
  64.         public void union(int x,int y){
  65.             int fatherX = findFather(x);
  66.             int fatherY = findFather(y);
  67.             if(fatherX==fatherY){
  68.                 return;
  69.             }
  70.             if(rank[fatherY]<=rank[fatherX]){
  71.                 parent[fatherY]=fatherX;
  72.                 rank[fatherX]++;
  73.             }else if(rank[fatherY]>rank[fatherX]){
  74.                 parent[fatherX]=fatherY;
  75.                 rank[fatherY]++;
  76.             }
  77.             size--;
  78.         }
  79.         public boolean isConnected(int x,int y){
  80.             int fatherX = findFather(x);
  81.             int fatherY = findFather(y);
  82.             if(fatherX==fatherY){
  83.                 return true;
  84.             }else{
  85.                 return false;
  86.             }
  87.         }
  88.     }
  89. }

1584. 连接所有点的最小费用

  1. //普利姆算法
  2. class Solution {
  3.     public int minCostConnectPoints(int[][] points) {
  4.         int n=points.length;
  5.         int[][]graph=new int[n][n];
  6.         for(int i=0;i<n;i++){
  7.             for(int j=i+1;j<n;j++){
  8.                 graph[i][j]=graph[j][i]=Math.abs(points[i][0]-points[j][0])+Math.abs(points[i][1]-points[j][1]);
  9.             }
  10.         }
  11.         //构建优先级队列
  12.         PriorityQueue<Node>queue=new PriorityQueue<>(new Comparator<Node>() {
  13.             @Override
  14.             public int compare(Node o1, Node o2) {
  15.                 if(o1.dis==o2.dis){
  16.                     return o1.val-o2.val;
  17.                 }else{
  18.                     return o1.dis-o2.dis;
  19.                 }
  20.             }
  21.         });
  22.         for(int i=1;i<n;i++){
  23.             queue.add(new Node(i,graph[0][i]));
  24.         }
  25.         int res=0;
  26.         while (!queue.isEmpty()){
  27.             Node node = queue.poll();
  28.             //如果为0表示当前节点已遍历过，或者是a->a为0的这种，就不需要遍历
  29.             if(graph[0][node.val]==0){
  30.                 continue;
  31.             }
  32.             res+=node.dis;
  33.             graph[0][node.val]=0;
  34.             for(int i=0;i<n;i++){
  35.                 //如果在这些节点中找到比当前遍历小的路径，就加入到优先级队列中去
  36.                 if(graph[node.val][0]!=0&&graph[node.val][i]<graph[0][i]){
  37.                     queue.add(new Node(i,graph[node.val][i]));
  38.                     graph[0][i]=graph[node.val][i];
  39.                 }
  40.             }
  41.         }
  42.         return res;
  43.     }
  44.     //用Node节点封装边的长度与索引
  45.     class Node{
  46.         int val;
  47.         int dis;
  48.         public Node(int val, int dis) {
  49.             this.val = val;
  50.             this.dis = dis;
  51.         }
  52.     }
  53. }