双指针，指的是在遍历对象的过程中，不是普通的使用单个指针进行访问，而是使用两个相同方向（快慢指针）或者相反方向（对撞指针）的指针进行扫描，从而达到相应的目的。
换言之，双指针法充分使用了数组有序这一特征，从而在某些情况下能够简化一些运算。
在 LeetCode 题库中，关于双指针的问题还是挺多的。双指针

对撞指针

对撞指针是指在数组中，将指向最左侧的索引定义为左指针(left)，最右侧的定义为右指针(right)，然后从两头向中间进行数组遍历。
—-> * <—-
“夹逼”

对撞数组适用于连续数组和字符串，也就是说当你遇到题目给定连续数组和字符床时，应该第一时间想到用对撞指针解题。

伪代码大致如下：

public void find (int[] list) {
  var left = 0;
  var right = list.length - 1;
  //遍历数组
  while (left <= right) {
    left++;
    // 一些条件判断 和处理
    ... ...
    right--;
  }
}

leetcode344-反转字符串

https://leetcode-cn.com/problems/reverse-string/
编写一个函数，其作用是将输入的字符串反转过来。输入字符串以字符数组 char[] 的形式给出。
不要给另外的数组分配额外的空间，你必须原地修改输入数组、使用 O(1) 的额外空间解决这一问题。
你可以假设数组中的所有字符都是 ASCII 码表中的可打印字符。
示例 1：

输入：["h","e","l","l","o"]
输出：["o","l","l","e","h"]

示例 2：

输入：["H","a","n","n","a","h"]
输出：["h","a","n","n","a","H"]

代码
可以套用前面的伪代码：

class Solution {
    public void reverseString(char[] s) {
        if (s.length == 0 || s.length == 1) return ;
        int left = 0;
        int right = s.length-1;
        while (left <right) {
            char temp = s[left];
            s[left++] = s[right];
            s[right--] = temp;
        }
        return ;
    }
}

复杂度分析
时间复杂度：O(N)，其中 NN 为字符数组的长度。一共执行了 N/2 次的交换。
空间复杂度：O(1)。只使用了常数空间来存放若干变量。

leetcode209-长度最小的子数组

https://leetcode-cn.com/problems/minimum-size-subarray-sum/
给定一个含有 n 个正整数的数组和一个正整数 s ，找出该数组中满足其和 ≥ s 的长度最小的连续子数组，并返回其长度。如果不存在符合条件的子数组，返回 0。

示例：

输入：s = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。

定义两个指针left 和 right 分别表示子数组（滑动窗口窗口）的开始位置和结束位置，维护变量 sum 存储子数组中的元素和（即从 nums[left] 到 nums[right] 的元素和）。
初始状态下，left 和 right 都指向下标 0，sum 的值为 0。

每一轮迭代，将 nums[right] 加到 sum，如果 sum≥s，则更新子数组的最小长度（此时子数组的长度是 right−left+1），然后将 nums[left] 从 sum 中减去并将 left 右移，直到 sum<s，在此过程中同样更新子数组的最小长度。在每一轮迭代的最后，将 right 右移。

代码

class Solution {
    public int minSubArrayLen(int s, int[] nums) {
        int right =0;
        int left=0;
        int sum =0;
        int len =Integer.MAX_VALUE;
        while(right < nums.length) {
            sum+=nums[right];
            while (sum >=s) {
               len = Math.min(right -left+1,len);
               sum -= nums[left]; 
               left++;
            }
            right++;
        }
        if (len == Integer.MAX_VALUE) return 0;
        return len;
    }
}

复杂度分析
时间复杂度：O(n)，其中 n 是数组的长度。指针left 和 right 最多各移动 n 次。
空间复杂度：O(1)。

虽然这道题目也是用的双指针，但是实际上采用滑动窗口的算法思想，具体可以看文章：滑动窗口算法基本原理与实践。

快慢指针

快慢指针也是双指针，但是两个指针从同一侧开始遍历数组，将这两个指针分别定义为快指针（fast）和慢指针（slow），两个指针以不同的策略移动，直到两个指针的值相等（或其他特殊条件）为止，如 fast 每次增长两个，slow 每次增长一个。
—-> —-> *
“争先恐后”

以LeetCode 141.环形链表为例,，判断给定链表中是否存在环，可以定义快慢两个指针，快指针每次增长一个，而慢指针每次增长两个，最后两个指针指向节点的值相等，则说明有环。就好像一个环形跑道上有一快一慢两个运动员赛跑，如果时间足够长，跑地快的运动员一定会赶上慢的运动员。

快慢指针一般都初始化指向链表的头结点 head，前进时快指针 fast 在前，慢指针 slow 在后，巧妙解决一些链表中的问题。

leetcode141-判断是否为环形链表

https://leetcode-cn.com/problems/linked-list-cycle/
这应该属于链表最基本的操作了，如果读者已经知道这个技巧，可以跳过。
单链表的特点是每个节点只知道下一个节点，所以一个指针的话无法判断链表中是否含有环的。
如果链表中不包含环，那么这个指针最终会遇到空指针 null 表示链表到头了，这还好说，可以判断该链表不含环。

boolean hasCycle(ListNode head) {
    while (head != null)
        head = head.next;
    return false;
}

但是如果链表中含有环，那么这个指针就会陷入死循环，因为环形数组中没有 null 指针作为尾部节点。
经典解法就是用两个指针，一个每次前进两步，一个每次前进一步。如果不含有环，跑得快的那个指针最终会遇到 null，说明链表不含环；如果含有环，快指针最终会和慢指针相遇，说明链表含有环。
就好像一个环形跑道上有一快一慢两个运动员赛跑，如果时间足够长，跑地快的运动员一定会赶上慢的运动员。

boolean hasCycle(ListNode head) {
    ListNode fast, slow;
    fast = slow = head;
    while(fast != null && fast.next != null) {
        fast = fast.next.next;
        slow = slow.next;
        if (fast == slow)
            return true;
    }
    return false;
}

复杂度分析
时间复杂度：O(N)，其中 N 是链表中的节点数。

当链表中不存在环时，快指针将先于慢指针到达链表尾部，链表中每个节点至多被访问两次。
当链表中存在环时，每一轮移动后，快慢指针的距离将减小一。而初始距离为环的长度，因此至多移动 NN 轮。

空间复杂度：O(1)。我们只使用了两个指针的额外空间。

leetcode142-已知链表中含有环，返回这个环的起始位置

https://leetcode-cn.com/problems/linked-list-cycle-ii/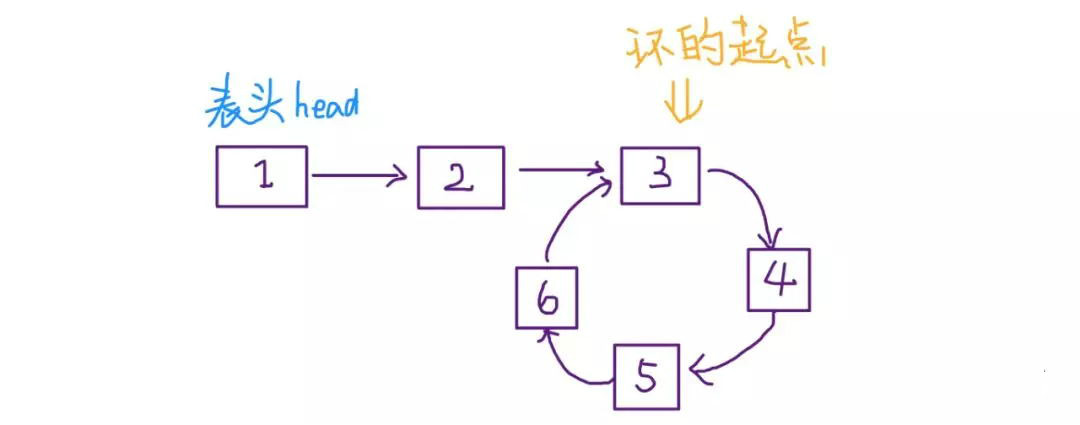

这个问题其实不困难，有点类似脑筋急转弯，先直接看代码：

public ListNode detectCycle(ListNode head) {
    ListNode fast, slow;
    fast = slow = head;
    while (fast != null && fast.next != null) {
        fast = fast.next.next;
        slow = slow.next;
        if (fast == slow)
            break;
    }
    slow = head;
    while (slow != fast) {
        fast = fast.next;
        slow = slow.next;
    }
    return slow;
}

可以看到，当快慢指针相遇时，让其中任一个指针重新指向头节点，然后让它俩以相同速度前进，再次相遇时所在的节点位置就是环开始的位置。

复杂度分析

时间复杂度：O(N)，其中 N 为链表中节点的数目。在最初判断快慢指针是否相遇时，slow 指针走过的距离不会超过链表的总长度；随后寻找入环点时，走过的距离也不会超过链表的总长度。因此，总的执行时间为 O(N)+O(N)=O(N)
空间复杂度：O(1)。我们只使用了 slow,fast,ptr 三个指针。

leetcode876-寻找链表的中点

https://leetcode-cn.com/problems/middle-of-the-linked-list
用两个指针 slow 与 fast 一起遍历链表。slow 一次走一步，fast 一次走两步。那么当 fast 到达链表的末尾时，slow 必然位于中间。

class Solution {
    public ListNode middleNode(ListNode head) {
        ListNode slow = head, fast = head;
        while (fast != null && fast.next != null) {
            slow = slow.next;
            fast = fast.next.next;
        }
        return slow;
    }
}

复杂度分析
时间复杂度：O(N)O(N)，其中 NN 是给定链表的结点数目。
空间复杂度：O(1)O(1)，只需要常数空间存放 slow 和 fast 两个指针。

当链表的长度是奇数时，slow 恰巧停在中点位置；如果长度是偶数，slow 最终的位置是中间偏右：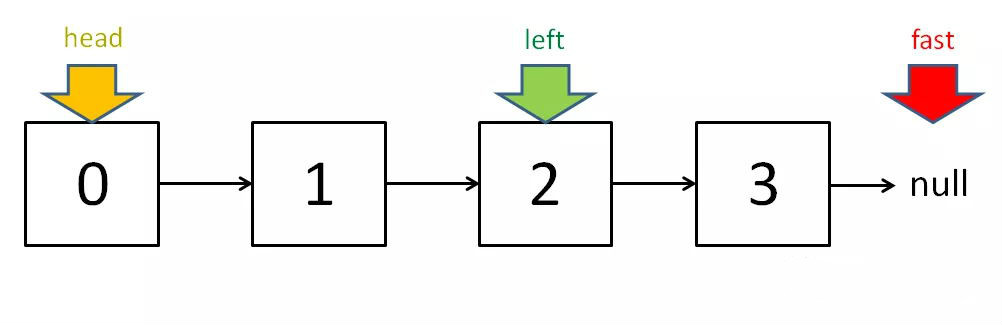

寻找链表中点的一个重要作用是对链表进行归并排序。
回想数组的归并排序：求中点索引递归地把数组二分，最后合并两个有序数组。对于链表，合并两个有序链表是很简单的，难点就在于二分。
但是现在你学会了找到链表的中点，就能实现链表的二分了。

关于归并排序的具体内容本文就不具体展开了。看：归并排序

jzoffer22-寻找链表的倒数第K个元素

https://leetcode-cn.com/problems/lian-biao-zhong-dao-shu-di-kge-jie-dian-lcof/

初始化：前指针 fast 、后指针 slow ，双指针都指向头节点 head 。
构建双指针距离：前指针 fast 先向前走 k 步（结束后，双指针 fast 和 slow 间相距 k 步）。
双指针共同移动：循环中，双指针 fast 和 slow 每轮都向前走一步，直至 fast 走过链表尾节点时跳出（跳出后， slow 与尾节点距离为 k-1，即 slow 指向倒数第 k 个节点）。

返回值：返回 slow 即可。

public ListNode getKthFromEnd(ListNode head, int k) {
      ListNode fast = head, slow = head;
      for(int i = 0; i < k; i++)
          fast = fast.next;
      while(former != null) {
          fast = fast.next;
          slow = slow.next;
      }
      return slow;
  }

复杂度分析：
时间复杂度 O(N) ： N 为链表长度；总体看， fast 走了 N 步， slow 走了 (N−k) 步。
空间复杂度 O(1) ：双指针 fast , slow 使用常数大小的额外空间。

滑动窗口

滑动窗口算法基本原理与实践

刷题记录 || 📝

双指针算法基本原理与实践