题目链接

示例

给你一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 a，b，c ，使得 a + b + c = 0 ？请你找出所有和为 0 且不重复的三元组。
注意：答案中不可以包含重复的三元组。

示例 1：
输入：nums = [-1,0,1,2,-1,-4]
输出：[[-1,-1,2],[-1,0,1]]
示例 2：
输入：nums = []
输出：[]
示例 3：
输入：nums = [0]
输出：[]

解题思路

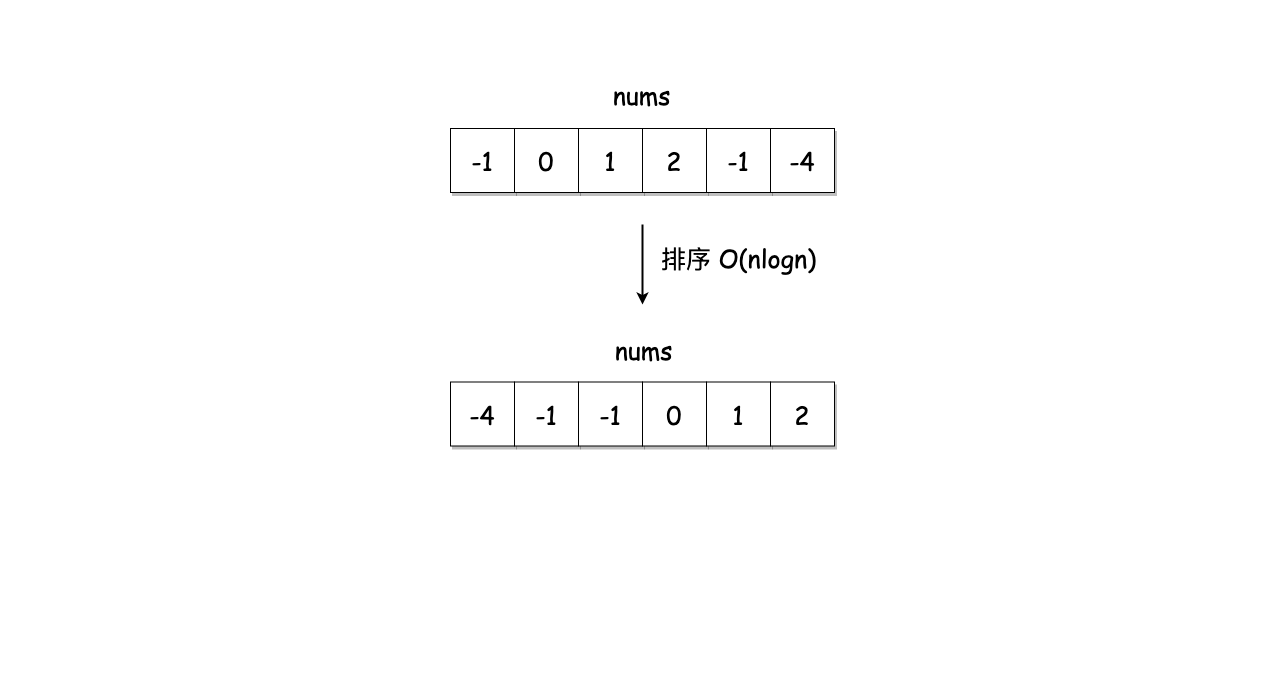
思路：排序 + 双指针
本题的难点在于如何去除重复解。

算法流程：

1. 特判，对于数组长度 n，如果数组为 null 或者数组长度小于 3，返回 []。
2. 对数组进行排序。
3. 遍历排序后数组：
   • 若 nums[i]>0：因为已经排序好，所以后面不可能有三个数加和等于 0，直接返回结果。
   • 对于重复元素：跳过，避免出现重复解
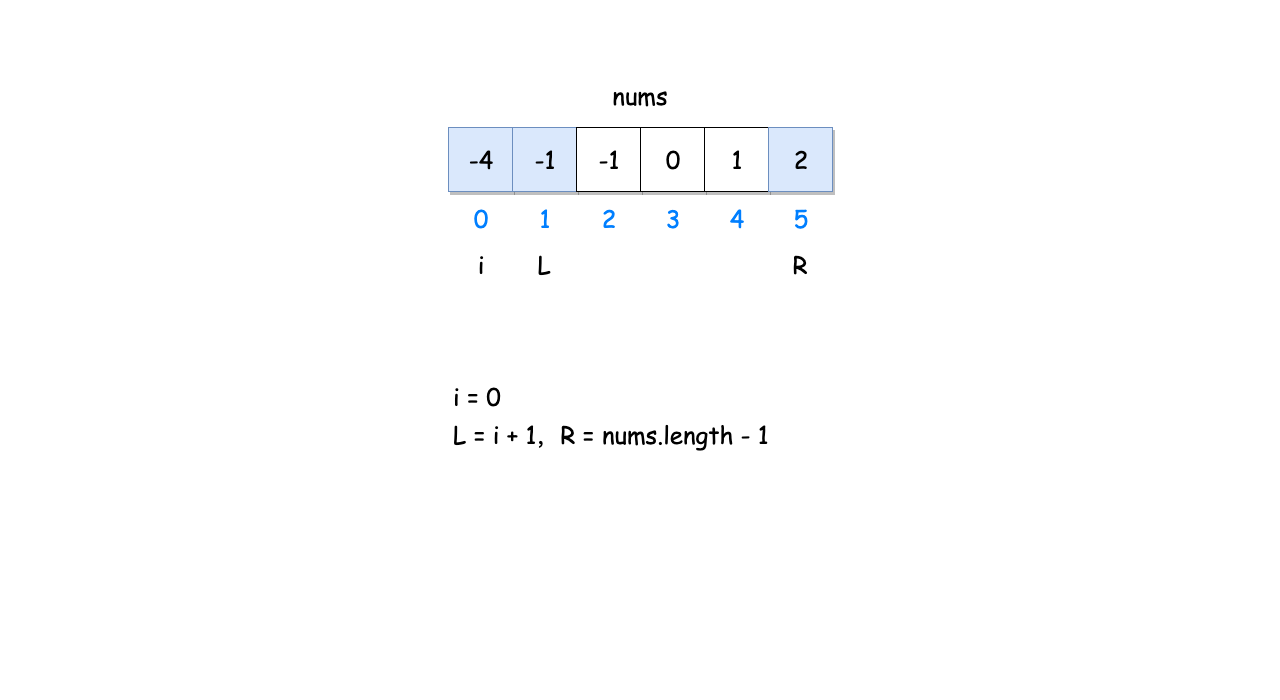
   • 令左指针 L=i+1，右指针 R=n−1，当 L<R 时，执行循环：
     • 当 nums[i]+nums[L]+nums[R]==0，执行循环，判断左界和右界是否和下一位置重复，去除重复解。并同时将 L,R 移到下一位置，寻找新的解
     • 若和大于 0，说明 nums[R] 太大，R 左移
     • 若和小于 0，说明 nums[L] 太小，L 右移

复杂度分析
时间复杂度：O(n2)，数组排序 O(NlogN)，遍历数组 O(n)，双指针遍历 O(n)，总体 O(NlogN)+O(n)∗O(n)，O(n2)
空间复杂度：O(1)

「图解」

代码

public List<List<Integer>> threeSum(int[] nums) {
        List<List<Integer>> lists = new ArrayList<>();
        //排序
        Arrays.sort(nums);
        //双指针
        int len = nums.length;
        for(int i = 0;i < len;++i) {
            if(nums[i] > 0) return lists;
            if(i > 0 && nums[i] == nums[i-1]) continue;
            int curr = nums[i];
            int L = i+1, R = len-1;
            while (L < R) {
                int tmp = curr + nums[L] + nums[R];
                if(tmp == 0) {
                    List<Integer> list = new ArrayList<>();
                    list.add(curr);
                    list.add(nums[L]);
                    list.add(nums[R]);
                    lists.add(list);
                    while(L < R && nums[L+1] == nums[L]) ++L;
                    while (L < R && nums[R-1] == nums[R]) --R;
                    ++L;
                    --R;
                } else if(tmp < 0) {
                    ++L;
                } else {
                    --R;
                }
            }
        }
        return lists;
    }