缘起

最近阅读<<我的第一本算法书>>(【日】石田保辉；宫崎修一)
本系列笔记拟采用golang练习之

欧几里得算法

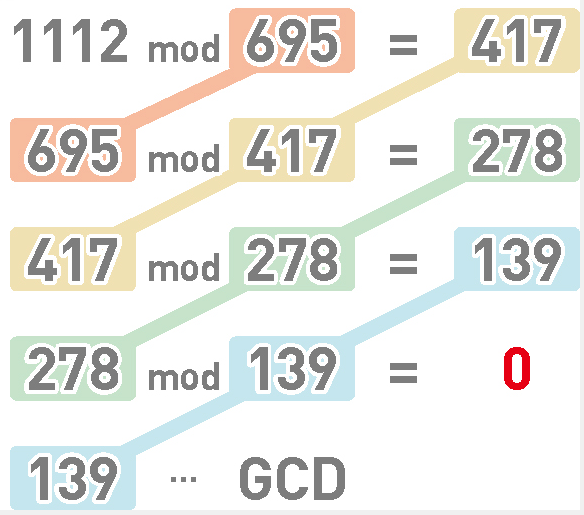
欧几里得算法（又称辗转相除法）用于计算两个数的最大公约数，
被称为世界上最古老的算法。
现在人们已无法确定该算法具体的提出时间，
但其最早被发现记载于公元前300年欧几里得的著作中，
因此得以命名。
首先用较小的数字去除较大的数字，求出余数。
接下来再用较小的除数和余数进行mod运算,
重复同样的操作,
余数为0时，最后一次运算中的除数就是最大公约数。
摘自 <<我的第一本算法书>> 【日】石田保辉；宫崎修一

目标

• 分别用因式分解法和欧几里德算法求解若干随机整数的最大公约数, 并相互验证

设计

• IGCDCalculator: 最大公约数计算器接口
• tEuclideanCalculator: 欧几里德算法实现最大公约数求解
• tNormalGcdCalculator: 因式分解法实现最大公约数求解

单元测试

euclidean_gcd_test.go, 对比验证欧几里德算法和因式分解法, 并比较计算效率

package others
import (
    "learning/gooop/others/euclidean"
    "math/rand"
    "testing"
    "time"
)
func TestEuclideanGCD(t *testing.T) {
    fnAssertTrue := func(b bool, msg string) {
        if !b {
            t.Fatal(msg)
        }
    }
    rnd := rand.New(rand.NewSource(time.Now().UnixNano()))
    sampleCount := 100
    samples := make([]int, sampleCount)
    for i,_ := range samples {
        samples[i] = rnd.Intn(sampleCount) + 1
    }
    fnGenInt := func() int {
        n := rnd.Intn(5) + 1
        x := 1
        for i := 0;i < n;i++ {
            j := rnd.Intn(sampleCount)
            x *= samples[j]
        }
        return x
    }
    c1 := euclidean.EuclideanGCDCalculator
    c2 := euclidean.NormalGCDCalculator
    t.Log("testing 10 samples")
    for i := 0;i < 10;i++ {
        a,b := fnGenInt(), fnGenInt()
        g1 := c1.Calc(a, b)
        g2 := c2.Calc(a, b)
        //t.Logf("a=%v, b=%v, g1=%v, g2=%v", a, b, g1, g2)
        fnAssertTrue(g1 == g2, "expecting g1 == g2")
        fnAssertTrue(a % g1 == 0, "expecting a % gcd == 0")
        fnAssertTrue(b % g1 == 0, "expecting b % gcd == 0")
        t.Logf("gcd(%v, %v) = %v", a, b, g1)
    }
    t.Log("pass testing 10 samples")
    t.Log("\ntesting 100_000 samples")
    for i := 0;i < 100_000;i++ {
        a,b := fnGenInt(), fnGenInt()
        g1 := c1.Calc(a, b)
        g2 := c2.Calc(a, b)
        fnAssertTrue(g1 == g2, "expecting g1 == g2")
        fnAssertTrue(a % g1 == 0, "expecting a % gcd == 0")
        fnAssertTrue(b % g1 == 0, "expecting b % gcd == 0")
    }
    t.Log("pass testing 100_000 samples")
    fnTestCost := func(samples[][] int, c euclidean.IGCDCalculator) int64 {
        t0 := time.Now().UnixNano()
        for i, size := 0, len(samples);i < size;i++ {
            a, b := samples[i][0], samples[i][1]
            g1 := c.Calc(a, b)
            fnAssertTrue(a%g1 == 0, "expecting a % gcd == 0")
            fnAssertTrue(b%g1 == 0, "expecting b % gcd == 0")
        }
        cost := (time.Now().UnixNano() - t0) / 1000_000
        return cost
    }
    pairs := make([][]int, 10_000)
    for i,size := 0, len(pairs);i < size;i++ {
        pairs[i] = []int{ fnGenInt(), fnGenInt() }
    }
    t.Logf("testing 10_000 samples using EuclideanGCDCalculator, cost=%v ms", fnTestCost(pairs, c1))
    t.Logf("testing 10_000 samples using NormalGCDCalculator, cost=%v ms", fnTestCost(pairs, c2))
}

测试输出

显而易见, 欧几里德算法要快上N个数量级

$ go test -v euclidean_gcd_test.go 
=== RUN   TestEuclideanGCD
    euclidean_gcd_test.go:37: testing 10 samples
    euclidean_gcd_test.go:47: gcd(122262, 2135280) = 1722
    euclidean_gcd_test.go:47: gcd(2563600, 180180) = 260
    euclidean_gcd_test.go:47: gcd(5, 2019600) = 5
    euclidean_gcd_test.go:47: gcd(78540, 1547) = 119
    euclidean_gcd_test.go:47: gcd(17476560, 749800800) = 563760
    euclidean_gcd_test.go:47: gcd(395600, 12792) = 8
    euclidean_gcd_test.go:47: gcd(21, 165) = 3
    euclidean_gcd_test.go:47: gcd(7056, 2257) = 1
    euclidean_gcd_test.go:47: gcd(90, 918) = 18
    euclidean_gcd_test.go:47: gcd(90843648, 2522520) = 1176
    euclidean_gcd_test.go:49: pass testing 10 samples
    euclidean_gcd_test.go:51: 
        testing 100_000 samples
    euclidean_gcd_test.go:61: pass testing 100_000 samples
    euclidean_gcd_test.go:80: testing 10_000 samples using EuclideanGCDCalculator, cost=1 ms
    euclidean_gcd_test.go:81: testing 10_000 samples using NormalGCDCalculator, cost=721 ms
--- PASS: TestEuclideanGCD (8.34s)
PASS
ok      command-line-arguments  8.347s

IGCDCalculator.go

最大公约数计算器接口

package euclidean
type IGCDCalculator interface {
    Calc(a, b int) int
}

tEuclideanCalculator.go

欧几里德算法实现最大公约数求解

package euclidean
type tEuclideanCalculator struct {
}
func newEuclideanCalculator() IGCDCalculator {
    return &tEuclideanCalculator{}
}
func (me *tEuclideanCalculator) Calc(a, b int) int {
    if a <= 0 || b <= 0 {
        return 1
    }
    if a == b {
        return a
    }
    bigger := max(a, b)
    smaller := min(a, b)
    for smaller > 0 {
        remaining := bigger % smaller
        if remaining == 0 {
            return smaller
        } else {
            bigger ,smaller = smaller, remaining
        }
    }
    return 1
}
func max(a, b int) int {
    if a >= b {
        return a
    }
    return b
}
func min(a, b int) int {
    if a <= b {
        return a
    }
    return b
}
var EuclideanGCDCalculator = newEuclideanCalculator()

tNormalGcdCalculator.go

因式分解法实现最大公约数求解

package euclidean
import (
    "math"
    "sort"
)
type tNormalGcdCalculator struct {
}
func newNormalGcdCalculator() IGCDCalculator {
    return &tNormalGcdCalculator{}
}
func (me *tNormalGcdCalculator) Calc(a, b int) int {
    if a <= 0 || b <= 0 {
        return 1
    }
    if a == b {
        return a
    }
    aa := me.split(a)
    sort.Sort(sort.IntSlice(aa))
    bb := me.split(b)
    sort.Sort(sort.IntSlice(bb))
    for i, j := len(aa) - 1, len(bb) - 1;i >= 0 && j >= 0; {
        if aa[i] == bb[j] {
            return aa[i]
        }
        if aa[i] > bb[j] {
            i--
        } else {
            j--
        }
    }
    return 1
}
func (me *tNormalGcdCalculator) split(a int) []int {
    to := int(math.Floor(math.Sqrt(float64(a))))
    items := make([]int, 0)
    for i := 1;i <= to;i++ {
        if a % i == 0 {
            items = append(items, i)
            items = append(items, a / i)
        }
    }
    return items
}
var NormalGCDCalculator = newNormalGcdCalculator()

(end)