1. 线索化二叉树
1.1 产生背景
假设我们有一个结点为N的二叉树,当它采用链式存储时,结点下存在两个指针域,分别存储左孩子与右孩子
此时,二叉树一共存在N - 1条有效路径,同时也存在N + 1个空指针域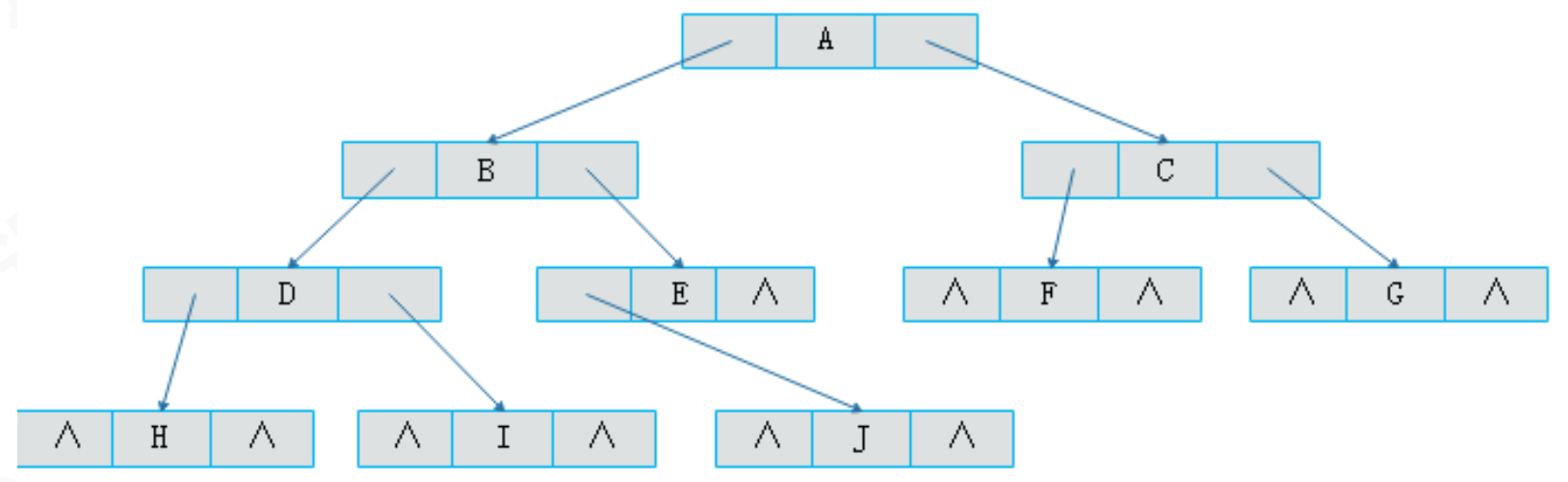
为了避免空间浪费,我们利用这些空指针域完成一些辅助功能,存放在某种遍历次序下该结点的前驱结点和后继结点的指针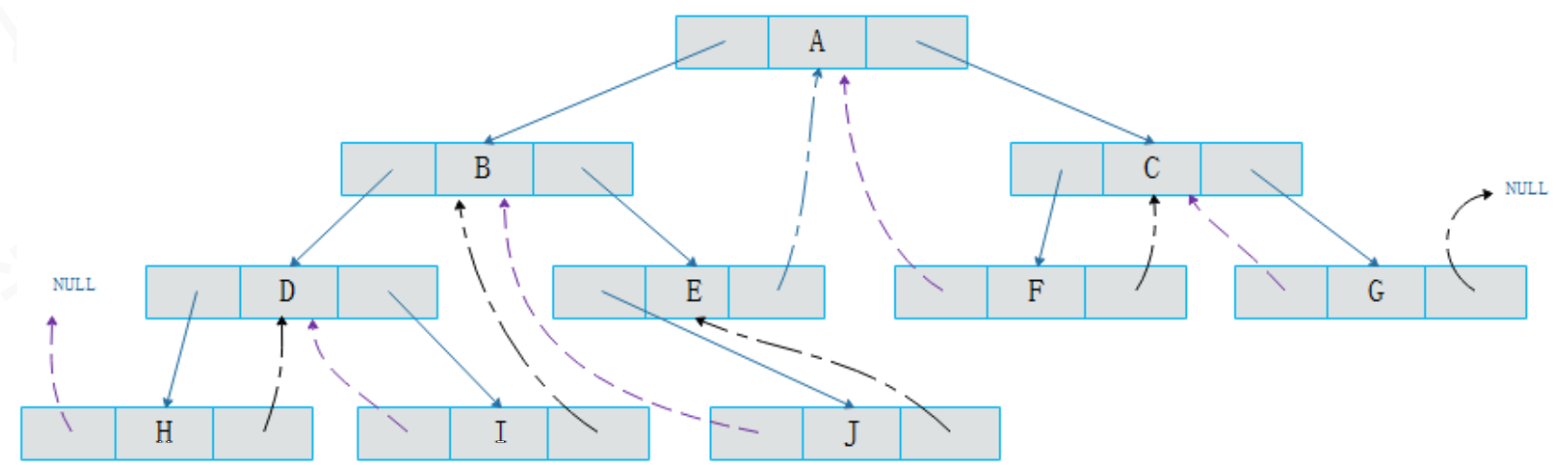
这些指针称之为线索,加上线索的二叉树称之为线索二叉树
1.2 线索化逻辑
线索化的目的:
线索化可以解决空指针域的浪费问题
线索化可以在一个结点寻找它的前驱或后继时更加快捷
线索化的规则:
结点左子树为空,利用左孩子指针指向它的前驱结点
结点右子树为空,利用右孩子指针指向它的后继结点
注意:所有前驱和后继要按照某一种遍历次序
示例:使用中序遍历,记录前驱和后续结点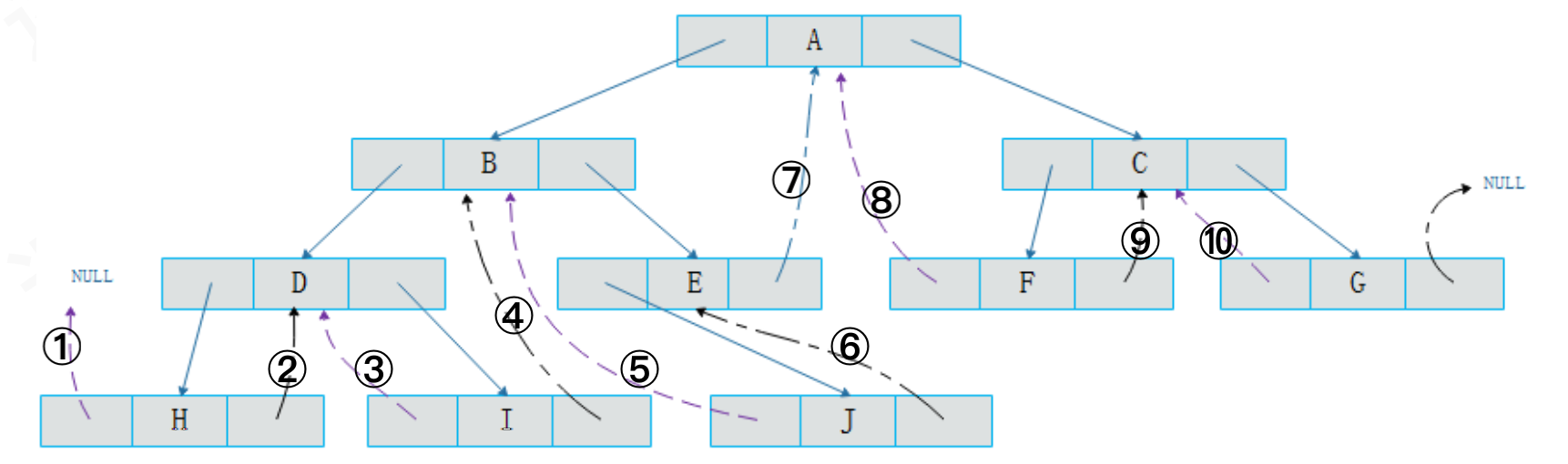
中序遍历结果:
H、D、I、B、J、E、A、F、C、G由于
结点H没有前驱结点,所以左孩子指向空,右孩子指向后继结点D结点I左孩子指向前驱结点D,右孩子指向后继结点B将二叉树线索化,必须经过一轮遍历,通过遍历得到结点之间的前驱和后继关系
线索化的问题:指针域存储的是一个地址,有可能是左右孩子,也可能是前驱后继结点。我们需要将其进行区分,否则遍历后拿到的结果会是混乱的
我们可以在结点的数据结构中增加标记,用于区分存储结点的类型
- 除了
data和两个指针域之外,增加ltag和rtag标记,通过它们区分指针域中存储结点的类型
示例: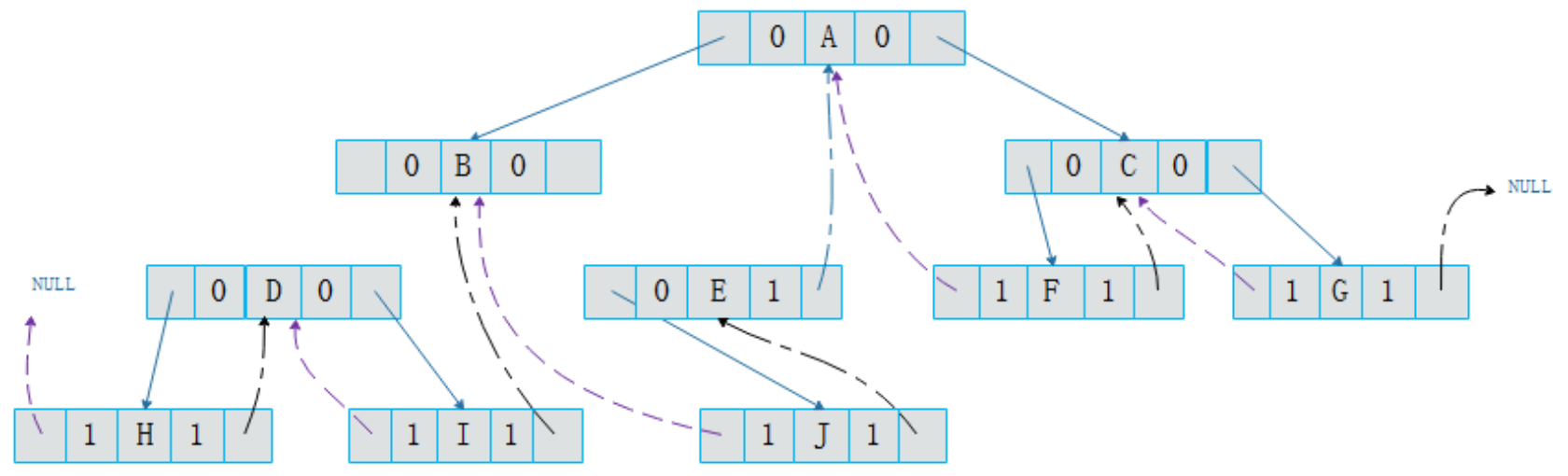
当
ltag为0,表示该指针域指向左孩子。为1,表示指向前驱结点当
rtag为0,表示该指针域指向右孩子。为1,表示指向后继结点
1.3 线索化二叉树创建
1.3.1 二叉树的创建
public struct BiThrTree {enum BiTag : Int {case Link = 0case Thread = 1}fileprivate class BiTNode : Equatable {static func == (lhs: BiThrTree.BiTNode, rhs: BiThrTree.BiTNode) -> Bool {let obj1 = Unmanaged<AnyObject>.passUnretained(lhs).toOpaque();let obj2 = Unmanaged<AnyObject>.passUnretained(rhs).toOpaque();return obj1 == obj2;}var data : Character?;var leftChild : BiTNode?;var rightChild : BiTNode?;var lTag : BiTag?;var rTag : BiTag?;init(){}init(c : Character){self.data = c;}deinit {print(data == nil ? "头结点Node释放" : "值为\(data!)的Node释放");}}fileprivate var _root : BiTNode? = nil;fileprivate mutating func createTree(str : String, index : inout Int, node : inout BiTNode?){if(str.isEmpty){return;}let c = str[index];if(c == "#"){node = nil;return;}node = BiTNode(c: Character(c));if(index == 0){_root = node;}index += 1;if(index >= str.count){return;}createTree(str: str, index: &index, node: &node!.leftChild);if(node!.leftChild != nil){node?.lTag = BiTag.Link;}index += 1;if(index >= str.count){return;}createTree(str: str, index: &index, node: &node!.rightChild);if(node!.rightChild != nil){node?.rTag = BiTag.Link;}}}
1.3.2 线索化的实现
线索化采用中序遍历实现:
public struct BiThrTree {
init(str : String){
var index = 0;
var root : BiTNode?;
createTree(str: str, index: &index, node: &root);
inThreading(node: _root);
}
fileprivate var _pre : BiTNode? = nil;
fileprivate mutating func inThreading(node : BiTNode?){
if(node == nil){
return;
}
inThreading(node: node?.leftChild);
if(node?.leftChild == nil){
node?.leftChild = _pre;
node?.lTag = BiTag.Thread;
}
if(_pre?.rightChild == nil){
_pre?.rightChild = node;
_pre?.rTag = BiTag.Thread;
}
_pre = node;
inThreading(node: _pre?.rightChild);
}
}
inThreading方法解读:
如果某结点的左指针域为空,将
_pre赋值给左指针域,表示它的前驱结点。并修改lTag标记为BiTag.Thread,完成该结点的线索化- 因为其前驱结点刚刚访问过,并且被赋值给
_pre,所以可以将_pre赋值给左指针域
- 因为其前驱结点刚刚访问过,并且被赋值给
如果该结点的前驱结点
_pre没有右孩子,则表示当前node结点就是_pre的后继结点。将node结点赋值给_pre的右指针域,完成_pre结点的线索化当前驱和后继结点的判断结束后,将
node结点赋值给_pre,并进行_pre右孩子的线索化方法调用
1.3.3 线索化的优化
线索化的⼆叉树,在进⾏遍历时,其实就等价于操作⼀个双向链表结构。因为类似双向链表结构,所以我们在⼆叉树线索链表上添加⼀个头结点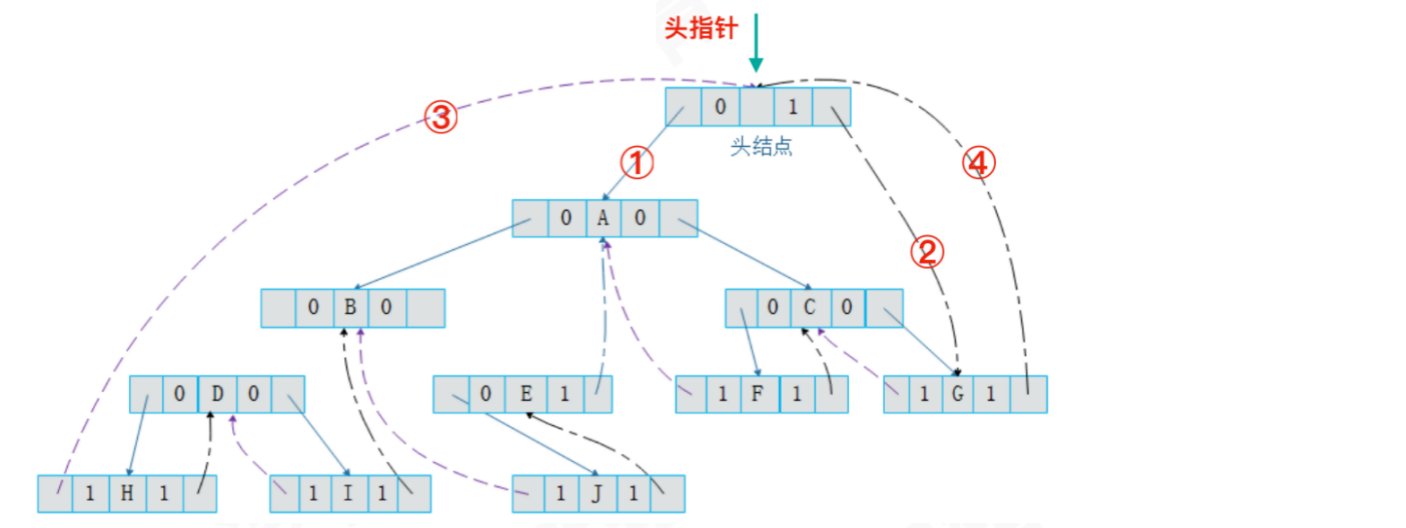
增加头指针
将头结点的左指针域指向二叉树的根结点,并且标记为左孩子
将头结点的右指针域指向中序遍历后的最后一个结点,并且标记为后继结点
将中序遍历后的第一个结点的左指针域,和最后一个结点的右指针域均指向头结点
这样做的好处是,我们可以通过第一个结点,顺着后继结点进行遍历。也可以通过最后一个结点,顺着前驱结点进行遍历
代码实现:
public struct BiThrTree {
fileprivate var _head : BiTNode? = nil;
fileprivate var _root : BiTNode? = nil;
fileprivate var _pre : BiTNode? = nil;
init(str : String){
var index = 0;
var root : BiTNode?;
createTree(str: str, index: &index, node: &root);
_head = BiTNode();
_head?.leftChild = _head;
_head?.lTag = BiTag.Thread;
_head?.rightChild = _head;
_head?.rTag = BiTag.Thread;
inOrderThreading();
}
fileprivate mutating func inOrderThreading(){
_pre = _head;
inThreading(node: _root);
if(_root == nil){
_head?.leftChild = _head;
return;
}
_head?.leftChild = _root;
_head?.lTag = BiTag.Link;
_head?.rightChild = _pre;
_head?.rTag = BiTag.Thread;
_pre?.rightChild = _head;
_pre?.rTag = BiTag.Thread;
}
}
1.4 线索化二叉树遍历
线索化二叉树采用中序遍历的代码实现:
public struct BiThrTree {
func inOrderTraverse() -> String {
var str : String = "";
var node = _head?.leftChild;
while(node != _head){
while(node?.lTag == BiTag.Link){
node = node?.leftChild;
}
str += "\(node!.data!), ";
while(node?.rTag == BiTag.Thread && node?.rightChild != _head){
node = node?.rightChild;
str += "\(node!.data!), ";
}
node = node?.rightChild;
}
return str;
}
}
将
node赋值为根结点,当前node结点不为头结点,视为有效结点,对其进行遍历如果结点的左指针域存储的是左孩子,对其进行遍历,找到第一个结点,并输出它的内容
如果结点的右指针域存储的是线索,并且存储的结点不为头结点,对其进行遍历,并输出它的内容
将
node赋值为右指针域存储的结点,准备下一轮的遍历
2. 哈夫曼树
著名的“霍夫曼编码”的发明⼈戴维·霍夫曼(David Albert Huffman)已于1999年10⽉17⽇因癌症去世,享年74岁。他发明了著名的“霍夫曼编码”
除了霍夫曼编码外,霍夫曼在其他⽅⾯也还有不少创造,⽐如他设计的⼆叉最优搜索树算法就被认为是同类算法中效率最⾼的,因⽽被命名为霍夫曼算法,是动态规划(Dynamic Programming)的⼀个范例
霍夫曼在MIT⼀直⼯作到1967年。之后他转⼊加州⼤学的Santa Cruz分校,是该校计算机科学系的创始⼈,1970 ~ 1973年任系主任,1994年霍夫曼退休
霍夫曼除了获得计算机先驱奖以外,还在1973年获得IEEE的McDowell奖。1998年``IEEE下属的信息论分会为纪念信息论创⽴50周年,授予他Golden Jubilee奖。霍夫曼去世前不久的1999年6⽉,他还荣获以哈明码发明⼈命名的哈明奖章(Hamming Medal)
2.1 哈夫曼编码的背景分析
示例:如果将学生的成绩按不及格、及格、中等、良好、优秀五个等级划分,最简单粗暴的实现方式为:
if(sum < 60)
result = "不及格";
else if(sum < 70)
result = "及格";
else if(sum < 80)
result = "中等";
else if(sum < 90)
result = "良好";
else
result = "优秀";
假设:学生成绩在70 ~ 89分之间占据了70%,但是都需要经过3次判断才能得到正确的结果。那么当数量集⾮常⼤的时候,这样⽐较就会出现效率问题
将上述逻辑以二叉树的形式进行展示: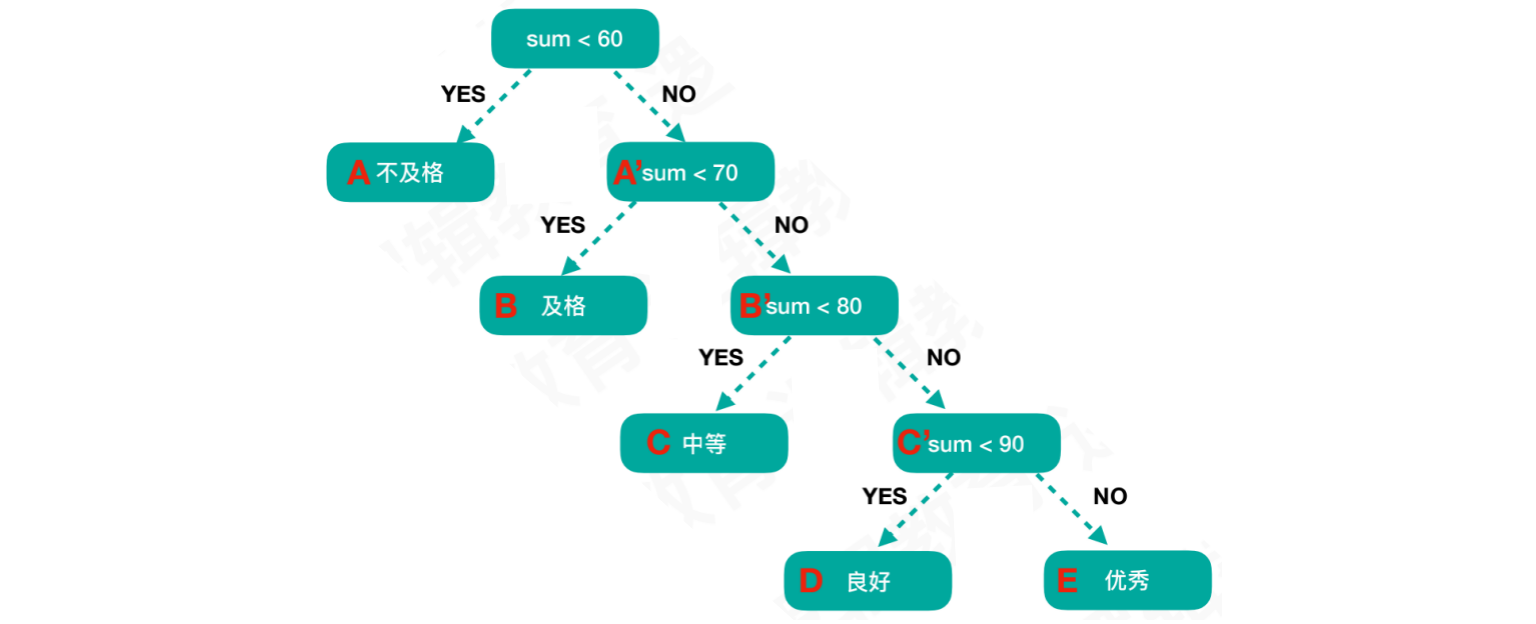
结点D的路程⻓度为4,也就是说当结果为“良好”时,需要经过四次判断树的路径⻓度就指,从树根到每⼀个结点的路径⻓度之和
- 即:A + A’ + B + B’ + C + C’ + D + E = 1 + 1 + 2 + 2 + 3 + 3 + 4 + 4 = 20
我们通过已知信息,也就是成绩的分布规律,可以对二叉树进一步优化: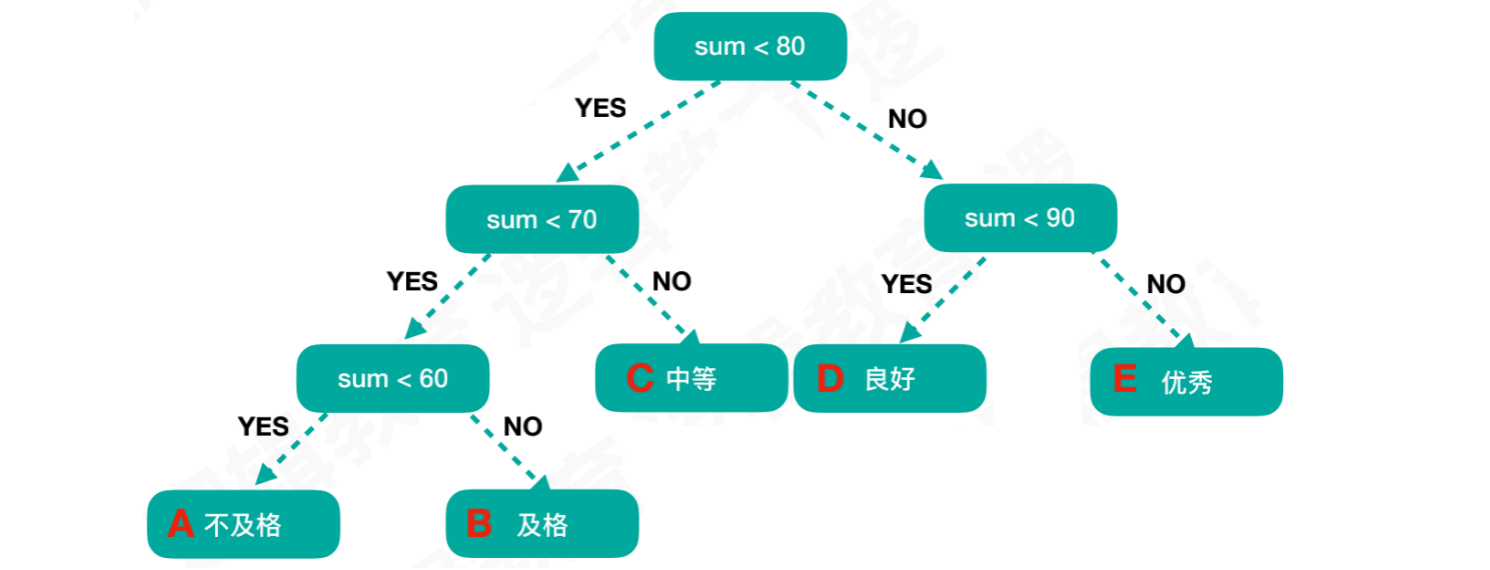
优化后
结点D的路程⻓度为2树的路径⻓度为:B’ + C’ + A’ + C + D + E + A + B = 1 + 1 + 2 + 2 + 2+ 2 + 3 + 3 = 16
假设我们有N个权重值,构建N个叶子结点的二叉树。每个叶子结点等于WK,每个叶子结点都有它的权重值LK
在构建哈夫曼树时,要根据权重值,计算WPL,也就是带权重的路径长度
示例: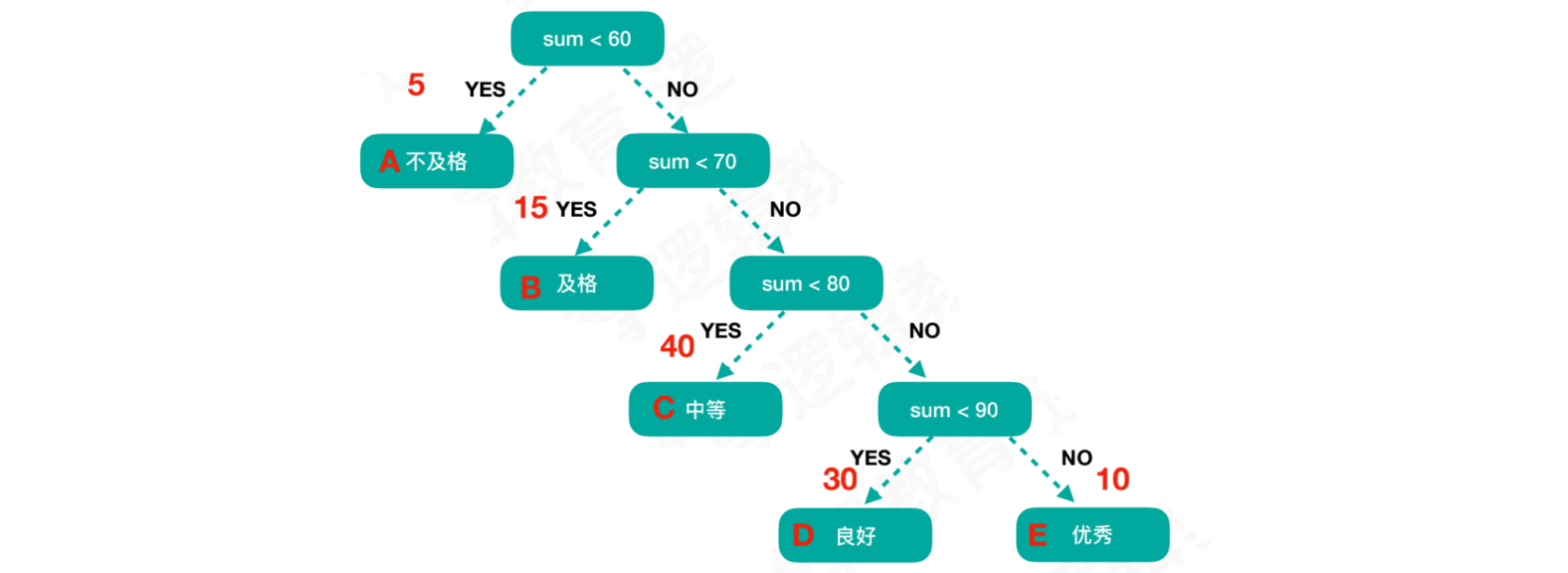
权重值来自于成绩的分布规律,使用结点的路程⻓度乘以权重值进行计算
该二叉树的
WPL= 1 5 + 2 15 + 3 40 + 4 30 + 4 * 10 = 315WPL只会计算二叉树中的叶子结点
优化后的二叉树的WPL: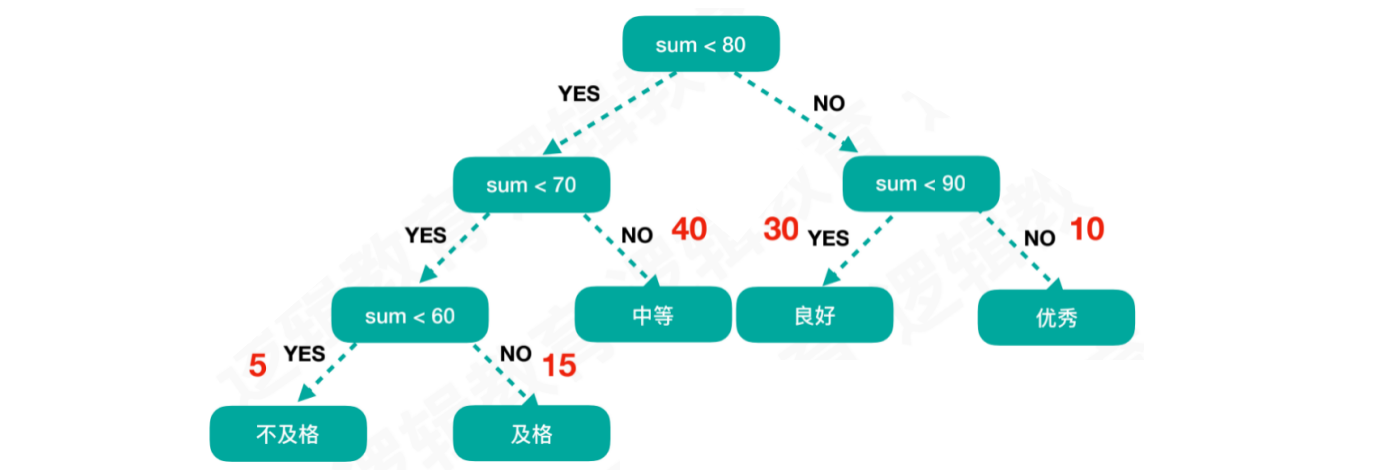
WPL= 3 5 + 3 15 + 2 40 + 2 30 + 2 * 10 = 220
2.2 哈夫曼树的构建逻辑分析
上述示例中,我们只有几个结点的权重值。但我们需要根据权重值构建一颗哈夫曼编码树
2.2.1 构建哈夫曼树
假设:结点A ~ E对应以下几个权重值
结点A = 5,结点B = 15,结点C = 40,结点D = 30,结点E = 10
我们首先对权重值进行排序,找出两个最小权重值,分别为结点A和结点E,将两者之和的权重值构建新结点N1,此时结点N1 = 15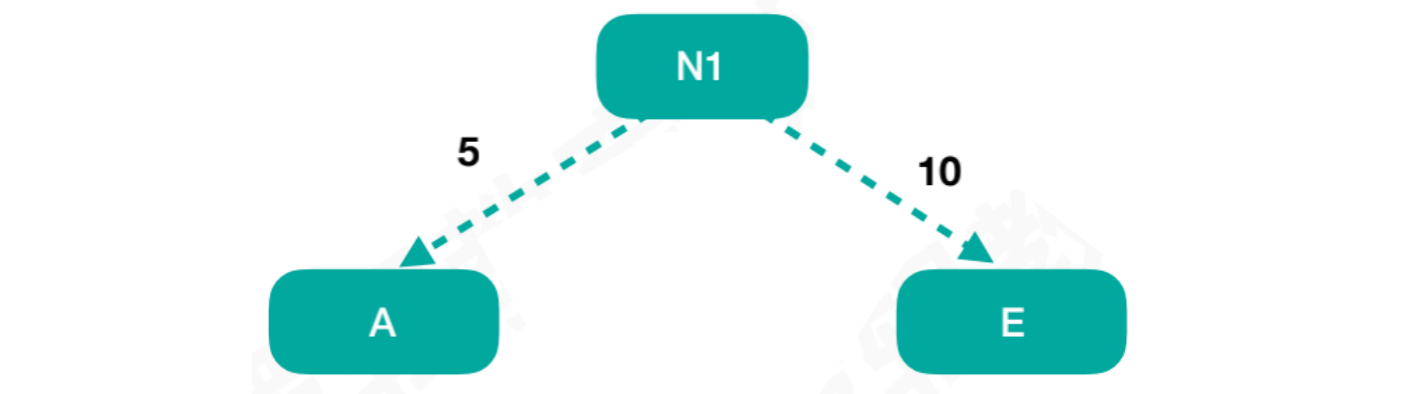
找到剩余结点中的权重值最小的结点B,将结点N1和结点B用同样的方式组合成新结点N2,此时结点N2 = 30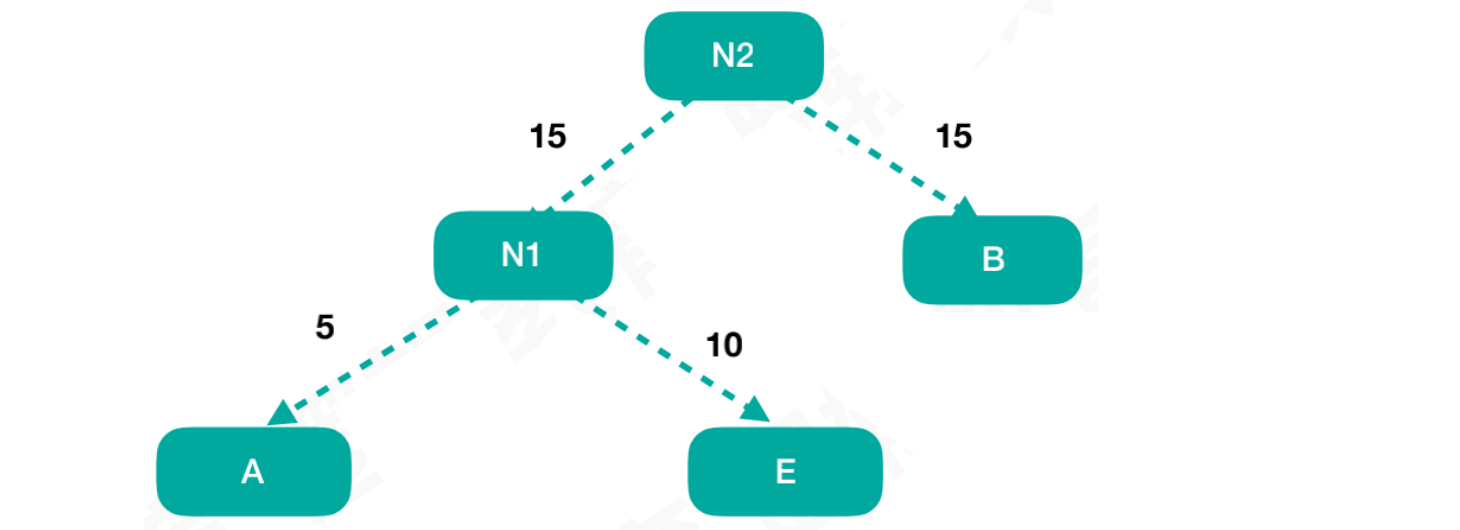
- 构建哈夫曼树的规则,左子树放值小的,右子树放值大的。由于
结点B和结点N1的权重值相等,而结点B为后插入结点,处于右孩子位置
找到剩余结点中的权重值最小的结点C,将结点N2和结点D用同样的方式组合成新结点N3,此时结点N3 = 60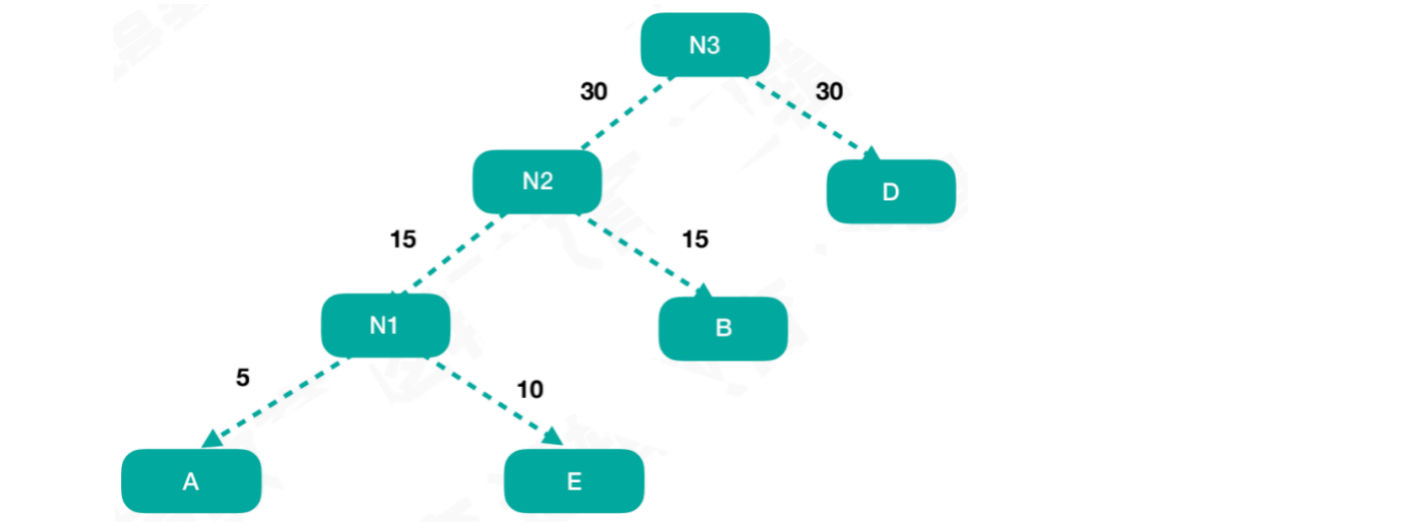
此时只剩下最后一个结点C,将结点N3和结点C用同样的方式组合成新结点T,此时结点T = 100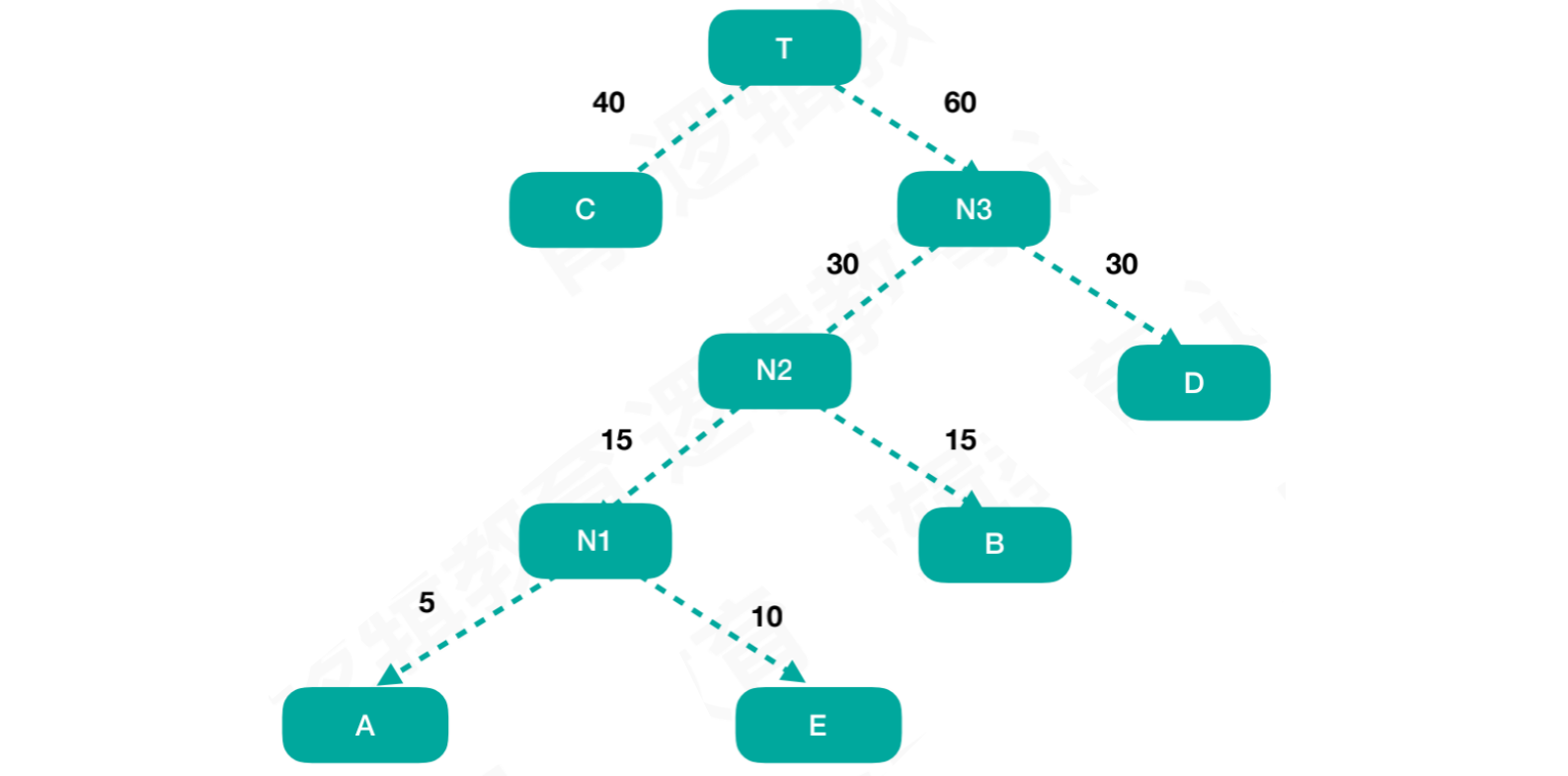
结点T为根结点,由于结点C的权重值小于结点N3,所以结点C为左孩子,结点N3为右孩子此时这颗树的
WPL = 1 * 40 + 2 * 30 + 3 * 15 + 4 * 10 + 4 * 5 = 205
2.2.2 哈夫曼编码的目的
假设:我们要传递的内容为ABCDEF
我们将传递的字符在计算机底层全部为二进制形式,例如:A = 000,B = 001,C = 010,D = 011,E = 100,F = 101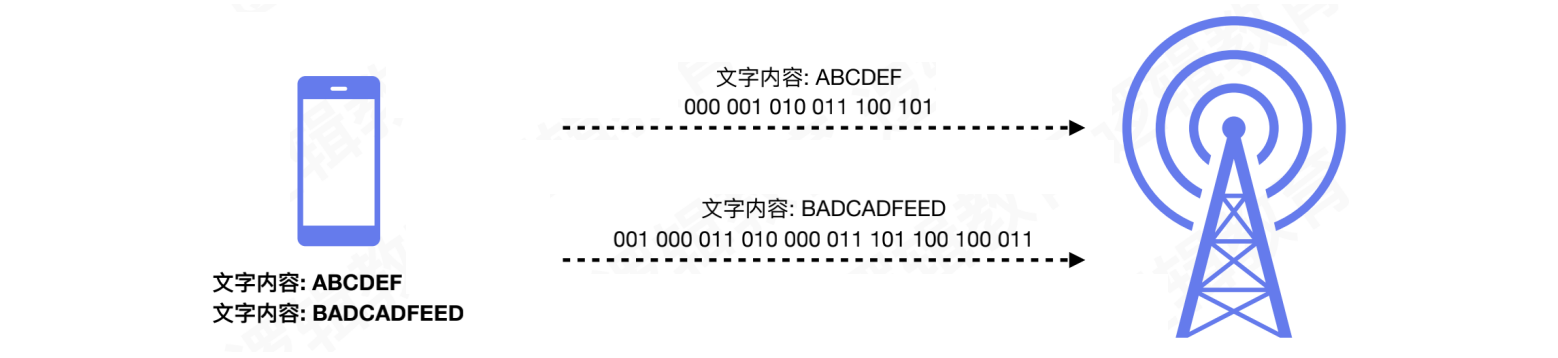
传输之前,我们可以根据权重,对二进制数据进行合理的优化
首先对字符对应权重值,可以通过字符的使用频次定义。然后对权重值进行排序,找出权重值最低的两个字符F和B
将F和B的权重值相加,组合新结点N1,结点N1 = 13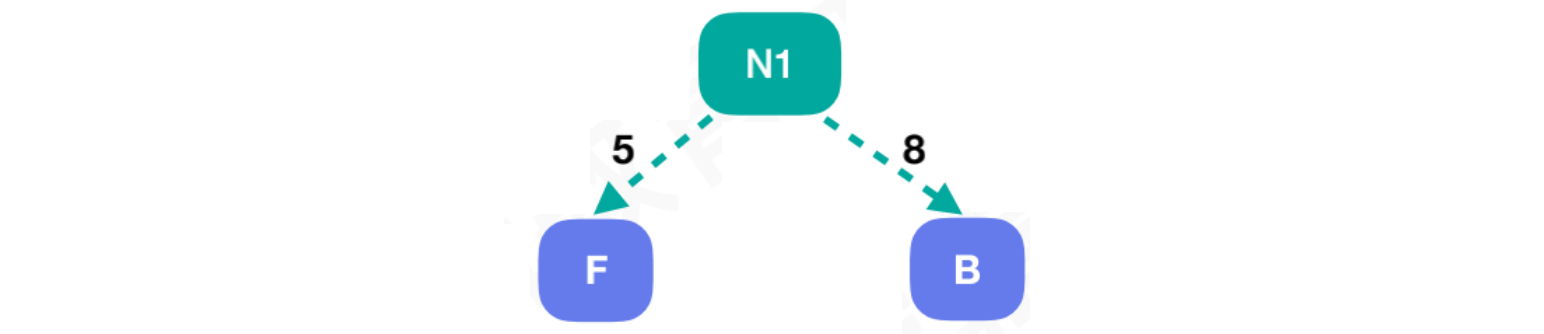
将剩余结点排序,找到权重值最小的结点C。将结点N1和结点C的权重值相加,组合新结点N2,结点N2 = 28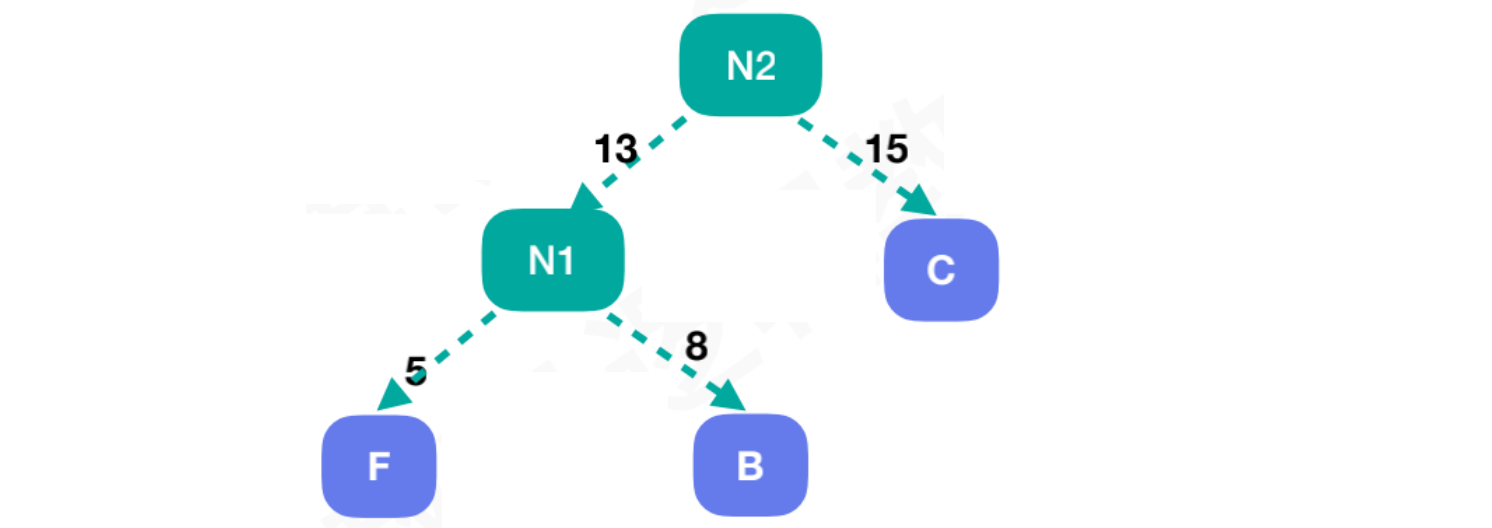
在剩余结点中,结点D和结点A的权重值都小于结点N2,所以将结点D和结点A组合一颗新的树,它们的权重值相加,组合新结点N3,此时结点N3 = 42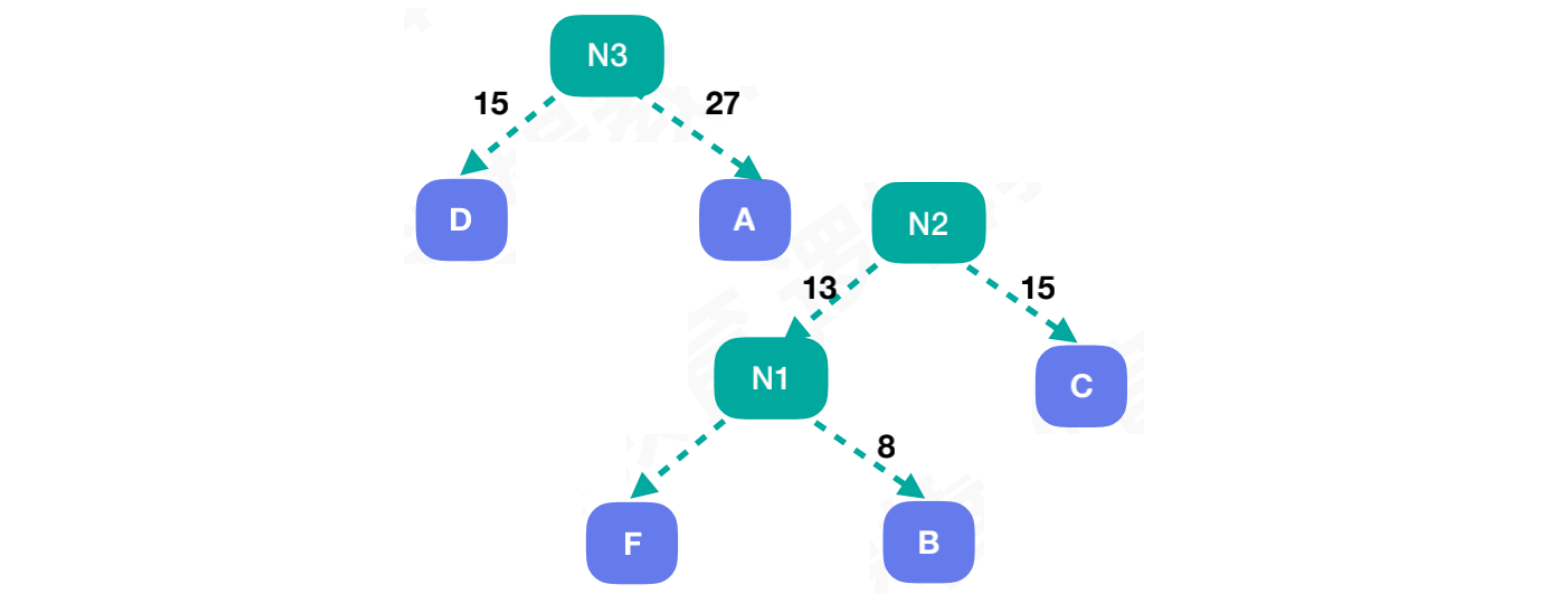
将结点N2和最后一个结点E,组合新结点N4,此时结点N4 = 58。现在我们拥有N3和N4两颗独立的子树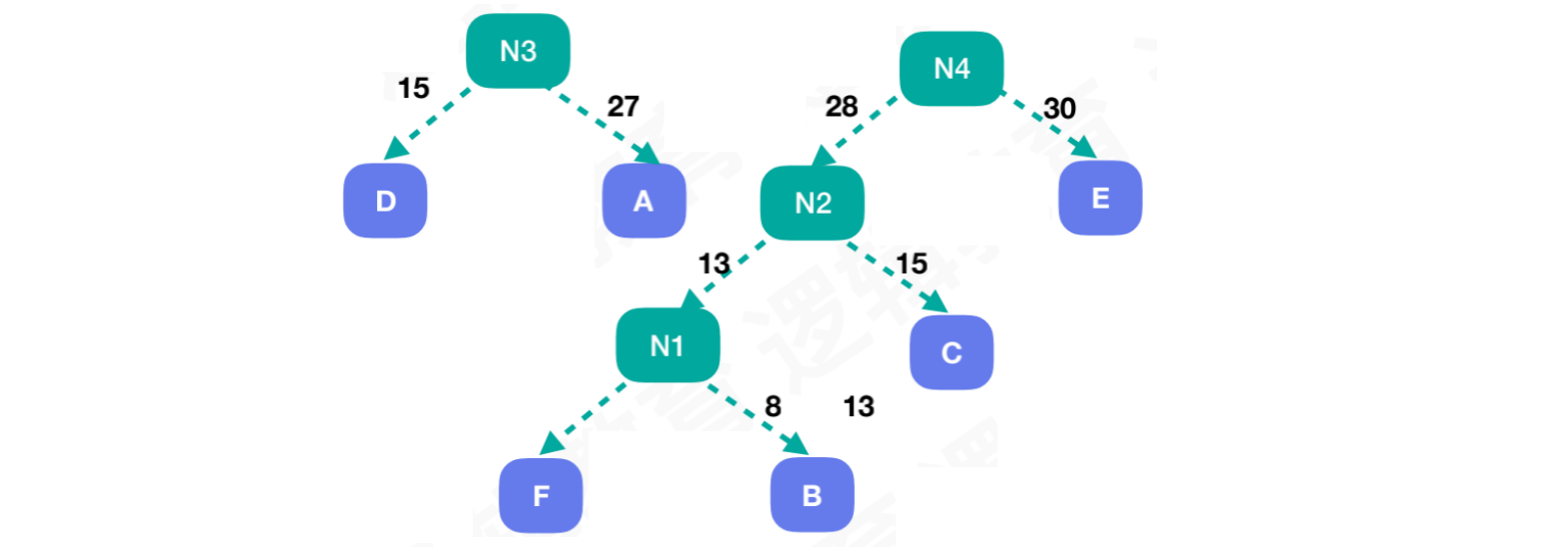
最后将N3和N4两颗子树,合并成一颗哈夫曼树。将结点N3和结点N4组合新结点T,此时结点T = 100。结点T为根结点,权重值小的N3为左孩子,权重值大的N4位右孩子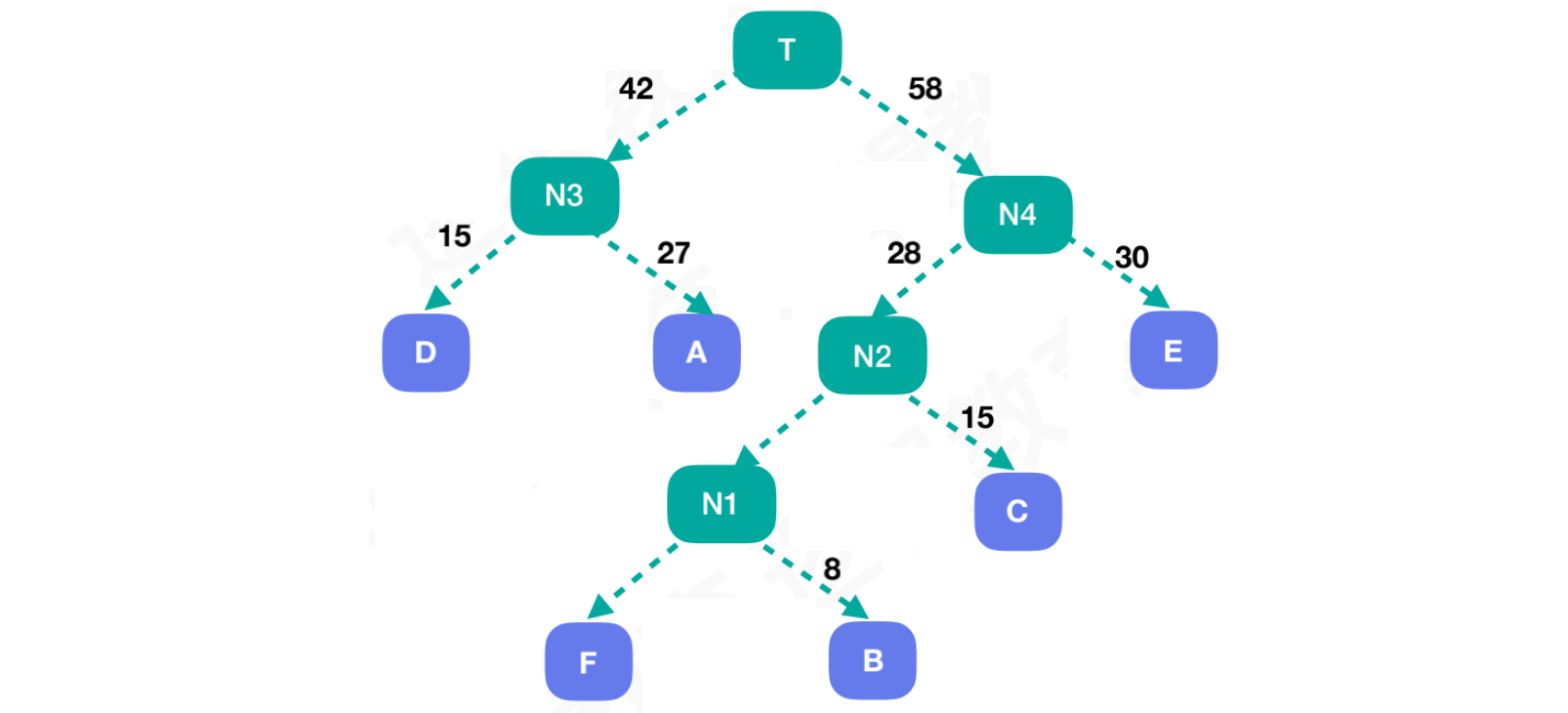
- 构建哈夫曼树之前,我们只有权重值。以左孩子存储权重值小的结点,右孩子存储权重值大的结点为规则。构建出哈夫曼树,保证其结点权重值尽可能平衡
得到哈夫曼树之后,开始我们对数据的进一步优化。我们将哈夫曼树中所有左子树的权重值设置为0,右子树的权重值设置为1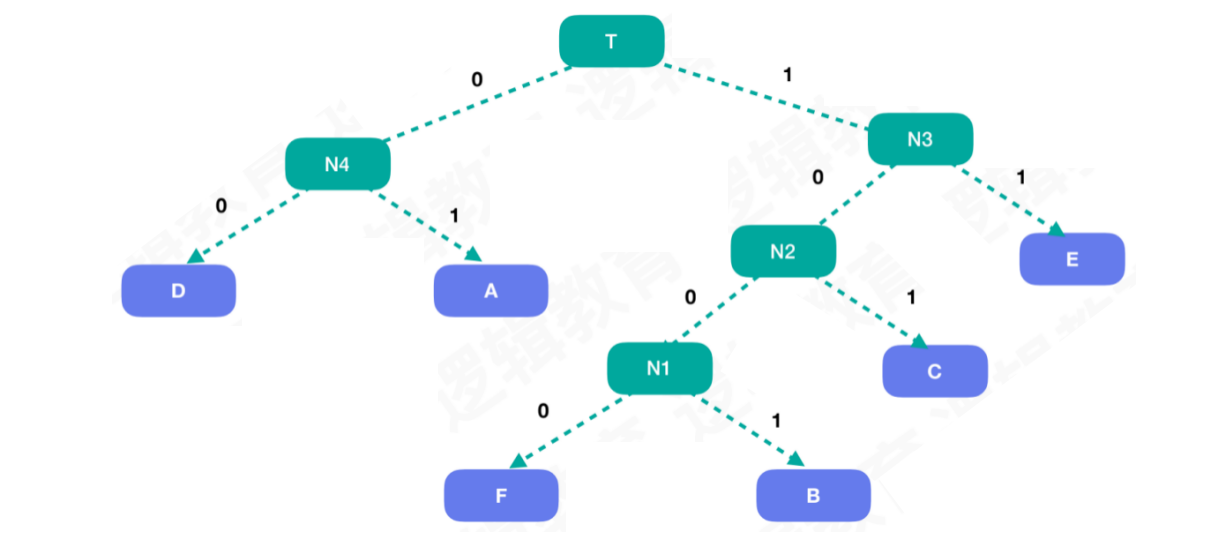
根据修改后的权重值,重新调整字符对应的二进制数据。A = 01,B = 1001,C = 101,D = 00,E = 11,F = 1000
其中A和E的二进制长度最短,因为它们的出现频次最高。而B和F最长,因为它们的出现频次最低
哈夫曼编码的目的,根据字符串中每个字符的权重值,重新调整它们的编码长度,而不是所有字符的长度一概而论
以传输字符串BADCADFEED为例:
原编码的⼆进制:001 000 011 010 000 011 101 100 100 011,共计30个字符
新编码的⼆进制:1001 01 00 101 01 00 1000 11 11 00,共计25个字符
2.3 哈夫曼树的实现
设计一个哈夫曼树的结点形式:
weight:权重值parent:双亲结点下标leftChild:左孩子下标rightChild:右孩子下标flag:标记,0表示该结点未合并到哈夫曼树中,1表示该结点已经合并到哈夫曼树中
权重值为我们的已知条件,我们要根据权重值来产生新的结点,以此类推,最终构建出完整的哈夫曼树
定义哈夫曼树的结点结构:
class HaffTree {
fileprivate class HaffNode {
var weight : Int;
var parent : Int;
var leftChild : Int;
var rightChild : Int;
var flag : Int;
init(){
self.weight = 0;
self.parent = 0;
self.leftChild = -1;
self.rightChild = -1;
self.flag = 0;
}
}
}
创建哈夫曼树的代码实现:
class HaffTree {
fileprivate var _n : Int = 0;
fileprivate var _arr : [HaffNode]? = nil;
func create(source : [Int]){
_n = source.count;
_arr = [HaffNode].init();
for i in 0 ..< 2 * _n - 1 {
let node = HaffNode();
if(i < _n){
node.weight = source[i];
}
_arr?.append(node);
}
for i in 0 ..< _n - 1 {
var m1 = Int.max;
var m2 = Int.max;
var x1 = 0;
var x2 = 0;
for j in 0 ..< _n + i {
let node = _arr![j];
if(node.weight < m1 && node.flag == 0){
m2 = m1;
x2 = x1;
m1 = node.weight;
x1 = j;
continue;
}
if(node.weight < m2 && node.flag == 0){
m2 = node.weight;
x2 = j;
continue;
}
}
let k = _n + i;
let node1 = _arr![x1];
node1.parent = k;
node1.flag = 1;
let node2 = _arr![x2];
node2.parent = k;
node2.flag = 1;
let node3 = _arr![k];
node3.weight = node1.weight + node2.weight;
node3.leftChild = x1;
node3.rightChild = x2;
}
}
}
create方法传入的source参数为已知条件,一个权重值的集合source中的数据为叶子结点,当二叉树中存在n个叶子结点,会对应生成2n - 1个非叶子结点初始化
_arr,循环2n - 1次,初始化所有结点,并设置叶子结点的权重值循环
n - 1次非叶子结点,将m1和m2初始化为一个很大的数字,将x1和x2默认设置为0循环
n + i次,找到未合并到哈夫曼树中的两个最小权重值的结点m1和m2记录两个最小权重x1和x2记录两个最小权重在_arr中的索引值
找到两颗权重值最小的子树,将它们的双亲结点索引值设置为
n + i,并将这两个结点标记为已经合并到哈夫曼树中找到
n + i索引中的结点,设置它的权重值为两颗子树的权重之和,并将它的左孩子和右孩子的索引值设置为x1和x2
2.4 哈夫曼编码的实现
哈夫曼编码的结点形式:
bit:数组,存储编码后的值,例如:编码后的101,存储在数组中[1, 0, 1]start:编码长度weight:字符的权重值
通过哈夫曼树,获取每一个权重值所对应的哈夫曼编码
定义哈夫曼编码的结点结构:
class HaffTree {
class HaffCode {
var bit : [String];
var start : Int;
var weight : Int;
init(){
self.bit = [String]();
self.start = 0;
self.weight = 0;
}
}
}
获取哈夫曼编码的代码实现:
class HaffTree {
func getHaffCode() -> [HaffCode]? {
if(_n == 0){
return nil;
}
var arrCode = [HaffCode]();
for i in 0 ..< _n {
let code = HaffCode();
code.weight = _arr![i].weight;
var child = i;
var parent = _arr![child].parent;
while(parent > 0){
if(_arr![parent].leftChild == child){
code.bit.append("0");
}
else {
code.bit.append("1");
}
child = parent;
parent = _arr![child].parent;
code.start += 1;
}
code.bit = code.bit.reversed();
arrCode.append(code);
}
return arrCode;
}
}
n个权重值,对应n个编码。创建数组arrCode存储编码对象循环
n次,创建HaffCode对象,对weight进行赋值。将当前索引值i赋值给child,通过child得到当前结点,得到当前结点的双亲结点索引值遍历双亲结点,如果当前结点为双亲结点的左孩子,
bit数组中追加0。否则为右孩子,追加1继续向上找双亲结点,同时将编码长度
+1当
parent为0时,证明找到根结点,停止遍历。将bit数组进行倒叙,将编码对象加入到数组中
测试哈夫曼编码:
let source = [2, 4, 5, 7];
let haffTree = HaffTree();
haffTree.create(source: source);
let arrCode = haffTree.getHaffCode();
if(arrCode != nil){
var wpl = 0;
for code in arrCode! {
print("权重值:\(code.weight),编码:\(code.bit.joined())");
wpl += code.start * code.weight;
}
print("WPL:\(wpl)");
}
-------------------------
//输出以下内容:
权重值:2,编码:110
权重值:4,编码:111
权重值:5,编码:10
权重值:7,编码:0
WPL:35
总结
线索化二叉树:
产生背景
一个结点为
N的二叉树,存在N - 1条有效路径,同时也存在N + 1个空指针域为了避免空间浪费,我们利用这些空指针域完成一些辅助功能,存放在某种遍历次序下该结点的前驱结点和后继结点的指针
这些指针称之为线索,加上线索的二叉树称之为线索二叉树
线索化的目的
线索化可以解决空指针域的浪费问题
线索化可以在一个结点寻找它的前驱或后继时更加快捷
线索化的规则
结点左子树为空,利用左孩子指针指向它的前驱结点
结点右子树为空,利用右孩子指针指向它的后继结点
注意:所有前驱和后继要按照某一种遍历次序
线索化的问题
指针域存储的是一个地址,有可能是左右孩子,也可能是前驱后继结点。我们需要将其进行区分,否则遍历后拿到的结果会是混乱的
解决办法:可以在结点的数据结构中增加标记,用于区分存储结点的类型
当
ltag为0,表示该指针域指向左孩子。为1,表示指向前驱结点当
rtag为0,表示该指针域指向右孩子。为1,表示指向后继结点
线索化的优化
线索化的⼆叉树,在进⾏遍历时,其实就等价于操作⼀个双向链表结构。因为类似双向链表结构,所以我们在⼆叉树线索链表上添加⼀个头结点
- 增加头指针
- 将头结点的左指针域指向二叉树的根结点,并且标记为左孩子
- 将头结点的右指针域指向中序遍历后的最后一个结点,并且标记为后继结点
- 将中序遍历后的第一个结点的左指针域,和最后一个结点的右指针域均指向头结点
- 这样做的好处是,我们可以通过第一个结点,顺着后继结点进行遍历。也可以通过最后一个结点,顺着前驱结点进行遍历
哈夫曼树:
背景分析
给定
N个权值作为N个叶子结点,构造一颗二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树。哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近带权路径长度
WPL,使用结点的路程⻓度乘以权重值进行计算WPL只会计算二叉树中的叶子结点
逻辑分析
对权重值进行排序,找出两个最小权重值,将两者之和的权重值构建新结点
权重值小的结点为新结点的左孩子
权重值大的结点为新结点的右孩子
从剩余结点和新结点中继续找最小权重值,构建新结点
循环往复,构建到根结点为止
以左孩子存储权重值小的结点,右孩子存储权重值大的结点为规则。构建出哈夫曼树,保证其结点权重值尽可能平衡
哈夫曼编码的目的
- 根据字符串中每个字符的权重值,重新调整它们的编码长度,而不是所有字符的长度一概而论

