1. 概述
1.1 连通图的⽣成树
连通图的⽣成树定义:
所谓⼀个连通图的⽣成树,它不是树,而是⼀个极⼩的连通⼦图。它含有图中全部的N个顶点,但只⾜以构成⼀颗树的N - 1条边
定义解读:满⾜以下三个条件则为连通图的⽣成树
图是连通图
图中包含
N个顶点图中边的数量等于
N - 1条边
示例:连通图的⽣成树的判断: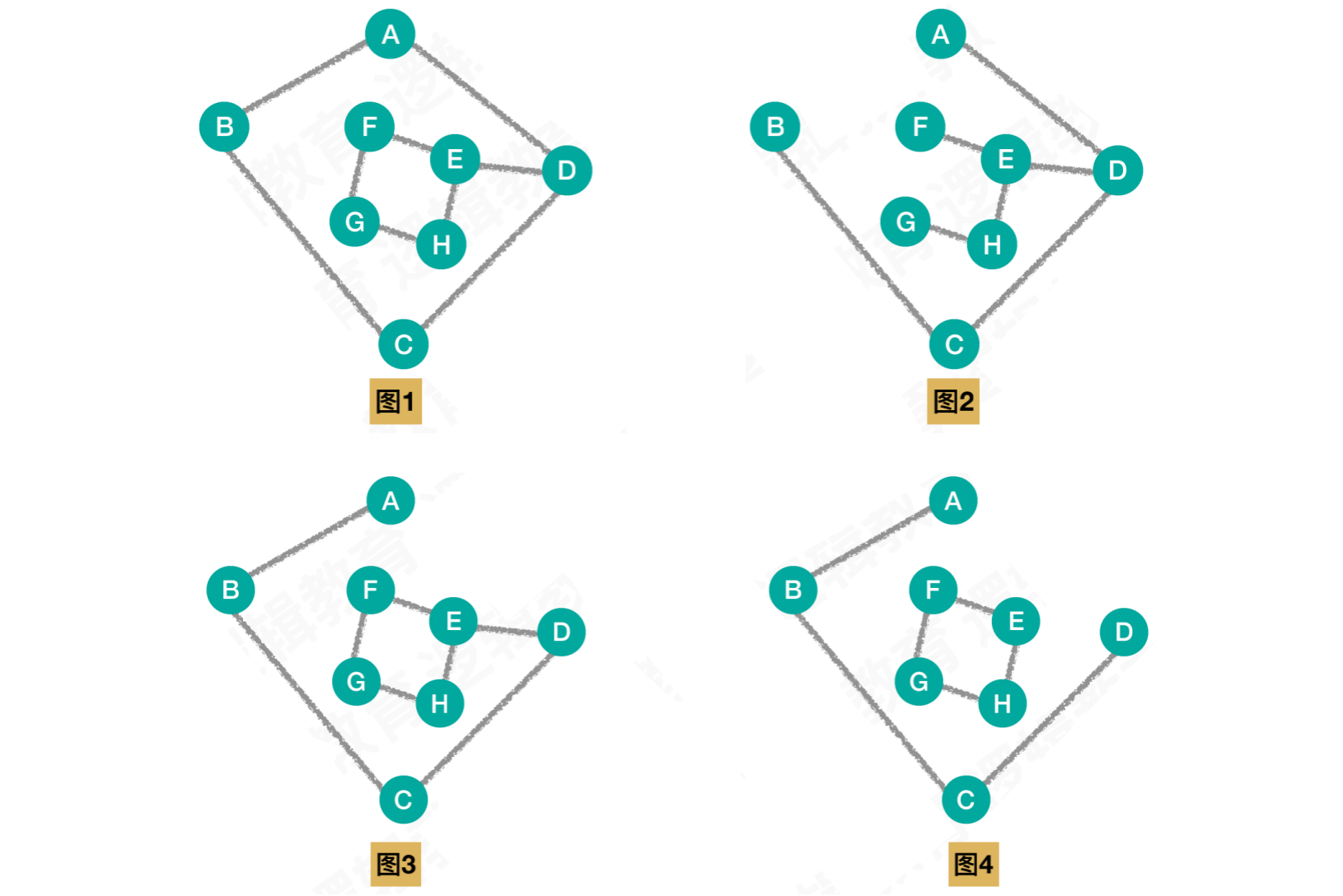
图1:图中边的数量超过
N - 1条边,不是连通图的⽣成树图2:满足三个条件,是连通图的⽣成树
图3:图中边的数量超过
N - 1条边,不是连通图的⽣成树图4:不是连通图,不是连通图的⽣成树
1.2 最小生成树
最⼩⽣成树:把构成连通⽹的最⼩代价的⽣成树称为最⼩⽣成树
例如:设计⼀个最⼩成本的⽹络布线路线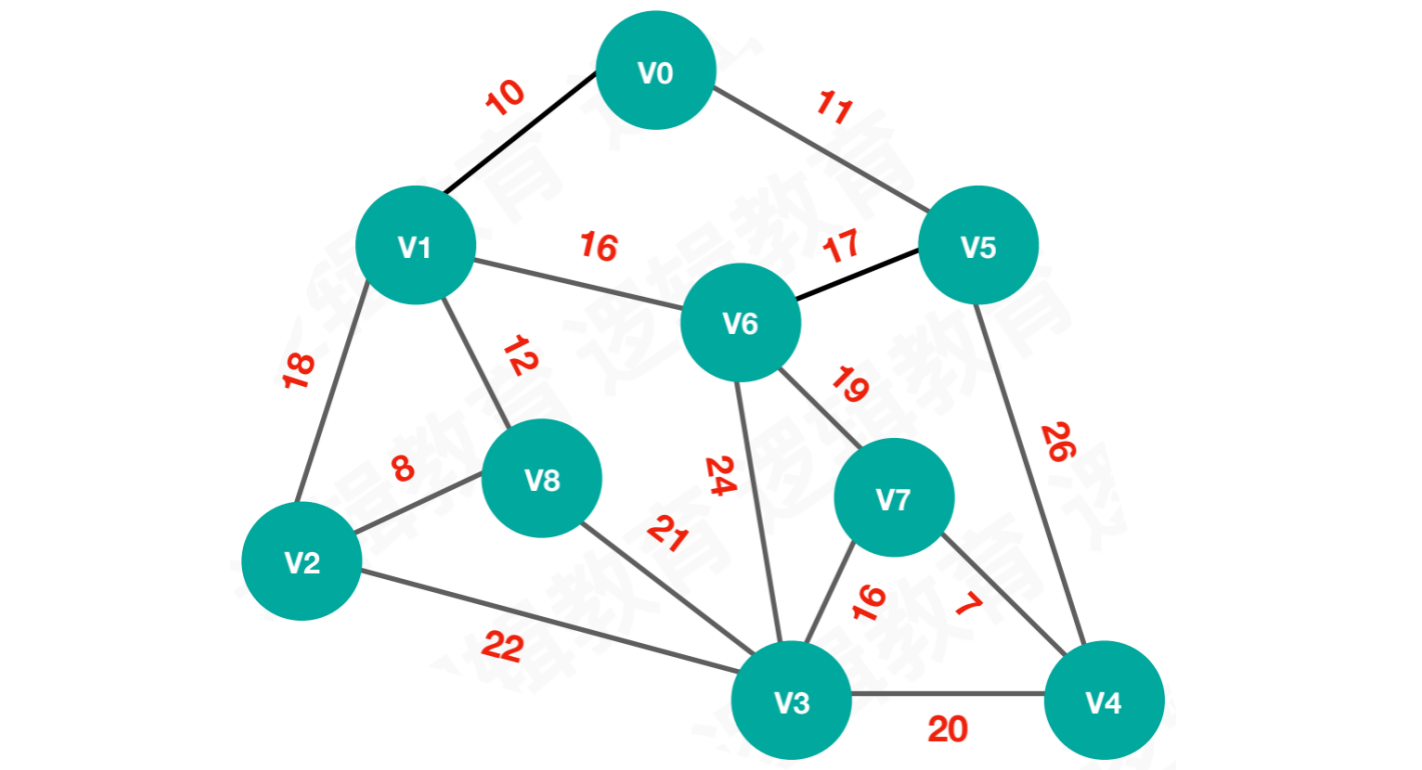
【方案1】:11 + 26 + 20 + 22 + 18 + 21 + 24 + 19 = 161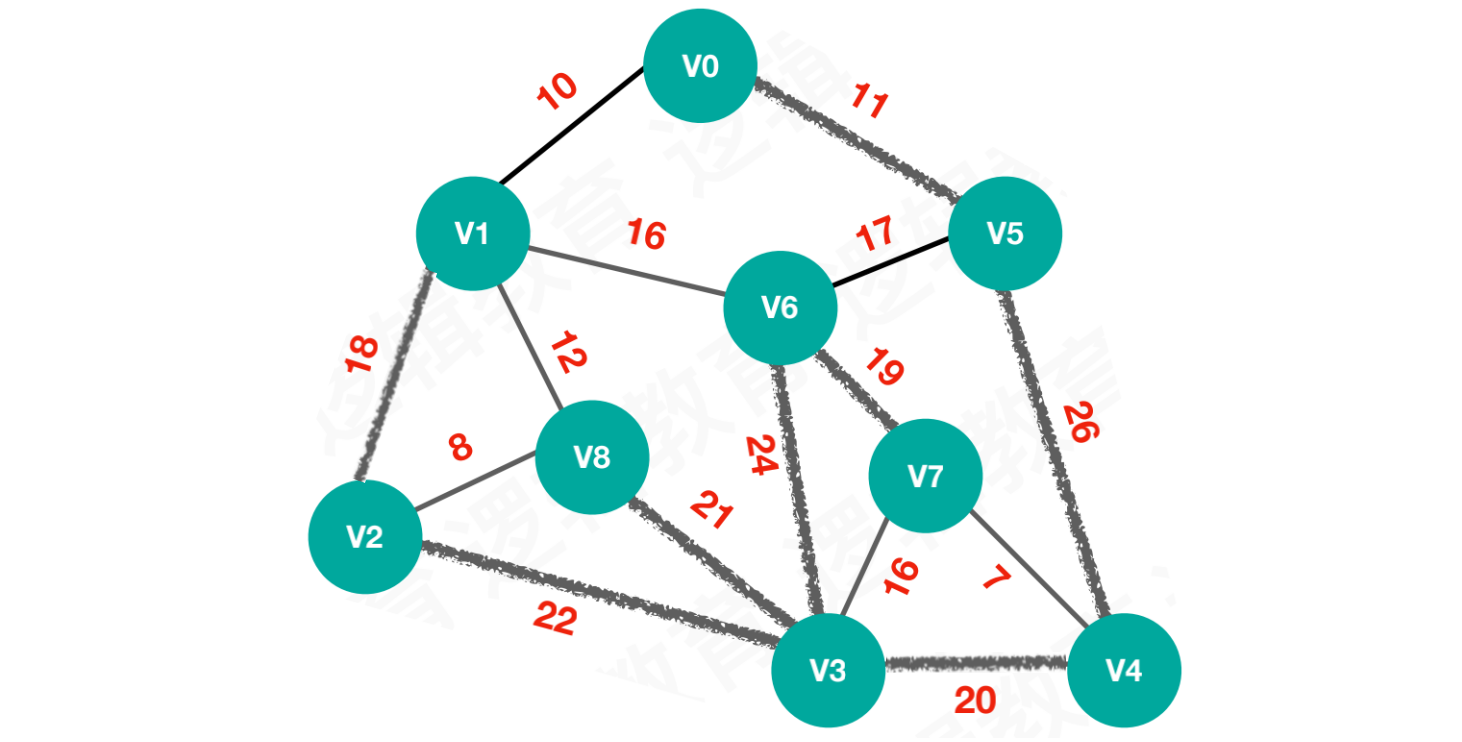
【方案2】:8 + 12 + 10 + 11 + 17 + 19 + 16 + 7 = 100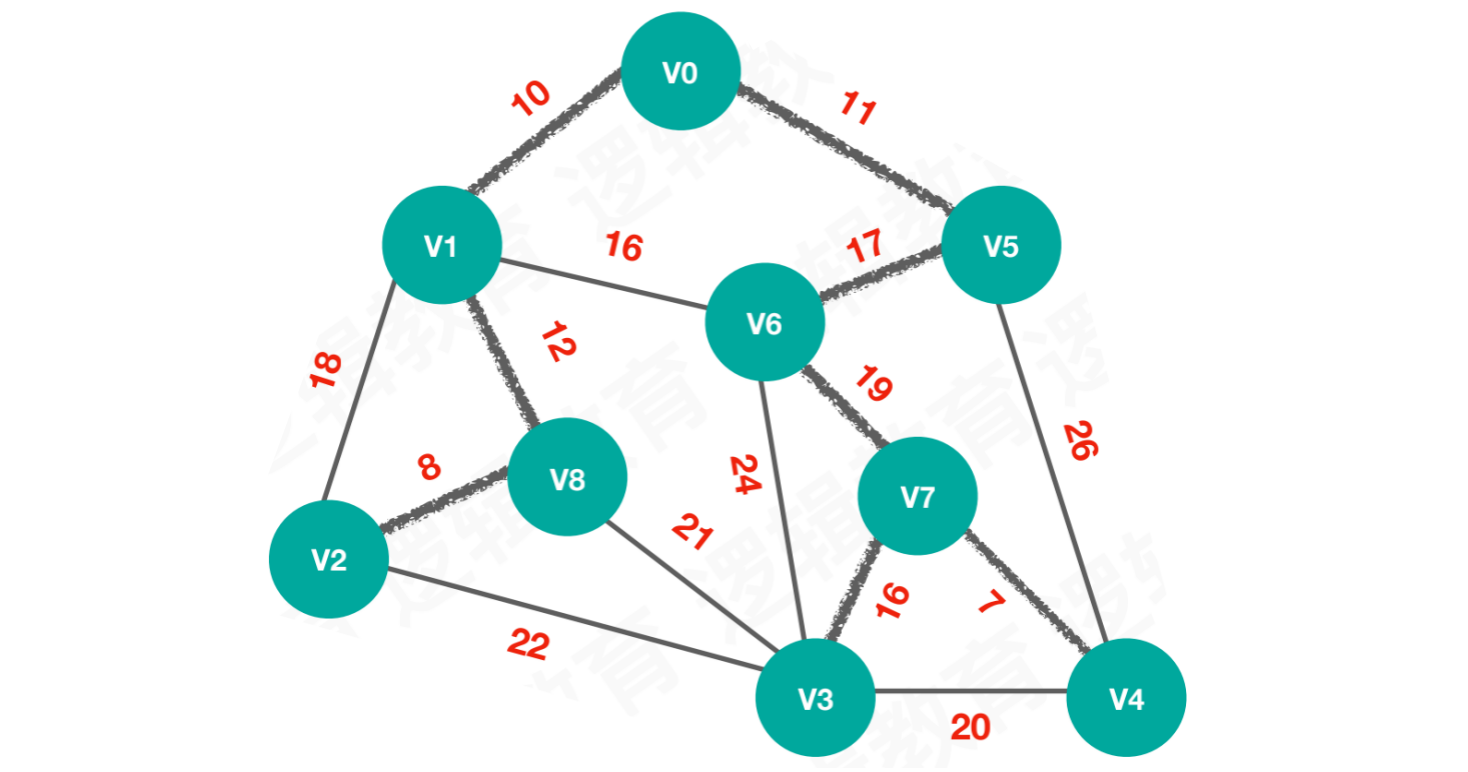
【方案3】:8 + 12 + 10 + 11 + 16 + 19 + 16 + 7 = 99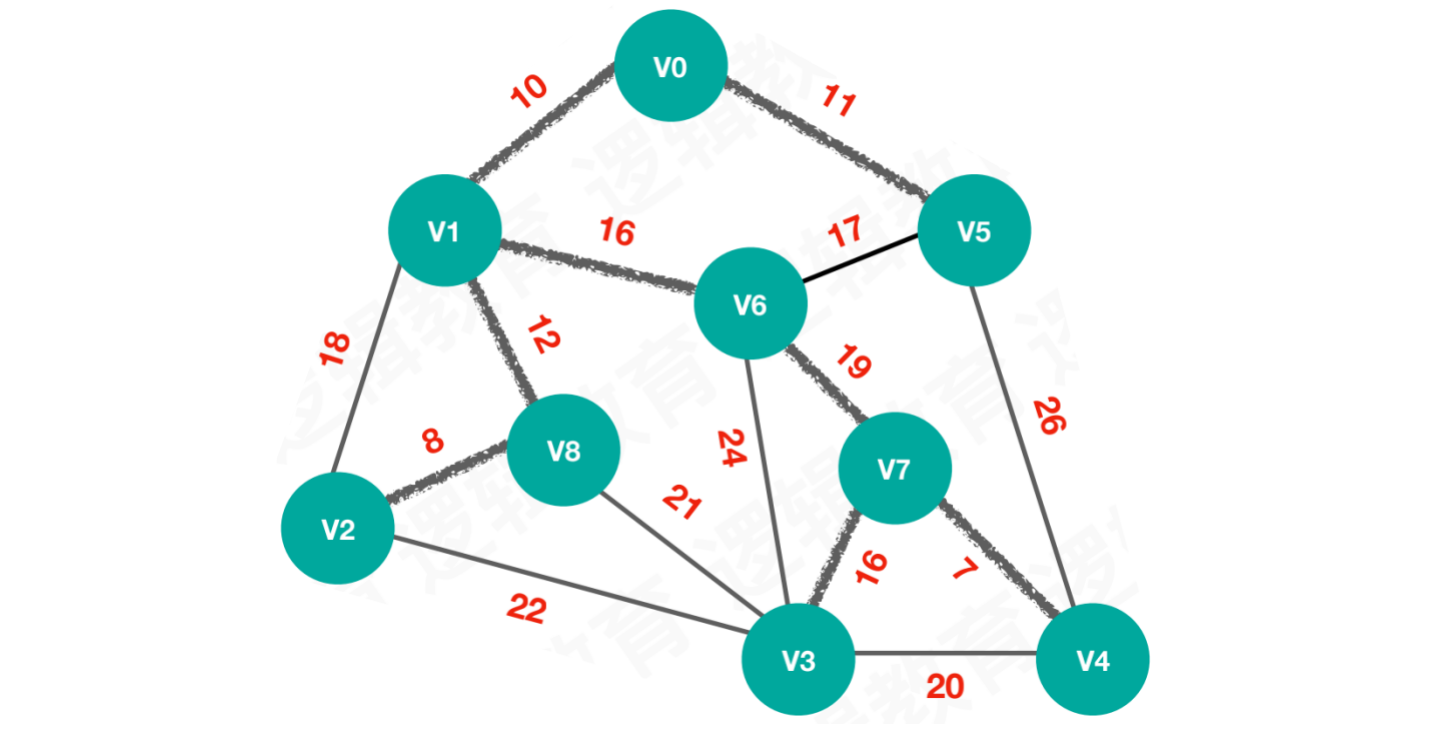
此时,我们需要一个算法,能够精准计算出⽹图的最佳⽅案
2. 普⾥姆(Prim)算法
Prim算法特点:从任意一个顶点开始,每次选择一个与当前顶点集最近的一个顶点,并将两顶点之间的边加入到树中。Prim算法在找当前最近顶点时使用到了贪心算法
贪心算法:在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,算法得到的是在某种意义上的局部最优解
【步骤一】从顶点v0出发,待选择的路线为10和11,优先选择权值更小的路线10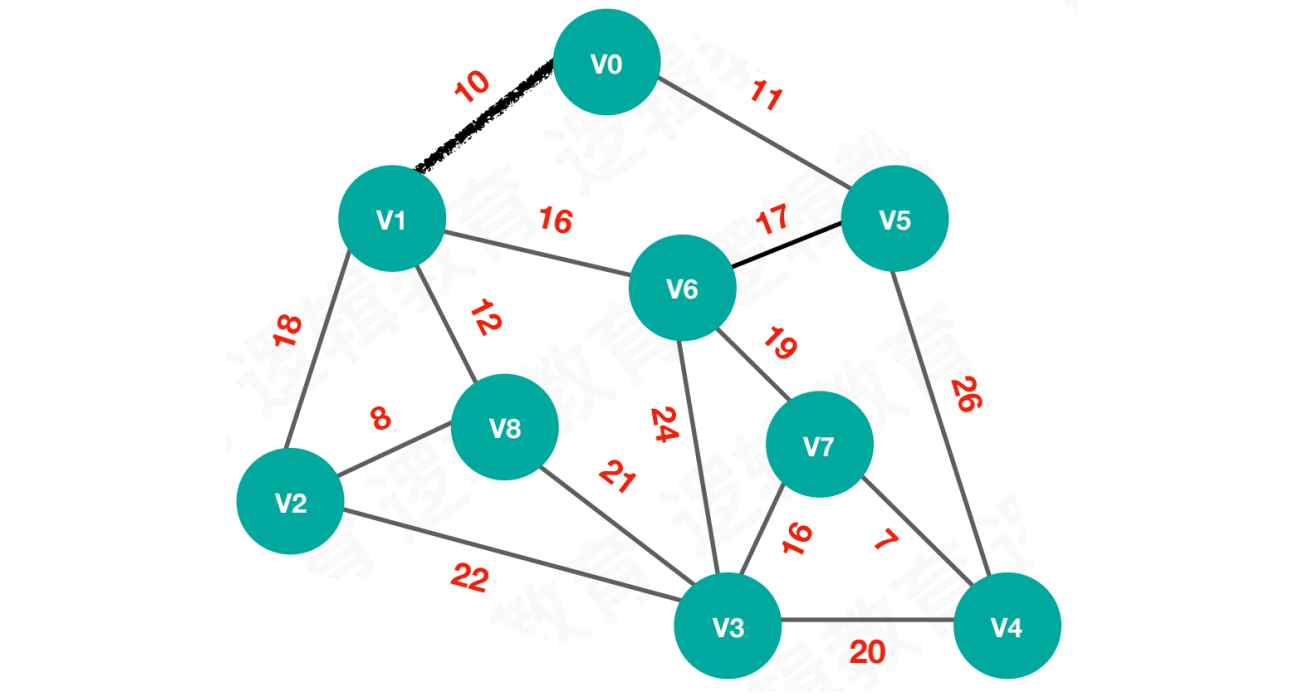
【步骤二】待选择的路线为11、18、12、16,选择路线11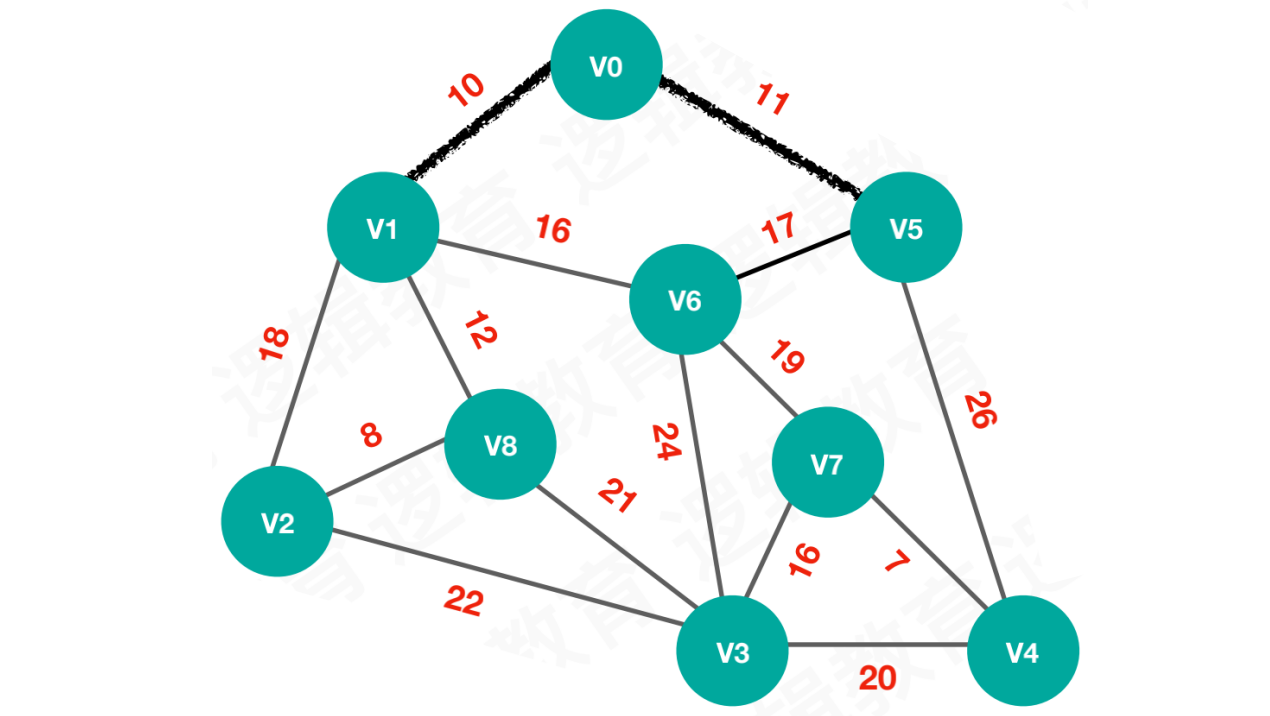
【步骤三】待选择的路线为17、26、18、12、16,选择路线12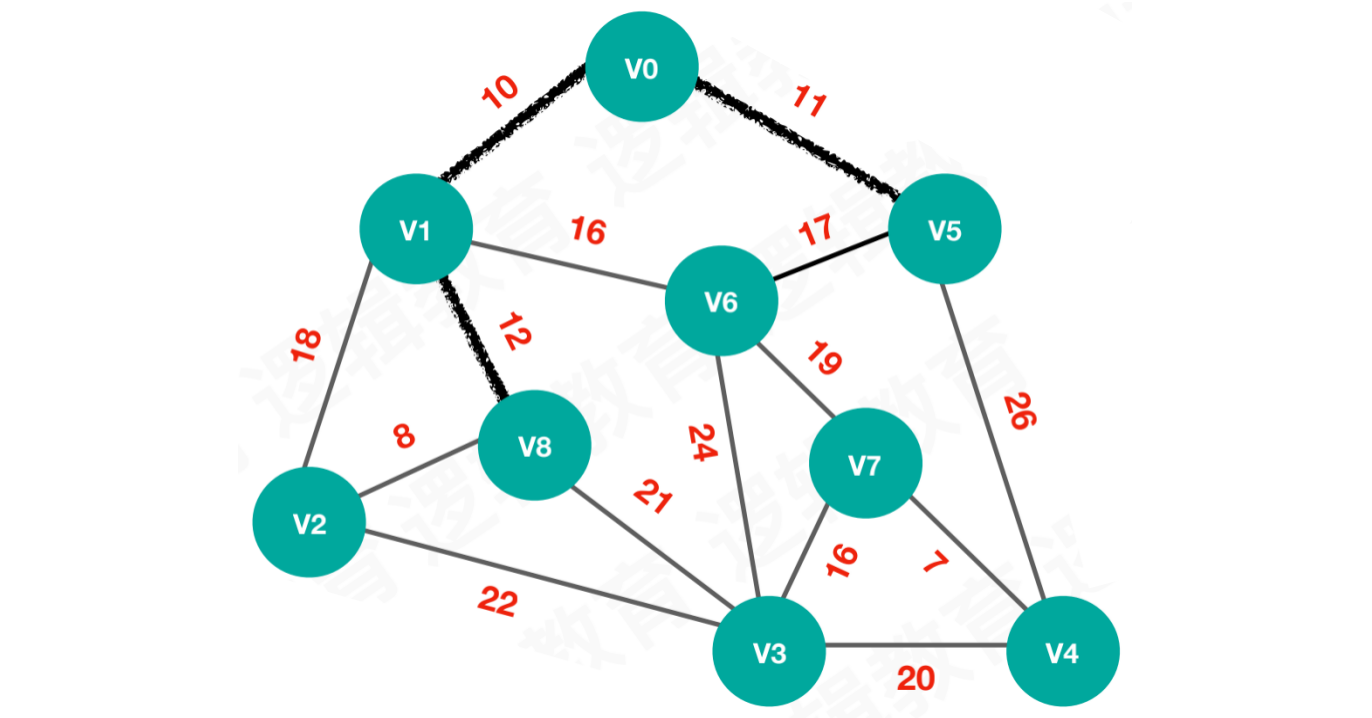
【步骤四】待选择的路线为17、26、18、16、8、21,选择路线8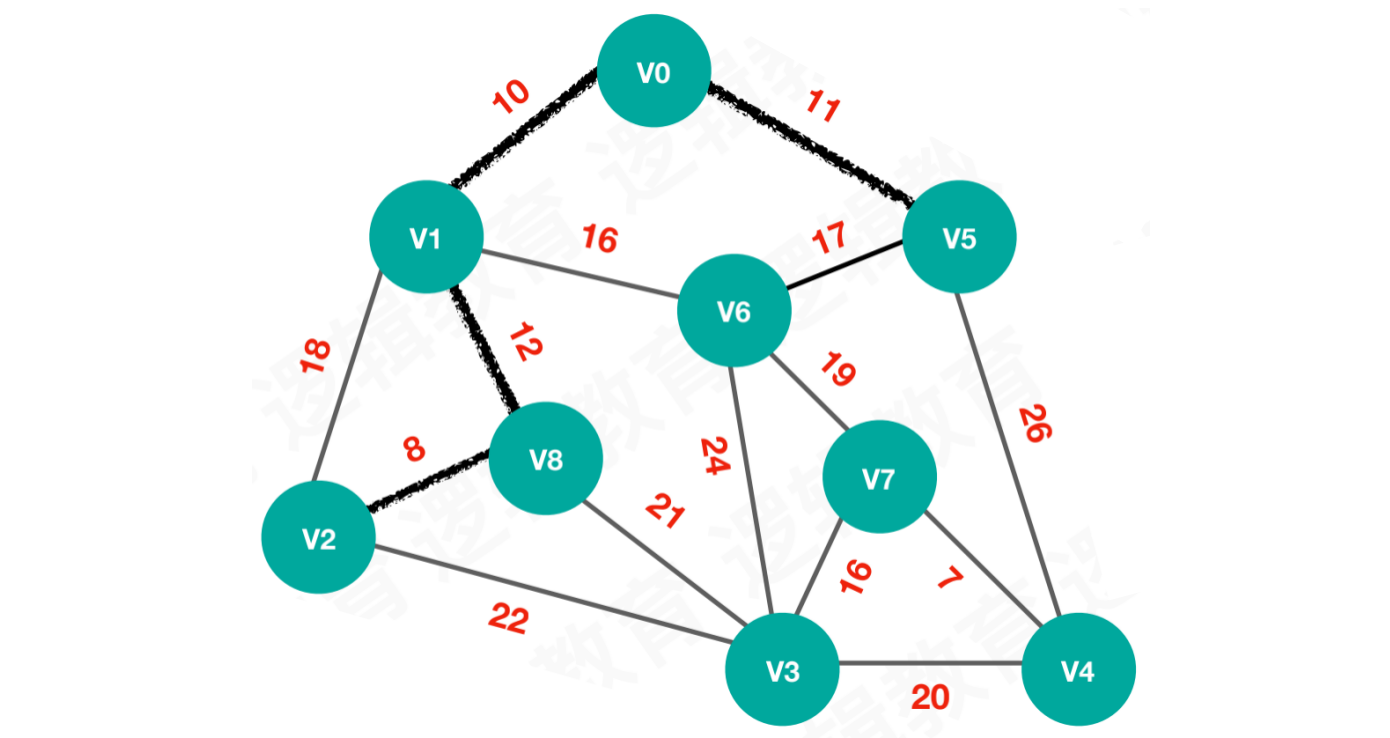
【步骤五】待选择的路线为17、26、16、21、22,选择路线16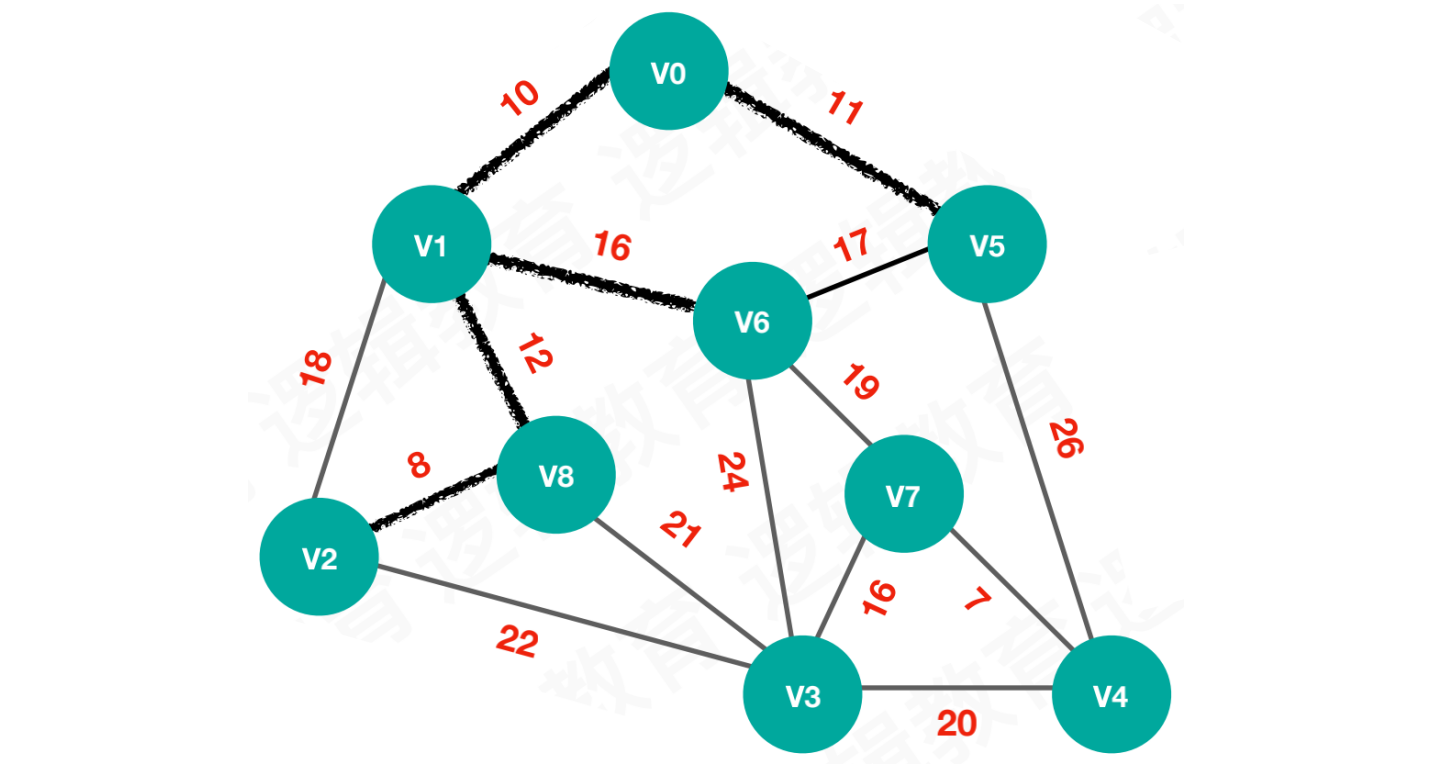
【步骤六】待选择的路线为26、21、22、24、19,选择路线19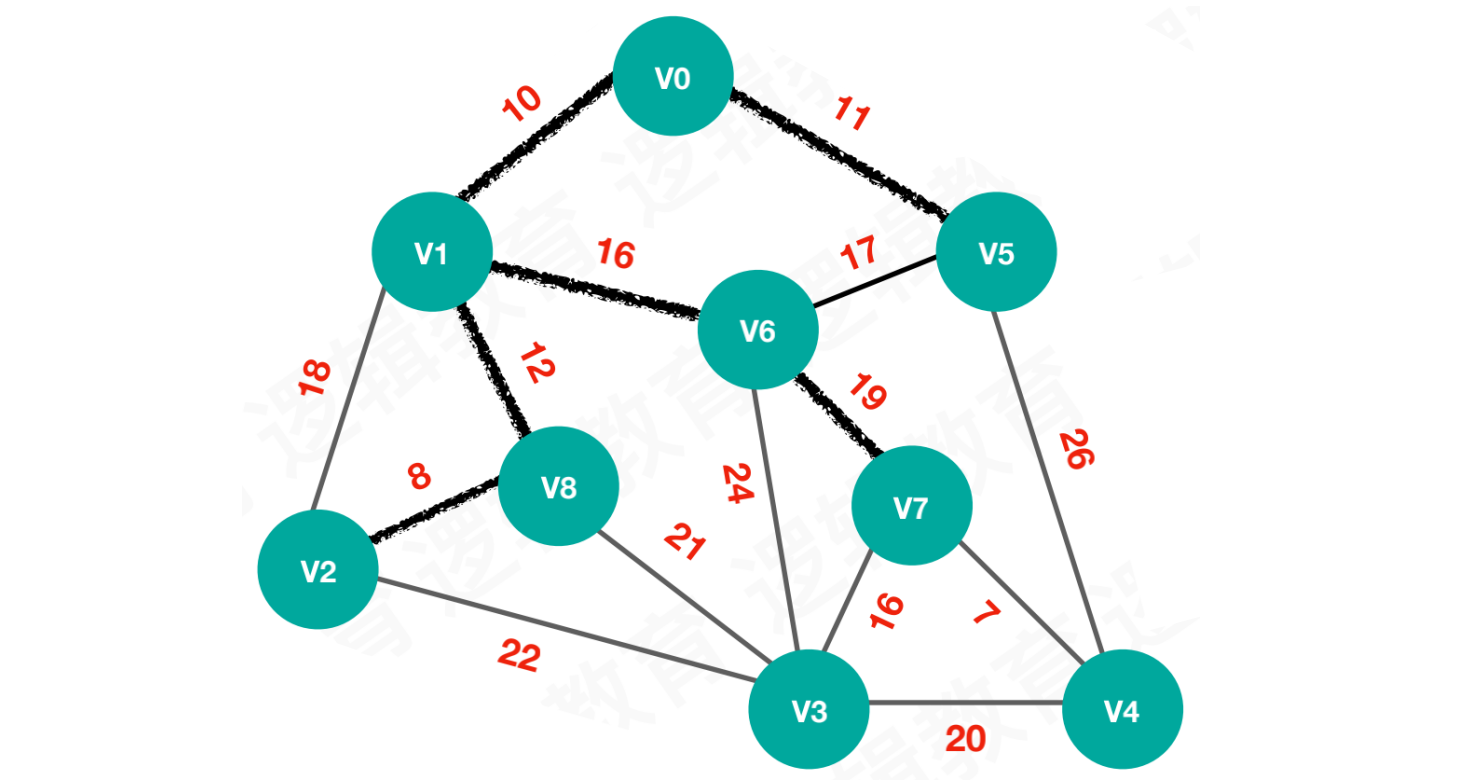
【步骤七】待选择的路线为26、21、22、24、16、7,选择路线7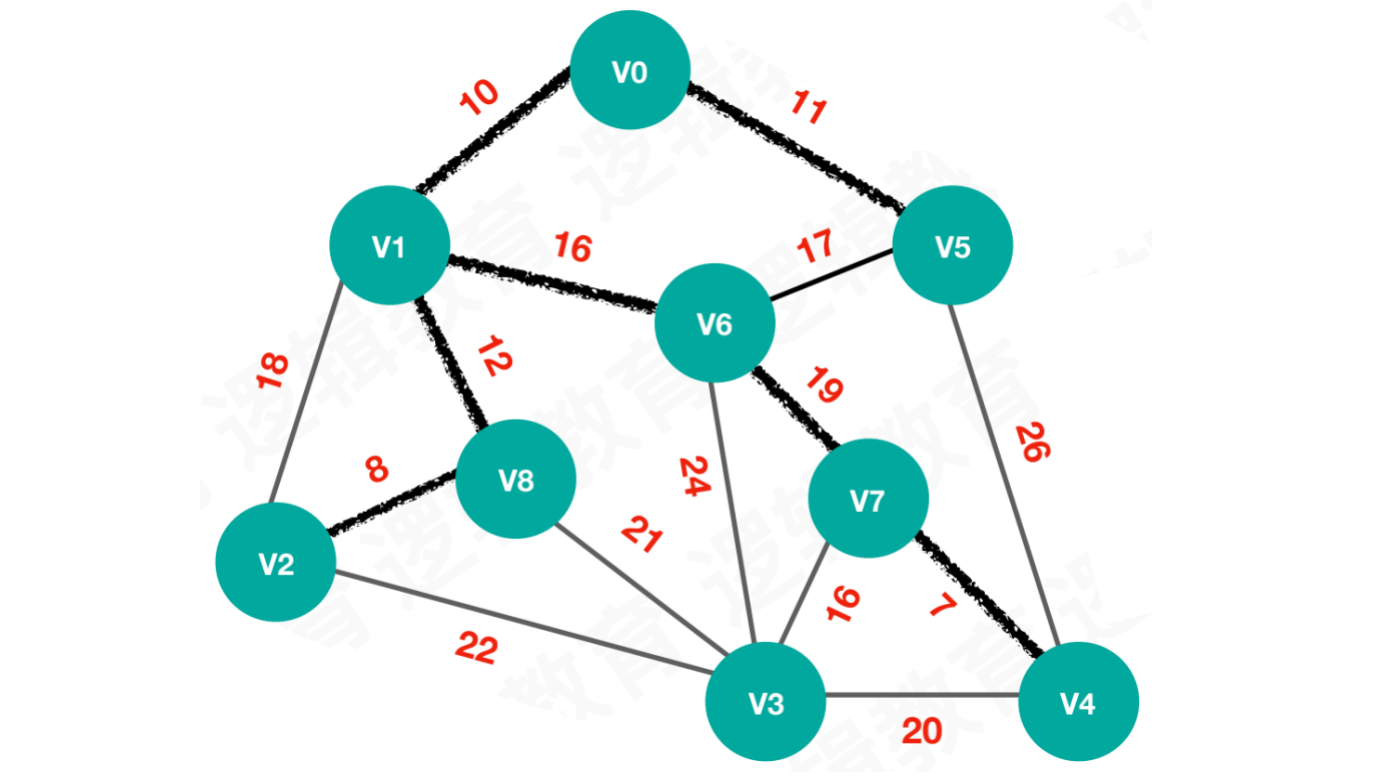
【步骤八】待选择的路线为21、22、24、16、20,选择路线16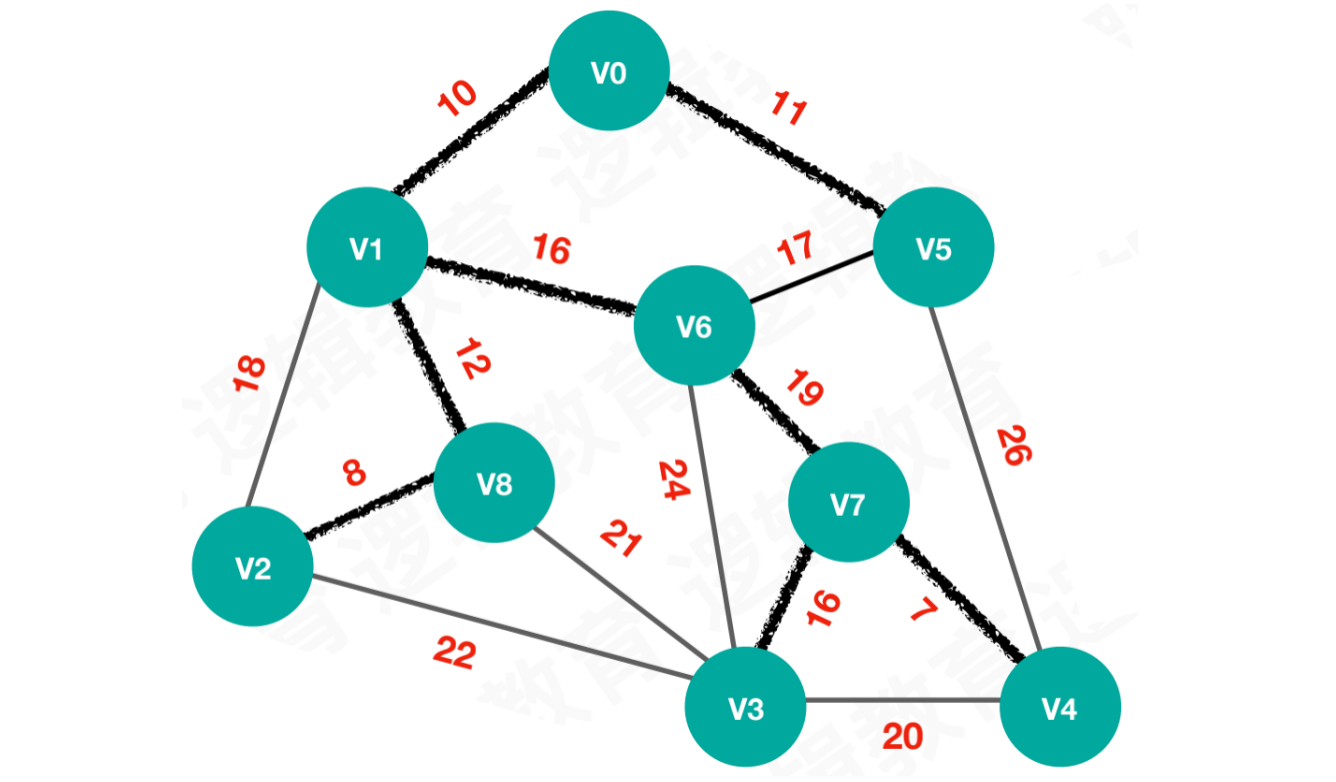
此时,所有顶点都已加入最小生成树。不难看出,Prim算法比较随性,选择路线走一步看一步。它会从当前的所用通路中,选择一个权值最小的边连接下一个顶点,直到连接所有顶点为止。在寻址路线的过程中,避免顶点之间形成闭环
2.1 算法思路
定义两个一维数组,
adjvex⽤来保存相关顶点下标,lowcost保存顶点之间的权值初始化两个数组,从
v0开始寻找最⼩⽣成树。默认v0是最⼩⽣成树上第⼀个顶点循环
lowcost数组,根据权值找到顶点k更新
lowcost数组循环所有顶点,找到与
顶点k有关系的顶点,并更新lowcost数组与adjvex数组。符合以下条件则更新:与
顶点k之间有连接当前
结点j没有加⼊过最⼩⽣成树顶点k与当前顶点j之间的权值,⼩于顶点j与其他顶点k之前的权值,则更新。简单说:就是要⽐较之前存储的值要⼩,则更新
2.2 算法分析
首先将网图使用邻接矩阵存储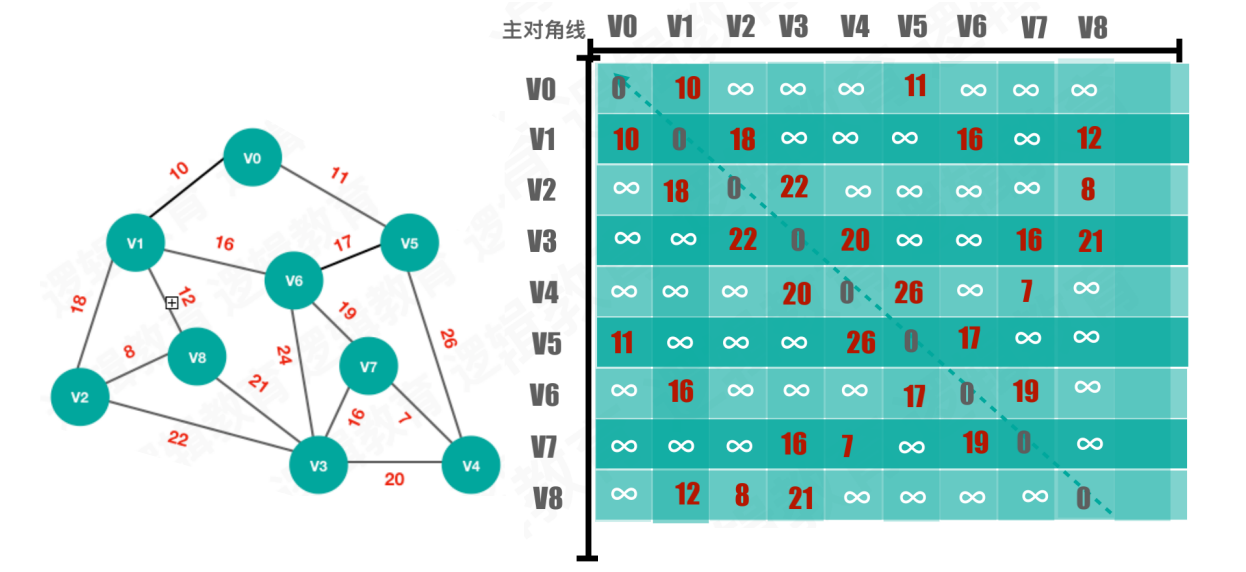
【初始准备】按照顶点总数,初始化lowcost和adjvex数组,将V0加入最小生成树
lowcost = [0, max, max, max, max, max, max, max, max]adjvex = [0, 0 ,0, 0, 0, 0, 0, 0, 0]
数组
lowcost,默认使用Int.max填充将
adjvex数组中所有元素初始化为0,假设所有顶点都和V0有关联由于
V0加入最小生成树,所以lowcost[0] = 0
将V0关联的顶点所对应的权值更新到lowcost中
lowcost = [0, 10, max, max, max, 11, max, max, max]adjvex = [0, 0 ,0, 0, 0, 0, 0, 0, 0]
和
V0有关系的顶点是V1和V5,将它们对应的权值更新到lowcost中,并将V0的索引值更新到adjvex中lowcost[1] = 10,lowcost[5] = 11adjvex[1] = 0,adjvex[5] = 0
【第一次执行】将最小权值10的顶点V1加入最小生成树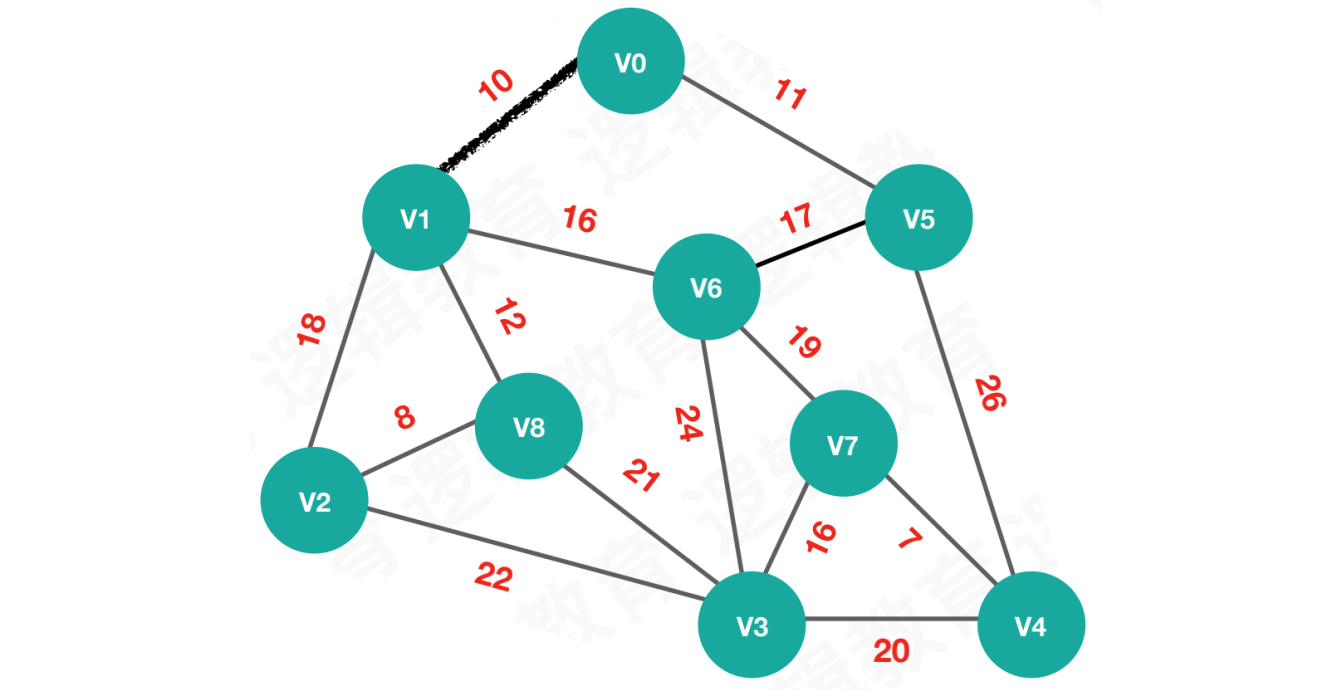
执行结果:
lowcost = [0, 0, 18, max, max, 11, 16, max, 12]adjvex = [0, 0 ,1, 0, 0, 0, 1, 0, 1]
由于
V1加入最小生成树,所以lowcost[1] = 0和
V1有关系的顶点是V2、V6、V8,将它们对应的权值更新到lowcost中,并将V1的索引值更新到adjvex中lowcost[2] = 18,lowcost[6] = 16,lowcost[8] = 12adjvex[2] = 1,adjvex[6] = 1,adjvex[8] = 1
【第二次执行】将最小权值11的顶点V5加入最小生成树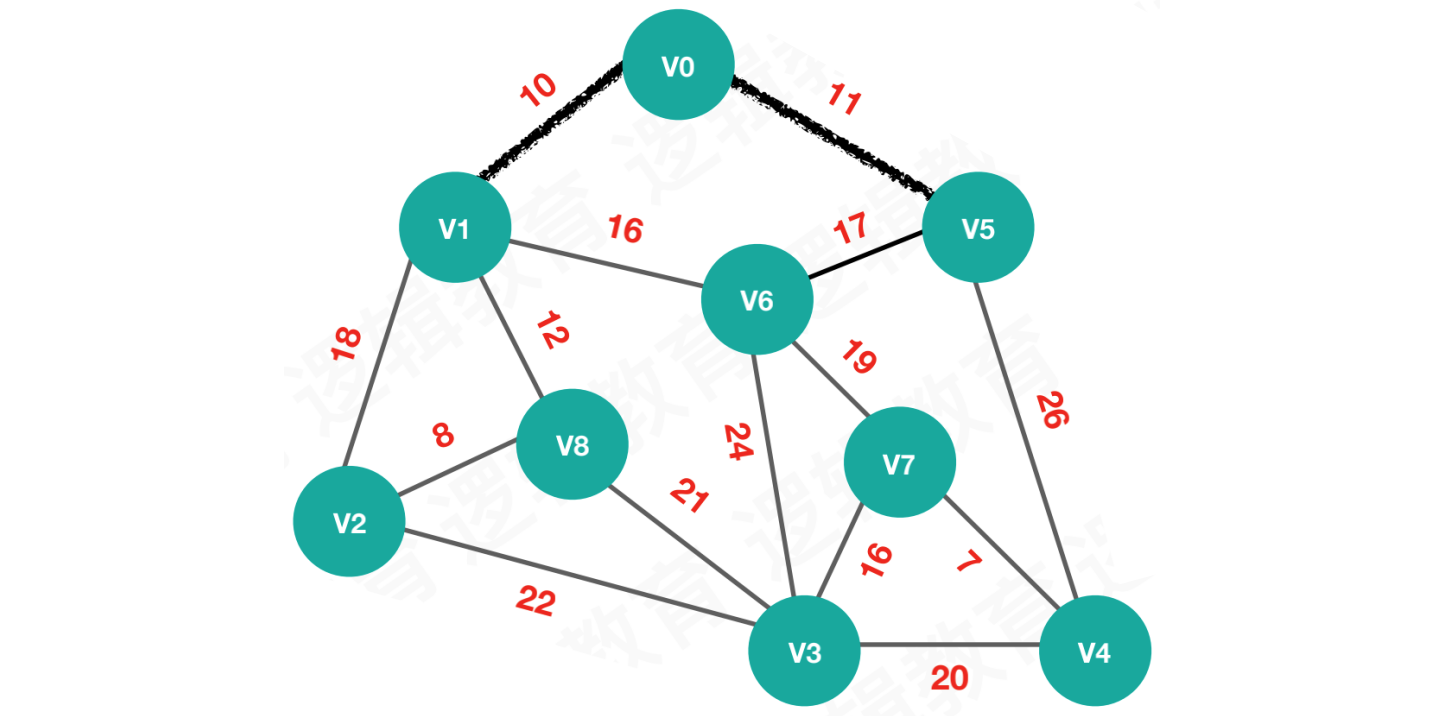
执行结果:
lowcost = [0, 0, 18, max, 26, 0, 16, max, 12]
adjvex = [0, 0 ,1, 0, 5, 0, 1, 0, 1]
由于
V5加入最小生成树,所以lowcost[5] = 0和
V5有关系的顶点是V4、V6,但此时V6和V1也有关联,并且和V1的权值更小。所以只将V4的权值更新到lowcost中,并将V5的索引值更新到adjvex中lowcost[4] = 26adjvex[4] = 5
【第三次执行】将最小权值12的顶点V8加入最小生成树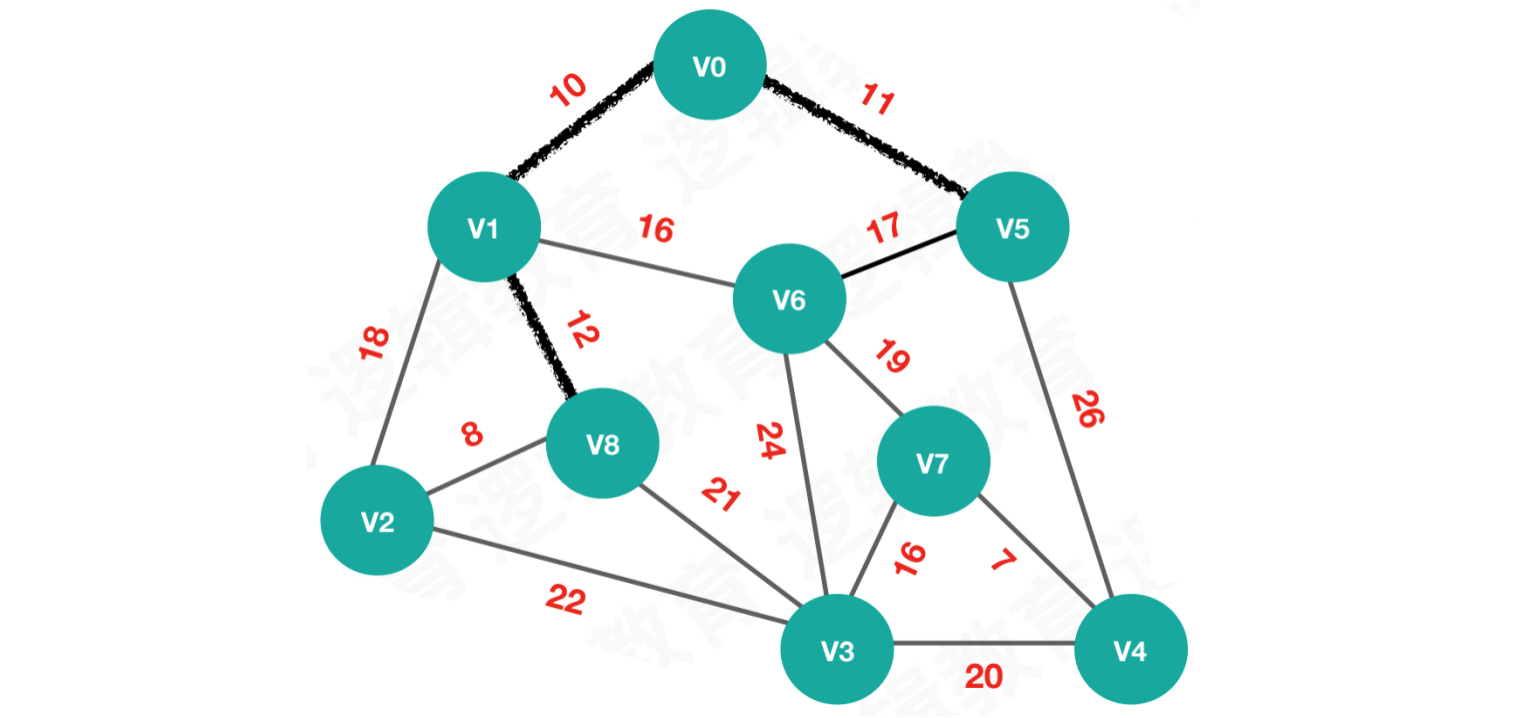
执行结果:
lowcost = [0, 0, 8, 21, 26, 0, 16, max, 0]
adjvex = [0, 0 ,8, 8, 5, 0, 1, 0, 1]
由于
V8加入最小生成树,所以lowcost[8] = 0和
V8有关系的顶点是V2、V3,虽然V2和V1也有关联,但V2和V8的权值更小。所以将它们对应的权值更新到lowcost中,并将V8的索引值更新到adjvex中lowcost[2] = 8,lowcost[3] = 21adjvex[2] = 8,adjvex[3] = 8
【第四次执行】将最小权值8的顶点V2加入最小生成树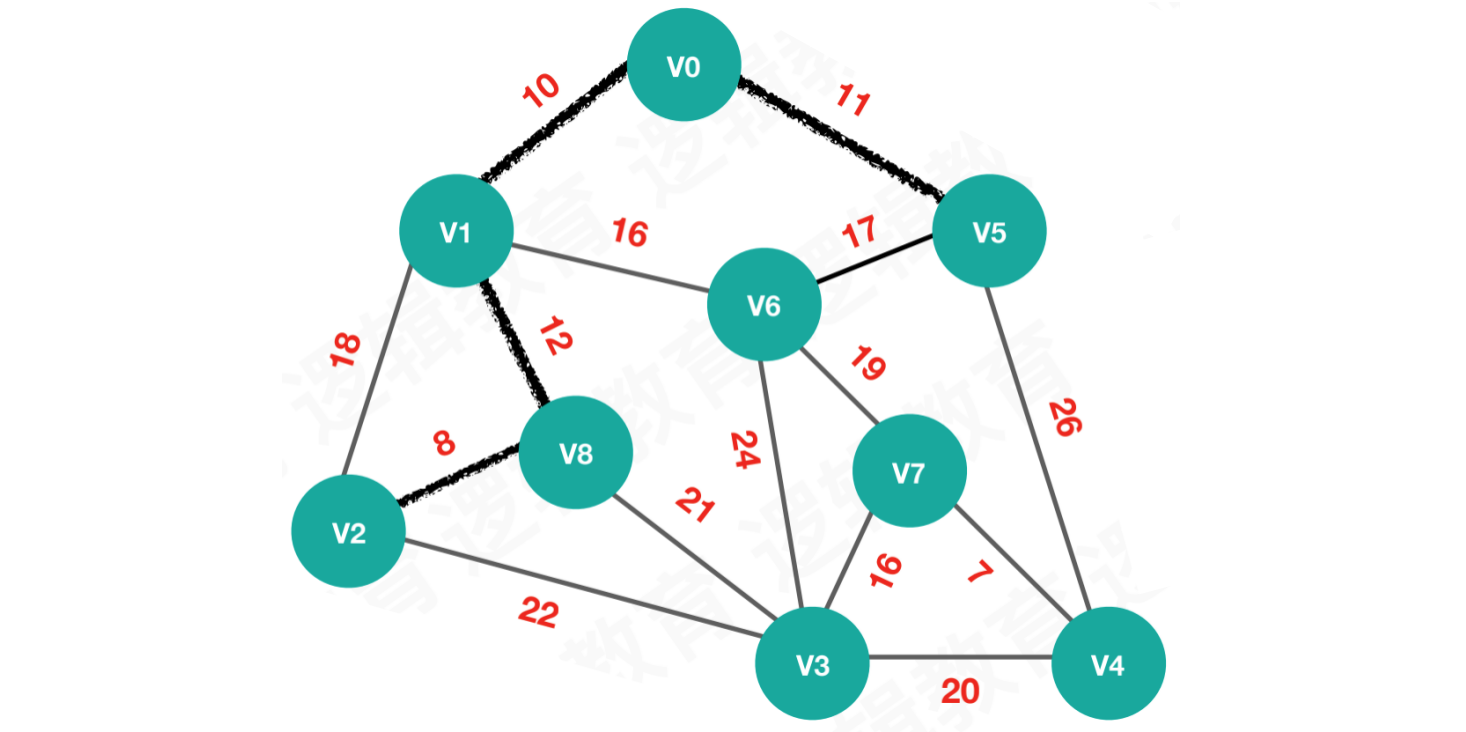
执行结果:
lowcost = [0, 0, 0, 21, 26, 0, 16, max, 0]
adjvex = [0, 0 ,8, 8, 5, 0, 1, 0, 1]
由于
V2加入最小生成树,所以lowcost[2] = 0和
V2有关系的顶点是V3,但V3和V8的权值更小,所以本次没有要更新的权值和索引值
【第五次执行】将最小权值16的顶点V6加入最小生成树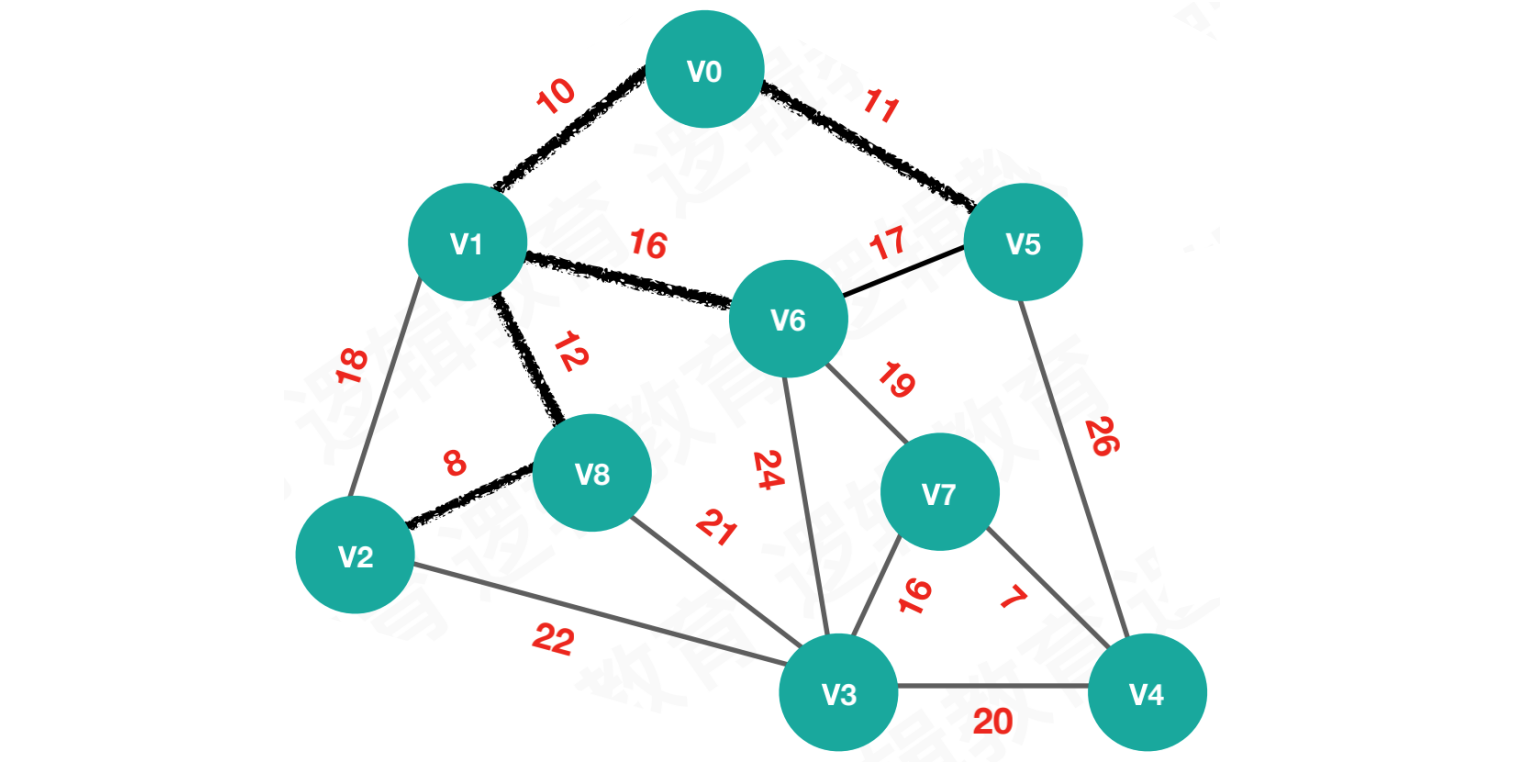
执行结果:
lowcost = [0, 0, 0, 21, 26, 0, 0, 19, 0]
adjvex = [0, 0 ,8, 8, 5, 0, 1, 6, 1]
由于
V6加入最小生成树,所以lowcost[6] = 0和
V6有关系的顶点是V3、V5、V7,但V3和V8的权值更小,而V5已加入最小生成树。所以只将V7的权值更新到lowcost中,并将V6的索引值更新到adjvex中lowcost[7] = 19adjvex[7] = 6
【第六次执行】将最小权值19的顶点V7加入最小生成树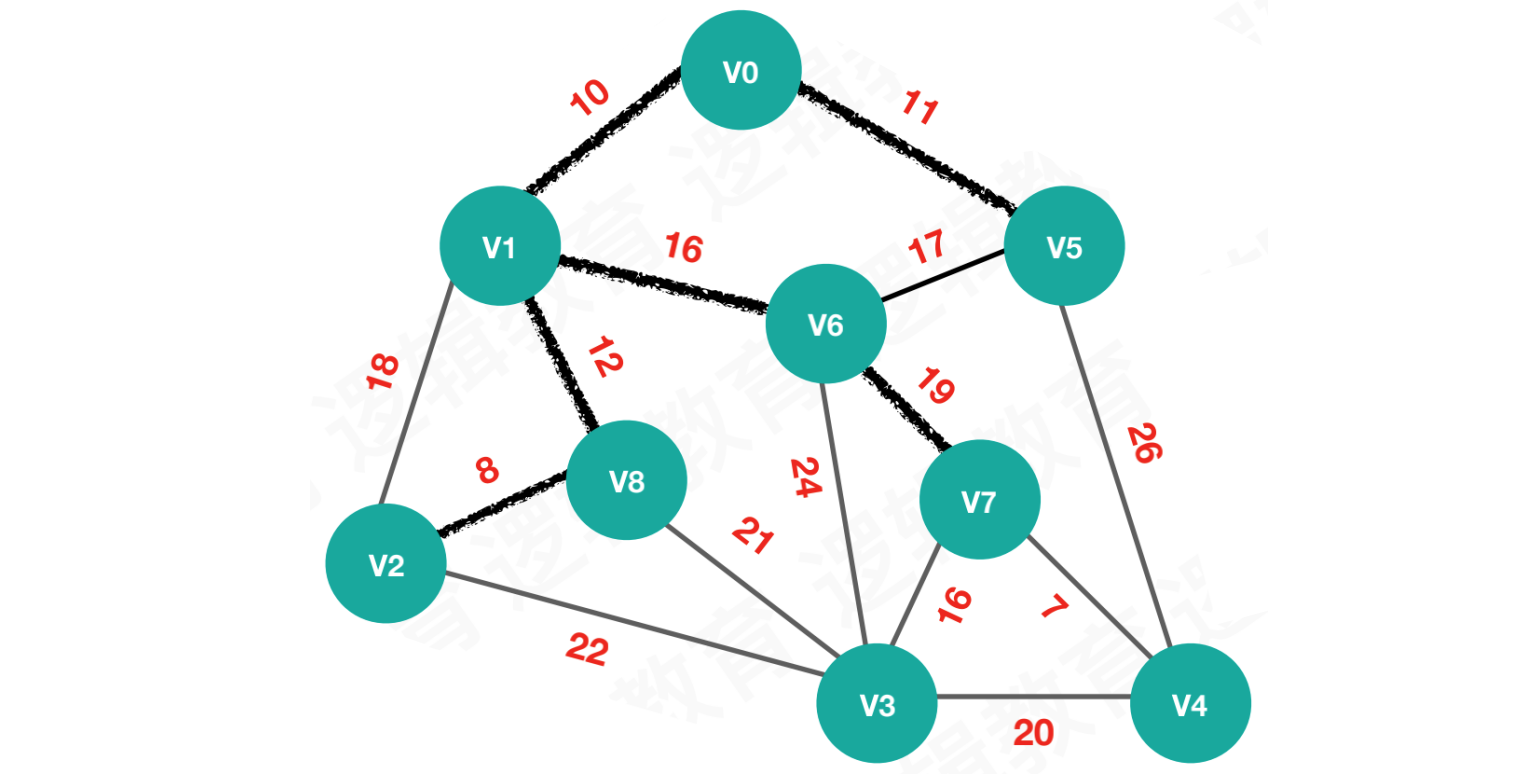
执行结果:
lowcost = [0, 0, 0, 16, 7, 0, 0, 0, 0]
adjvex = [0, 0 ,8, 7, 7, 0, 1, 6, 1]
由于
V7加入最小生成树,所以lowcost[7] = 0和
V7有关系的顶点是V3、V4,由于V3、V4和V7的权值更小,所以将它们对应的权值更新到lowcost中,并将V7的索引值更新到adjvex中lowcost[3] = 16,lowcost[4] = 7lowcost[3] = 7,lowcost[4] = 7
【第七次执行】将最小权值7的顶点V4加入最小生成树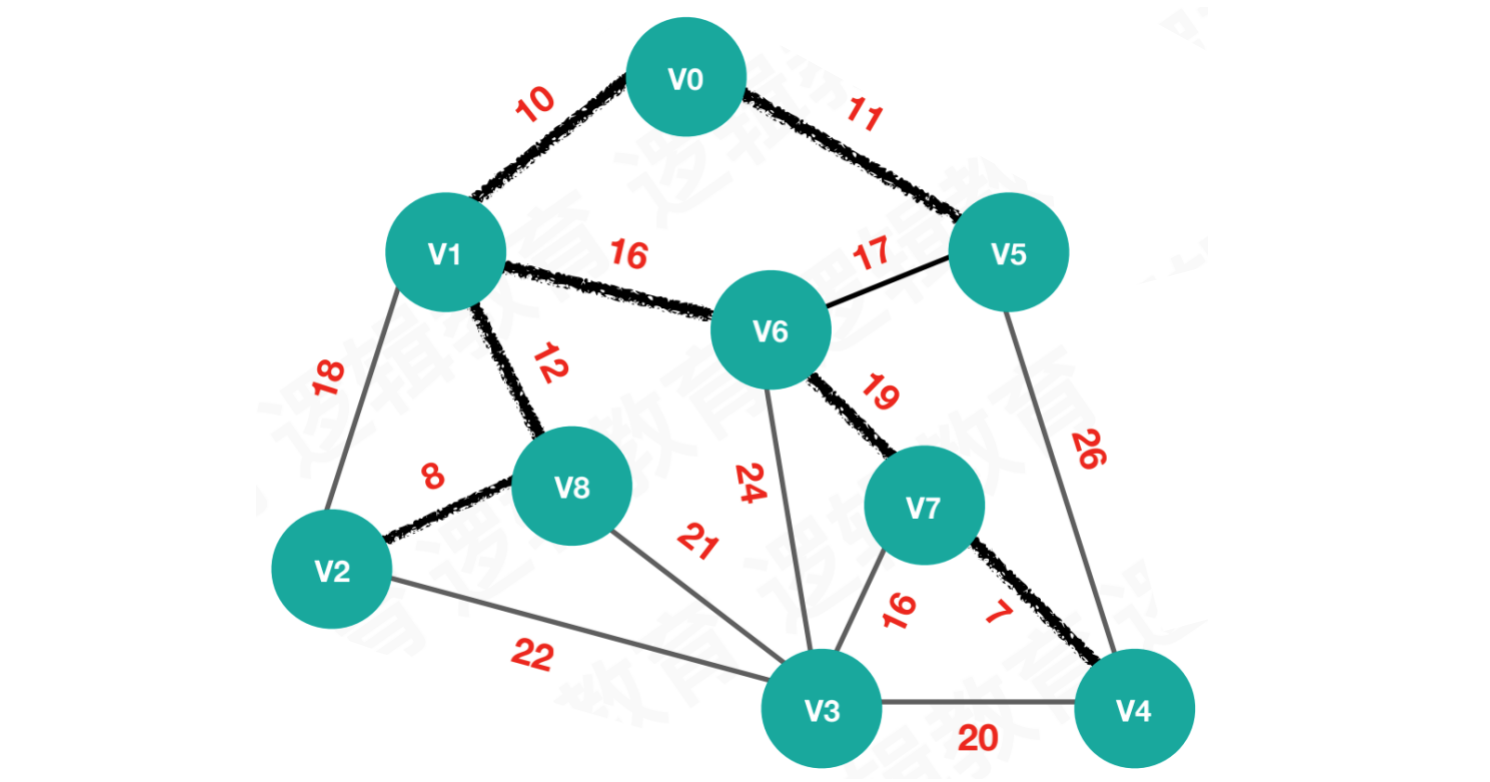
执行结果:
lowcost = [0, 0, 0, 16, 0, 0, 0, 0, 0]
adjvex = [0, 0 ,8, 7, 7, 0, 1, 6, 1]
由于
V7加入最小生成树,所以lowcost[7] = 0和
V7有关系的顶点是V3、V5,但V3和V7的权值更小,而V5已加入最小生成树,所以本次没有要更新的权值和索引值
【第八次执行】将最小权值16的顶点V3加入最小生成树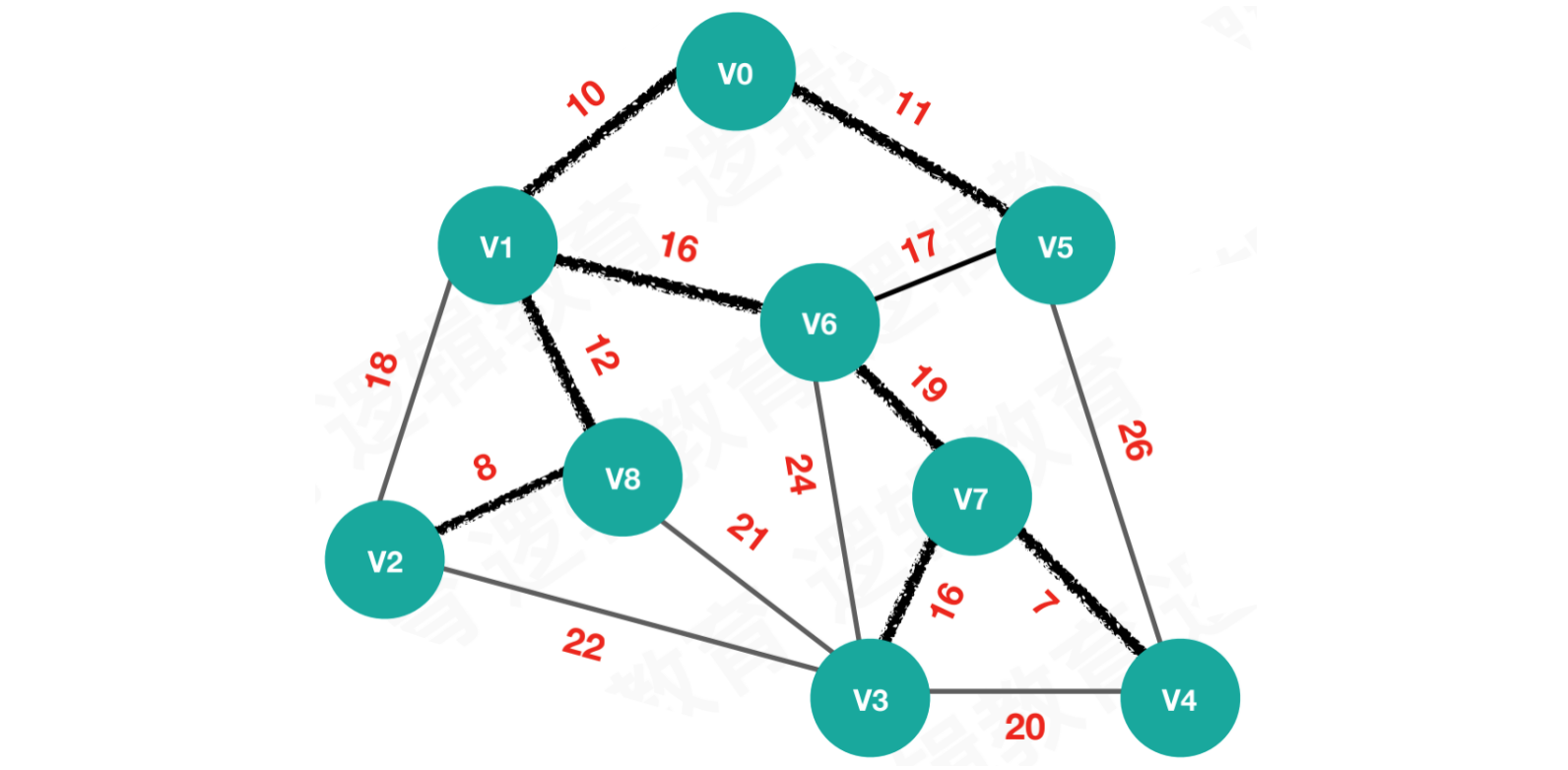
执行结果:
lowcost = [0, 0, 0, 0, 0, 0, 0, 0, 0]
adjvex = [0, 0 ,8, 7, 7, 0, 1, 6, 1]
由于
V3加入最小生成树,所以lowcost[3] = 0由于所有的顶点都已加入最小生成树,所以程序执行结束
2.3 代码实现
延用“邻接矩阵存储”的案例代码,修改MGraphLinear类中代码
创建方法增加入参,支持网图的创建
class MGraphLinear {
func create(nodes : [String], edges : [[Int]], isUndirected : Bool, isNet : Bool){
self.graph.numNodes = nodes.count;
self.graph.numEdges = edges.count;
self.graph.vexs = [String]();
for node in nodes {
self.graph.vexs?.append(node);
}
if(isNet){
createNet(edges: edges, isUndirected: isUndirected);
}
else {
createGraph(edges: edges, isUndirected: isUndirected);
}
}
fileprivate func createGraph(edges : [[Int]], isUndirected : Bool) {
self.graph.arc = [[Int]].init(repeating: [Int].init(repeating: 0, count: self.graph.numNodes), count: self.graph.numNodes);
for edge in edges {
let i = edge[0];
let j = edge[1];
let w = edge[2];
self.graph.arc![i][j] = w;
if(isUndirected){
self.graph.arc![j][i] = self.graph.arc![i][j];
}
}
}
fileprivate func createNet(edges : [[Int]], isUndirected : Bool) {
self.graph.arc = [[Int]].init(repeating: [Int].init(repeating: Int.max, count: self.graph.numNodes), count: self.graph.numNodes);
for i in 0 ..< self.graph.numNodes {
self.graph.arc![i][i] = 0;
}for i in 0 ..< self.graph.vexs!.count {
self.graph.arc![i][i] = 0;
}
for edge in edges {
let i = edge[0];
let j = edge[1];
let w = edge[2];
self.graph.arc![i][j] = w;
if(isUndirected){
self.graph.arc![j][i] = self.graph.arc![i][j];
}
}
}
}
修改邻接矩阵的打印代码:
class MGraphLinear {
func traverse() -> String {
var str : String = "";
for arr in self.graph.arc! {
for w in arr {
if(w == Int.max){
str += "∞ ";
continue
}
if(w < 10){
str += "\(w) ";
}
else{
str += "\(w) ";
}
}
str += "\n";
}
return str;
}
}
实现Prim算法:
class MGraphLinear {
var lowcost : [Int]?;
var adjvex : [Int]?;
func miniSpanTree_prim() -> String {
var str = "";
var sum_text = "";
var sum_num = 0;
// 1、初始化lowcost和adjvex
lowcost = [Int].init(repeating: Int.max, count: self.graph.numNodes);
adjvex = [Int].init(repeating: 0, count: self.graph.numNodes);
// 2、默认k为0,将V0加入最小生成树
var k = 0;
lowcost![k] = 0;
// 3、将V0的关联顶点的权值加入lowcost中
for i in 1 ..< self.graph.numNodes {
lowcost![i] = self.graph.arc![k][i];
}
// 4、循环所有顶点,由于V0已完成,所以从1开始
for _ in 1 ..< self.graph.numNodes {
var min_w = Int.max;
// 5、 循环lowcost中的权值,得到最小权重和相应的索引值。由于V0已完成,所以从1开始
for j in 1 ..< lowcost!.count {
let w = lowcost![j];
// 已加入生成树、没有连接关系、权值大于min_w,一律跳过循环
if(w == 0 || w == Int.max || w >= min_w){
continue;
}
// 得到最小权重和索引值
min_w = w;
k = j;
}
let source = self.adjvex![k];
str += "\(self.graph.vexs![source]) -> \(self.graph.vexs![k]) = \(min_w)\n";
sum_text += "\(min_w) + ";
sum_num += min_w;
// 6、将最小权值的顶点加入最小生成树
lowcost![k] = 0;
// 7、循环所有顶点,寻找k所关联的顶点。由于V0已完成,所以从1开始
for j in 1 ..< self.graph.numNodes {
let w = self.graph.arc![k][j];
// 已加入生成树、没有连接关系、权值大于lowcost中记录的权值,一律跳过循环
if(lowcost![j] == 0 || w == Int.max || lowcost![j] < w){
continue;
}
// 记录关联的顶点所对应的权值
lowcost![j] = w;
// 记录与之关联顶点的索引值
adjvex![j] = k;
}
}
sum_text = "\(sum_text.prefix(sum_text.count - 2)) = \(sum_num)";
print("Sum:\(sum_text)\n");
return str;
}
}
按照示例中的网图逻辑,使用代码创建邻接矩阵,并打印Prim算法的结果:
let nodes = ["V0", "V1", "V2", "V3", "V4", "V5", "V6", "V7", "V8"];
let edges = [[0, 1 ,10], [0, 5, 11],
[1, 2, 18], [1, 6, 16], [1, 8, 12],
[2, 3, 22], [2, 8, 8],
[3, 4, 20], [3, 6, 24], [3, 7, 16], [3, 8, 21],
[4, 5, 26], [4, 7, 7],
[5, 6, 17],
[6, 7, 19]];
let isUndirected = true;
let isNet = true;
let graphLinear = MGraphLinear();
graphLinear.create(nodes: nodes, edges: edges, isUndirected: isUndirected, isNet: isNet);
print(graphLinear.traverse());
print("\(graphLinear.miniSpanTree_prim())");
-------------------------
//输出以下内容:
0 10 ∞ ∞ ∞ 11 ∞ ∞ ∞
10 0 18 ∞ ∞ ∞ 16 ∞ 12
∞ 18 0 22 ∞ ∞ ∞ ∞ 8
∞ ∞ 22 0 20 ∞ 24 16 21
∞ ∞ ∞ 20 0 26 ∞ 7 ∞
11 ∞ ∞ ∞ 26 0 17 ∞ ∞
∞ 16 ∞ 24 ∞ 17 0 19 ∞
∞ ∞ ∞ 16 7 ∞ 19 0 ∞
∞ 12 8 21 ∞ ∞ ∞ ∞ 0
Sum:10 + 11 + 12 + 8 + 16 + 19 + 7 + 16 = 99
V0 -> V1 = 10
V0 -> V5 = 11
V1 -> V8 = 12
V8 -> V2 = 8
V1 -> V6 = 16
V6 -> V7 = 19
V7 -> V4 = 7
V7 -> V3 = 16
3 克鲁斯卡尔(Kruskal)算法
Kruskal算法特点:利用有限的连接信息,推断顶点之间是否会产生闭环
【步骤一】从最小权值7开始,连接V4和V7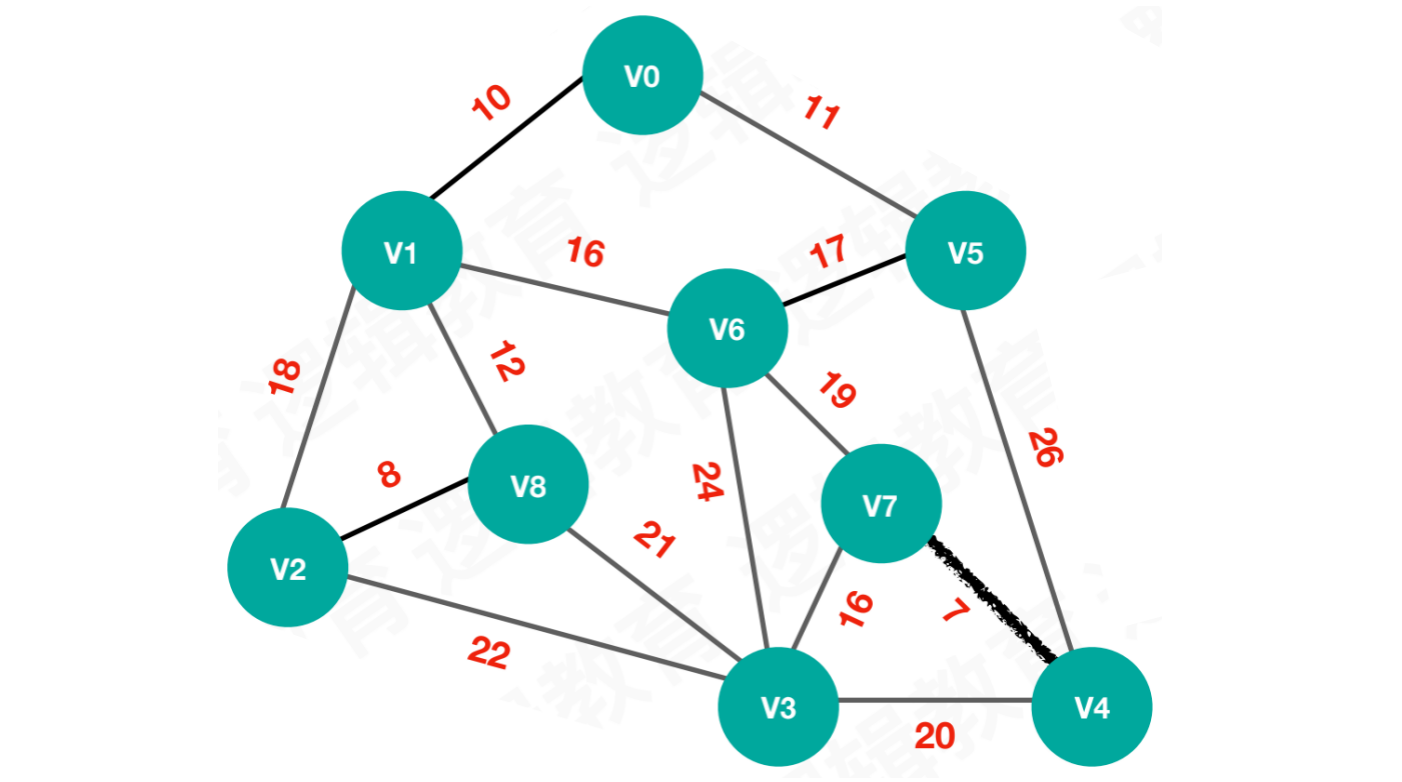
【步骤二】选择最小权值8,连接V2和V8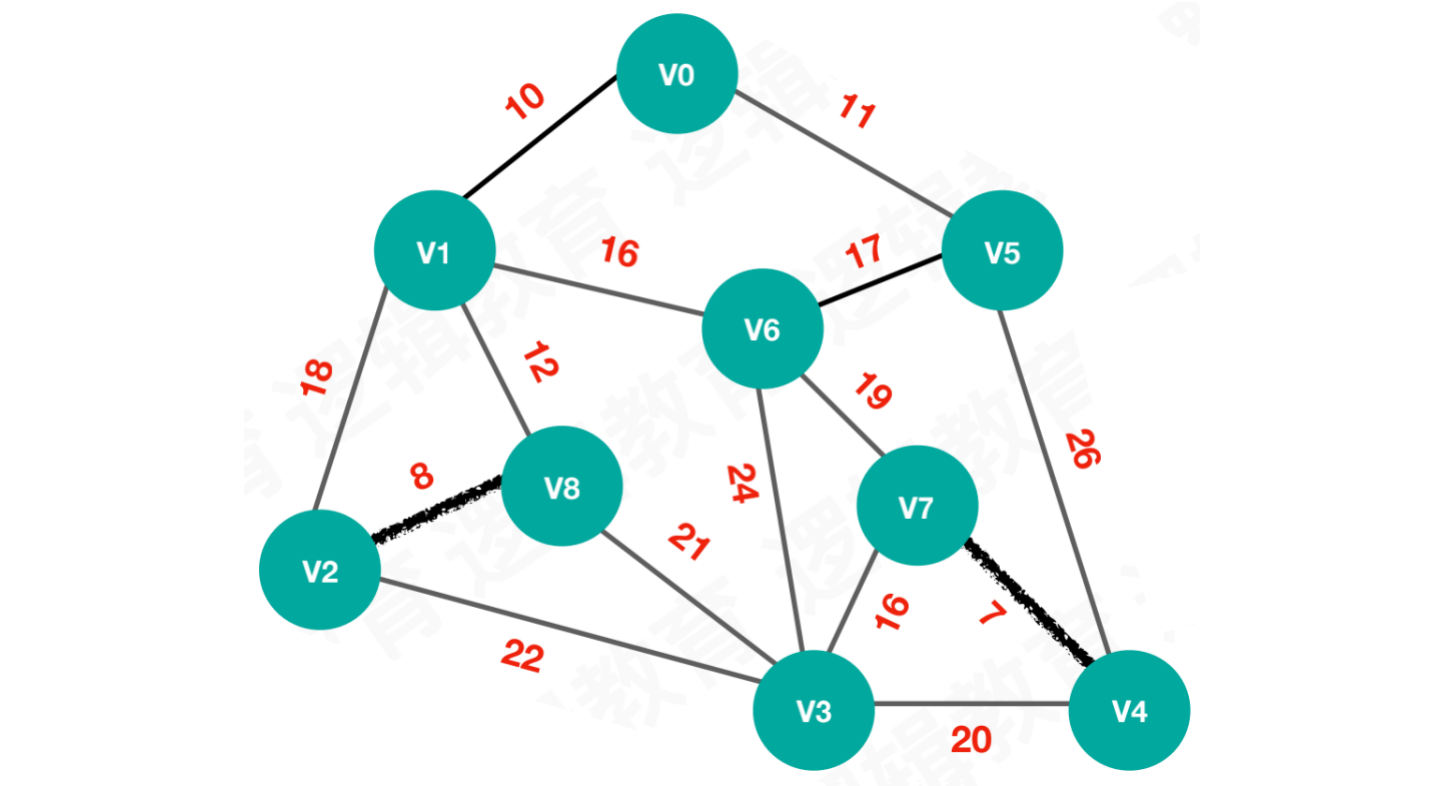
【步骤三】选择最小权值10,连接V0和V1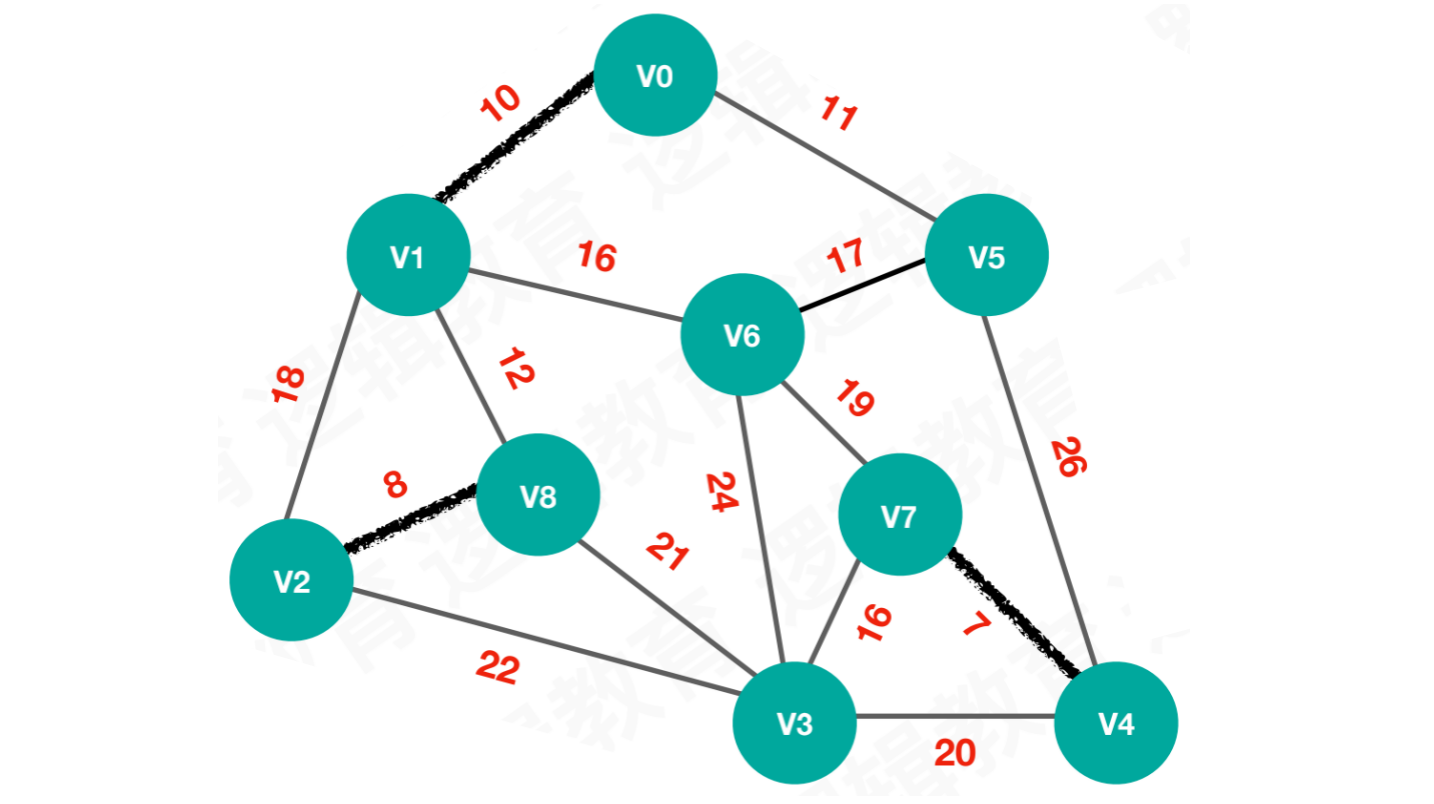
【步骤四】选择最小权值11,连接V0和V5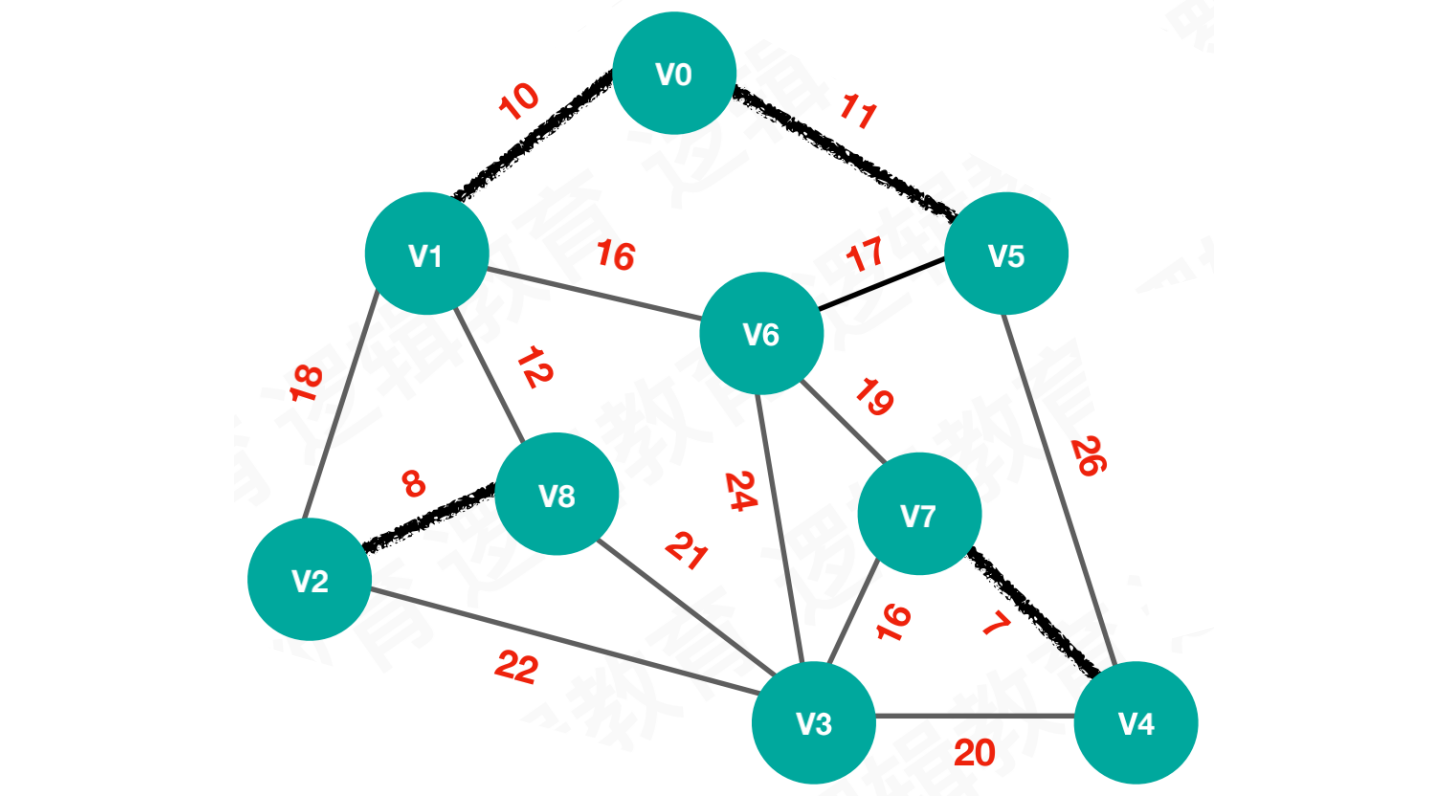
【步骤五】选择最小权值12,连接V1和V8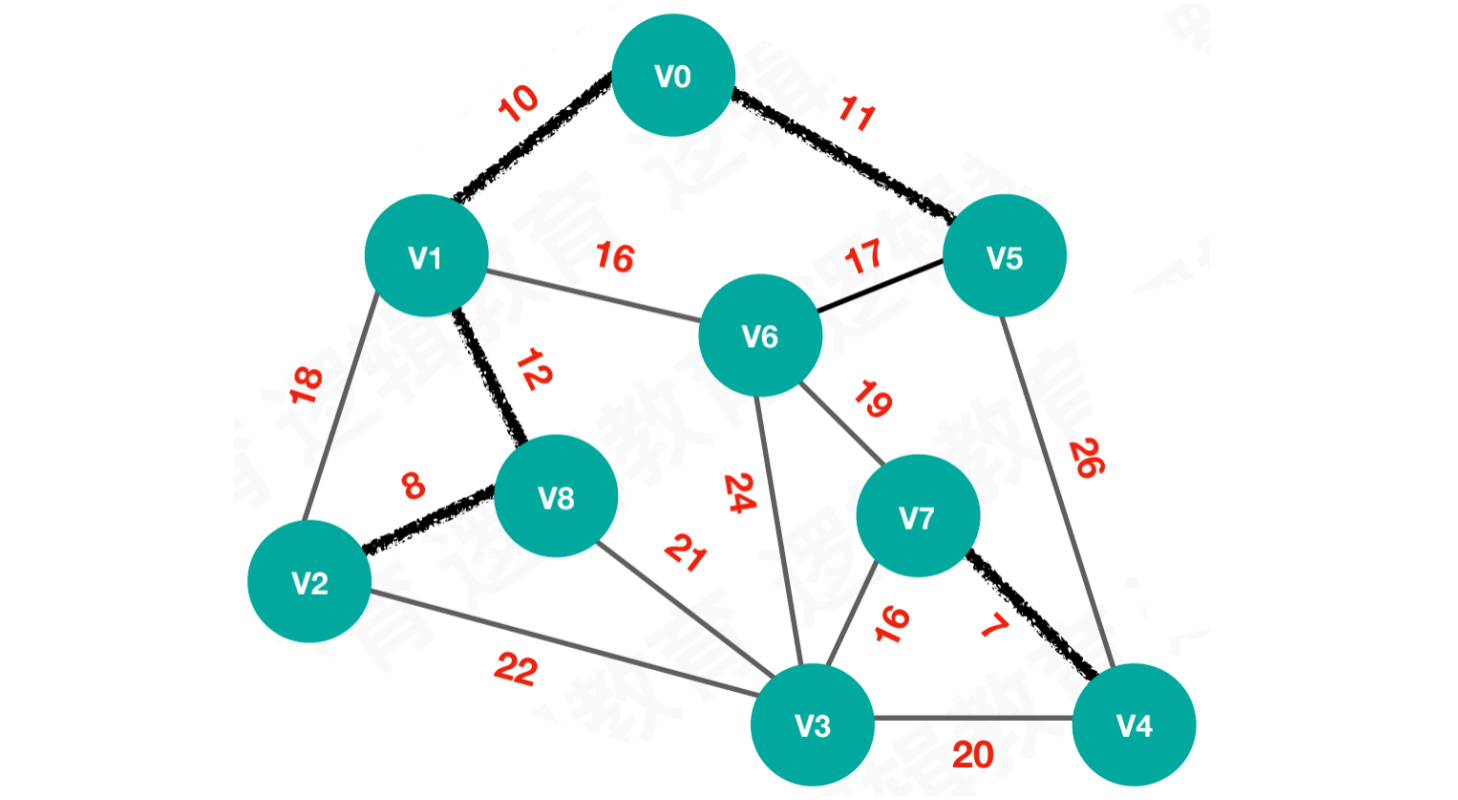
【步骤六】选择最小权值16,连接V3和V7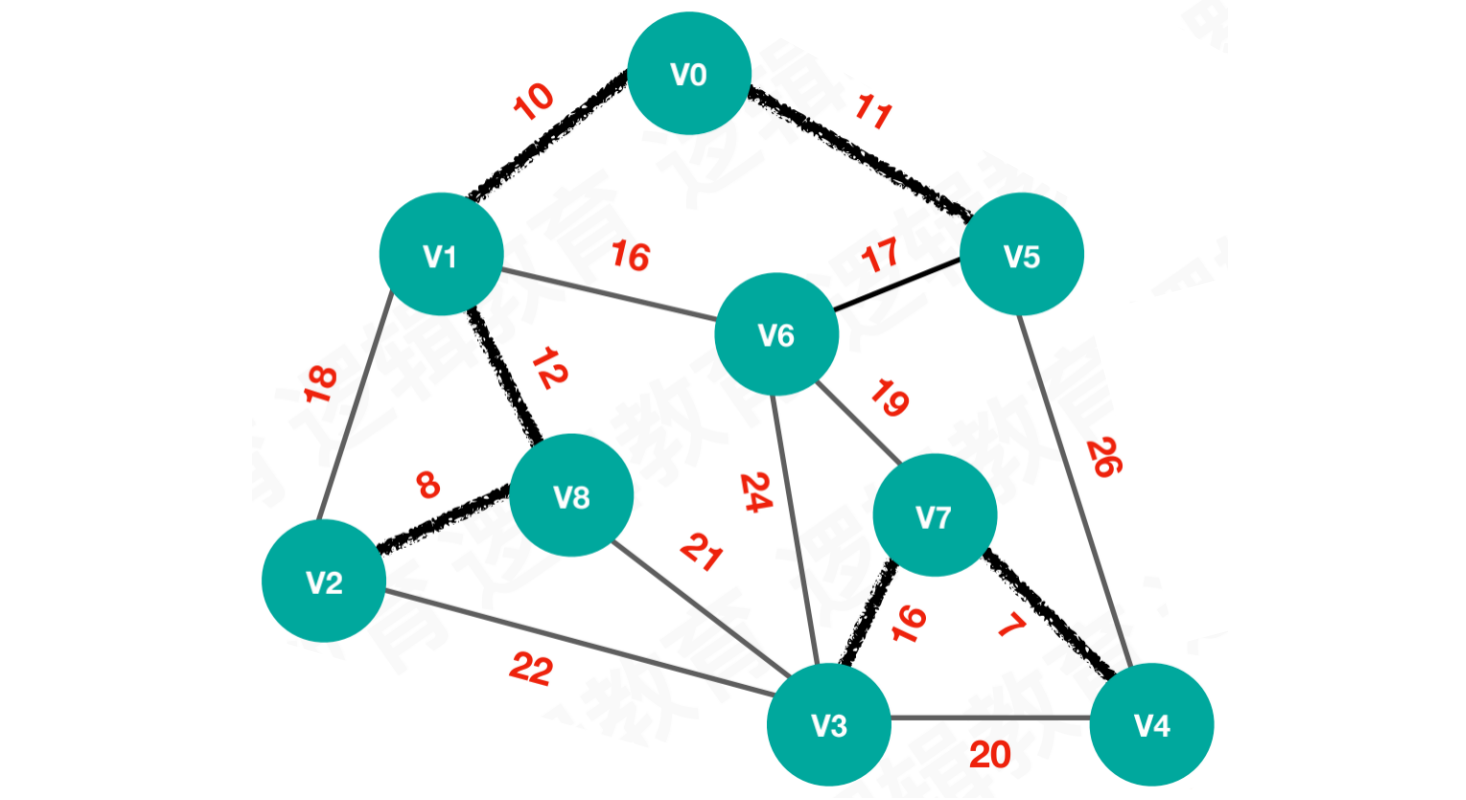
【步骤七】选择最小权值16,连接V1和V6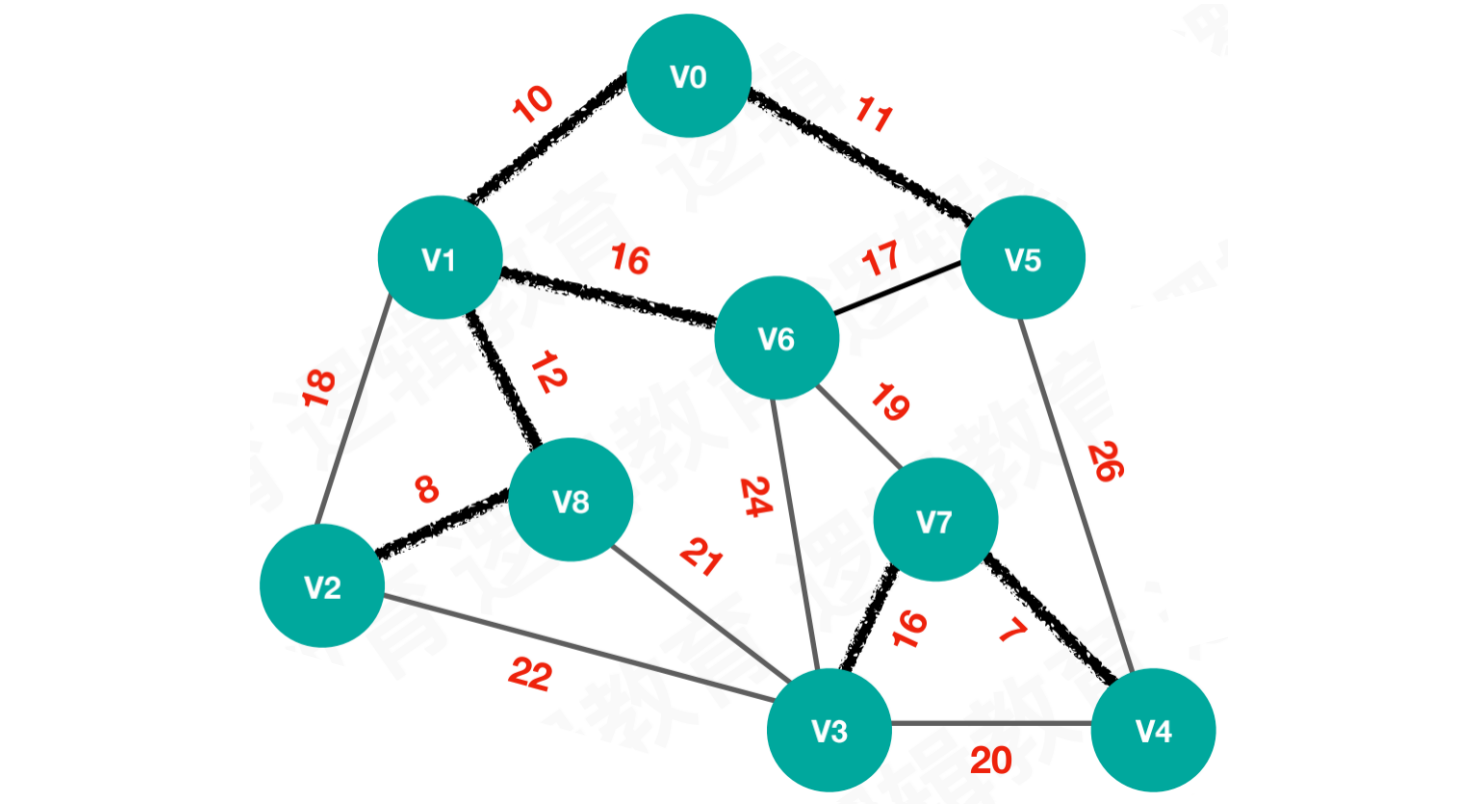
【步骤八】按照规则,应该选择最小权值17,连接V5和V6。但是在最⼩⽣成树中,边的数量等于N - 1条边,图中一定不能出现闭环。所以V5和V6不能连接
当我们跳过17,选择最小权值18,连接V1和V2,也会出现同样的问题,图中会出现闭环
因此,权值17和18只能放弃,我们选择最小权值19,连接V6和V7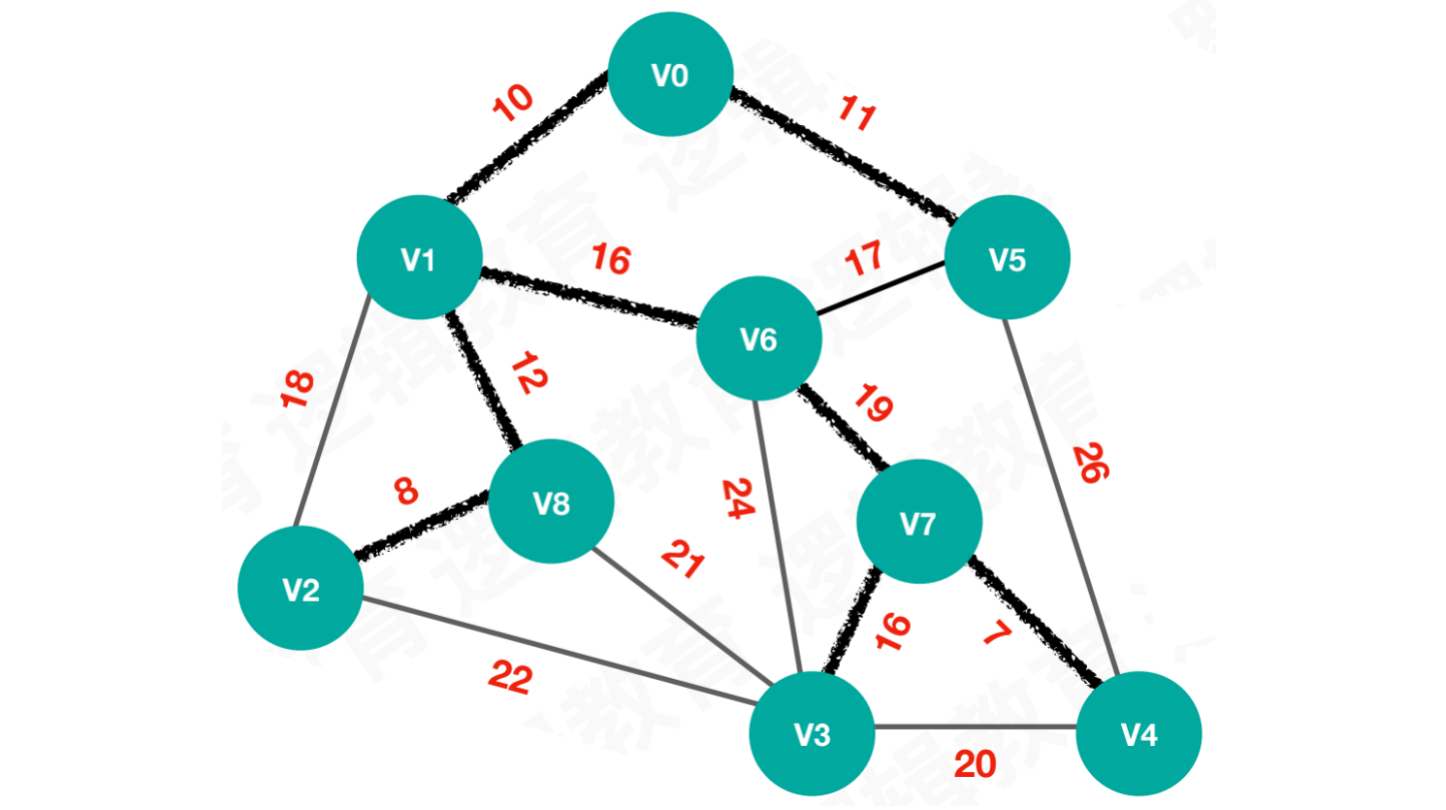
此时,所有顶点都已加入最小生成树。而剩余的五条边:V3 ~ V4、V3 ~ V8、V2 ~ V3、V3 ~ V6、V4 ~ V5,它们均不可连接。只要它们中任意一条边连接,都会使得图中形成闭环
所以Kruskal算法具有很强的规划性,它会优先选择最小权值的边,如果选择后图中不会形成闭环,即可连接它们之间的顶点
3.1 算法思路
将邻接矩阵转化成边表数组
对边表数组根据权值按照从⼩到⼤的顺序排序
遍历所有的边,通过
parent数组找到边的连接信息,避免闭环问题如果不存在闭环问题,则加⼊到最⼩⽣成树中,并且修改
parent数组
3.2 算法分析
网图的邻接矩阵: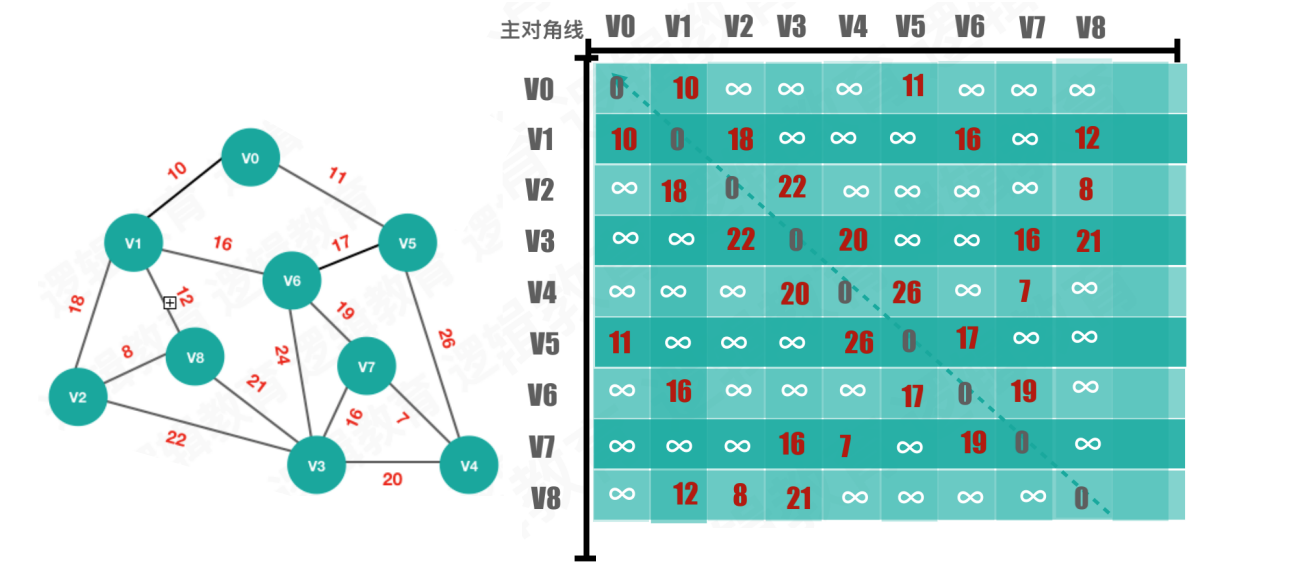
将邻接矩阵转化成边表数组:
| 边号 | begin | end | weight |
|---|---|---|---|
| edges[0] | 4 | 7 | 7 |
| edges[1] | 2 | 8 | 8 |
| edges[2] | 0 | 1 | 10 |
| edges[3] | 0 | 5 | 11 |
| edges[4] | 1 | 8 | 12 |
| edges[5] | 3 | 7 | 16 |
| edges[6] | 1 | 6 | 16 |
| edges[7] | 5 | 6 | 17 |
| edges[8] | 1 | 2 | 18 |
| edges[9] | 6 | 7 | 19 |
| edges[10] | 3 | 4 | 20 |
| edges[11] | 3 | 8 | 21 |
| edges[12] | 2 | 3 | 22 |
| edges[13] | 3 | 6 | 24 |
| edges[14] | 4 | 5 | 26 |
begin、end存储有关联的两个顶点,weight存储两点之间的权值begin存储索引值更小的顶点边表中的数据,按照权值从小到大排序
【初始准备】按照顶点总数,初始化parent 数组
parent = [0, 0, 0, 0, 0, 0, 0, 0, 0]
- 数组
parent,默认使用0填充
【第一次执行】按照edges[0],连接V4和V7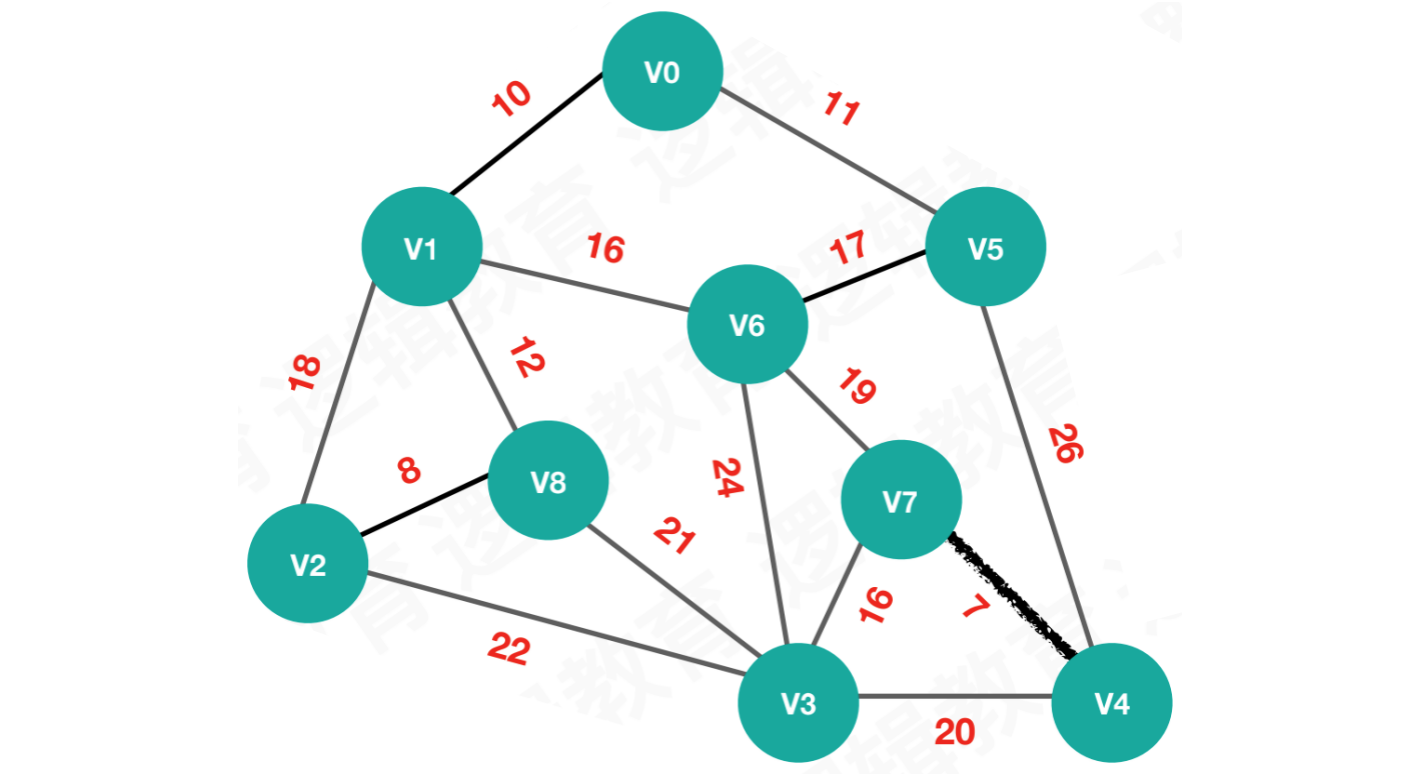
begin = 4,end = 7,weight = 7将
begin和end作为索引值,查找parent数组中的元素n = begin,当parent[n] == 0,则返回n如果
parent[n] != 0,将parent[n]的值赋值给n将
n继续作为索引值,直到查找parent[n] == 0,则返回n
m = end,如果parent[m] == 0,则返回m- 如果
parent[m] != 0,规则和n一致。遍历查找parent[m] == 0为止,返回m
- 如果
若
n != m,则parent[n] = m,表示可以将它们加⼊最⼩⽣成树若
n == m,则放弃这两个顶点,因为它们的连接会造成闭环
n = begin = 4,parent[4] == 0,则n = 4m = end = 7,parent[7] == 0,则m = 7
由于n != m,则parent[4] = 7
parent = [0, 0, 0, 0, 7, 0, 0, 0, 0]
【第二次执行】按照edges[1],连接V2和V8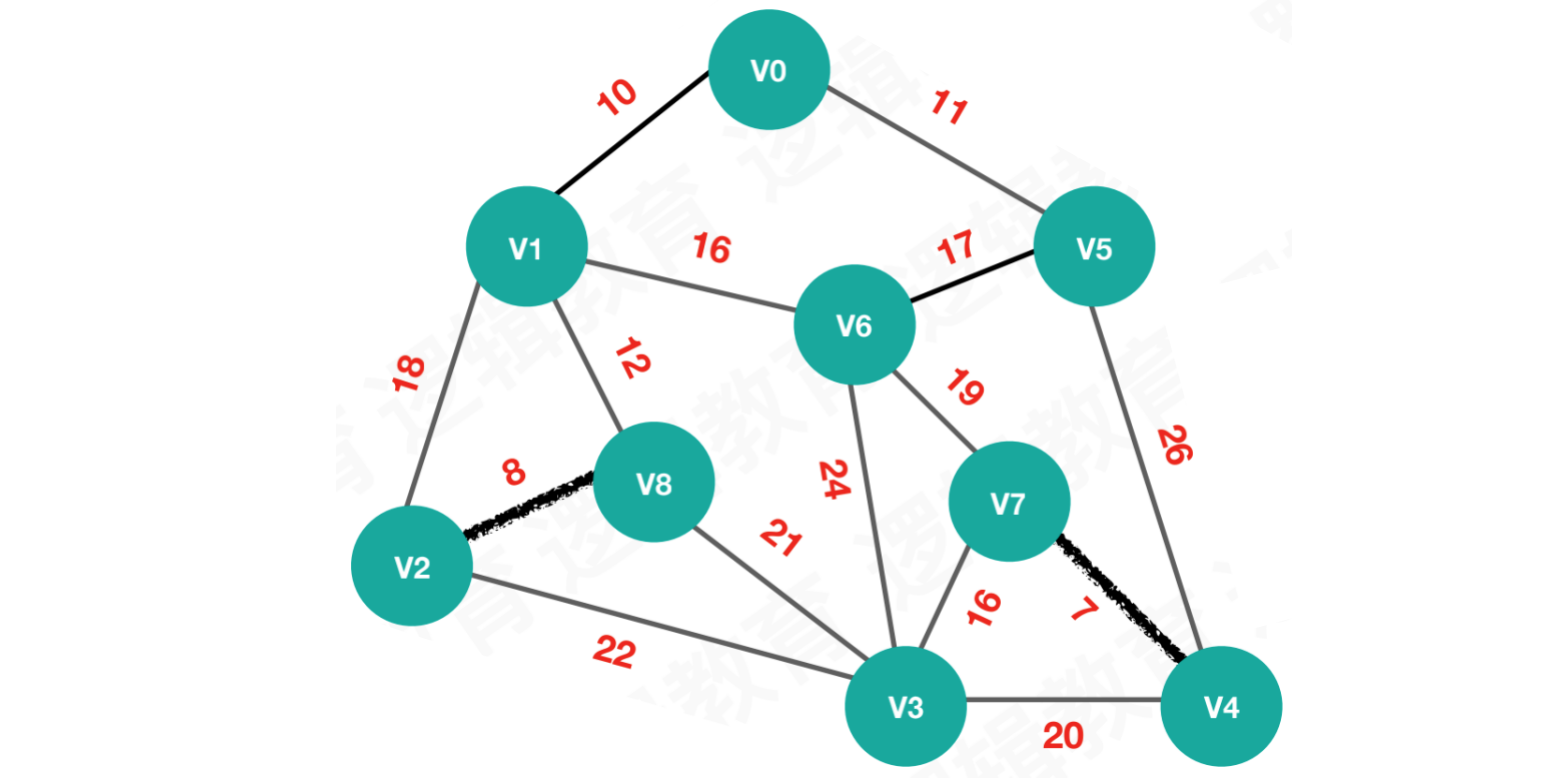
begin = 2,end = 8,weight = 8n = begin = 2,parent[2] == 0,则n = 2m = end = 8,parent[8] == 0,则m = 8
由于n != m,则parent[2] = 8
parent = [0, 0, 8, 0, 7, 0, 0, 0, 0]
【第三次执行】按照edges[2],连接V0和V1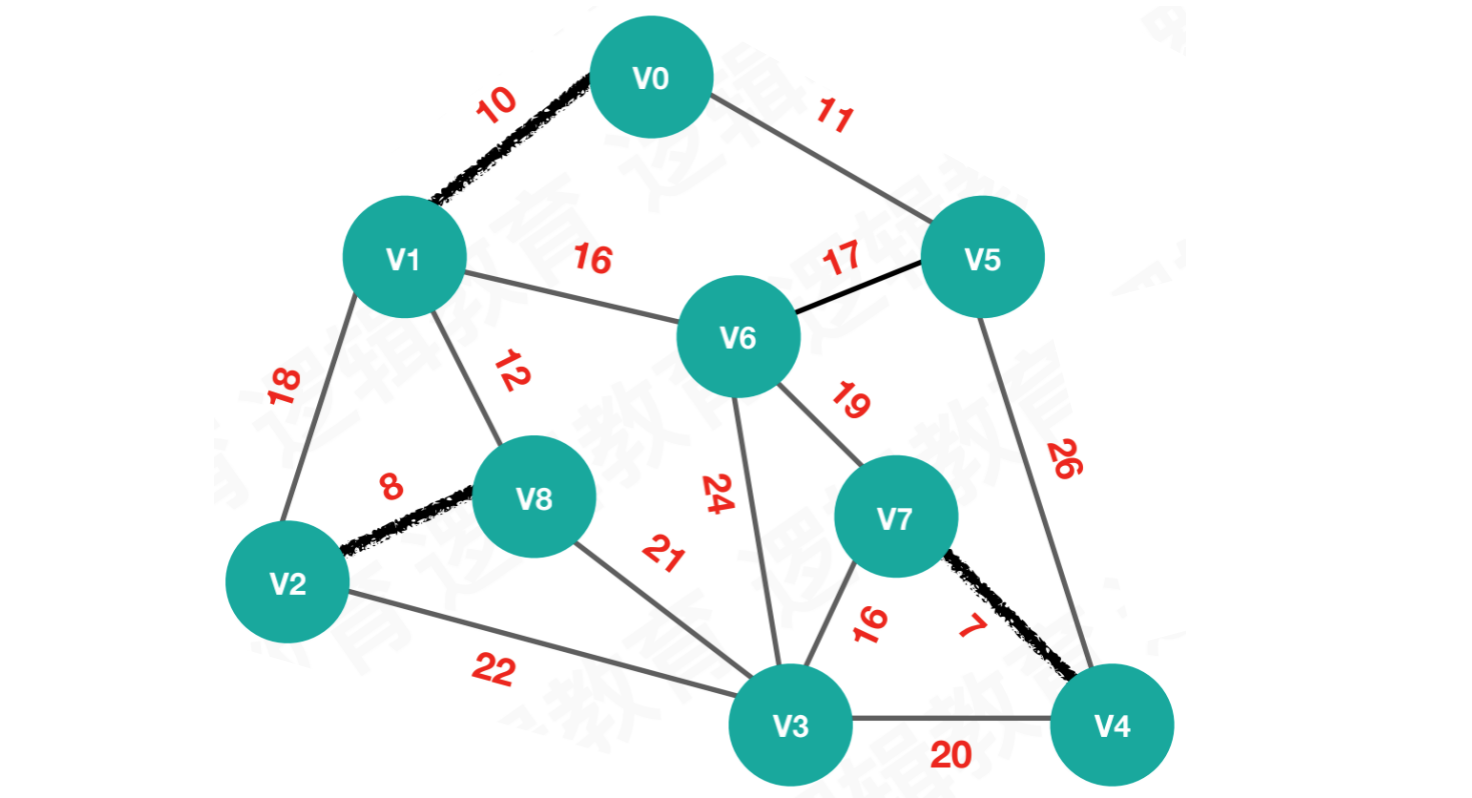
begin = 0,end = 1,weight = 10n = begin = 0,parent[0] == 0,则n = 0m = end = 1,parent[1] == 0,则m = 1
由于n != m,则parent[0] = 1
parent = [1, 0, 8, 0, 7, 0, 0, 0, 0]
【第四次执行】按照edges[3],连接V0和V5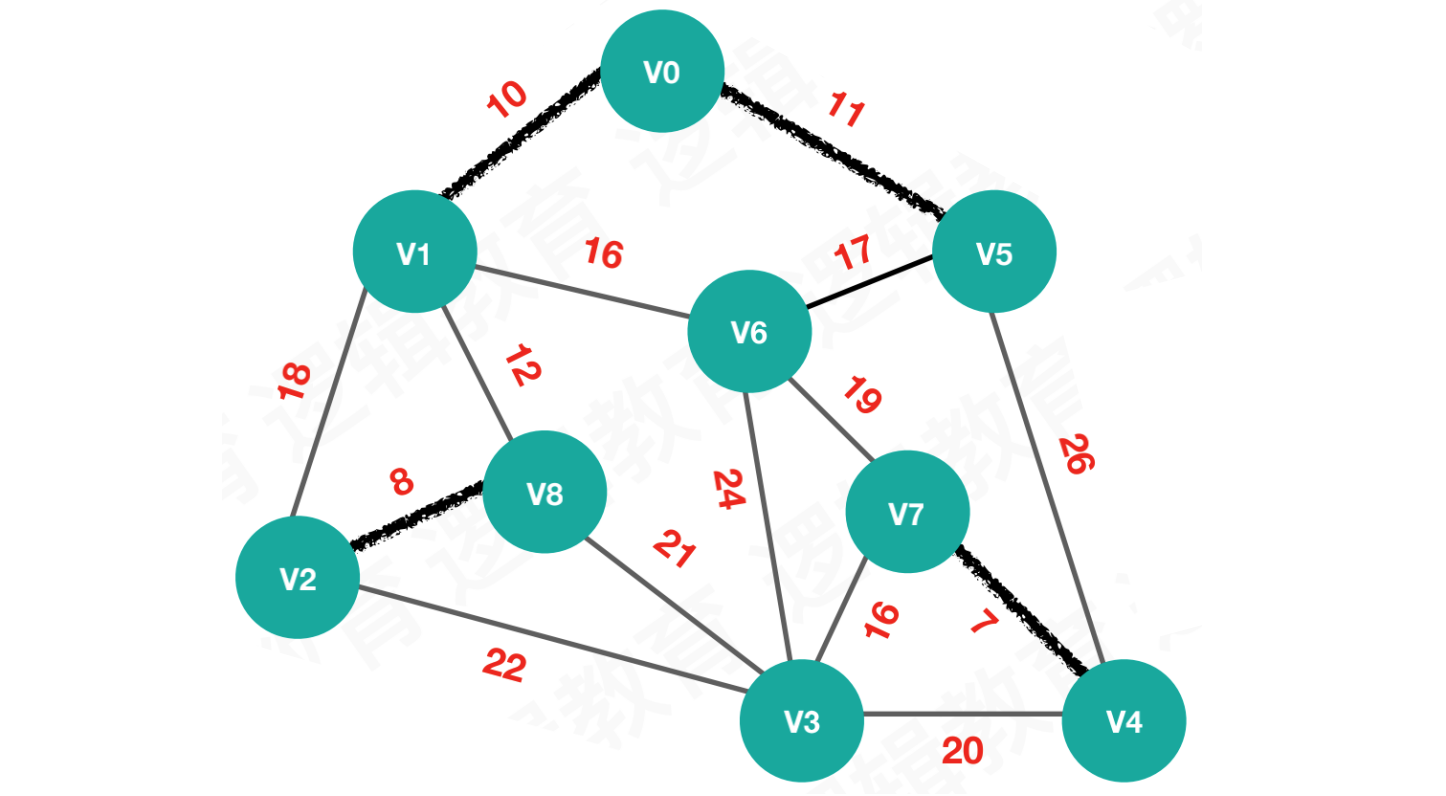
begin = 0,end = 5,weight = 11n = begin = 0,parent[0] == 1,则继续查找- 将结果
1作为索引值:parent[1] == 0,则n = 1
- 将结果
m = end = 5,parent[5] == 0,则m = 5
由于n != m,则parent[1] = 5
parent = [1, 5, 8, 0, 7, 0, 0, 0, 0]
【第五次执行】按照edges[4],连接V1和V8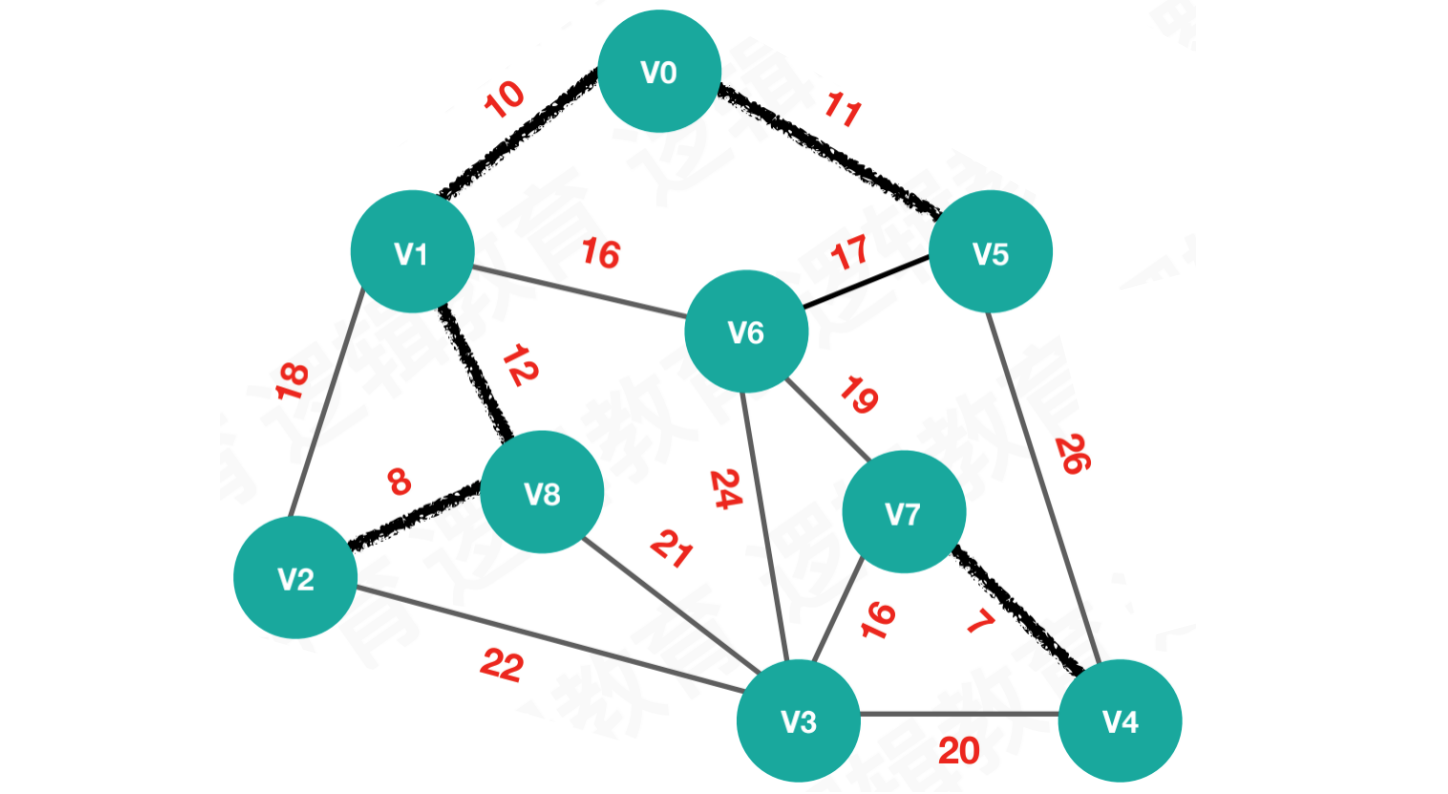
begin = 1,end = 8,weight = 12n = begin = 1,parent[1] == 5,则继续查找- 将结果
5作为索引值:parent[5] == 0,则n = 5
- 将结果
m = end = 8,parent[8] == 0,则m = 8
由于n != m,则parent[5] = 8
parent = [1, 5, 8, 0, 7, 8, 0, 0, 0]
【第六次执行】按照edges[5],连接V3和V7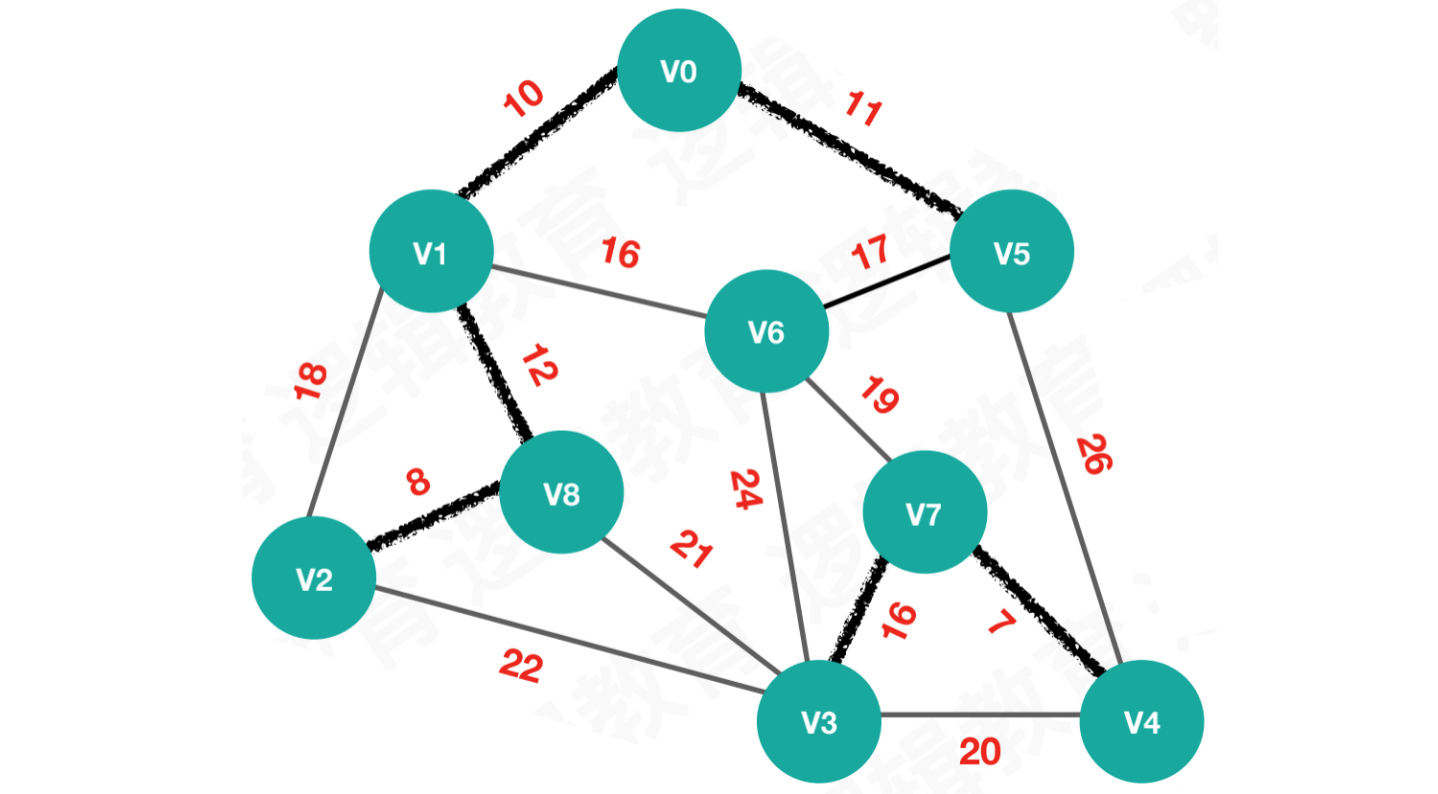
begin = 3,end = 7,weight = 16n = begin = 3,parent[3] == 0,则n = 3m = end = 7,parent[7] == 0,则m = 7
由于n != m,则parent[3] = 7
parent = [1, 5, 8, 7, 7, 8, 0, 0, 0]
【第七次执行】按照edges[6],连接V1和V6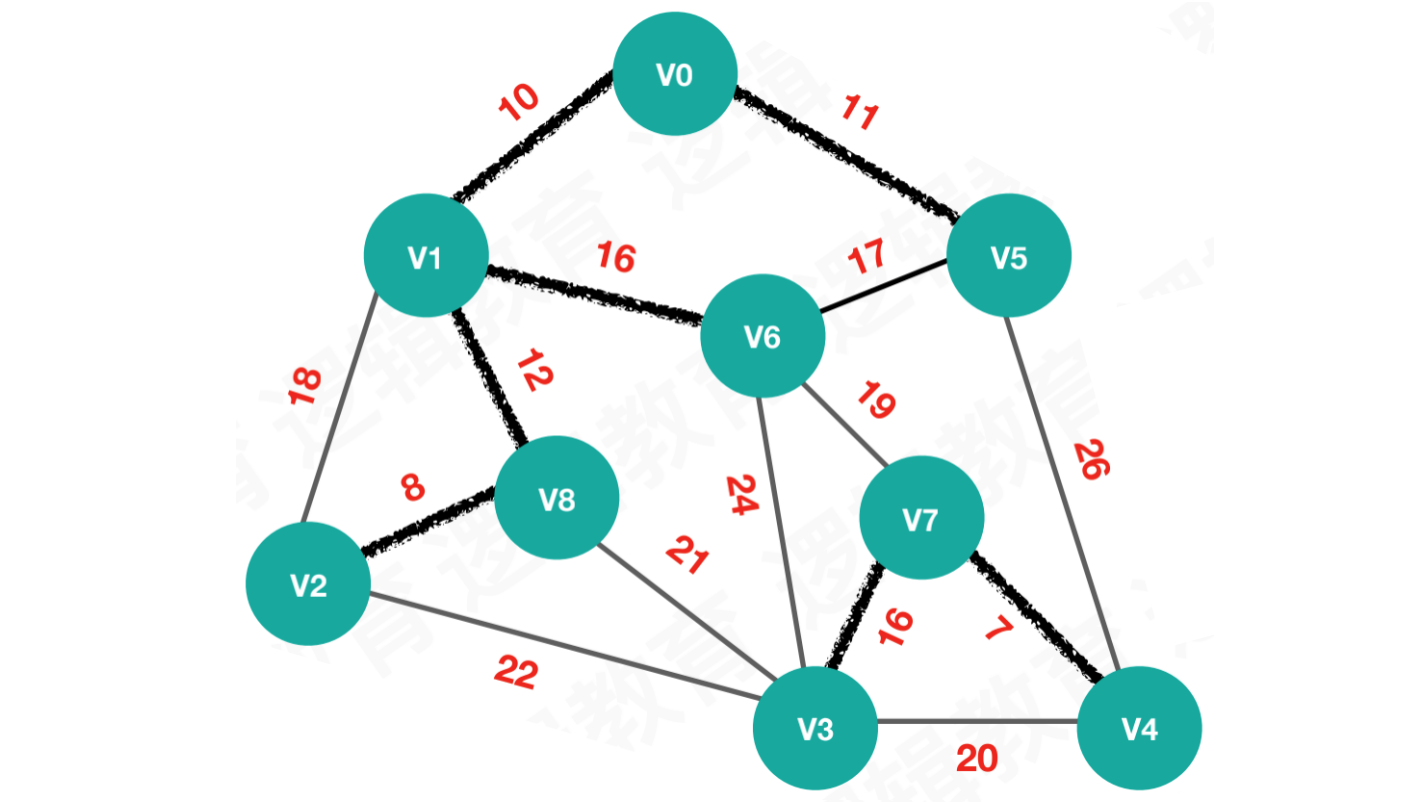
begin = 1,end = 6,weight = 16n = begin = 1,parent[1] == 5,则继续查找将结果
5作为索引值:parent[5] == 8,则继续查找将结果
8作为索引值:parent[8] == 0,则n = 8
m = end = 6,parent[6] == 0,则m = 6
由于n != m,则parent[7] = 6
parent = [1, 5, 8, 7, 7, 8, 0, 0, 6]
【环路情况】按照edges[7],连接V5和V6。或者按照edges[8],连接V1和V2,就会造成环路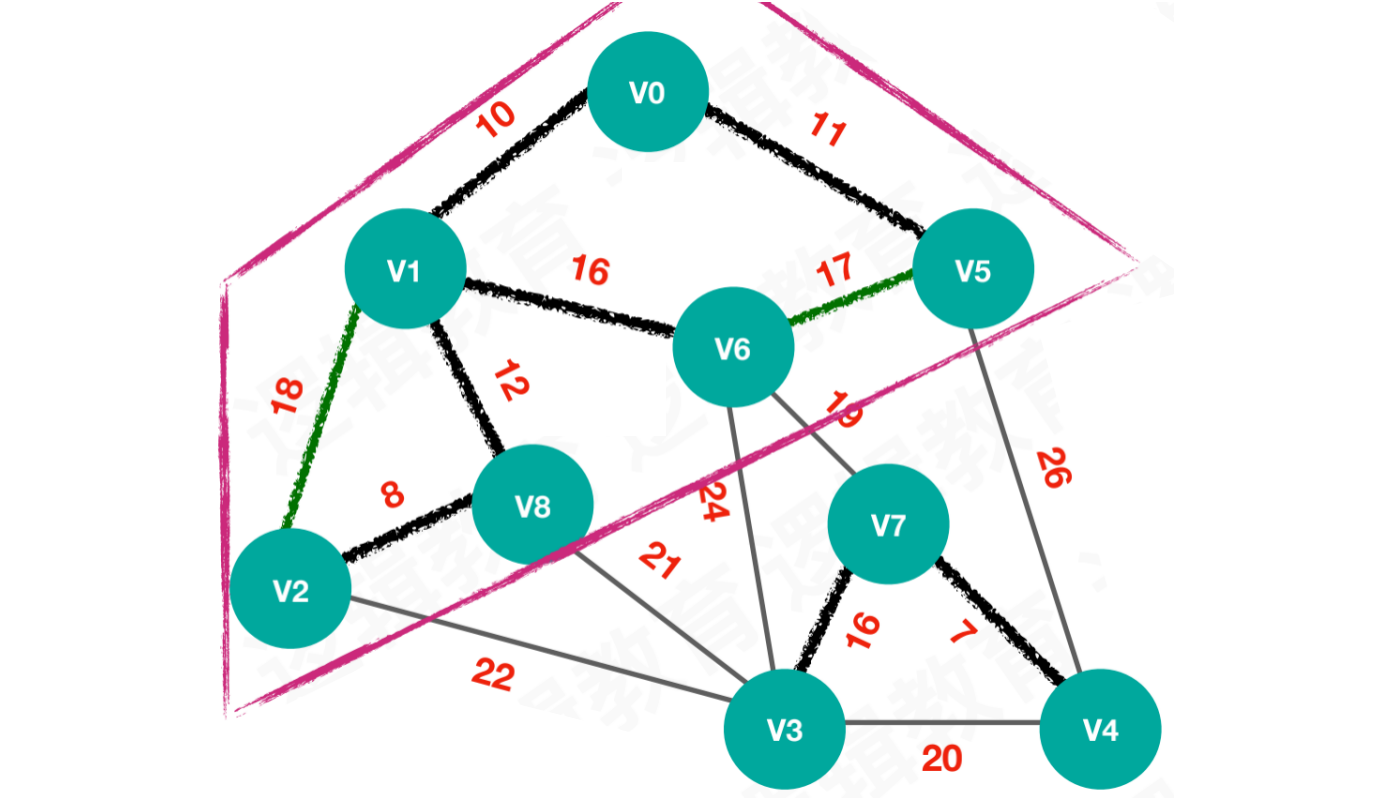
【第八次执行】按照edges[7],连接V5和V6
begin = 5,end = 6,weight = 17n = begin = 5,parent[5] == 8,则继续查找将结果
8作为索引值:parent[8] == 6,则继续查找将结果
6作为索引值:parent[6] == 0,则n = 6
m = end = 6,parent[6] == 0,则m = 6
由于n == m == 6,不能将它们加⼊最⼩⽣成树
【第九次执行】按照edges[8],连接V1和V2
begin = 1,end = 2,weight = 18n = begin = 1,parent[1] == 5,则继续查找将结果
5作为索引值:parent[5] == 8,则继续查找将结果
8作为索引值:parent[8] == 6,则继续查找将结果
6作为索引值:parent[6] == 0,则n = 6
m = end = 2,parent[2] == 8,则继续查找将结果
8作为索引值:parent[8] == 6,则继续查找将结果
6作为索引值:parent[6] == 0,则m = 6
由于n == m == 6,不能将它们加⼊最⼩⽣成树
【第十次执行】按照edges[9],连接V6和V7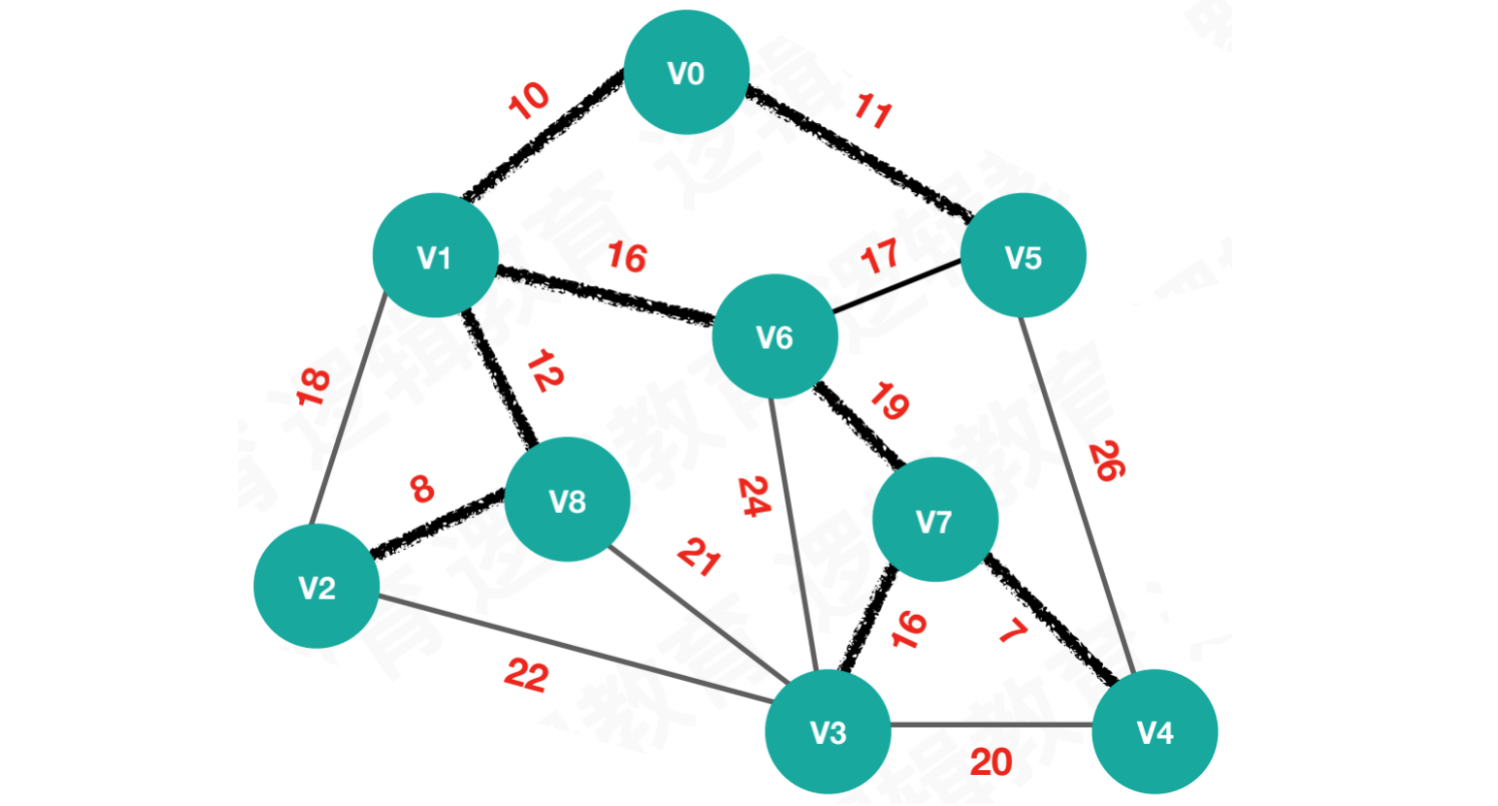
begin = 6,end = 7,weight = 19n = begin = 6,parent[6] == 0,则n = 6m = end = 7,parent[7] == 0,则m = 7
由于n != m,则parent[6] = 7
parent = [1, 5, 8, 7, 7, 8, 7, 0, 6]
【第十一次执行】按照edges[10],连接V3和V4
begin = 3,end = 4,weight = 20n = begin = 3,parent[3] == 7,则继续查找- 将结果
7作为索引值:parent[7] == 0,则n = 7
- 将结果
m = end = 4,parent[4] == 7,则继续查找- 将结果
7作为索引值:parent[7] == 0,则m = 7
- 将结果
由于n == m == 7,不能将它们加⼊最⼩⽣成树
【第十二次执行】按照edges[11],连接V3和V8
begin = 3,end = 8,weight = 21n = begin = 3,parent[3] == 7,则继续查找- 将结果
7作为索引值:parent[7] == 0,则n = 7
- 将结果
m = end = 8,parent[8] == 6,则继续查找将结果
6作为索引值:parent[6] == 7,则继续查找将结果
7作为索引值:parent[7] == 0,则m = 7
由于n == m == 7,不能将它们加⼊最⼩⽣成树
【第十三次执行】按照edges[12],连接V2和V3
begin = 2,end = 3,weight = 22n = begin = 2,parent[2] == 8,则继续查找将结果
8作为索引值:parent[8] == 6,则继续查找将结果
6作为索引值:parent[6] == 7,则继续查找将结果
7作为索引值:parent[7] == 0,则n = 7
m = end = 3,parent[3] == 7,则继续查找- 将结果
7作为索引值:parent[7] == 0,则m = 7
- 将结果
由于n == m == 7,不能将它们加⼊最⼩⽣成树
【第十四次执行】按照edges[13],连接V3和V6
begin = 3,end = 6,weight = 24n = begin = 3,parent[3] == 7,则继续查找- 将结果
7作为索引值:parent[7] == 0,则n = 7
- 将结果
m = end = 6,parent[6] == 7,则继续查找- 将结果
7作为索引值:parent[7] == 0,则m = 7
- 将结果
由于n == m == 7,不能将它们加⼊最⼩⽣成树
【第十五次执行】按照edges[14],连接V4和V5
begin = 4,end = 5,weight = 26n = begin = 4,parent[4] == 7,则继续查找- 将结果
7作为索引值:parent[7] == 0,则n = 7
- 将结果
m = end = 5,parent[5] == 8,则继续查找将结果
8作为索引值:parent[8] == 6,则继续查找将结果
6作为索引值:parent[6] == 7,则继续查找将结果
7作为索引值:parent[7] == 0,则m = 7
由于n == m == 7,不能将它们加⼊最⼩⽣成树
3.3 代码实现
延用“邻接矩阵存储”的案例代码,修改MGraphLinear类中代码
将邻接矩阵转为边表,增加排序方法
class MGraphLinear {
fileprivate class Edge {
var begin : Int;
var end : Int;
var weight : Int;
init(begin : Int, end : Int, weight : Int){
self.begin = begin;
self.end = end;
self.weight = weight;
}
}
fileprivate var edges : [Edge]?;
fileprivate var parent : [Int]?;
fileprivate func createEdges() {
self.edges = [Edge]();
for i in 0 ..< self.graph.numNodes {
for j in i + 1 ..< self.graph.numNodes {
let w = self.graph.arc![i][j];
if(w == Int.max){
continue;
}
let edge = Edge.init(begin: i, end: j, weight: w);
self.edges?.append(edge);
}
}
}
fileprivate func sortEdges() {
for i in 0 ..< self.edges!.count - 1 {
let edge1 = self.edges![i];
for j in i + 1 ..< self.edges!.count {
let edge2 = self.edges![j];
if(edge1.weight > edge2.weight){
let begin = edge1.begin;
let end = edge1.end;
let weight = edge1.weight;
edge1.begin = edge2.begin;
edge1.end = edge2.end;
edge1.weight = edge2.weight;
edge2.begin = begin;
edge2.end = end;
edge2.weight = weight;
}
}
}
}
}
增加边表的打印方法:
class MGraphLinear {
func traverseEdges() -> String {
var str : String = "";
for i in 0 ..< self.edges!.count {
let edge = self.edges![i];
str += "edges[\(i)] -> begin:\(edge.begin),end:\(edge.end),weight:\(edge.weight)\n";
}
return str;
}
}
实现Kruskal算法:
class MGraphLinear {
func miniSpanTree_kruskal() -> String {
var str = "";
var sum_text = "";
var sum_num = 0;
// 1、将邻接矩阵转为边表
createEdges();
// 按照权值进行升序
sortEdges();
// 打印边表信息
print(traverseEdges());
// 2、按顶点数,初始化parent数组,默认填充0
self.parent = [Int].init(repeating: 0, count: self.graph.numNodes);
// 记录加入最小生成树的顶点数所连接的边数
var count = 0;
// 3、遍历边表
for edge in self.edges! {
// 满足n - 1条边,证明已经加满,退出循环
if(count == self.parent!.count - 1){
break;
}
// 根据begin和end,寻找n和m
let n = find(index: edge.begin);
let m = find(index: edge.end);
// n和m相等,表示会产生闭环,相关顶点不能加入最小生成树
if(n == m){
continue;
}
// 不相等,表示当前为有效路径,将m存储到parent[n]中标记
self.parent![n] = m;
// 加入最小生成树的顶点数+1
count += 1;
// 记录最小生成树路径,累加权值的总和
str += "\(self.graph.vexs![edge.begin]) -> \(self.graph.vexs![edge.end]) = \(edge.weight)\n";
sum_text += "\(edge.weight) + ";
sum_num += edge.weight;
}
sum_text = "\(sum_text.prefix(sum_text.count - 2)) = \(sum_num)";
print("Sum:\(sum_text)\n");
return str;
}
fileprivate func find(index : Int) -> Int {
var n = index;
while(self.parent![n] != 0){
n = self.parent![n];
}
return n;
}
}
打印Kruskal算法的结果:
let nodes = ["V0", "V1", "V2", "V3", "V4", "V5", "V6", "V7", "V8"];
let edges = [[0, 1 ,10], [0, 5, 11],
[1, 2, 18], [1, 6, 16], [1, 8, 12],
[2, 3, 22], [2, 8, 8],
[3, 4, 20], [3, 6, 24], [3, 7, 16], [3, 8, 21],
[4, 5, 26], [4, 7, 7],
[5, 6, 17],
[6, 7, 19]];
let isUndirected = true;
let isNet = true;
let graphLinear = MGraphLinear();
graphLinear.create(nodes: nodes, edges: edges, isUndirected: isUndirected, isNet: isNet);
print("\(graphLinear.miniSpanTree_kruskal())");
-------------------------
//输出以下内容:
edges[0] -> begin:4,end:7,weight:7
edges[1] -> begin:2,end:8,weight:8
edges[2] -> begin:0,end:1,weight:10
edges[3] -> begin:0,end:5,weight:11
edges[4] -> begin:1,end:8,weight:12
edges[5] -> begin:3,end:7,weight:16
edges[6] -> begin:1,end:6,weight:16
edges[7] -> begin:5,end:6,weight:17
edges[8] -> begin:1,end:2,weight:18
edges[9] -> begin:6,end:7,weight:19
edges[10] -> begin:3,end:4,weight:20
edges[11] -> begin:3,end:8,weight:21
edges[12] -> begin:2,end:3,weight:22
edges[13] -> begin:3,end:6,weight:24
edges[14] -> begin:4,end:5,weight:26
Sum:7 + 8 + 10 + 11 + 12 + 16 + 16 + 19 = 99
V4 -> V7 = 7
V2 -> V8 = 8
V0 -> V1 = 10
V0 -> V5 = 11
V1 -> V8 = 12
V3 -> V7 = 16
V1 -> V6 = 16
V6 -> V7 = 19
总结
连通图的⽣成树:
定义:所谓⼀个连通图的⽣成树,它不是树,而是⼀个极⼩的连通⼦图。它含有图中全部的
N个顶点,但只⾜以构成⼀颗树的N - 1条边满⾜以下三个条件则为连通图的⽣成树:
图是连通图
图中包含
N个顶点图中边的数量等于
N - 1条边
最小生成树:
- 定义:把构成连通⽹的最⼩代价的⽣成树称为最⼩⽣成树
普⾥姆(Prim)算法:
特点:从任意一个顶点开始,每次选择一个与当前顶点集最近的一个顶点,并将两顶点之间的边加入到树中。
Prim算法在找当前最近顶点时使用到了贪心算法- 贪心算法:在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,算法得到的是在某种意义上的局部最优解
思路:
定义两个一维数组,
adjvex⽤来保存相关顶点下标,lowcost保存顶点之间的权值初始化两个数组,从
v0开始寻找最⼩⽣成树。默认v0是最⼩⽣成树上第⼀个顶点循环
lowcost数组,根据权值找到顶点k更新
lowcost数组循环所有顶点,找到与顶点k有关系的顶点,并更新
lowcost数组与adjvex数组。符合以下条件则更新:与
顶点k之间有连接当前
结点j没有加⼊过最⼩⽣成树顶点k与当前顶点j之间的权值,⼩于顶点j与其他顶点k之前的权值,则更新。简单说:就是要⽐较之前存储的值要⼩,则更新
克鲁斯卡尔(Kruskal)算法:
特点:利用有限的连接信息,推断顶点之间是否会产生闭环
思路:
将邻接矩阵转化成边表数组
对边表数组根据权值按照从⼩到⼤的顺序排序
遍历所有的边,通过
parent数组找到边的连接信息,避免闭环问题如果不存在闭环问题,则加⼊到最⼩⽣成树中,并且修改
parent数组

