数据结构算法--015：图的应用之关键路径

1. 概述

在⼀个表示⼯程的带权有向图中，⽤顶点表示事件，⽤有向边表示活动，⽤边上的权值表示活动的持续时间，这种有向图的边表表示活动的⽹，我们称之为AOE⽹（Activity On Edge Network）

• 和AOV网的区别在于权值，AOV网的边上没有权值，它在执行任务时只考虑先后顺序

• 符合AOE网的前提条件是，必须也要符合AOV网。在有权值的同时，任务之间也要有先后顺序

1.1 名词解释

• 由于⼀个⼯程，总有⼀个开始和⼀个结束，所以正常情况下，AOE⽹只有⼀个源点和⼀个汇点

  • 没有⼊边的顶点称为始点或源点，即：入度为0

  • 没有出边的顶点称为终点或汇点，即：出度为0

• 路径上各个活动所持续的时间之和称为路径⻓度

• 从源点到汇点具有最⼤的路径叫关键路径

• 在关键路径上的活动叫关键活动

例如：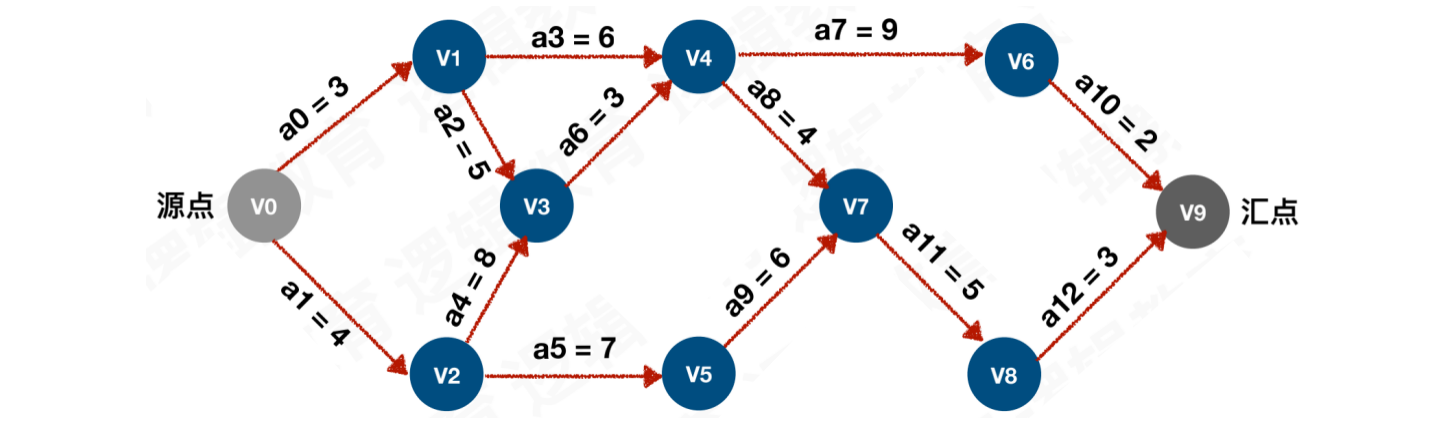

• 顶点V0入度为0，即：V0为源点

• 顶点V9出度为0，即：V9为汇点

1.2 关键路径

假设：造⼀辆汽⻋，我们需要先造各种各样的零件、部件，最终才能完成汽⻋的组装

如图：这些零部件基本都是在流⽔线同时⽣产的。假如造⼀个轮⼦，需要0.5天的时间，造⼀个发动机需要3天时间，造⼀个⻋底盘需要2天时间，其他零部件需要2天时间，全部零部件集中到⼀处需要0.5天，组装成汽⻋需要2天时间，请问⼀个汽⻋⼚造⼀台汽⻋，最短需要多⻓时间？

合理的做法：我们应该并行生产所需的零部件，在造发动机的3天时间中，可以生产6个轮⼦，并且同时生产底盘和其他零部件。当生成结束后，花费0.5天将零部件集中，再花费2天组装成汽⻋，最短需要5.5天

使用AOE⽹图显示：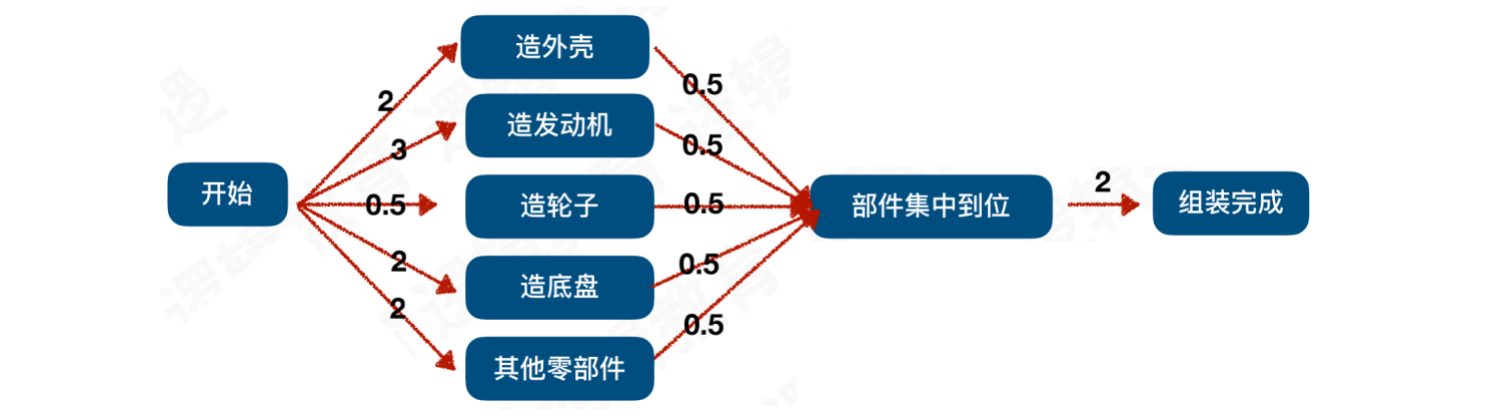

• 此图的关键路径，找到能够覆盖所有活动的最大路径。即：造发动机 → 部件集中 →组装

求解关键路径的目的：如果我们要对工厂制造汽车的工期进行优化，我们需要优化造发动机的时间，只有将耗时最长的任务优化，才能提升整体工期

1.3 核⼼参数

• 事件最早发⽣的时间etv（earliest time of vertex）：即顶点Vk的最早发⽣时间

• 事件最晚发⽣时间ltv（latest time of vertex）：即顶点Vk的最晚发⽣时间，也就是每个顶点对应的事件最晚需要开始的时间，超出此时间将会延误整个⼯期

• 活动的最早开⼯时间ete（earliest time of edge）：即弧Ak的最早发⽣时间

• 活动的最晚开⼯时间lte（latest time of edge）：即弧Ak的最晚发⽣时间，也就是不推迟⼯期的最晚开⼯时间

2. 求解etv

事件最早发⽣的时间etv（earliest time of vertex）：即顶点Vk的最早发⽣时间

2.1 算法解析

以此图为例：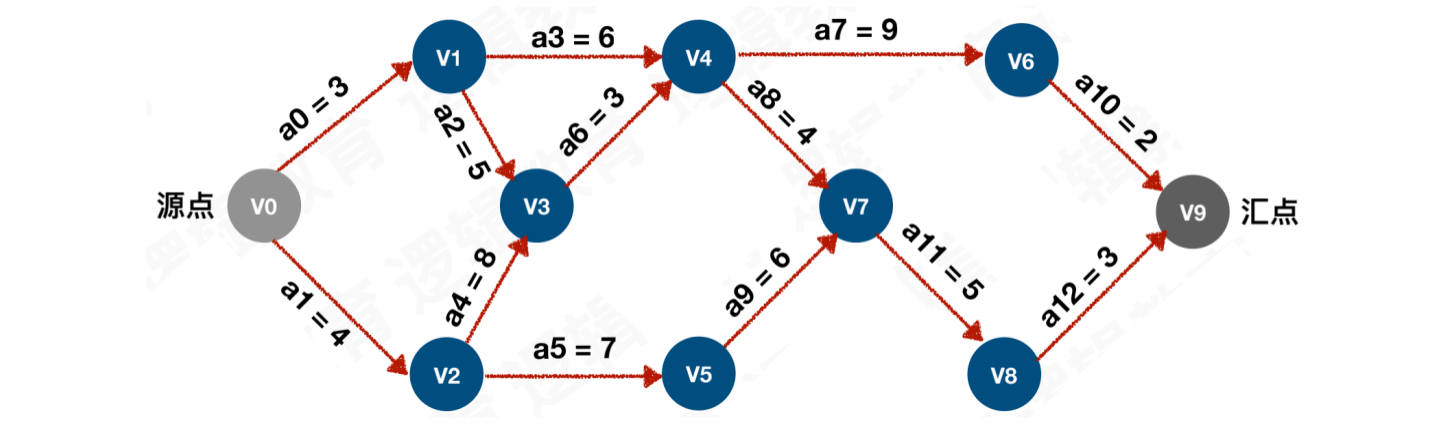

• 求解事件的最早发⽣时间etv的过程，就是从头到尾去找拓扑序列的过程。所以在求解关键路径之前，我们需要调⽤⼀次拓扑排序的序列，同时计算etv和拓扑序列列表

求解顶点V3的最早发生时间：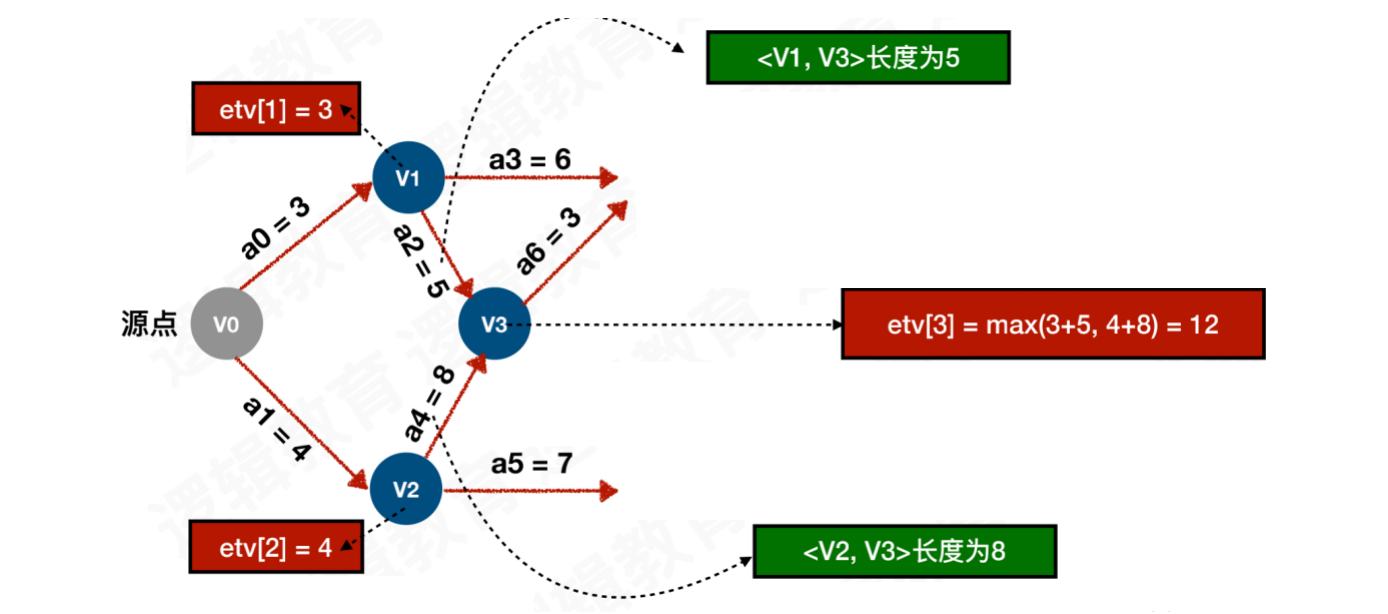

• V3⼊边的顶点分别为V1和V2，其中V1 → V3 = 5，V2 → V3 = 8。求解V3的耗时，还需要加上V1和V2的事件的耗时

  • V0 → V1 → V3 = 3 + 5 = 8

  • V0 → V2 → V3 = 4 + 8 = 12

• 找到事件的耗时，例如要完成V3，需要V1、V2两个条件同时达成。那么V1需要8⼩时，而V2需要12⼩时，此时完成V3必须等待12⼩时。所以寻找事件的耗时，需要选择耗时更⻓的为最早发⽣时间

公式推演：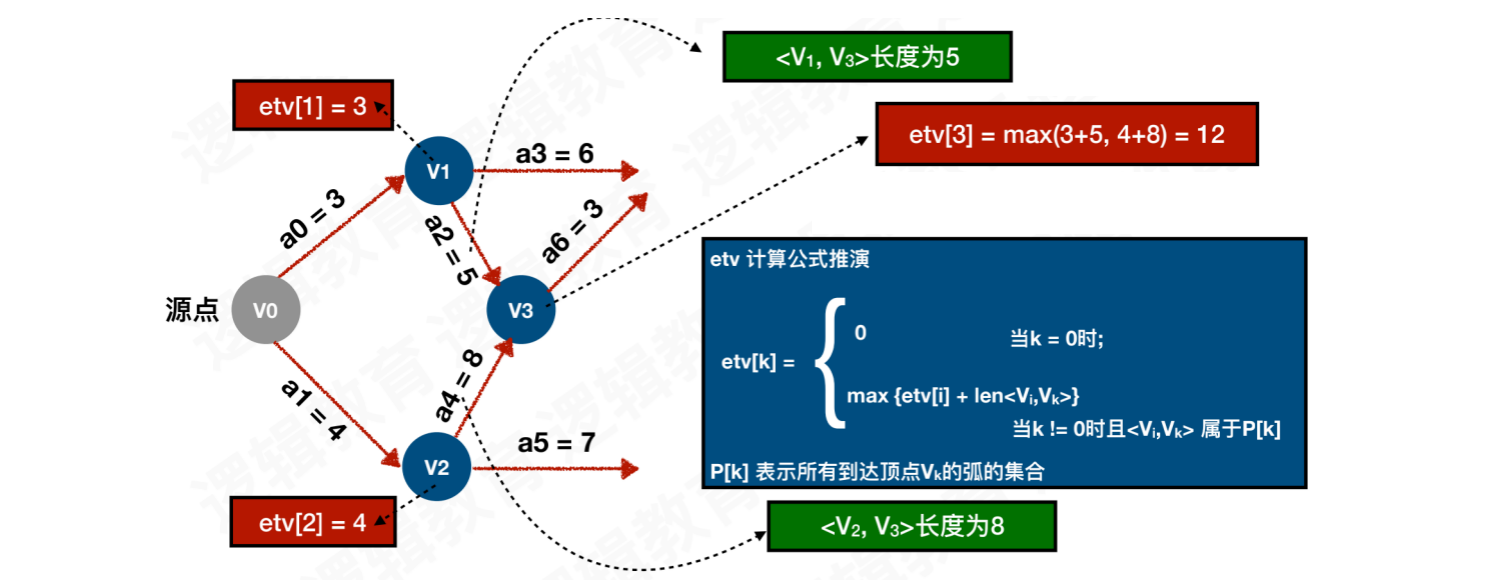

• 当k == 0时，顶点Vk的入度为0，故此Vk的etv也为0

• 当入度 > 0时，需要使用入边的顶点Vi所需的etv值，加上Vi → Vk的权值。如果有多条到达Vk的弧，选择最大的etv结果

2.2 代码实现

创建AoeGraphLinked类，定义数据结构：

class AoeGraphLinked {
    fileprivate class Node {
        var adj_vex_index : Int?;
        var weight : Int?;
        var data : String?;
        var next : Node?;
    }
    fileprivate class VNode {
        var inDegree : Int;
        var data : String?;
        var firstEdge : Node?;
        init(){
            self.inDegree = 0;
        }
    }
    fileprivate class Graph {
        var adjList : [VNode]?;
        var arc_num : Int;
        var node_num : Int;
        init(){
            self.arc_num = 0;
            self.node_num = 0;
        }
    }
    fileprivate var graph : Graph;
    init(){
        self.graph = Graph();
    }
}

实现创建和打印方法：

class AoeGraphLinked {

    func create(nodes : [String], arcs : [[Int]]) {

        self.graph.arc_num = arcs.count;
        self.graph.node_num = nodes.count;
        self.graph.adjList = [VNode]();

        for data in nodes {
            let vNode = VNode();
            vNode.data = data;
            self.graph.adjList?.append(vNode);
        }

        for arc in arcs {

            let i = arc[0];
            let j = arc[1];
            let w = arc[2];

            let node = Node();
            node.adj_vex_index = j;
            node.weight = w;
            node.data = self.graph.adjList![j].data;
            self.graph.adjList![j].inDegree += 1;

            let vNode = self.graph.adjList![i];
            node.next = vNode.firstEdge;
            vNode.firstEdge = node;
        }
    }

    func traverse() -> String {

        var str : String = "";

        for vNode in self.graph.adjList! {

            var node = vNode.firstEdge;

            str += "入度：\(vNode.inDegree)，\(vNode.data!)"

            while(node != nil){
                str += " -> \(node!.data!)【权值：\(node!.weight!)】";
                node = node?.next;
            }

            str += "\n";
        }

        return str;
    }
}

Aoe网图是在Aov网图的基础上增加权值，所以在拓扑排序的同时时，可以进行etv的求解：

class AoeGraphLinked {

    // 存储入度为0的顶点
    fileprivate var stack : LinearStack<Int>?;
    // 存储拓扑排序的结果
    fileprivate var topResult_stack : LinearStack<Int>?;
    // 存储etv的结果
    fileprivate var etv : [Int]?;

    // 完成拓扑排序，同时求解etv
    func topologicalSort() -> String {

        var str : String = "";

        self.stack = LinearStack<Int>.init(capacity: self.graph.adjList!.count);
        self.topResult_stack = LinearStack<Int>.init(capacity: self.graph.adjList!.count);
        self.etv = [Int].init(repeating: 0, count: self.graph.adjList!.count);

        // 1、将入度为0的顶点对应的索引值入栈
        for i in 0 ..< self.graph.adjList!.count {

            let vNode = self.graph.adjList![i];

            if(vNode.inDegree > 0){
                continue;
            }

            self.stack!.push(element: i);
        }

        var count = 0;

        // 2、遍历stack
        while(!self.stack!.isEmpty()) {

            // 将数据依次出栈，并且count++
            let i = self.stack!.pop()!;
            count += 1;

            // 通过索引在顶点表中获取顶点
            let vNode = self.graph.adjList![i];
            str += "\(vNode.data!) -> ";

            // 存储拓扑排序的结果
            self.topResult_stack?.push(element: i);

            // 获取顶点指向边表中的头结点
            var node = vNode.firstEdge;

            // 遍历边表中的顶点
            while(node != nil){

                let k = node!.adj_vex_index!;

                // 将顶点的入度-1
                let vNode = self.graph.adjList![k];
                vNode.inDegree -= 1;

                // 如果-1后顶点的入度为0，将其索引值入栈
                if(vNode.inDegree == 0){
                    self.stack!.push(element: k);
                }

                // 3、求解etv，存储etv的结果
                if(self.etv![i] + node!.weight! > self.etv![k]){
                    self.etv![k] = self.etv![i] + node!.weight!;
                }

                node = node?.next;
            }
        }

        // 4、判断输出的顶点是否为正确的拓扑排序
        if(count < self.graph.node_num){
            self.topResult_stack?.clear();
            str = "执行失败，图结构非AOV网图";
        }

        return str;
    }
}

3. 求解ltv

事件最晚发⽣时间ltv（latest time of vertex）：即顶点Vk的最晚发⽣时间，也就是每个顶点对应的事件最晚需要开始的时间，超出此时间将会延误整个⼯期

3.1 算法解析

【初始化】定义ltv数组，用于存储事件最晚发⽣时间。默认使用etv中最后事件的时间填充ltv数组，然后按照拓扑排序的结果遍历顶点，并依次计算各顶点对应的ltv值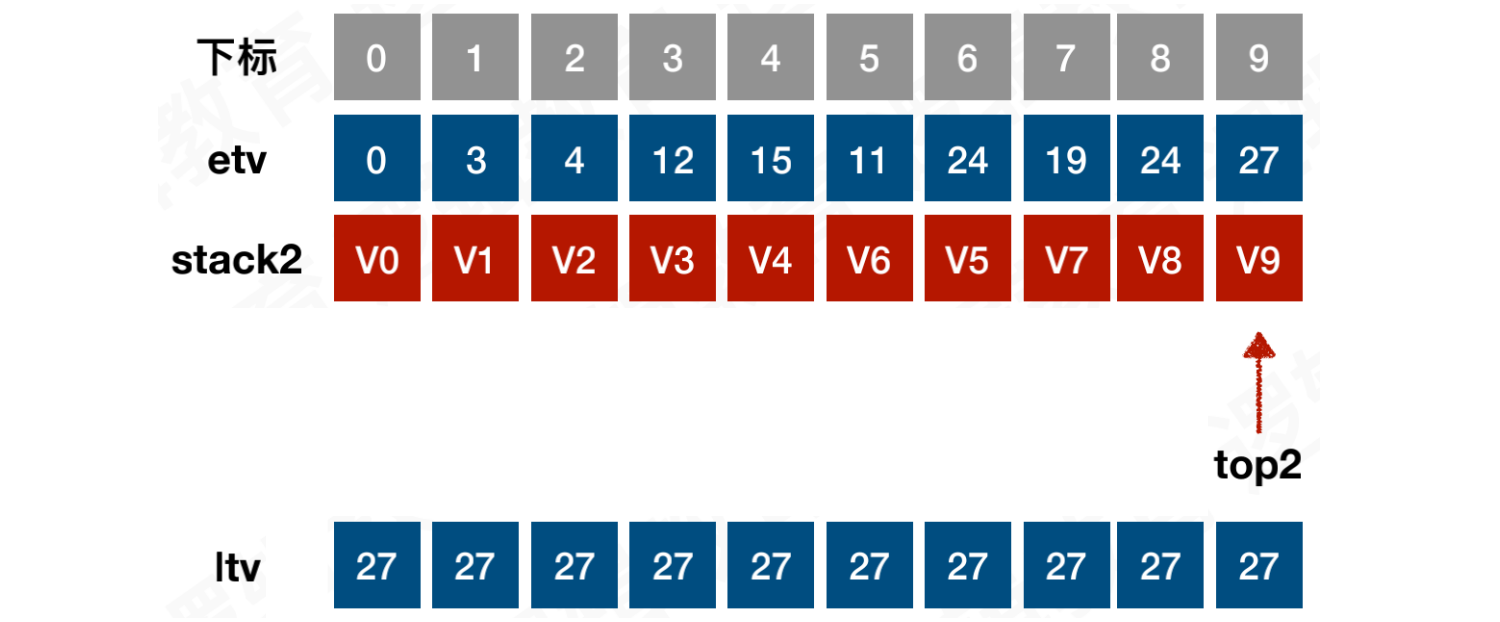

【第一次执行】遍历stack2栈，栈顶gettop = 9出栈

由于V9没有弧表，则没有相关的ltv更新

ltv = [27, 27, 27, 27, 27, 27, 27, 27, 27, 27]

【第二次执行】遍历stack2栈，栈顶gettop = 8出栈

V8连接V9，权重为3，更新ltv[8] = ltv[9] - node.weight = 27 - 3 = 24

ltv = [27, 27, 27, 27, 27, 27, 27, 27, 24, 27]

【第三次执行】遍历stack2栈，栈顶gettop = 7出栈

V7连接V8，权重为5，更新ltv[7] = ltv[8] - node.weight = 24 - 5 = 19

ltv = [27, 27, 27, 27, 27, 27, 27, 19, 24, 27]

【第四次执行】遍历stack2栈，栈顶gettop = 5出栈

V5连接V7，权重为6，更新ltv[5] = ltv[7] - node.weight = 19 - 6 = 13

ltv = [27, 27, 27, 27, 27, 13, 27, 19, 24, 27]

【第五次执行】遍历stack2栈，栈顶gettop = 6出栈

V6连接V9，权重为2，更新ltv[6] = ltv[9] - node.weight = 27 - 2 = 25

ltv = [27, 27, 27, 27, 27, 13, 25, 19, 24, 27]

【第六次执行】遍历stack2栈，栈顶gettop = 4出栈

V4分别连接V6和V7，权重为9和4。分别计算出V4 → V6与V4 → V7的值，选择其中最小的ltv

• V4 → V6 = ltv[6] - node.weight = 25 - 9 = 16

• V4 → V7 = ltv[7] - node.weight = 19 - 4 = 15

更新ltv[4] = min(19 - 4, 25 - 9) = 15

ltv = [27, 27, 27, 27, 15, 13, 25, 19, 24, 27]

【第七次执行】遍历stack2栈，栈顶gettop = 3出栈

V3连接V4，权重为3，更新ltv[3] = ltv[4] - node.weight = 15 - 3 = 12

ltv = [27, 27, 27, 12, 15, 13, 25, 19, 24, 27]

【第八次执行】遍历stack2栈，栈顶gettop = 2出栈

V2分别连接V3和V5，权重为8和7。分别计算出V2 → V3与V2 → V5的值，选择其中最小的ltv

• V2 → V3 = ltv[3] - node.weight = 12 - 8 = 4

• V2 → V5 = ltv[5] - node.weight = 13 - 7 = 4

更新ltv[2] = min(12 - 8, 13 - 7) = 4

ltv = [27, 27, 4, 12, 15, 13, 25, 19, 24, 27]

【第九次执行】遍历stack2栈，栈顶gettop = 1出栈

V1分别连接V3和V4，权重为5和6。分别计算出V1 → V3与V1 → V4的值，选择其中最小的ltv

• V1 → V3 = ltv[3] - node.weight = 12 - 5 = 7

• V1 → V4 = ltv[4] - node.weight = 15 - 6 = 9

更新ltv[1] = min(12 - 5, 15 - 6) = 7

ltv = [27, 7, 4, 12, 15, 13, 25, 19, 24, 27]

【第十次执行】遍历stack2栈，栈顶gettop = 0出栈

V0分别连接V1和V2，权重为3和4。分别计算出V0 → V1与V0 → V2的值，选择其中最小的ltv

• V0 → V1 = ltv[1] - node.weight = 7 - 3 = 4

• V0 → V2 = ltv[1] - node.weight = 4 - 4 = 0

更新ltv[0] = min(7 - 3, 4 - 4) = 0

ltv = [0, 7, 4, 12, 15, 13, 25, 19, 24, 27]

公式推演：

• 当k == n - 1时，顶点Vk的出度为0，故此Vk的ltv等于etv[k]

• 当出度 > 0时，使用出边的顶点Vi所需的ltv值，减去Vi → Vk的权值。如果有多条到达Vk的弧，选择最小的ltv结果

3.2 代码实现

实现求解事件最晚开始时间的方法：

class AoeGraphLinked {

    // 存储ltv的结果
    fileprivate var ltv : [Int]?;

    // 求解ltv
    fileprivate func solveLtv(){

        // 默认使用etv中最后事件的时间填充
        self.ltv = [Int].init(repeating: etv!.last!, count: self.graph.node_num);

        // 按照拓扑排序的结果遍历顶点
        while(!self.topResult_stack!.isEmpty()){

            let k = self.topResult_stack!.pop()!;

            // 当k == n - 1时，Vk的ltv等于etv[k]
            if(k == self.graph.node_num - 1){
                continue;
            }

            // 获得顶点
            let vNode = self.graph.adjList![k];
            // 获得边表中头结点
            var node = vNode.firstEdge;

            // 遍历边表
            while(node != nil){

                let i = node!.adj_vex_index!;
                let i_ltv = self.ltv![i];
                // 使用出边的顶点Vi所需的ltv值，减去Vi → Vk的权值
                let tmp_ltv = i_ltv - node!.weight!;

                // 如果有多条到达Vk的弧，选择最小的ltv结果
                if(tmp_ltv < self.ltv![k]){
                    self.ltv![k] = tmp_ltv;
                }

                node = node?.next;
            }
        }
    }
}

4. 求解关键路径

拓扑序列：指的是事件在执⾏的顺序

关键活动：指的是从开始到结束具有最⼤⻓度的路径叫关键路径，⽽关键路径上的的活动叫做关键活动

• 示例中，V2是关键活动，因为V2的所需时间大于V1，所以当V2完成时，V1已经完成

• V3、V4也是关键活动，因为V2 → V3 → V4 → V7所需时间大于V2 → V5 → V7，所以当V3、V4完成时，V5已经完成。

• 同样V4 → V7 → V8 → V9和V4 → V6 → V9所需时间相同，当V7、V8完成时，V6也能同时完成

如图：

• ete表示活动Vk → Vj的最早开⼯时间，是针对这条弧来说的。⽽这条弧的弧尾顶点Vk的事件发⽣了，它才可以发⽣。因此ete = etv[k]

• lte表示活动Vk → Vj的最晚开⼯时间，但此活动再晚也不能等Vj事件发⽣才开始，⽽是必须在Vj事件之前发⽣。所以lte = ltv[j] - len<Vk, Vj>

• 例如，我们需要2⼩时完成作业，并且必须在23点睡觉。所以我们不能在23点才开始做作业，⽽是必须提前2⼩时在21点开始，才能按计划在23点睡觉

• 所以, 如果判断ete与lte是否相等，相等就意味着活动之间没有任何空闲时间，则它是关键活动，否则不是

4.1 算法解析

当我们计算出所有顶点的etv和ltv后，开始所有顶点的遍历

【第一次执行】当k == 0时，ete = etv[0] = 0。顶点V0连接V1和V2，分别计算它们的lte值：

• V0 → V1权值为3，ltv[1] = 7，lte = 7 - 3 = 4，由于0 != 4，所以V0 → V1不是关键路径

• V0 → V2权值为4，ltv[2] = 4，lte = 4 - 4 = 0，由于0 == 0，所以V0 → V2是关键路径

【第二次执行】当k == 1时，ete = etv[1] = 3。顶点V1连接V3和V4，分别计算它们的ltv：

• V1 → V3权值为5，ltv[3] = 12，lte = 12 - 5 = 7，由于3 != 7，所以V1 → V3不是关键路径

• V1 → V4权值为6，ltv[4] = 15，lte = 15 - 6 = 9，由于3 != 9，所以V1 → V4不是关键路径

【第三次执行】当k == 2时，ete = etv[2] = 4。顶点V2连接V3和V5，分别计算它们的ltv：

• V2 → V3权值为8，ltv[3] = 12，lte = 12 - 8 = 4，由于4 == 4，所以V2 → V3是关键路径

• V2 → V5权值为7，ltv[5] = 15，lte = 15 - 7 = 8，由于8 != 4，所以V2 → V5不是关键路径

【第四次执行】当k == 3时，ete = etv[3] = 12。顶点V3连接V4，分别计算它们的ltv：

• V3 → V4权值为3，ltv[4] = 15，lte = 15 - 3 = 12，由于12 == 12，所以V3 → V4是关键路径

【第五次执行】当k == 4时，ete = etv[4] = 15。顶点V4连接V6和V7，分别计算它们的ltv：

• V4 → V6权值为9，ltv[6] = 25，lte = 25 - 9 = 16，由于16 != 15，所以V4 → V6不是关键路径

• V4 → V7权值为4，ltv[7] = 19，lte = 19 - 4 = 15，由于15 == 15，所以V4 → V7是关键路径

【第六次执行】当k == 5时，ete = etv[5] = 11。顶点V5连接V7，分别计算它们的ltv：

• V5 → V7权值为6，ltv[7] = 19，lte = 19 - 6 = 13，由于13 != 11，所以V5 → V7不是关键路径

【第七次执行】当k == 6时，ete = etv[6] = 24。顶点V6连接V9，分别计算它们的ltv：

• V6 → V9权值为2，ltv[9] = 27，lte = 27 - 2 = 25，由于25 != 24，所以V6 → V9不是关键路径

【第八次执行】当k == 7时，ete = etv[7] = 19。顶点V7连接V8，分别计算它们的ltv：

• V7 → V8权值为5，ltv[8] = 24，lte = 24 - 5 = 19，由于19 == 19，所以V7 → V8是关键路径

【第九次执行】当k == 8时，ete = etv[8] = 24。顶点V8连接V9，分别计算它们的ltv：

• V8 → V9权值为3，ltv[9] = 27，lte = 27 - 3 = 24，由于24 == 24，所以V8 → V9是关键路径

【第十次执行】当k == 9时，ete = etv[9] = 27。V9为汇点，跳过该循环

4.2 代码实现

实现求解关键路径的方法：

class AoeGraphLinked {

    // 求解关键路径
    func criticalPath() -> String {

        var str : String = "";

        // 1、完成拓扑排序，同时计算etv
        print("拓扑排序：\(topologicalSort())\n");
        // 2、计算ltv
        solveLtv();

        print("etv：\(self.etv!)");
        print("ltv：\(self.ltv!)\n");

        // 3、遍历所以顶点
        for k in 0 ..< self.graph.node_num {

            // 获取ete
            let ete = self.etv![k];
            // 获取顶点
            let vNode = self.graph.adjList![k];
            // 获取边表的头结点
            var node = vNode.firstEdge;

            // 遍历边表结点
            while(node != nil) {

                let j = node!.adj_vex_index!;
                // 获取ltv
                let ltv = self.ltv![j];
                // 计算lte
                let lte = ltv - node!.weight!;

                // 相等，表示Vk → Vj是关键路径
                if(ete == lte){

                    if(str.isEmpty){
                        str += "\(vNode.data!)";
                    }

                    str += " -> \(node!.data!)";
                }

                // 遍历下一个结点
                node = node?.next;
            }
        }

        return str;
    }
}

按照示例中的AOE网图逻辑，使用代码创建邻接表，并打印关键路径：

let nodes = ["V0", "V1", "V2", "V3", "V4", "V5", "V6", "V7", "V8", "V9"];
let arcs = [[0, 1, 3], [0, 2, 4],
            [1, 3, 5], [1, 4, 6],
            [2, 3, 8], [2, 5, 7],
            [3, 4, 3],
            [4, 6, 9], [4, 7, 4],
            [5, 7, 6],
            [6, 9, 2],
            [7, 8, 5],
            [8, 9, 3]];

let aoeGraphLinked = AoeGraphLinked();
aoeGraphLinked.create(nodes: nodes, arcs: arcs);
print(aoeGraphLinked.traverse());
print("关键路径：\(aoeGraphLinked.criticalPath())");

-------------------------
//输出以下内容：
入度：0，V0 -> V2【权值：4】 -> V1【权值：3】
入度：1，V1 -> V4【权值：6】 -> V3【权值：5】
入度：1，V2 -> V5【权值：7】 -> V3【权值：8】
入度：2，V3 -> V4【权值：3】
入度：2，V4 -> V7【权值：4】 -> V6【权值：9】
入度：1，V5 -> V7【权值：6】
入度：1，V6 -> V9【权值：2】
入度：2，V7 -> V8【权值：5】
入度：1，V8 -> V9【权值：3】
入度：2，V9

拓扑排序：V0 -> V1 -> V2 -> V3 -> V4 -> V6 -> V5 -> V7 -> V8 -> V9 -> 

etv：[0, 3, 4, 12, 15, 11, 24, 19, 24, 27]
ltv：[0, 7, 4, 12, 15, 13, 25, 19, 24, 27]

关键路径：V0 -> V2 -> V3 -> V4 -> V7 -> V8 -> V9

4.3 时间复杂度

顶点表长度为n，边表长度为e

• 拓扑排序的时间复杂度：O(n + e)

• 初始化ltv时间复杂度：O(n)

• 计算ltv的时间复杂度：O(n + e)

• 计算ete、lte时间复杂度：O(n + e)

• 所以最终求解关键路径的时间复杂度为：O(n + e)

总结

概述：

在⼀个表示⼯程的带权有向图中，⽤顶点表示事件，⽤有向边表示活动，⽤边上的权值表示活动的持续时间，这种有向图的边表表示活动的⽹，我们称之为AOE⽹（Activity On Edge Network）

• 和AOV网的区别在于权值，AOV网的边上没有权值，它在执行任务时只考虑先后顺序

• 符合AOE网的前提条件是，必须也要符合AOV网。在有权值的同时，任务之间也要有先后顺序

名词解释：

• 由于⼀个⼯程，总有⼀个开始和⼀个结束，所以正常情况下，AOE⽹只有⼀个源点和⼀个汇点

  • 没有⼊边的顶点称为始点或源点，即：入度为0

  • 没有出边的顶点称为终点或汇点，即：出度为0

• 路径上各个活动所持续的时间之和称为路径⻓度

• 从源点到汇点具有最⼤的路径叫关键路径

• 在关键路径上的活动叫关键活动

核⼼参数：

• 事件最早发⽣的时间etv（earliest time of vertex）：即顶点Vk的最早发⽣时间

• 事件最晚发⽣时间ltv（latest time of vertex）：即顶点Vk的最晚发⽣时间，也就是每个顶点对应的事件最晚需要开始的时间，超出此时间将会延误整个⼯期

• 活动的最早开⼯时间ete（earliest time of edge）：即弧Ak的最早发⽣时间

• 活动的最晚开⼯时间lte（latest time of edge）：即弧Ak的最晚发⽣时间，也就是不推迟⼯期的最晚开⼯时间

求解etv：

• 求解事件的最早发⽣时间etv的过程，就是从头到尾去找拓扑序列的过程。所以在求解关键路径之前，我们需要调⽤⼀次拓扑排序的序列，同时计算etv和拓扑序列列表

• 公式推演：

  • 当k == 0时，顶点Vk的入度为0，故此Vk的etv也为0

  • 当入度 > 0时，需要使用入边的顶点Vi所需的etv值，加上Vi → Vk的权值。如果有多条到达Vk的弧，选择最大的etv结果

求解ltv：

• 定义ltv数组，用于存储事件最晚发⽣时间。默认使用etv中最后事件的时间填充ltv数组，然后按照拓扑排序的结果遍历顶点，并依次计算各顶点对应的ltv值

• 公式推演：

  • 当k == n - 1时，顶点Vk的出度为0，故此Vk的ltv等于etv[k]

  • 当出度 > 0时，使用出边的顶点Vi所需的ltv值，减去Vi → Vk的权值。如果有多条到达Vk的弧，选择最小的ltv结果

求解关键路径：

• ete表示活动Vk → Vj的最早开⼯时间，是针对这条弧来说的。⽽这条弧的弧尾顶点Vk的事件发⽣了，它才可以发⽣。因此ete = etv[k]

• lte表示活动Vk → Vj的最晚开⼯时间，但此活动再晚也不能等Vj事件发⽣才开始，⽽是必须在Vj事件之前发⽣。所以lte = ltv[j] - len<Vk, Vj>

• 例如，我们需要2⼩时完成作业，并且必须在23点睡觉。所以我们不能在23点才开始做作业，⽽是必须提前2⼩时在21点开始，才能按计划在23点睡觉

• 所以, 如果判断ete与lte是否相等，相等就意味着活动之间没有任何空闲时间，则它是关键活动，否则不是

• 时间复杂度

  • 拓扑排序的时间复杂度：O(n + e)

  • 初始化ltv时间复杂度：O(n)

  • 计算ltv的时间复杂度：O(n + e)

  • 计算ete、lte时间复杂度：O(n + e)

  • 所以最终求解关键路径的时间复杂度为：O(n + e)