1. 树的相关定义
1.1 树结构
树结构是一种非线性存储结构,存储的是具有“一对多”关系的数据元素的集合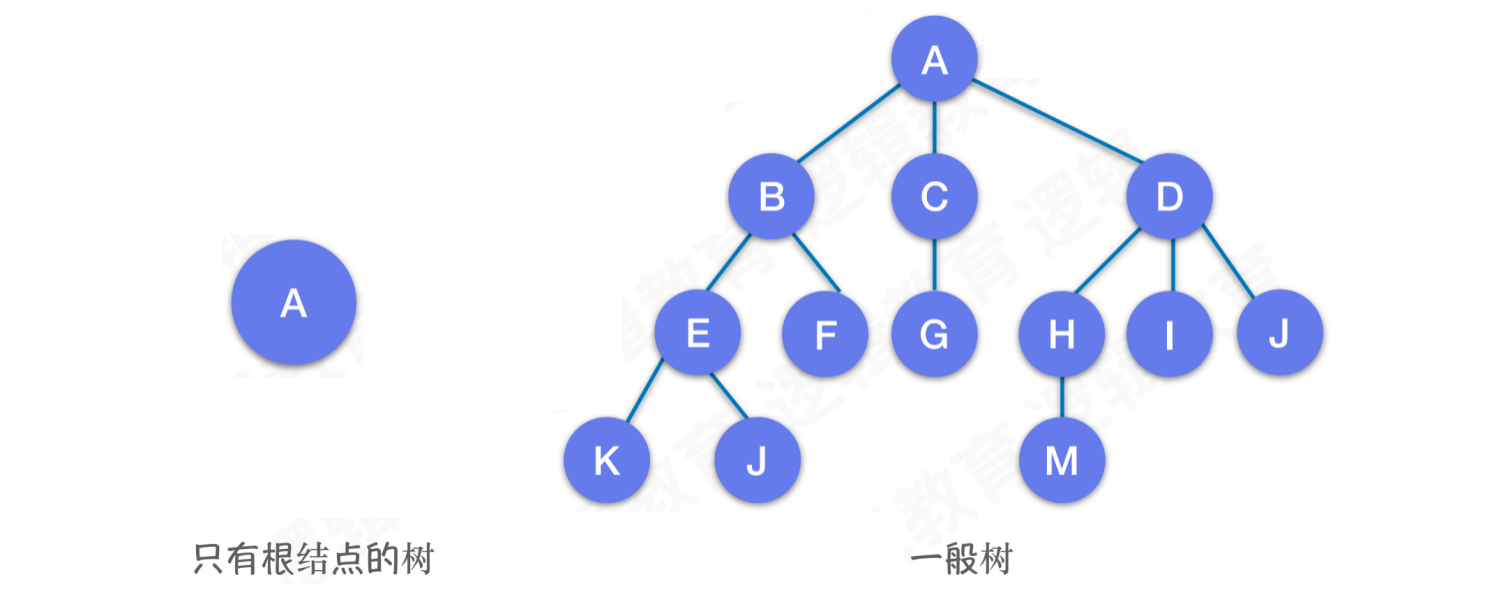
在一般树中,
A为根结点,根结点下有三个互不相交的子集子集一:
B、E、F、K、J子集二:
C、G子集三:
D、H、I、J、M
这三个子集是根结点
A的子树,它们也可以独立当做一颗树,例如:B结点是T1树的根结点
1.2 基本语数
结点:使用树结构存储的每一个数据元素都被称为“结点”
结点的度:对于一个结点,拥有的子树个数(结点有多少分支)称为结点的度(Degree)。例如: A结点下分出了三个子树,所以A结点的度为3
树的度:指树内各结点度的最⼤值。例如:上图中树的度应该为3
子结点:结点的⼦树的根称为该结点的子结点。例如:B、C、D为结点A的子结点
父结点:也称之为双亲结点,指的是一个结点。例如:结点G的父结点(双亲结点)为结点C
叶子结点:如果结点没有任何子结点,即度为0的结点,那么此结点称为叶子结点(终端结点)。例如: 结点 K、J、F、G、M、I、J都是这颗树的叶子结点
非终端结点:度大于0的结点,称之为非终端结点
兄弟结点:同属于一个父结点的多个结点,它们称之为兄弟结点。例如:结点B下的结点E和结点F互为兄弟结点
堂兄弟:双亲在同⼀层的结点互为堂兄弟结点。例如:结点G与E、F、H、I、J互为堂兄弟结点
祖先:从根到该结点所经历的分⽀上的所有结点。例如:结点M的祖先为A、D、H
⼦孙:以某结点为根的⼦树中的任意结点都称为该结点的⼦孙。例如:结点B的⼦孙为E、F
结点的高度、深度以及层数: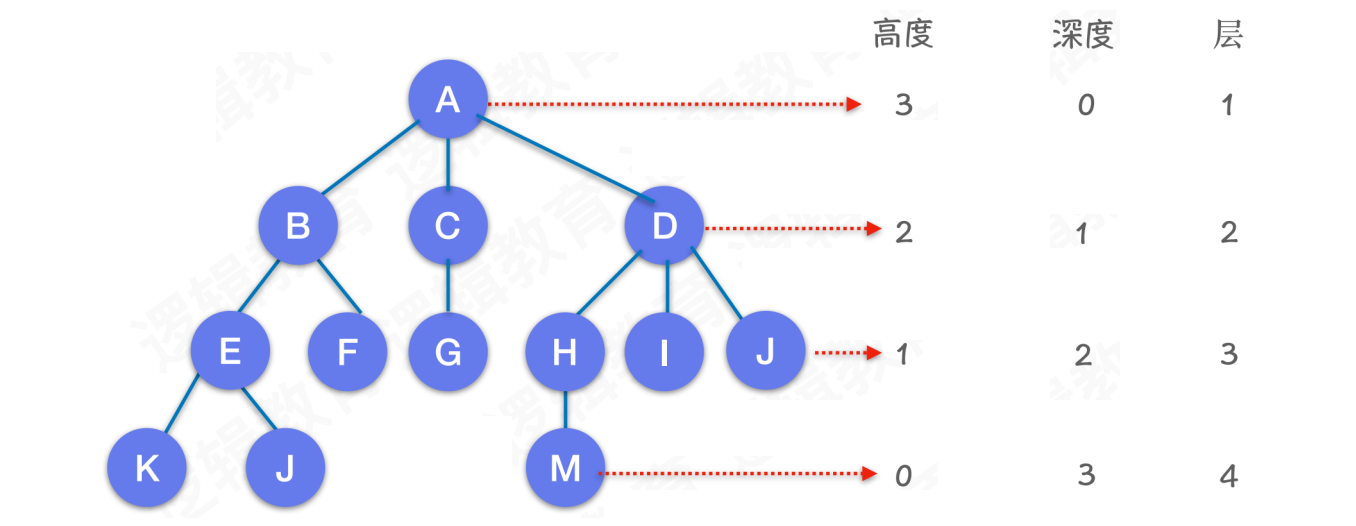
结点的⾼度:结点到叶⼦结点的最⻓路径(边数)
结点的深度:根结点到这个结点所经历的边的个数
结点的层数:结点的深度
+1树的深度(⾼度):根结点的⾼度
有序树和⽆序树:
如果将树的结点的各⼦树看成从左到右是有次序的(即不能互换),则称为该树为有序树,否则是⽆序树
在有序树中最左边的⼦树的根称为第⼀个孩⼦,最右边的称为最后⼀个孩⼦
什么叫有序树?就类似在家谱中第⼀房太太到第五房太太以及孩⼦是有顺序的,存在这样的顺序关系叫有序树
2. 二叉树的相关定义
⼆叉树(Binary Tree)是指n(n >= 0)个结点所构成的集合,它或为空树(n = 0)
对于⾮空树T,满足以下两个条件就是二叉树:
有且仅有⼀个称之为根结点
除了根结点以外的其余结点分为两个互不相交的⼦集
T1、T2,分别称为T的左⼦树和右⼦树,且T1和T2本身都是⼆叉树
二叉树: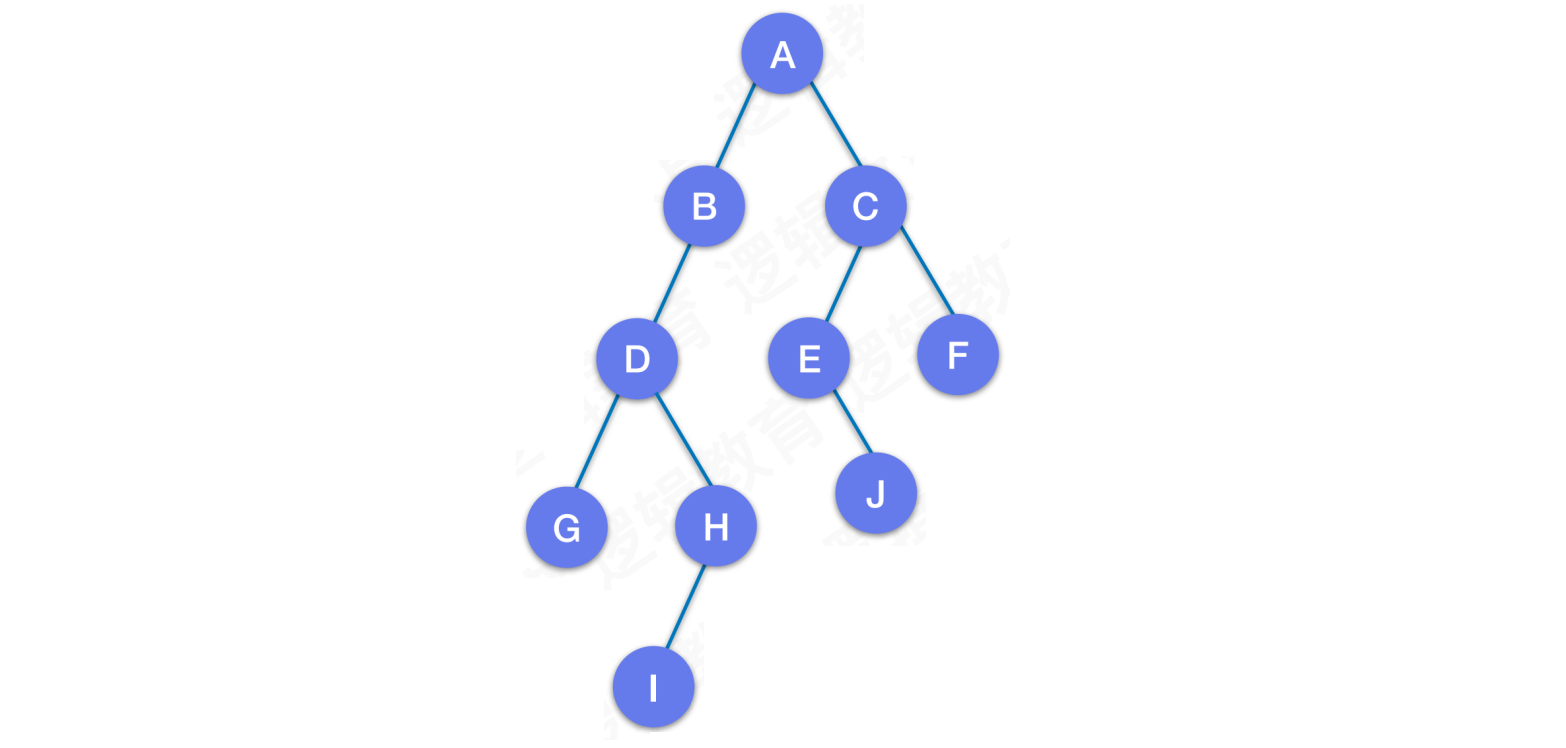
2.1 二叉树特性
⼆叉树每个结点⾄多只有两颗⼦树(⼆叉树中不存在度⼤于2的结点),所以⼆叉树中不存在⼤于2的结点
- 注意:不是只有2个⼦树,⽽是最多只有。如果⼆叉树中没有⼦树或者只有⼀颗树是可以的
⼆叉树的⼦树有左右之分,其次序不能任意颠倒。类似于⼈的双⼿、双脚,有顺序之分
即使只有⼀颗树,也需要区分是左⼦树还是右⼦树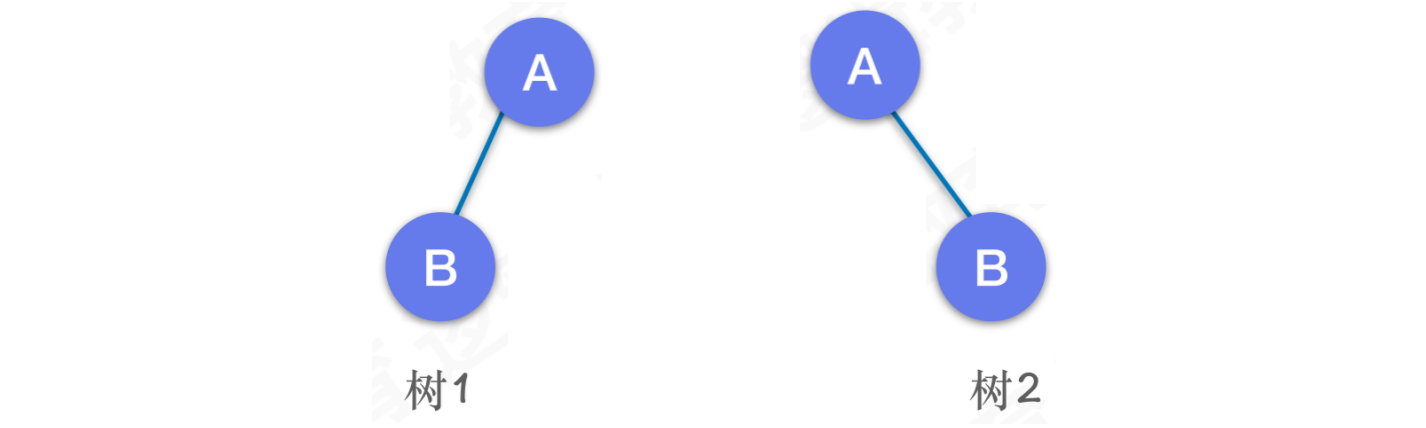
- 类似于⽣活中摔伤了⼿,伤的是左⼿还是右⼿,对⽣活的影响都是完全不同的
2.2 五种形态
二叉树的五种形态: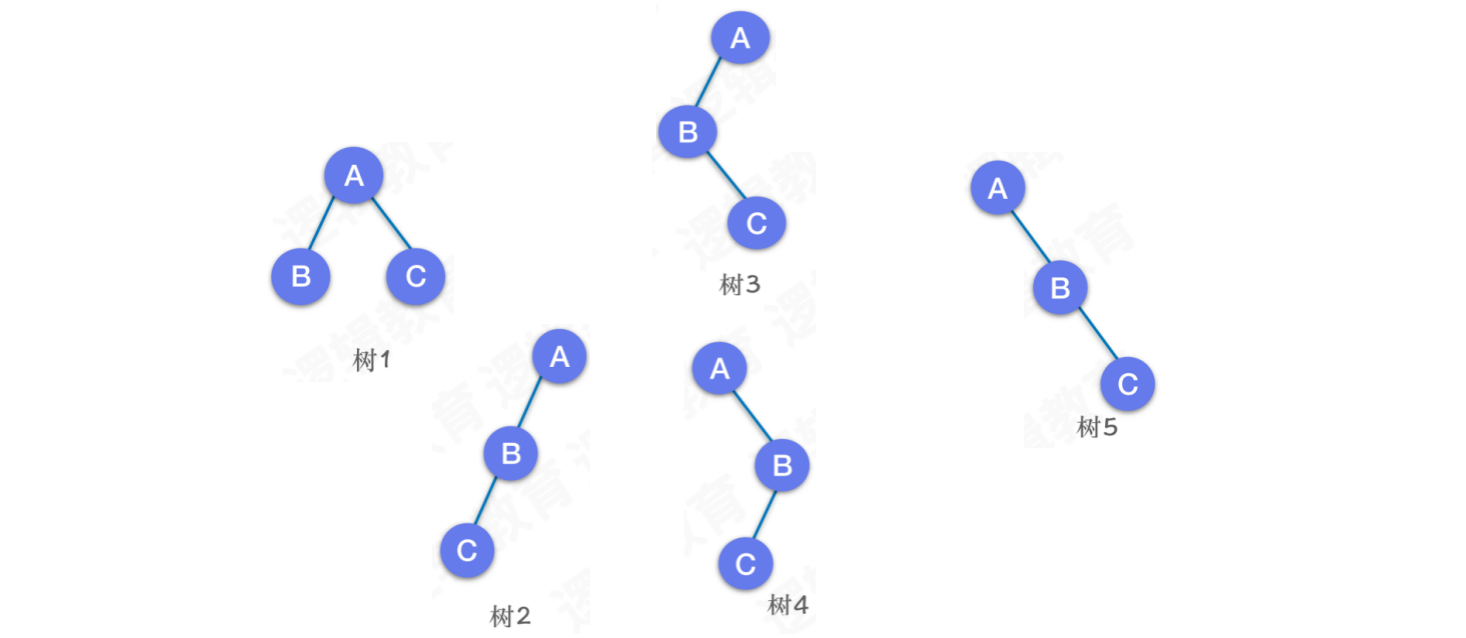
- 每颗树的形态都是不一样的,存储时要描述清楚它的逻辑意义
2.3 特殊的二叉树
2.3.1 斜树
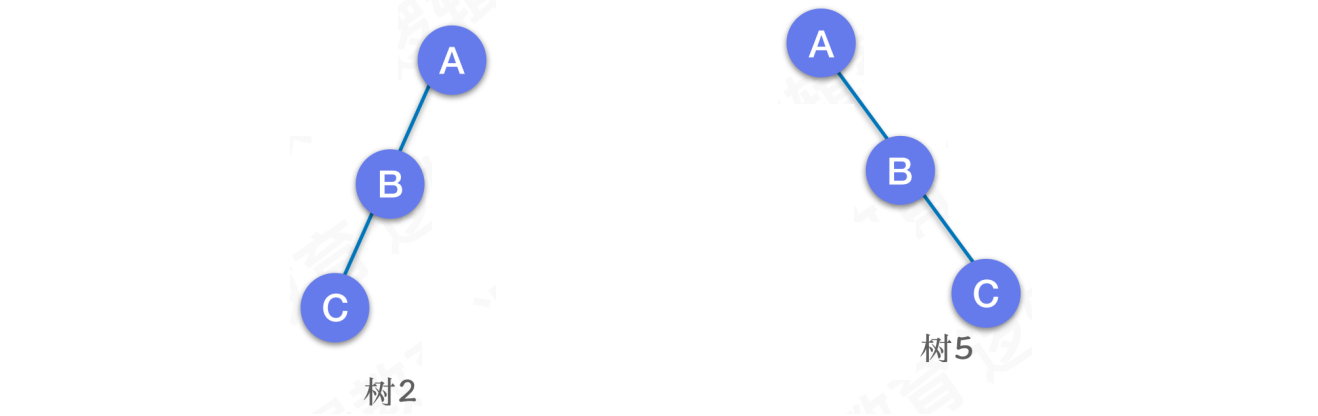
树2为左斜树,树5为右斜树,它们统称为斜树
2.3.2 满二叉树
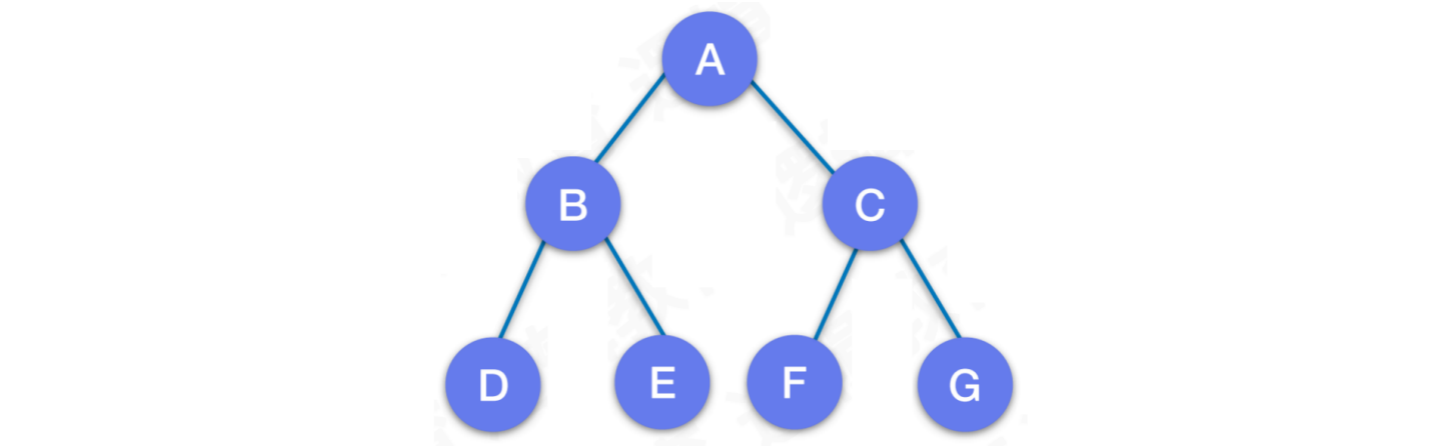
- 在一颗二叉树中,所有的分支结点都具备左子树和右子树,并且所有叶子结点都在同一层,则这颗⼆叉树称之为满二叉树
2.3.3 完全二叉树
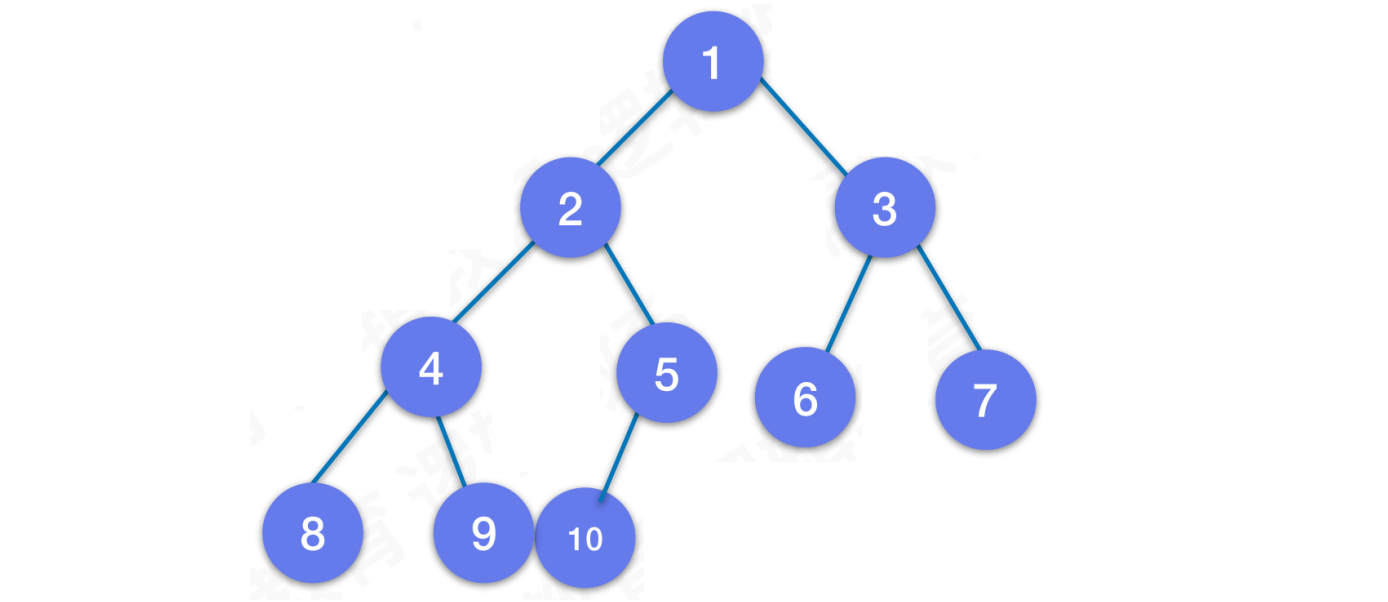
对⼀颗具有n个结点的⼆叉树按层序编号,如果编号为i(1 =< i <= n)的结点与同样深度的满⼆叉树中编号为i的结点⼆叉树中位置完全相同,则这颗⼆叉树称之为完全⼆叉树
⾸先”完全” 和 “满” 的差异,满⼆叉树⼀定是⼀个完全⼆叉树,但完全⼆叉树不⼀定是满的
完全⼆叉树的所有结点和同样深度的满⼆叉树,它们按照层序编号相同的结点⼀⼀对应
这⾥有⼀个关键词“按层序编号”:
叶⼦结点只能出现在最下两层
最下层的叶⼦⼀定集中在左部连接
倒数第⼆层若有叶⼦结点,⼀定都在右部连续位置
如果结点度为
1,则该结点只有左孩⼦,既不存在只有右⼦树的情况同样结点数的⼆叉树,完全⼆叉树的深度最⼩
完全二叉树的判断:
示例1: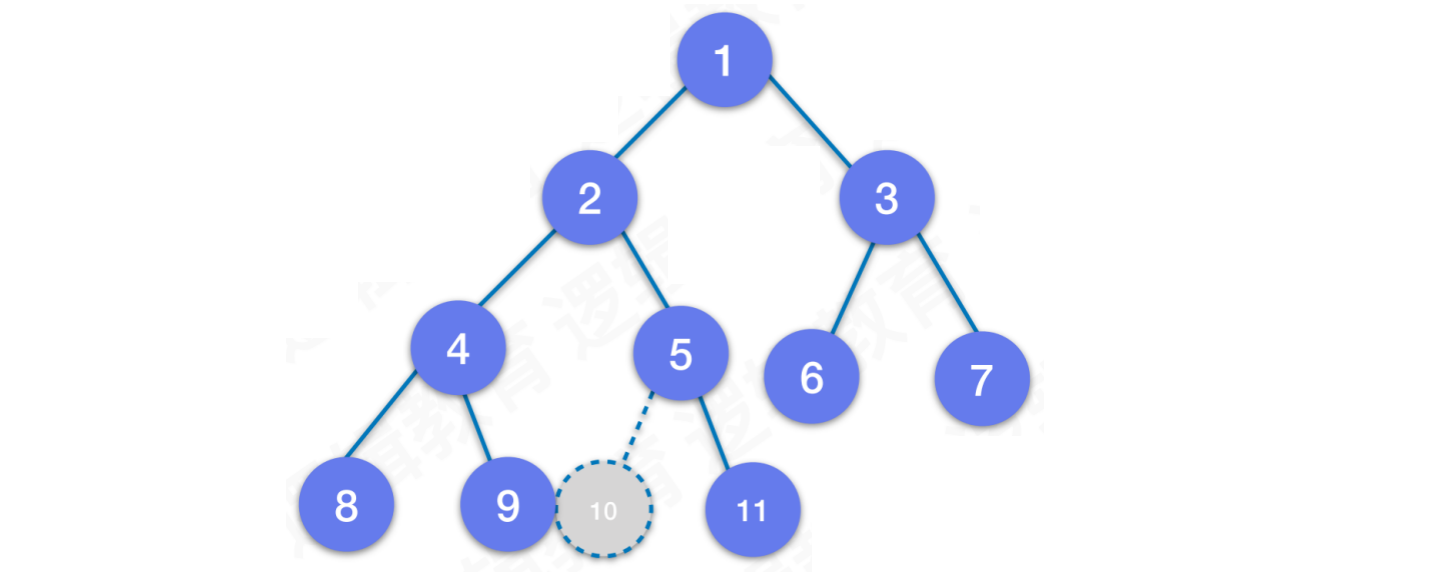
- 该二叉树不是完全⼆叉树,因为层序编号中缺少
10
示例2: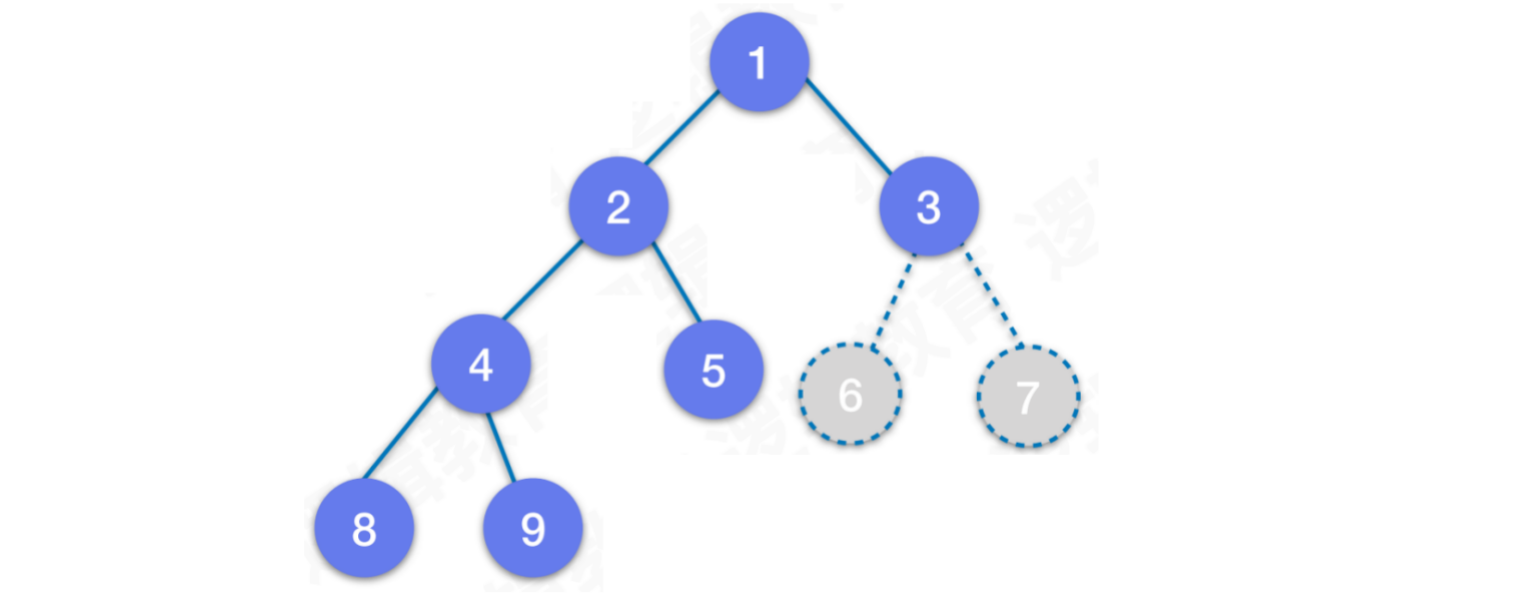
- 该二叉树不是完全⼆叉树,因为层序编号中缺少
6、7
2.4 二叉树的性质
性质1:在二叉树的第
i层上最多有2i - 1个结点性质2:深度为
K的二叉树最多有2k - 1个结点(K >= 1)性质3:对于任何一颗二叉树
T,如果其终端结点数为n0,度为2的结点数为n2,则n0 = n2 + 1性质4:具有
n个结点的完全二叉树深度为log2(n) + 1性质5:对具有
n个结点的完全二叉树,如果按照从上至下和从左至右的顺序对二
叉树的所有结点从1开始编号,则对于任意的序号为i的结点有:
如果
i > 1,那么序号为i的结点的双亲结点序号为i / 2如果
i = 1,那么序号为i的结点为根结点,无双亲结点如果
2i <= n,那么序号为i的结点的左孩子结点序号为2i如果
2i > n,那么序号为i的结点无左孩子如果
2i + 1 <= n,那么序号为i的结点右孩子序号为2i + 1如果
2i + 1 > n,那么序号为i的结点无右孩子
3. 二叉树的存储结构分析
对于二叉树的顺序存储,我们可以采用一个数组,下标对应层序编号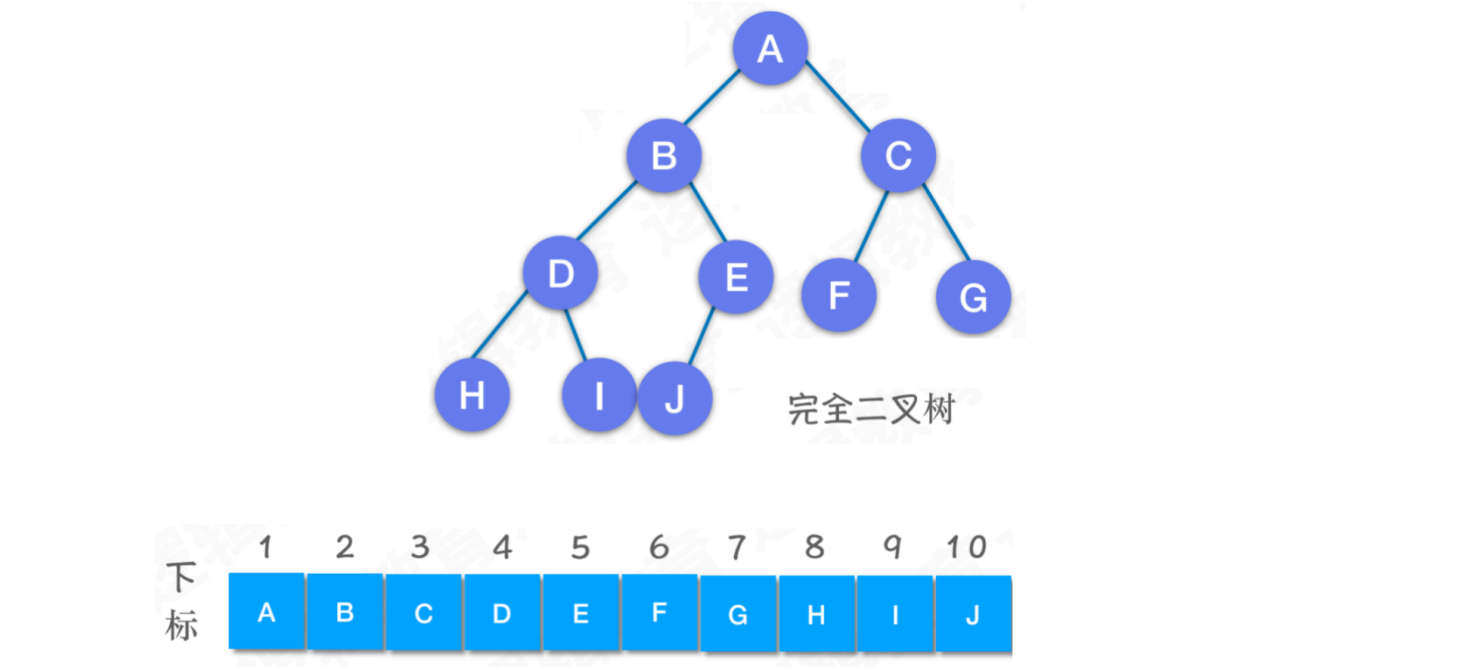
对于一颗不完全的二叉树,我们可以在数组中,将所缺少的层序编号对应的下标位置空出来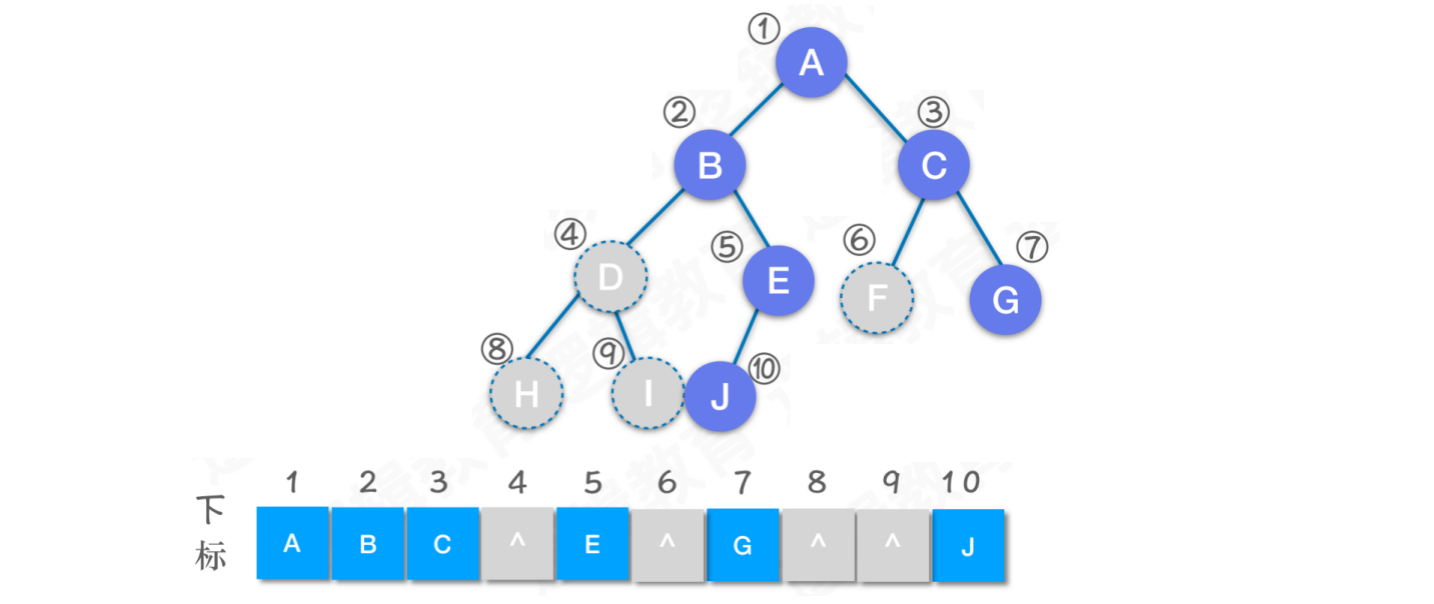
对于一颗斜树,如果使用顺序存储,就会出现大量空间浪费的情况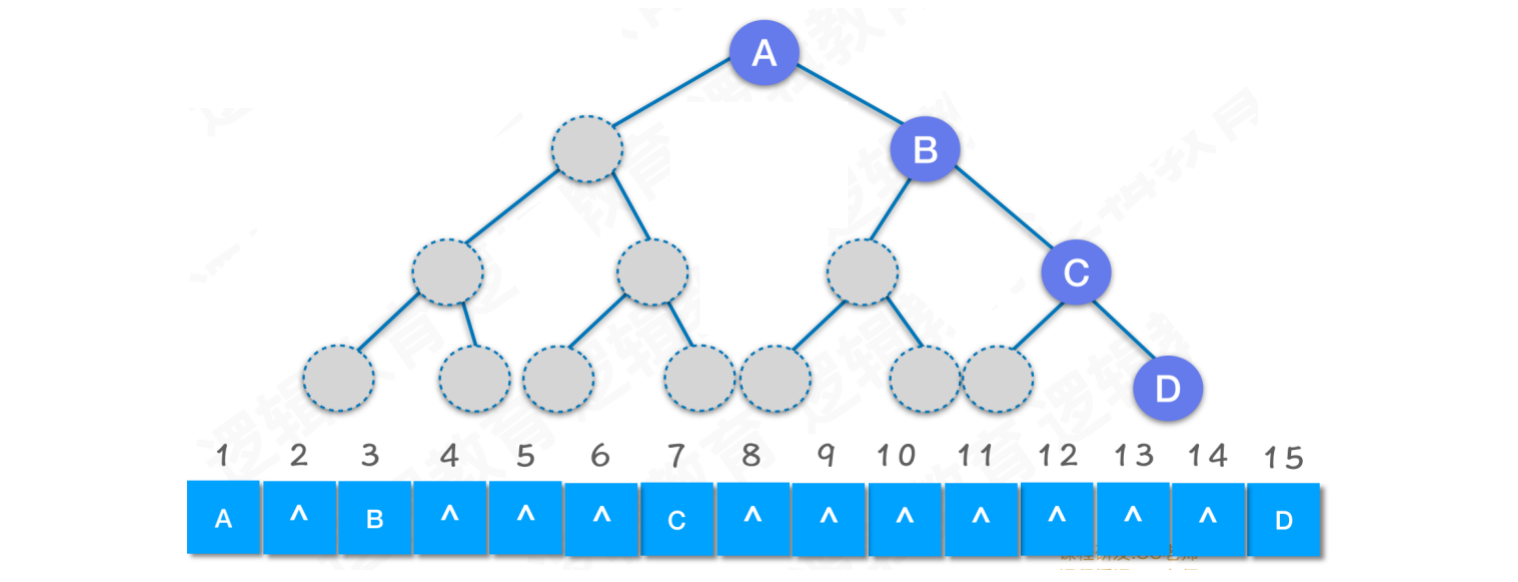
当一颗二叉树为完全二叉树,可以使用顺序存储。但对于一颗非完全二叉树,使用链式存储更合适,可以避免空间的浪费
4. 二叉树的顺序存储
4.1 创建二叉树
class LinearBiTree<Element> {fileprivate var _arr : [Element?];init(count : Int) {_arr = [Element?].init(repeating: nil, count: count);}func create(elements : [Element?]) -> Int {for index in 0 ..< elements.count {if(index != 0 && _arr[(index + 1) / 2 - 1] == nil && elements[index] != nil){print("发现没有双亲的非根结点");return ERROR;}_arr[index] = elements[index];}return OK;}func clear() {for i in 0 ..< _arr.count {_arr[i] = nil;}}}var biTree = LinearBiTree<Int>(count: 10);biTree.create(elements: [1, 2, 3]);
4.2 空树 & 结点数 & 深度
class LinearBiTree<Element> {
func isEmpty() -> Bool {
return _arr.first == nil;
}
var length : Int {
get{
if(isEmpty()){
return 0;
}
var nullity = 0;
for e in _arr.reversed() {
if(e != nil){
break;
}
nullity += 1;
}
return _arr.count - nullity;
}
};
var depth : Int {
get{
if(isEmpty()){
return 0;
}
var depth = 0;
while(Int(pow(2, Double(depth))) <= length){
depth += 1;
}
return depth;
}
};
}
4.3 添加元素
class Position {
var level : Int;
var order : Int;
init(level : Int, order : Int) {
self.level = level;
self.order = order;
}
}
class LinearBiTree<Element> {
func setElem(element : Element?, position : Position) -> Int {
let order = Int(pow(Double(2), Double(position.level - 1)));
let locate = order + position.order;
let index = locate - 2;
if(index > 0 && _arr[(index + 1) / 2 - 1] == nil){
print("发现没有双亲的非根结点");
return ERROR;
}
_arr[index] = element;
return OK;
}
}
4.4 获取元素
class LinearBiTree<Element> {
func getElem(position : Position) -> Element? {
if(isEmpty()){
return nil;
}
let order = Int(pow(Double(2), Double(position.level - 1)));
let locate = order + position.order;
if(locate > length){
return nil;
}
return _arr[locate - 2];
}
}
4.5 双亲结点、左孩子、右孩子
class LinearBiTree<Element> {
func getParents(position : Position) -> Element? {
let order = Int(pow(Double(2), Double(position.level - 1)));
let locate = order + position.order;
let index = locate - 2;
let parentsIndex = (index + 1) / 2 - 1;
return _arr[parentsIndex];
}
func getLeftChild(position : Position) -> Element? {
let order = Int(pow(Double(2), Double(position.level)));
let locate = order + position.order * 2 - 1;
let index = locate - 2;
return _arr[index];
}
func getRightChild(position : Position) -> Element? {
let order = Int(pow(Double(2), Double(position.level)));
let locate = order + position.order * 2;
let index = locate - 2;
return _arr[index];
}
}
5. 二叉树的遍历
⼆叉树的遍历(Traversing Binary Tree)是指的从根结点出发,按照某种次序依次访问⼆叉树中所有结点,使得每个结点被访问⼀次且仅被访问⼀次
二叉树的遍历,分为深度遍历和广度遍历
深度优先遍历:对每一个可能的分支路径深入到不能再深入为止,而且每个结点只能访问一次。对每一个可能的分支路径深入到不能再深入为止,而且每个结点只能访问一次
广度优先遍历:又叫层序遍历,若⼆叉树为空,则空操作返回。否则从树的第⼀层,也是就是根结点开始访问,从上⽽下逐层遍历。在同⼀层中,按从左到右的顺序对结点逐个访问
其中深度优先遍历比较特殊,可以细分为前序遍历、中序遍历以及后序遍历
前序遍历:若⼆叉树为空,则空操作返回。否则先访问根结点,然后前序遍历左⼦树,在前序遍历右⼦树
中序遍历:若⼆叉树为空,则空操作返回。否则从根结点开始(注意并不是先访问根结点),中序遍历根结点的左⼦树,然后是访问根结点,最后中序遍历右⼦树
后序遍历:若⼆叉树为空,则空操作返回。否则从左到右先叶⼦后结点的⽅式遍历左右⼦树,最后访问根结点
5.1 前序遍历
规则:若⼆叉树为空,则空操作返回。否则先访问根结点,然后前序遍历左⼦树,在前序遍历右⼦树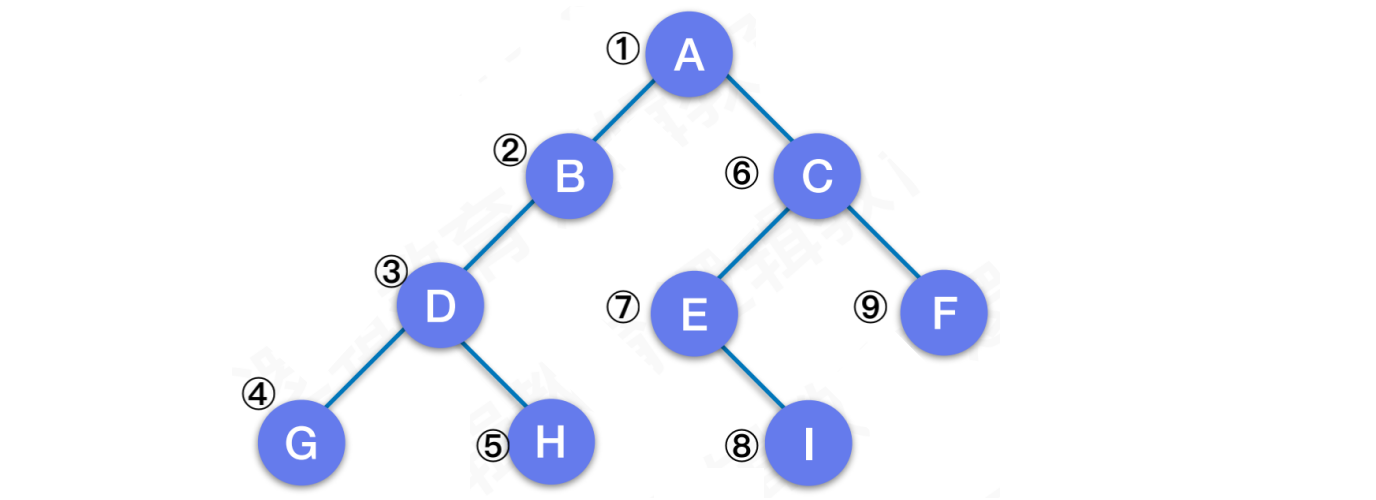
代码实现:
class LinearBiTree<Element> {
func preOrderTraverse() -> String {
var str : String = "";
if(isEmpty()){
return str;
}
preOrderTraverse(str: &str, e: 0);
return str;
}
fileprivate func preOrderTraverse(str : inout String, e : Int) {
str += "\(_arr[e]!), ";
let leftIndex = 2 * e + 1;
if(leftIndex < length && _arr[leftIndex] != nil){
preOrderTraverse(str: &str, e: leftIndex);
}
let rightIndex = 2 * e + 2;
if(rightIndex < length && _arr[rightIndex] != nil){
preOrderTraverse(str: &str, e: rightIndex);
}
}
}
5.2 中序遍历
规则:若⼆叉树为空,则空操作返回。否则从根结点开始(注意并不是先访问根结点),中序遍历根结点的左⼦树,然后是访问根结点,最后中序遍历右⼦树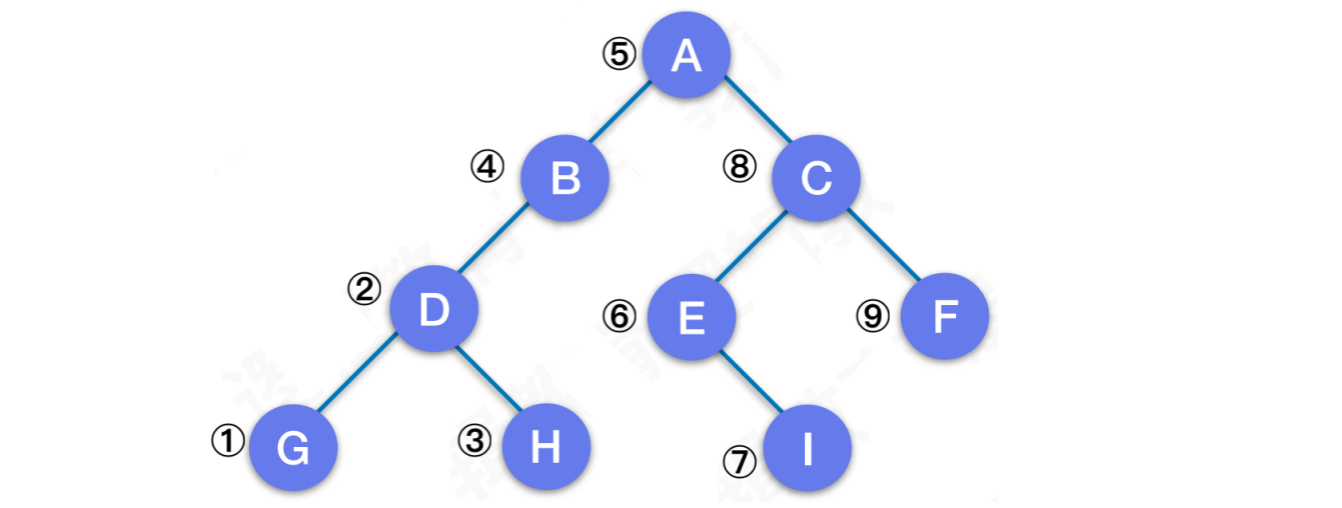
代码实现:
class LinearBiTree<Element> {
func inOrderTraverse() -> String {
var str : String = "";
if(isEmpty()){
return str;
}
inOrderTraverse(str: &str, e: 0);
return str;
}
fileprivate func inOrderTraverse(str : inout String, e : Int) {
let leftIndex = 2 * e + 1;
if(leftIndex < length && _arr[leftIndex] != nil){
inOrderTraverse(str: &str, e: leftIndex);
}
str += "\(_arr[e]!), ";
let rightIndex = 2 * e + 2;
if(rightIndex < length && _arr[rightIndex] != nil){
inOrderTraverse(str: &str, e: rightIndex);
}
}
}
5.3 后序遍历
规则:若⼆叉树为空,则空操作返回。否则从左到右先叶⼦后结点的⽅式遍历左右⼦树,最后访问根结点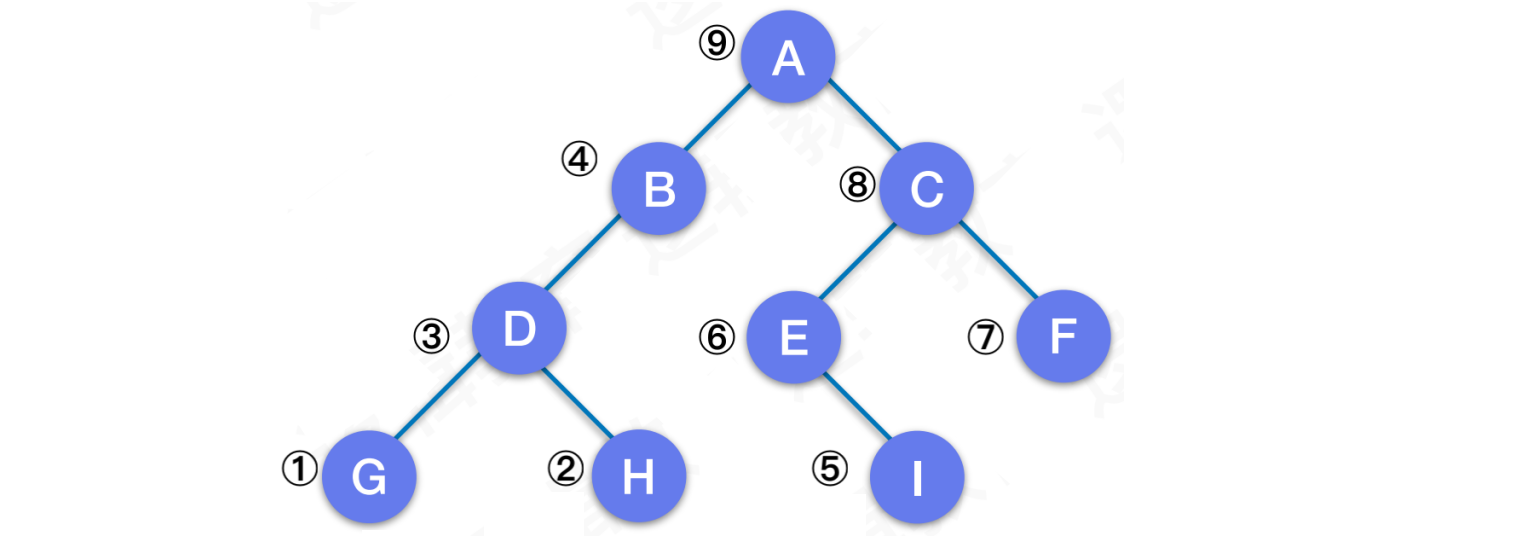
代码实现:
class LinearBiTree<Element> {
func postOrderTraverse() -> String {
var str : String = "";
if(isEmpty()){
return str;
}
postOrderTraverse(str: &str, e: 0);
return str;
}
fileprivate func postOrderTraverse(str : inout String, e : Int) {
let leftIndex = 2 * e + 1;
if(leftIndex < length && _arr[leftIndex] != nil){
postOrderTraverse(str: &str, e: leftIndex);
}
let rightIndex = 2 * e + 2;
if(rightIndex < length && _arr[rightIndex] != nil){
postOrderTraverse(str: &str, e: rightIndex);
}
str += "\(_arr[e]!), ";
}
}
5.4 层序遍历
规则:若⼆叉树为空,则空操作返回。否则从树的第⼀层,也是就是根结点开始访问,从上⽽下逐层遍历。在同⼀层中,按从左到右的顺序对结点逐个访问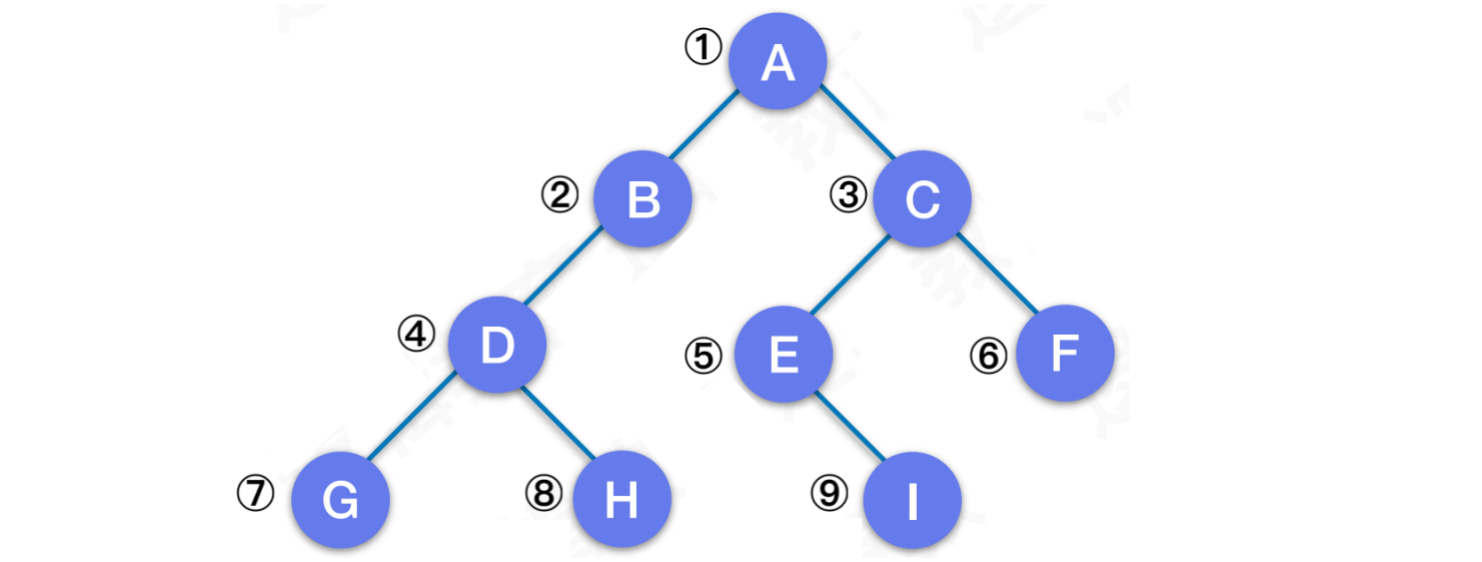
代码实现:
class LinearBiTree<Element> {
func levelOrderTraverse() -> String {
var str : String = "";
if(isEmpty()){
return str;
}
for i in 0 ..< length {
if(_arr[i] == nil){
continue;
}
str += "\(_arr[i]!), "
}
return str;
}
}
6. 二叉树的链式存储
6.1 创建二叉树
创建以下结构二叉树: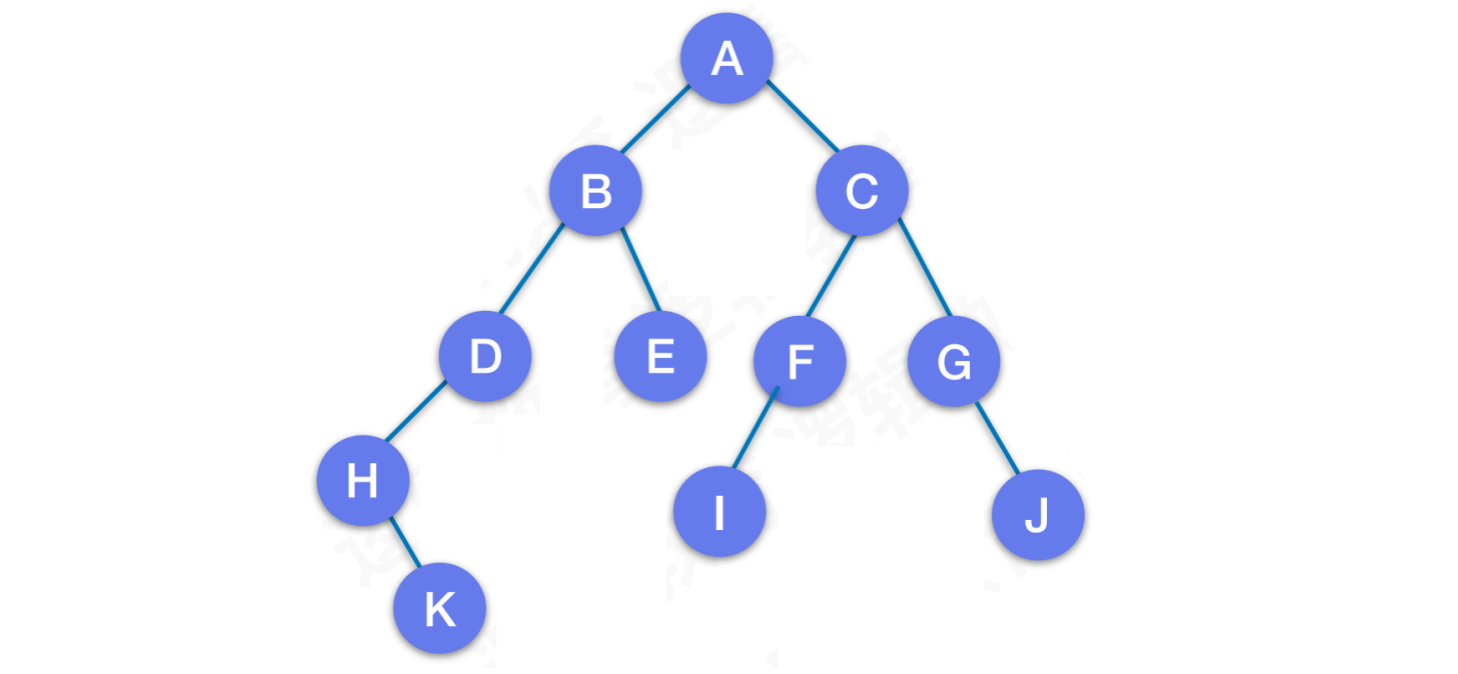
使用链式存储,必须确定每个结点是否有左右孩子,我们可以对其进行扩展。将普通二叉树结点中的空结点,使用默认元素进行填充,例如:以#填充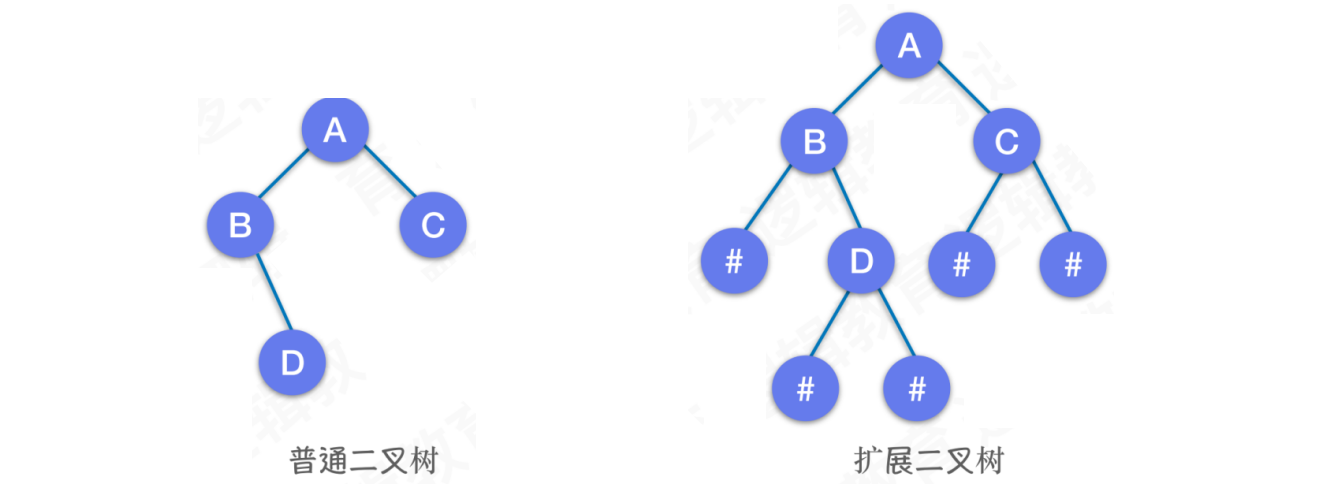
将需求中的普通二叉树,填充为扩展二叉树: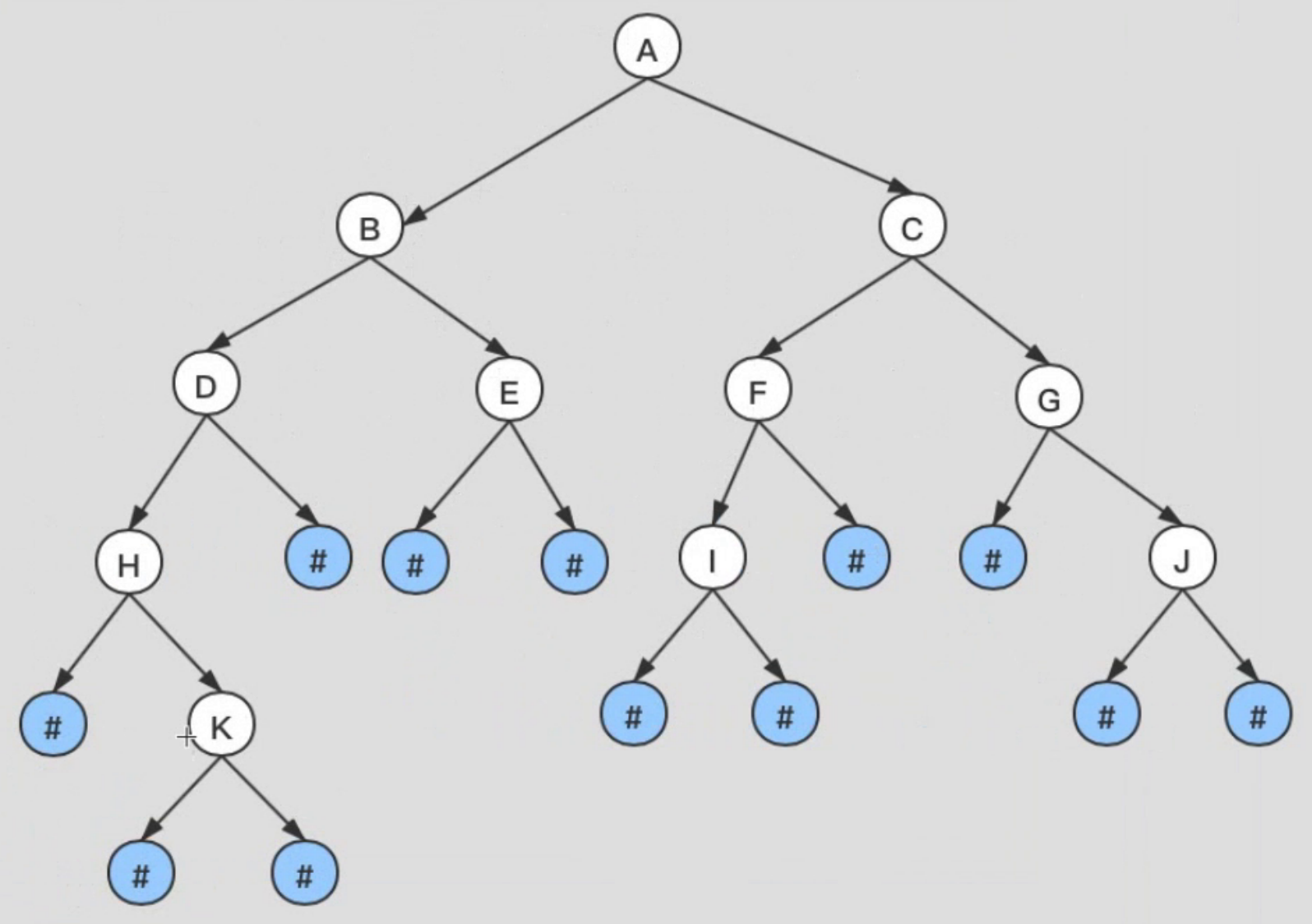
代码实现:
public struct LinkedBiTree {
fileprivate class BiTNode {
var data : Character;
var leftChild : BiTNode?;
var rightChild : BiTNode?;
init(c : Character){
self.data = c;
self.leftChild = nil;
self.rightChild = nil;
}
deinit {
print("值为\(data)的Node释放");
}
}
fileprivate var _root : BiTNode? = nil;
init(str : String){
var index = 0;
var root : BiTNode?;
createTree(str: str, index: &index, node: &root);
}
fileprivate mutating func createTree(str : String, index : inout Int, node : inout BiTNode?){
let c = str[index];
if(c == "#"){
node = nil;
return;
}
node = BiTNode(c: Character(c));
if(index == 0){
_root = node;
}
index += 1;
if(index >= str.count){
return;
}
createTree(str: str, index: &index, node: &node!.leftChild);
index += 1;
if(index >= str.count){
return;
}
createTree(str: str, index: &index, node: &node!.rightChild);
}
}
var biTree = LinkedBiTree(str: "ABDH#K###E##CFI###G#J");
6.2 空树 & 深度
public struct LinkedBiTree {
var depth : Int {
get{
if(isEmpty()){
return 0;
}
return getDepth(node: _root);
}
};
fileprivate func getDepth(node : BiTNode?) -> Int {
var leftCount = 0;
var rightCount = 0;
if(node?.leftChild != nil){
leftCount = getDepth(node: node?.leftChild);
}
else{
leftCount = 0;
}
if(node?.rightChild != nil){
rightCount = getDepth(node: node?.rightChild);
}
else{
rightCount = 0;
}
return leftCount > rightCount ? leftCount + 1 : rightCount + 1;
}
func isEmpty() -> Bool {
return _root == nil;
}
}
6.3 深度优先遍历
实现二叉树的深度优先遍历(前序、中序、后续),可以使用递归或非递归方式。非递归方式,需要使用栈结构作为辅助
6.3.1 递归方式
public struct LinkedBiTree {
func preOrderTraverse() -> String {
var str : String = "";
if(isEmpty()){
return str;
}
preOrderTraverse(str: &str, node: _root);
return str;
}
fileprivate func preOrderTraverse(str : inout String, node : BiTNode?) {
str += "\(String(node!.data)), ";
if(node?.leftChild != nil){
preOrderTraverse(str: &str, node: node?.leftChild);
}
if(node?.rightChild != nil){
preOrderTraverse(str: &str, node: node?.rightChild);
}
}
func inOrderTraverse() -> String {
var str : String = "";
if(isEmpty()){
return str;
}
inOrderTraverse(str: &str, node: _root);
return str;
}
fileprivate func inOrderTraverse(str : inout String, node : BiTNode?) {
if(node?.leftChild != nil){
inOrderTraverse(str: &str, node: node?.leftChild);
}
str += "\(String(node!.data)), ";
if(node?.rightChild != nil){
inOrderTraverse(str: &str, node: node?.rightChild);
}
}
func postOrderTraverse() -> String {
var str : String = "";
if(isEmpty()){
return str;
}
postOrderTraverse(str: &str, node: _root);
return str;
}
fileprivate func postOrderTraverse(str : inout String, node : BiTNode?) {
if(node?.leftChild != nil){
postOrderTraverse(str: &str, node: node?.leftChild);
}
if(node?.rightChild != nil){
postOrderTraverse(str: &str, node: node?.rightChild);
}
str += "\(String(node!.data)), ";
}
}
6.3.1 栈结构方式
public struct LinkedBiTree {
// 前序遍历-栈
func preOrderWithStack() -> String {
var str = "";
if(_root == nil){
return str;
}
let stack = LinkedStack<BiTNode>();
var node = _root;
while(node != nil || !stack.isEmpty()){
while(node != nil){
str += "\(node!.data)";
stack.push(element: node!);
node = node?.leftChild;
}
if(!stack.isEmpty()){
node = stack.pop();
node = node?.rightChild;
}
}
return str;
}
// 中序遍历-栈
func inOrderWithStack() -> String {
var str = "";
if(_root == nil){
return str;
}
let stack = LinkedStack<BiTNode>();
var node = _root;
while(node != nil || !stack.isEmpty()){
while(node != nil){
stack.push(element: node!);
node = node?.leftChild;
}
if(!stack.isEmpty()){
node = stack.pop();
str += "\(node!.data)";
node = node?.rightChild;
}
}
return str;
}
// 后序遍历-栈
func postOrderWithStack() -> String {
var str = "";
if(_root == nil){
return str;
}
let stack = LinkedStack<BiTNode>();
var node = _root;
var finishNode = _root;
while(node != nil || !stack.isEmpty()){
while(node != nil){
stack.push(element: node!);
node = node?.leftChild;
}
node = stack.getTop();
if(node?.rightChild != nil && node?.rightChild?.data != finishNode?.data){
node = node?.rightChild;
continue;
}
str += "\(node!.data)";
stack.pop();
finishNode = node;
node = nil;
}
return str;
}
}
6.4 广度优先遍历
实现链式存储二叉树的广度优先遍历,需要使用队列作为辅助
public struct LinkedBiTree {
// 层序遍历-队列
func levelOrderTraverse() -> String {
var str = "";
if(_root == nil){
return str;
}
let queue = LinkedQueue<BiTNode>();
queue.enter(element: _root!);
while(!queue.isEmpty()){
let node = queue.out();
str += "\(node!.data)";
if(node?.leftChild != nil){
queue.enter(element: node!.leftChild!);
}
if(node?.rightChild != nil){
queue.enter(element: node!.rightChild!);
}
}
return str;
}
}
总结
树结构:
- 树结构是一种非线性存储结构,存储的是具有“一对多”关系的数据元素的集合
基本语数:
结点:使用树结构存储的每一个数据元素都被称为“结点”
结点的度:对于一个结点,拥有的子树个数(结点有多少分支)称为结点的度(
Degree)树的度:指树内各结点度的最⼤值
子结点:结点的⼦树的根称为该结点的子结点
父结点:也称之为双亲结点,指的是一个结点
叶子结点:如果结点没有任何子结点,即度为
0的结点,那么此结点称为叶子结点(终端结点)非终端结点:度大于
0的结点,称之为非终端结点兄弟结点:同属于一个父结点的多个结点,它们称之为兄弟结点
堂兄弟:双亲在同⼀层的结点互为堂兄弟结点
祖先:从根到该结点所经历的分⽀上的所有结点
⼦孙:以某结点为根的⼦树中的任意结点都称为该结点的⼦孙
结点的⾼度:结点到叶⼦结点的最⻓路径(边数)
结点的深度:根结点到这个结点所经历的边的个数
结点的层数:结点的深度
+1树的深度(⾼度):根结点的⾼度
二叉树的相关定义:
⼆叉树(
Binary Tree)是指n(n >= 0)个结点所构成的集合,它或为空树(n = 0)对于⾮空树
T,满足以下两个条件就是二叉树:有且仅有⼀个称之为根结点
除了根结点以外的其余结点分为两个互不相交的⼦集
T1、T2,分别称为T的左⼦树和右⼦树,且T1和T2本身都是⼆叉树
特殊的二叉树:
左斜树与右斜树,统称为斜树
在一颗二叉树中,所有的分支结点都具备左子树和右子树,并且所有叶子结点都在同一层,则这颗⼆叉树称之为满二叉树
对⼀颗具有
n个结点的⼆叉树按层序编号,如果编号为i(1 =< i <= n)的结点与同样深度的满⼆叉树中编号为i的结点⼆叉树中位置完全相同,则这颗⼆叉树称之为完全⼆叉树⾸先”完全” 和 “满” 的差异,满⼆叉树⼀定是⼀个完全⼆叉树,但完全⼆叉树不⼀定是满的
完全⼆叉树的所有结点和同样深度的满⼆叉树,它们按照层序编号相同的结点⼀⼀对应
二叉树的存储结构分析:
对于二叉树的顺序存储,我们可以采用一个数组,下标对应层序编号
对于一颗不完全的二叉树,我们可以在数组中,将所缺少的层序编号对应的下标位置空出来
对于一颗斜树,如果使用顺序存储,就会出现大量空间浪费的情况
当一颗二叉树为完全二叉树,可以使用顺序存储。但对于一颗非完全二叉树,使用链式存储更合适,可以避免空间的浪费
二叉树的遍历:
分为深度遍历和广度遍历:
深度优先遍历:对每一个可能的分支路径深入到不能再深入为止,而且每个结点只能访问一次。对每一个可能的分支路径深入到不能再深入为止,而且每个结点只能访问一次
广度优先遍历:又叫层序遍历,若⼆叉树为空,则空操作返回。否则从树的第⼀层,也是就是根结点开始访问,从上⽽下逐层遍历。在同⼀层中,按从左到右的顺序对结点逐个访问
其中深度优先遍历比较特殊,可以细分为前序遍历、中序遍历以及后序遍历
前序遍历:若⼆叉树为空,则空操作返回。否则先访问根结点,然后前序遍历左⼦树,在前序遍历右⼦树
中序遍历:若⼆叉树为空,则空操作返回。否则从根结点开始(注意并不是先访问根结点),中序遍历根结点的左⼦树,然后是访问根结点,最后中序遍历右⼦树
后序遍历:若⼆叉树为空,则空操作返回。否则从左到右先叶⼦后结点的⽅式遍历左右⼦树,最后访问根结点

