1. 数据结构
- 数据结构:指的数据对象中的数据元素之间的关系
1.1 基本数据单位
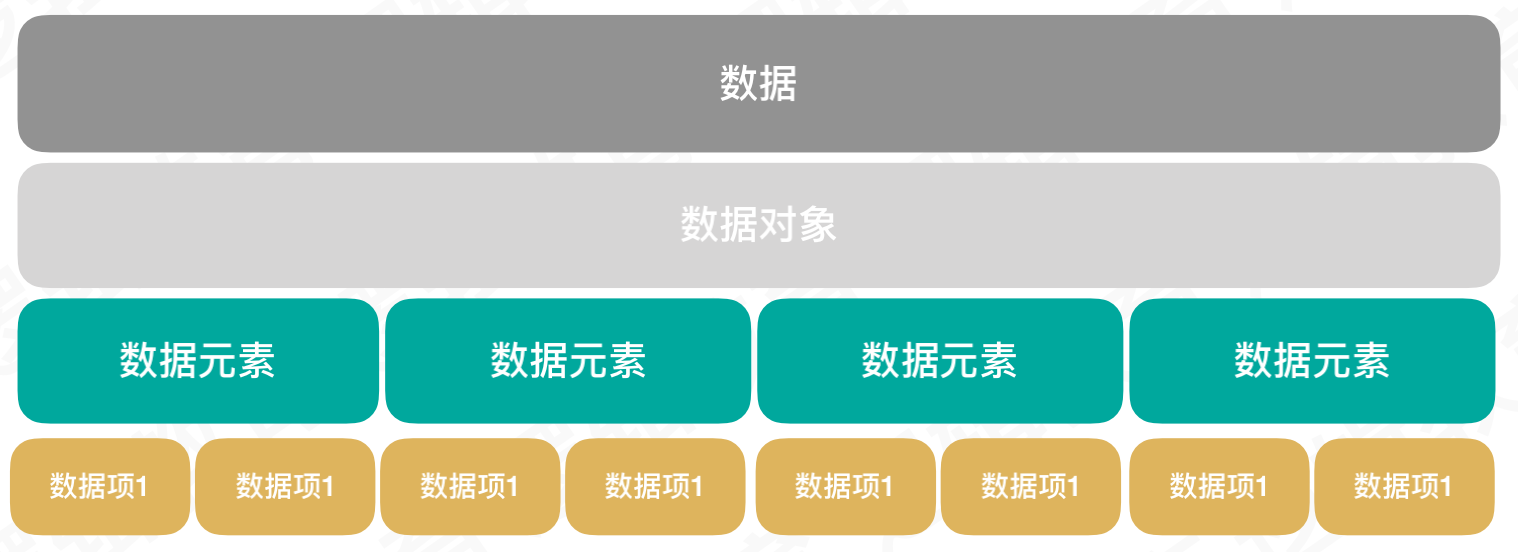
数据:程序的操作对象,用于描述客观事务
数据的特点:
可以输入到计算机
可以被计算机处理
数据对象:性质相同的数据元素的集合,类似于数组
数据元素:组成数据对象的基本单位
数据项:一个数据元素由若干数据项组成
案例:
#include <stdio.h>//声明一个结构体类型struct Teacher{ //一种数据结构char *name; //数据项--名字char *title; //数据项--职称int age; //数据项--年龄};int main(int argc, const char * argv[]) {struct Teacher t1; //数据元素;struct Teacher tArray[10]; //数据对象;t1.age = 18; //数据项t1.name = "CC"; //数据项t1.title = "讲师"; //数据项return 0;}
1.2 存储结构
结构:数据元素之间不是独立的,存在特定的关系,这些关系即是结构
分析数据结构时,一般有两种视角:
逻辑结构:描述数据与数据之间的逻辑关系
物理结构:数据存储在磁盘中的方式
1.2.1 逻辑结构
集合结构:
- 特点:所有数据都属于同一集合,元素之间平等,没有顺序。例如:
OC中的NSSet
线性结构: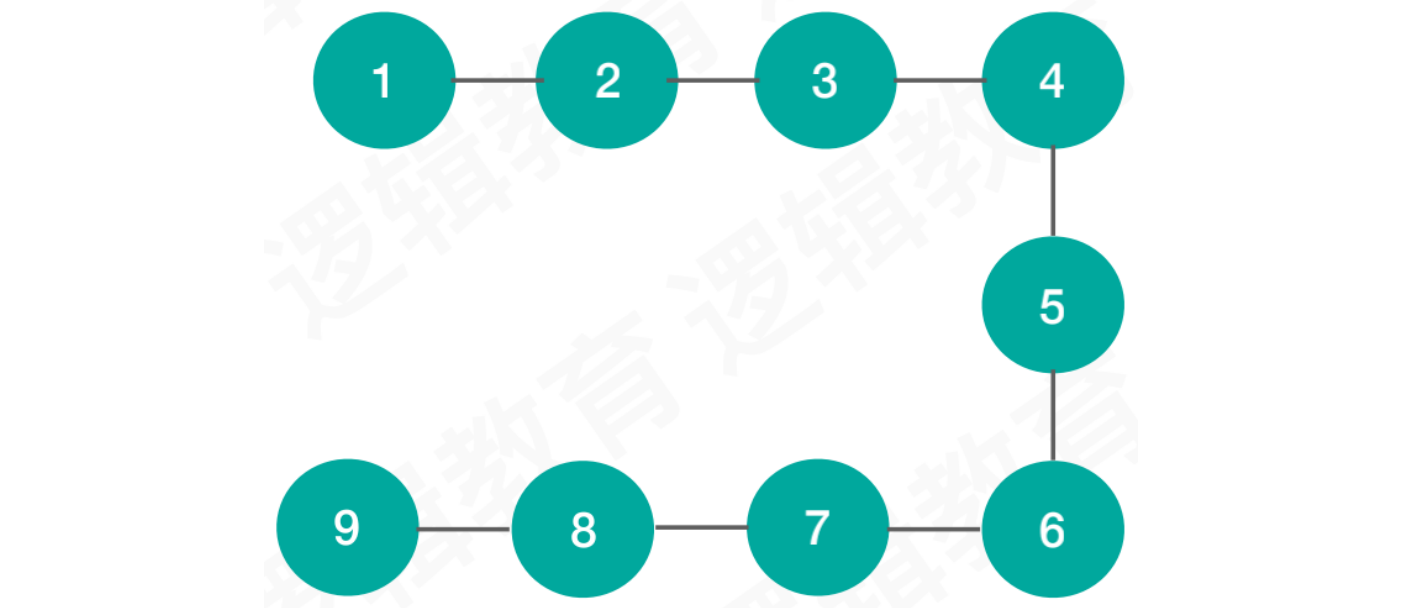
特点:数据之间是一对一的关系。例如,线性表、数组、队列、栈、字符串等
其中队列和栈属于特殊的线性结构,因为满足数据一对一关系。它们的特殊在于读取方式,队列为先进先出,栈为先进后出
字符串也属于特殊的线性结构,它由
N个字符组成,满足数据一对一关系。它的特殊在于只能存储字符串
树形结构: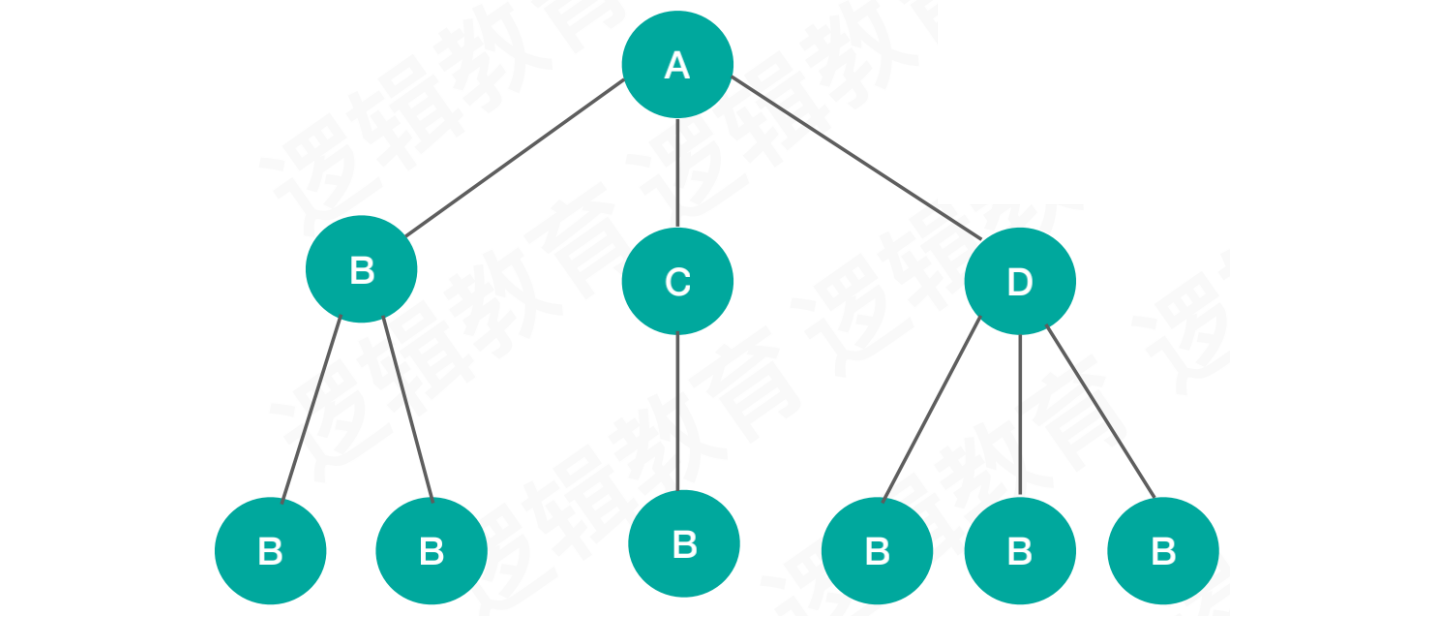
- 特点:数据之间是一对多的关系。例如:二叉树、B树、多路树、红黑树、平衡二叉树等
图形结构: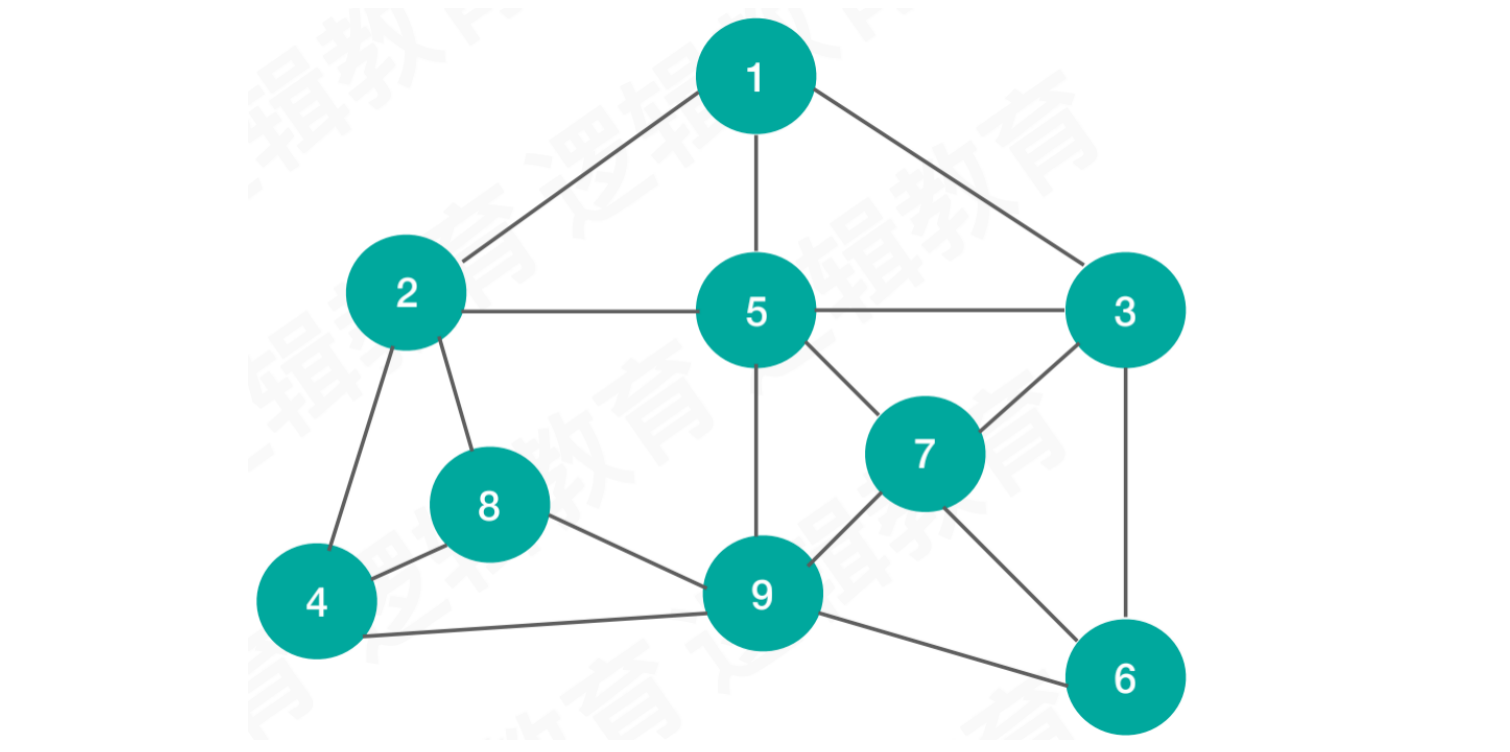
特点:数据之间多对多的结构。例如:邻接矩阵、邻接表
1.2.2 物理结构
顺序存储结构:
特定:开辟一段连续的内存空间,数据依次存储。例如:数组
缺陷:当插入、删除元素时,除了操作指定位置的元素之外,还要将后面的元素移动位置
链式存储结构:
特定:不需要提前开辟连续空间。例如:链表
缺陷:查找元素时需要进行遍历操作
2. 算法
算法:指解决特定问题求解步骤的描述。在计算机中表现为指令的有限序列,并且每个指令表示一个或多个操作
2.1 算法与数据结构的关系
数据结构与算法二者是不可分割的
例如:我们需要炒一盘酸辣土豆丝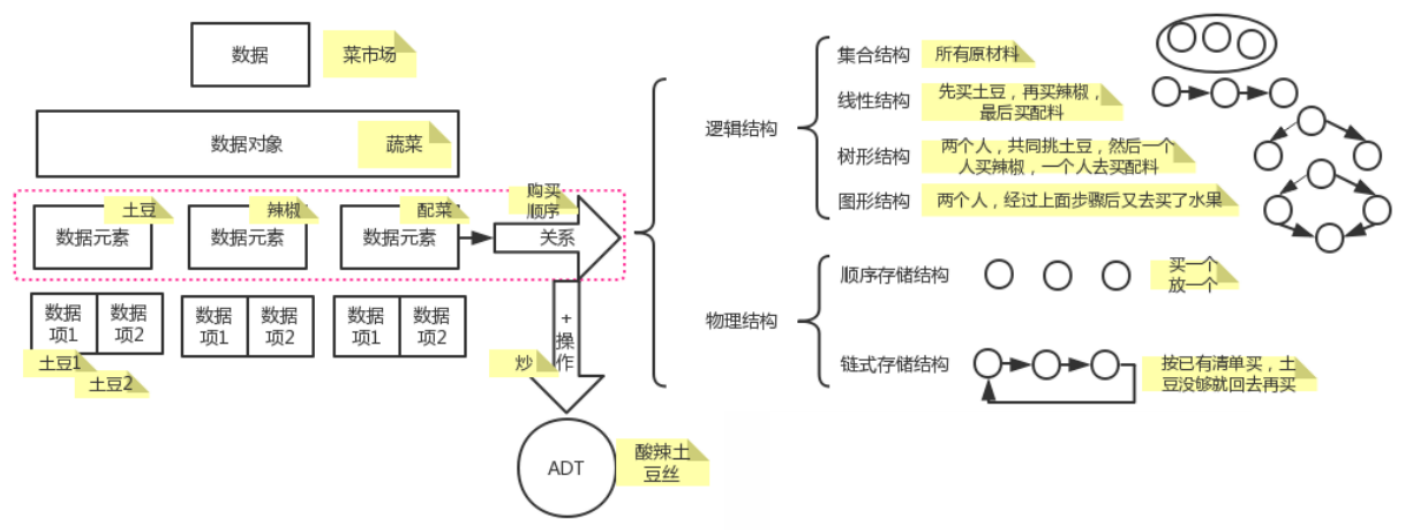
首先需要准备土豆、辣椒、配菜等原材料,这些原材料就是数据元素
之后我们需要存储这些数据,先选择逻辑结构,使用集合、线性、树形、图形哪种结构更适合
再选择物理结构,使用顺序或链式哪种存储方式更合理
当一切准备就绪后,进入算法环节: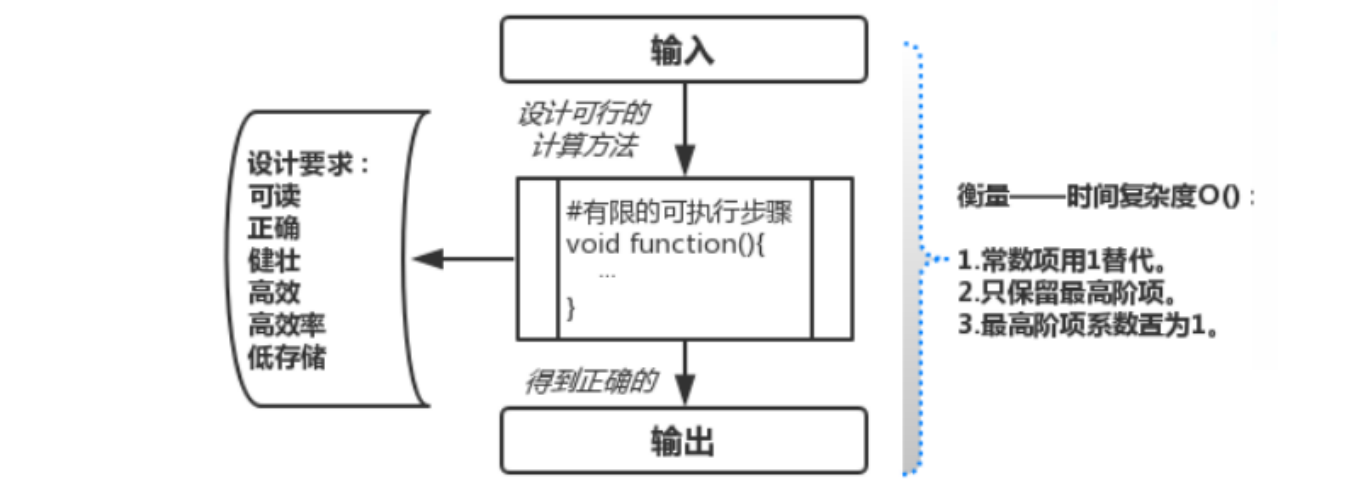
算法的特性:一定会有输入和输出,同时具备有穷性、确定性、可行性
算法有它的设计要求,可以体现在正确性、可读性、健壮性、时间效率和存储量等方面
2.2 算法的特性与设计要求
2.2.1 算法特性
有穷性:一个算法不能是无限循环的
确定性:一个算法需要有一个确定的输出结果
可行性:算法中的每一行指令都是可执行的
2.2.2 设计要求
正确性:衡量一个算法,首先要看它的输出结果是否正确
可读性:并不是代码越少越优秀
健壮性:一个算法不能因为错误的输入就导致程序挂掉,应当有一些适当的提示
时间效率高和存储量低:有部分算法会采用空间换取时间,但并不是绝对的。很多算法在相同的空间复杂度上,时间效率也能得到很大的提升
2.2.3 算法比较
案例:设计一个求得1 + 2 + 3 + ... + 100结果的程序
算法1:
int main(int argc, const char * argv[]) {int sum = 0;int n = 100;for(int i = 0; i <= n; i++){sum += i;}printf("%d", sum);return 0;}
算法2:
int main(int argc, const char * argv[]) {int sum = 0;int n = 100;sum = (1 + n) * n / 2;printf("%d", sum);return 0;}
- 算法2使用等差公式的特性,时间复杂度更低
2.3 时间复杂度
时间复杂度:它定性描述该算法的运行时间,常用大O符号表述。使用这种方式时,时间复杂度可被称为是渐近的,亦即考察输入值大小趋近无穷时的情况
大O表示法:
用常数
1取代运行时间中所有常数:3 → O(1)在修改运行次数函数中,只保留最高阶项:
n ^ 3 + 2n ^ 2 + 5→ O(n^3)如果在最高阶存在且不等于
1,则去除这个项目相乘的常数:2n ^ 3→ O(n^3)
时间复杂度术语:
常数阶
线性阶
对数阶
平方阶
立方阶
nlog阶指数阶(不考虑),例如:O(2^n)或者O(n!),除非是非常小的n,否则会造成噩梦般的时间消耗。这是一种不切实际的算法时间复杂度,一般不考虑
2.3.1 常数阶
常数阶时间复杂度计算:O(1)
void testSum1(int n){int sum = 0; //执行1次sum = (1 + n) * n / 2; //执行1次printf("testSum1:%d\n",sum); //执行1次}void testSum2(int n){int sum = 0; //执行1次sum = (1 + n) * n / 2; //执行1次sum = (1 + n) * n / 2; //执行1次sum = (1 + n) * n / 2; //执行1次sum = (1 + n) * n / 2; //执行1次sum = (1 + n) * n / 2; //执行1次printf("testSum2:%d\n",sum); //执行1次}void add(int x){x = x + 1; //执行1次}
testSum1:1 + 1 + 1=3→ O(1)testSum2:1 + 1 + 1 + 1 + 1 + 1 + 1=7→ O(1)add:1 → O(1)
无论n如何变化,代码的执行次数不会发生改变,所以三个案例的时间复杂度都是O(1)
2.3.2 线性阶
线性阶时间复杂度:O(n)
void testSum3(int n){int i,sum = 0; //执行1次for (i = 1; i <= n; i++) { //执行n+1次sum += i; //执行n次}printf("testSum3:%d\n",sum); //执行1次}
1 + (n + 1) + n + 1=3 + 2n→ O(n)
n的改变会导致代码执行次数的线性增长,所以案例中时间复杂度为O(n)
2.3.3 对数阶
对数阶时间复杂度:O(logn)
void testA(int n){
int count = 1; //执行1次
while (count < n) {
count = count * 2;
}
}
- x = log2n → O(log n)
当2的x次方等于n的时候,循环停止。所以案例中时间复杂度为O(log n)
2.3.4 平方阶
平方阶时间复杂度:O(n^2)
void testSum4(int n){
int sum = 0;
for(int i = 0; i < n;i++) {
for (int j = i; j < n; j++) {
sum += j;
}
}
printf("textSum4:%d",sum);
}
void testSum5(int n){
int i,j,x=0,sum = 0; //执行1次
for (i = 1; i <= n; i++) { //执行n+1次
for (j = 1; j <= n; j++) { //执行n(n+1)
x++; //执行n*n次
sum = sum + x; //执行n*n次
}
}
printf("testSum5:%d\n",sum); //执行1次
}
testSum4:j的循环次数依赖于i,当n = 0时,j循环n次。n = 1时,j循环n - 1次。n = 2时,j循环n - 2次…它符合等差数列的规则,故此可以使用公式:
sn = n(a1 + an) / 2n + (n - 1) + (n - 2) + ... + 1=n(n - 1) / 2=n ^ 2 / 2 + n / 2→ O(n^2)
testSum5:1 + (n + 1) + n(n + 1) + n ^ 2 + n ^ 2 + 1=2 + 2 + 3n ^ 2 + 2n→ O(n^2)
2.3.5 立方阶
立方阶时间复杂度:O(n^3)
void testB(int n){
int sum = 1; //执行1次
for (int i = 0; i < n; i++) { //执行n次
for (int j = 0 ; j < n; j++) { //执行n*n次
for (int k = 0; k < n; k++) { //执行n*n*n次
sum = sum * 2; //执行n*n*n次
}
}
}
}
1 + n + n * n + n * n * n + n * n * n=1 + n + n ^ 2 + n ^ 3 * 2→ O(n^3)
2.3.6 示例分析
示例:
| 执行次数函数 | 阶 | 术语 |
|---|---|---|
| 12 | O(1) | 常数阶 |
| 2n + 3 | O(n) | 线性阶 |
| 3n ^ 2 + 2n + 1 | O(n^2) | 平方阶 |
| 5log2n + 20 | O(log n) | 对数阶 |
| 2n + 3nlog2n + 19 | O(nlog n) | nlog阶 |
| 6n ^ 3 + 2n ^ 2 + 3n + 4 | O(n^3) | 立方阶 |
| 2 ^ n | O(2^n) | 线性阶 |
时间复杂度由低到高排序:
O(1) < O(log n) < O(n) < O(nlog n) < O(n^2) < O(n^3) < O(2^n) < O(n!) < O(n ^ n)
2.4 空间复杂度
空间复杂度:通过计算算法所需的存储空间实现,算法空间复杂度的计算公式:S(n) = n(f(n)),其中n为问题的规模,f(n)为语句关于n所占存储空间的函数
考量算法的空间复杂度,主要考虑算法执行时所需要的辅助空间
案例:数组逆序,将一维数组a中的n个数逆序存放在原数组中
算法1:
int main(int argc, const char * argv[]) {
//输入,不算辅助空间
int n = 5;
int a[10] = {1,2,3,4,5,6,7,8,9,10};
//算法实现
int temp;
for(int i = 0; i < n/2 ; i++){
temp = a[i];
a[i] = a[n-i-1];
a[n-i-1] = temp;
}
for(int i = 0;i < 10;i++)
{
printf("%d\n",a[i]);
}
return 0;
}
- 只使用一个临时变量,空间复杂度:O(1)
算法2:
int main(int argc, const char * argv[]) {
//输入,不算辅助空间
int n = 5;
int a[10] = {1,2,3,4,5,6,7,8,9,10};
//算法实现
int b[10] = {0};
for(int i = 0; i < n;i++){
b[i] = a[n-i-1];
}
for(int i = 0; i < n; i++){
a[i] = b[i];
}
for(int i = 0;i < 10;i++)
{
printf("%d\n",a[i]);
}
return 0;
}
- 算法使用了
b[10]的数组,空间复杂度:O(n)
2.5 效率衡量方法
一个算法有最好的情况与最坏的情况,在衡量一个算法的时候,特别是时间复杂度,我们会优先衡量最坏的情况,其次衡量算法的平均情况
例如:
假设寻找
n = 6,循环在第一次就可以找到它的位置假设寻找
n = 1,寻找在第十次就可以找到它的位置
衡量算法时,我们使用的大O表示法,衡量的就是算法的最坏情况,也就是底线
日常我们设计算法时,针对同一需求实现的多种算法,时间复杂度可能都是O(n)。在最坏情况相同的时候,接下来可以衡量算法的平均情况
3. 线性表
线性表是一对一的逻辑结构,对于非空的线性表和线性结构,其特点如下:
存在唯一的一个被称作“第一个”的数据元素
存在唯一的一个被称作“最后一个”的数据元素
除了第一个之外,结构中的每个数据元素均有一个前驱
除了最后一个之外,结构中的每个数据元素都有一个后继
线性表常见的方法:
ADT List {
Data:线性表的数据对象集合为{a1, a2, ..., an},每个元素的类型均为DataType。其中,除了第一个元素a1之外,每个元素都且只有一个直接前驱元素,除了最后一个元素an之外,每个元素有且只有一个直接后继元素。数据元素之间的关系是一对一的关系
Operation
InitList(&L);
操作结果:初始化操作,建立一个空的线性表L
DestroyList(&L);
初始条件:线性表L已存在
操作结果:销毁线性表L
ClearList(&L);
初始条件:线性表L已存在
操作结果:将L重置为空表
ListLength(L);
初始条件:线性表L已存在
操作结果:返回L中数据元素的个数
GetElem(L, i, &e);
初始条件:线性表L已存在,且1<=i<ListLength(L)
操作结果:用e返回L中第i个数据元素的值
LocateElem(L, e);
初始条件:线性表L已存在
操作结果:返回L中第一个值与e相同的元素在L中的位置,若数据不存在,则返回0
PriorElem(L, cur_e, &pre_e);
初始条件:线性表L已存在
操作结果:若cur_e是L的数据元素,且不是第一个,则用pre_e返回其前驱,否则操作失败
NextElem(L, cur_e, &next_e);
初始条件:线性表L已存在
操作结果:若cur_e是L的数据元素,且不是最后一个,则用next_e返回其后继,否则操作失败
ListInsetr(L, i, e);
初始条件:线性表L已存在,且1<=i<=ListLength(L)
操作结果:在L中第一个位置之前插入新的数据元素e,L长度+1
ListDelete(L, i);
初始条件:线性表L已存在,且i<=i<=ListLength(L)
操作结果:删除L的第i个元素,L长度-1
TraverseList(L);
初始结果:线性表L已存在
操作结果:对线性表L进行遍历,在遍历的过程中对L的每个结点访问1次
}
3.1 顺序存储
线性表的顺序存储,逻辑相邻,物理存储地址也相邻
3.1.1 初始化 & 基础功能
let OK : Int = 1;
let ERROR : Int = 0;
struct LinearList<Element: Equatable> {
fileprivate var _data : UnsafeMutablePointer<Element?>;
fileprivate var _length : Int;
fileprivate var _capacity : Int;
init(size : Int) {
_length = 0;
_capacity = size + 1;
_data = UnsafeMutablePointer.allocate(capacity: _capacity);
_data.initialize(repeating: nil, count: _capacity);
}
mutating func destroy() {
_data.deinitialize(count: _capacity);
_data.deallocate();
_length = 0;
_capacity = 0;
}
mutating func clear() {
_length = 0;
}
func length() -> Int {
return _length;
}
fileprivate func capacity() -> Int {
return length() + 1;
}
};
- 开辟空间
+1,元素从第一位开始存储。预留第零位作为哨兵,之后的一些逻辑中会使用
3.1.2 获取元素 & 位置查找
struct LinearList<Element: Equatable> {
func getElem(locate : Int) -> Element? {
if(locate < 1 || locate > length()){
return nil;
}
return _data[locate];
}
func getLocate(element : Element) -> Int {
if(length() < 1){
return 0;
}
var locate = 0;
for index in 1...length(){
let val = getElem(locate: index)!;
if(val == element){
locate = index;
break;
}
}
return locate;
}
};
3.1.3 获取前驱与后继
struct LinearList<Element: Equatable> {
func getPriorElem(element : Element) -> Element? {
let locate = getLocate(element: element)
if(locate < 2){
return nil;
}
let val = getElem(locate: locate - 1);
return val;
}
func getNextElem(element : Element) -> Element? {
let locate = getLocate(element: element)
if(locate >= length()){
return nil;
}
let val = getElem(locate: locate + 1);
return val;
}
};
3.1.4 插入与删除
struct LinearList<Element: Equatable> {
mutating func insetr(locate : Int, element : Element) -> Int {
if(locate < 1 || locate > capacity() || capacity() == _capacity){
return ERROR;
}
if(locate < capacity()){
for i in (locate..<capacity()).reversed(){
let val = getElem(locate: i)!;
_data.advanced(by: i + 1).pointee = val;
}
}
_data.advanced(by: locate).pointee = element;
_length += 1;
return OK;
}
mutating func delete(locate : Int) -> Int {
if(locate < 1 || locate > length()){
return ERROR;
}
if(locate < length()){
for i in locate..<length(){
let val = getElem(locate: i + 1)!;
_data.advanced(by: i).pointee = val;
}
}
_length -= 1;
return OK;
}
};
- 结构体初始化时,已经分配
data空间的大小。所以删除元素时,只更新长度,不需要处理该元素
3.1.5 遍历打印
struct LinearList<Element: Equatable> {
func traverse() -> String {
var str : String = "";
if(length() == 0){
return str;
}
for i in 1...length(){
let val = getElem(locate: i)!;
str += "\(val),"
}
return str;
}
};
3.2 链式存储
线性表的链式存储,逻辑相邻,物理存储地址不连续
单链表结点分为数据域和指针域
- 链式存储最大的特定是内存不连续,所以数据之间依赖指针进行连接
单链表的逻辑状态: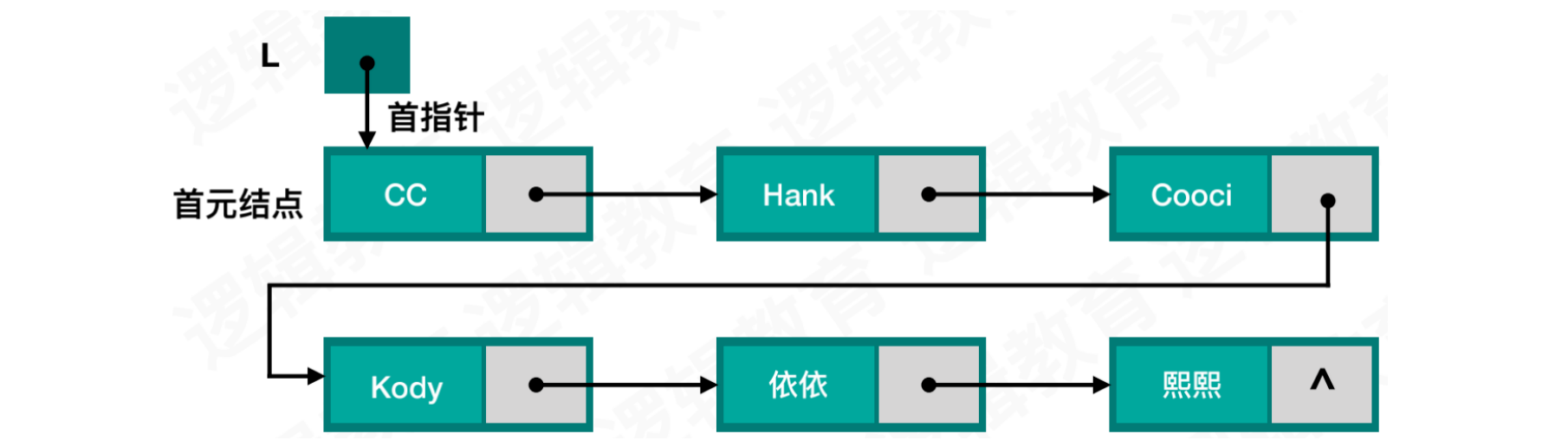
链表中第一个结点称之为首元结点
最后一个结点的特点是指针为空
为了单链表在插入和删除时更加方便,我们可以为单链表增加一个头结点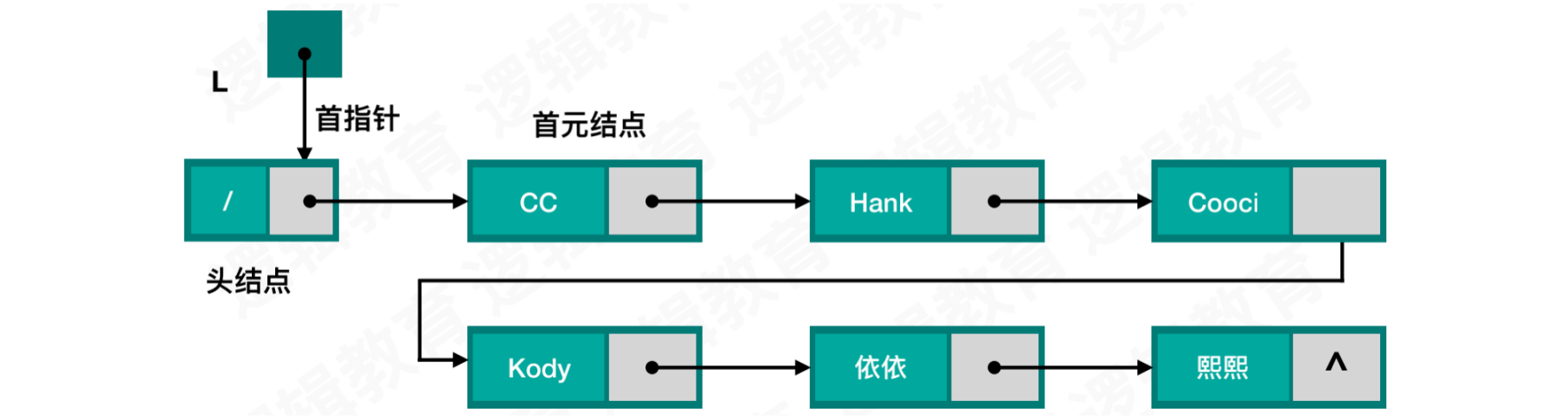
首指针指向头结点,头结点的指针指向首元结点
头结点的作用:
便于对首元结点的操作,例如:首元结点的插入和删除
便于空表和非空表的统一处理
头结点相当于一个标志,不需要存储数据,仅使用它的指针
头结点的数据也可存储链表长度或其他辅助信息
空表结构:
非空表结构: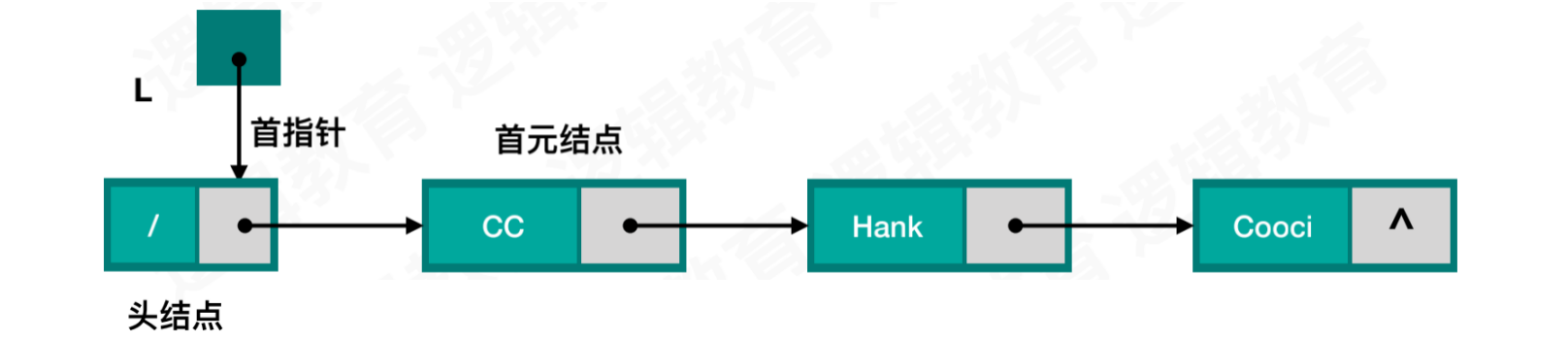
3.2.1 数据结构
public struct LinkedList<Element>{
fileprivate class Node<T> {
var next : Node<T>?;
var data : T?;
init(){
}
init(data : T){
self.data = data;
self.next = nil;
}
deinit {
print("值为\(data!)的Node释放");
}
}
fileprivate var _head : Node<Element>? = nil;
private var _length : Int = 0;
public init(){
_head = Node<Element>();
}
func length() -> Int {
return _length;
}
fileprivate func capacity() -> Int {
return length() + 1;
}
}
3.2.2 获取查找
public struct LinkedList<Element>{
func getElem(locate : Int) -> Element? {
if(locate < 1 || locate > length()){
return nil;
}
let node = getNode(index: locate);
if(node == nil){
return nil;
}
return node!.data;
}
fileprivate func getNode(index : Int) -> Node<Element>? {
if(index < 0 || index > length()){
return nil;
}
var i = 0;
var node = _head;
while(node != nil && i < index){
node = node?.next;
i += 1;
}
return node;
}
}
3.2.3 插入与删除
单链表插入:在单链表的两个数据元素a和b之间,插入一个数据元素s。已知p为其单链表存储结构中指向结点a的指针
插入结点之前:
插入结点之后: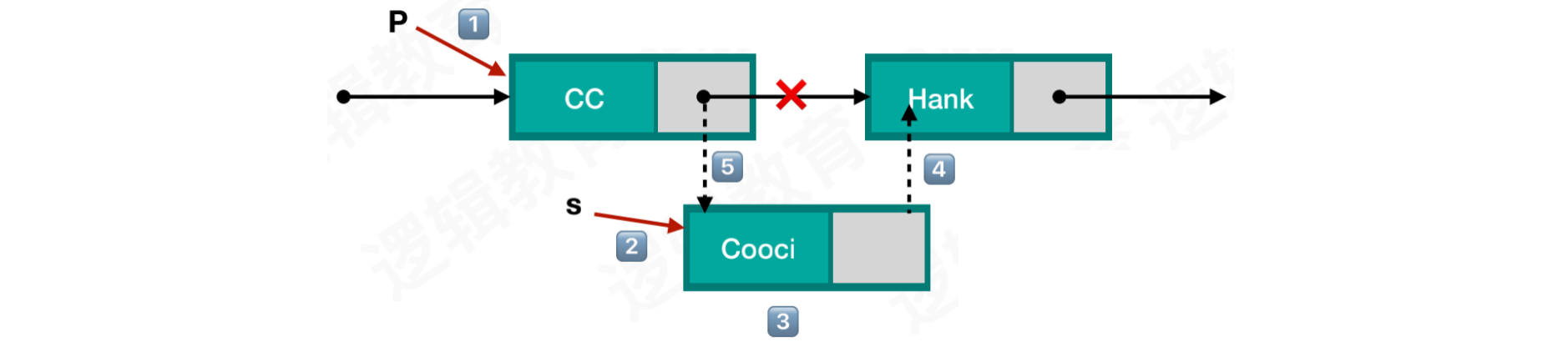
通过指针
p遍历链表,找到a结点创建即将插入的
s结点,进行数据域的赋值,指针域指向b结点将
a结点的指针域指向s结点
单链表删除:删除单链表中指定位置的元素,同插入元素一样。找到该位置的前驱结点,将前驱结点的指针域指向待删除结点的后继结点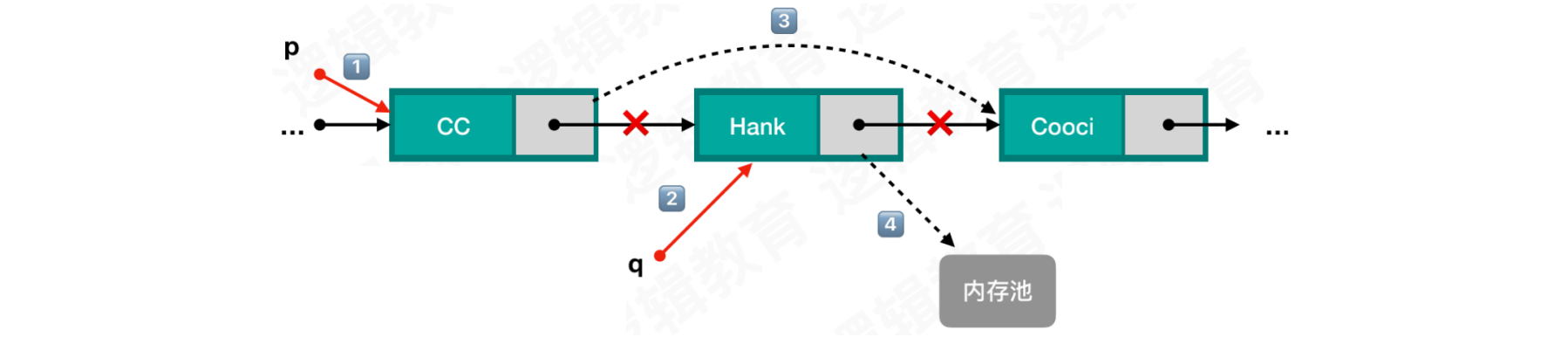
通过指针
p遍历链表,找到待删除结点的前驱结点创建指针
q,指向待删除结点将前驱结点的指针域,指向待删除结点的后继结点
销毁被删除的结点
单链表的插入与删除:
public struct LinkedList<Element>{
mutating func insetr(locate : Int, element : Element) -> Int {
if(locate < 1 || locate > capacity()){
return ERROR;
}
let node = Node<Element>(data: element);
return insetrNode(locate: locate, node: node);
}
fileprivate mutating func insetrNode(locate : Int, node : Node<Element>) -> Int {
let index = locate - 1;
let ptr = getNode(index: index);
node.next = ptr?.next;
ptr?.next = node;
_length += 1;
return OK;
}
mutating func delete(locate : Int) -> Element? {
if(locate < 1 || locate > length()){
return nil;
}
let node = getNode(index: locate);
if(node == nil){
return nil;
}
let preNode = getNode(index: locate - 1);
let nextNode = getNode(index: locate + 1);
preNode?.next = nextNode;
_length -= 1;
return node?.data;
}
}
3.2.4 前插法与后插法
使用前插法创建单链表,假设插入随机数: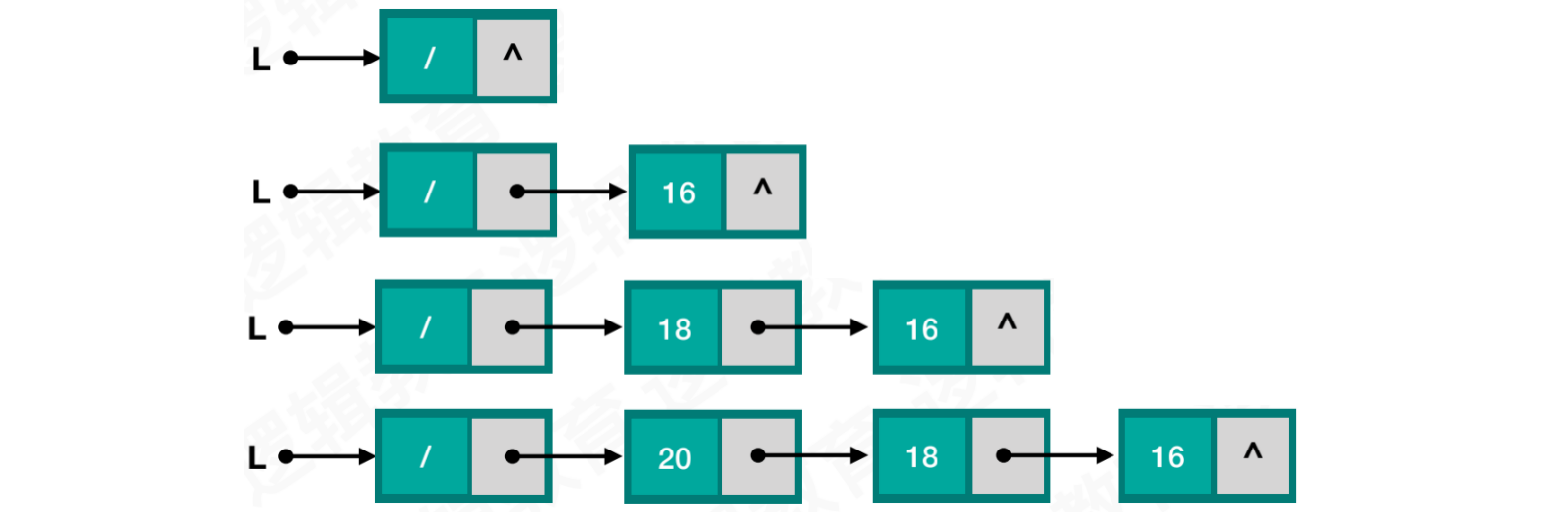
- 新数据永远插入到头结点之后
使用后插法创建单链表,假设插入随机数: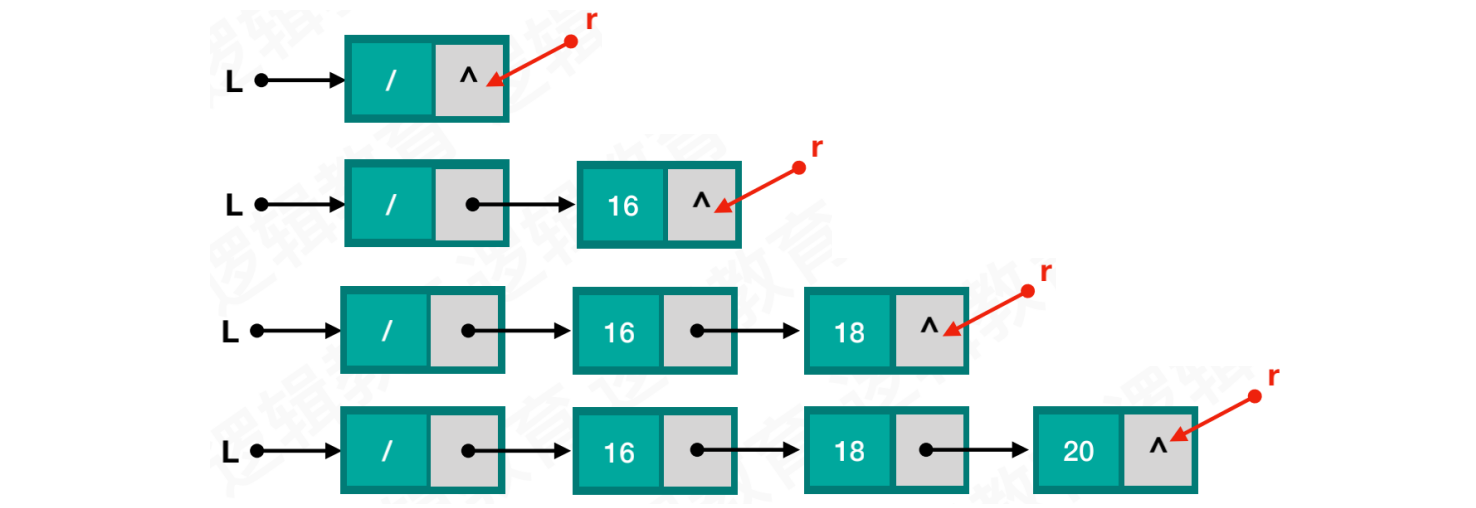
- 使用指针
r指向尾结点,每次插入新数据都在尾结点之后
单链表的前插法与后插法:
public struct LinkedList<Element>{
fileprivate var _r : Node<Element>? = nil;
public init(){
_head = Node<Element>();
_r = _head;
}
mutating func pushHead(element : Element) -> Int{
let node = Node<Element>(data: element);
node.next = _head?.next;
_head?.next = node;
if(length() == 0){
_r = node;
}
_length += 1;
return OK;
}
mutating func pushTail(element : Element) -> Int{
let node = Node<Element>(data: element);
_r?.next = node;
_r = node;
_r?.next = nil;
_length += 1;
return OK;
}
}
3.3 顺序与链式的优缺点
存储分配方式:
顺序存储结构用一段连续的存储单元,依次存储线性表的数据元素
单链表采用链式存储结构,用一组任意的存储单元存放线性表的元素
时间性能:
查找
顺序存储:O(1)
单链表:O(n)
插入与删除
存储结构需要平均一个表长一半的元素,时间O(n)
单链表查找某位置后的指针后,插入和删除为O(1)
空间性能
顺序存储结构需要预先分配存储空间,分太大,浪费空间。分太小,发生溢出
单链表不需要分配存储空间,只要有就可以分配,元素个数也不受限制
总结
数据结构:
- 指的数据对象中的数据元素之间的关系
基本数据单位:
数据:程序的操作对象,用于描述客观事务
可以输入到计算机
可以被计算机处理
数据对象:性质相同的数据元素的集合,类似于数组
数据元素:组成数据对象的基本单位
数据项:一个数据元素由若干数据项组成
存储结构:
数据元素之间不是独立的,存在特定的关系,这些关系即是结构
分析数据结构时,一般有两种视角:逻辑结构和物理结构
逻辑结构:描述数据与数据之间的逻辑关系
集合结构:所有数据都属于同一集合,元素之间平等,没有顺序。例如:
OC中的NSSet线性结构:数据之间是一对一的关系。例如,线性表、数组、队列、栈、字符串等
其中队列和栈属于特殊的线性结构,因为满足数据一对一关系。它们的特殊在于读取方式,队列为先进先出,栈为先进后出
字符串也属于特殊的线性结构,它由
N个字符组成,满足数据一对一关系。它的特殊在于只能存储字符串
树形结构:数据之间是一对多的关系。例如:二叉树、B树、多路树、红黑树、平衡二叉树等
图形结构:数据之间多对多的结构。例如:邻接矩阵、邻接表
物理结构:数据存储在磁盘中的方式
顺序存储结构:
特定:开辟一段连续的内存空间,数据依次存储。例如:数组
缺陷:当插入、删除元素时,除了操作指定位置的元素之外,还要将后面的元素移动位置
链式存储结构:
特定:不需要提前开辟连续空间。例如:链表
缺陷:查找元素时需要进行遍历操作
算法:
指解决特定问题求解步骤的描述。在计算机中表现为指令的有限序列,并且每个指令表示一个或多个操作
数据结构与算法二者是不可分割的
算法特性:
有穷性:一个算法不能是无限循环的
确定性:一个算法需要有一个确定的输出结果
可行性:算法中的每一行指令都是可执行的
设计要求:
正确性:衡量一个算法,首先要看它的输出结果是否正确
可读性:并不是代码越少越优秀
健壮性:一个算法不能因为错误的输入就导致程序挂掉,应当有一些适当的提示
时间效率高和存储量低:有部分算法会采用空间换取时间,但并不是绝对的。很多算法在相同的空间复杂度上,时间效率也能得到很大的提升
时间复杂度:
时间复杂度:它定性描述该算法的运行时间,常用大O符号表述。使用这种方式时,时间复杂度可被称为是渐近的,亦即考察输入值大小趋近无穷时的情况
大O表示法:
用常数1取代运行时间中所有常数:3 → O(1)
在修改运行次数函数中,只保留最高阶项:n ^ 3 + 2n ^ 2 + 5 → O(n^3)
如果在最高阶存在且不等于1,则去除这个项目相乘的常数:2n ^ 3 → O(n^3)
时间复杂度术语:
常数阶:O(1)
线性阶:O(n)
对数阶:O(log n)
平方阶:O(n^2)
立方阶:O(n^3)
nlog阶:O(nlog n)
指数阶(不考虑),例如:O(2^n)或者O(n!),除非是非常小的n,否则会造成噩梦般的时间消耗。这是一种不切实际的算法时间复杂度,一般不考虑
时间复杂度由低到高排序:
- O(1) < O(log n) < O(n) < O(nlog n) < O(n^2) < O(n^3) < O(2^n) < O(n!) < O(n ^ n)
空间复杂度:
通过计算算法所需的存储空间实现,算法空间复杂度的计算公式:S(n) = n(f(n)),其中n为问题的规模,f(n)为语句关于n所占存储空间的函数
考量算法的空间复杂度,主要考虑算法执行时所需要的辅助空间
效率衡量方法:
- 一个算法有最好的情况与最坏的情况,在衡量一个算法的时候,特别是时间复杂度,我们会优先衡量最坏的情况,其次衡量算法的平均情况
线性表:
线性表是一对一的逻辑结构,对于非空的线性表和线性结构,其特点如下:
存在唯一的一个被称作“第一个”的数据元素
存在唯一的一个被称作“最后一个”的数据元素
除了第一个之外,结构中的每个数据元素均有一个前驱
除了最后一个之外,结构中的每个数据元素都有一个后继
线性表的顺序存储,逻辑相邻,物理存储地址也相邻
- 开辟连续的内存空间,删除元素时,只更新长度,不需要处理该元素
线性表的链式存储,逻辑相邻,物理存储地址不连续
单链表:
单链表结点分为数据域和指针域
链式存储最大的特定是内存不连续,所以数据之间依赖指针进行连接
链表中第一个结点称之为首元结点
最后一个结点的特点是指针为空
为了单链表在插入和删除时更加方便,我们可以为单链表增加一个头结点
首指针指向头结点,头结点的指针指向首页结点
头结点的作用:
便于对首元结点的操作,例如:首元结点的插入和删除
便于空表和非空表的统一处理
头结点相当于一个标志,不需要存储数据,仅使用它的指针
头结点的数据也可存储链表长度或其他辅助信息
单链表插入:
通过指针
p遍历链表,找到a结点创建即将插入的
s结点,进行数据域的赋值,指针域指向b结点将
a结点的指针域指向s结点
单链表删除:
通过指针
p遍历链表,找到待删除结点的前驱结点创建指针
q,指向待删除结点将前驱结点的指针域,指向待删除结点的后继结点
销毁被删除的结点
前插法与后插法:
前插法:新数据永远插入到头结点之后
后插法:使用指针
r指向尾结点,每次插入新数据都在尾结点之后
顺序与链式的优缺点:
存储分配方式:
顺序存储结构用一段连续的存储单元,依次存储线性表的数据元素
单链表采用链式存储结构,用一组任意的存储单元存放线性表的元素
时间性能:
查找
顺序存储:O(1)
单链表:O(n)
插入与删除
存储结构需要平均一个表长一半的元素,时间O(n)
单链表查找某位置后的指针后,插入和删除为O(1)
空间性能
顺序存储结构需要预先分配存储空间,分太大,浪费空间。分太小,发生溢出
单链表不需要分配存储空间,只要有就可以分配,元素个数也不受限制

