1. 概述

KMP算法是一种改进的字符串匹配算法，由D.E.Knuth、J.H.Morris和V.R.Pratt提出，简称KMP算法

KMP算法的核心是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。本质是通过一个next数组，里面包含了模式串的局部匹配信息，找到模式串中各位置最适合的回溯位置

KMP算法的时间复杂度为O(m + n)

2. 匹配规则

例如：查找出模式串在主串第⼀次出现的位置

2.1 情况一

主串：S = "abcdefgab"，模式串T = "abcdex"

如果使用BF算法，主串和模式串的前五次匹配都一致，直到第六次匹配时字符出现差异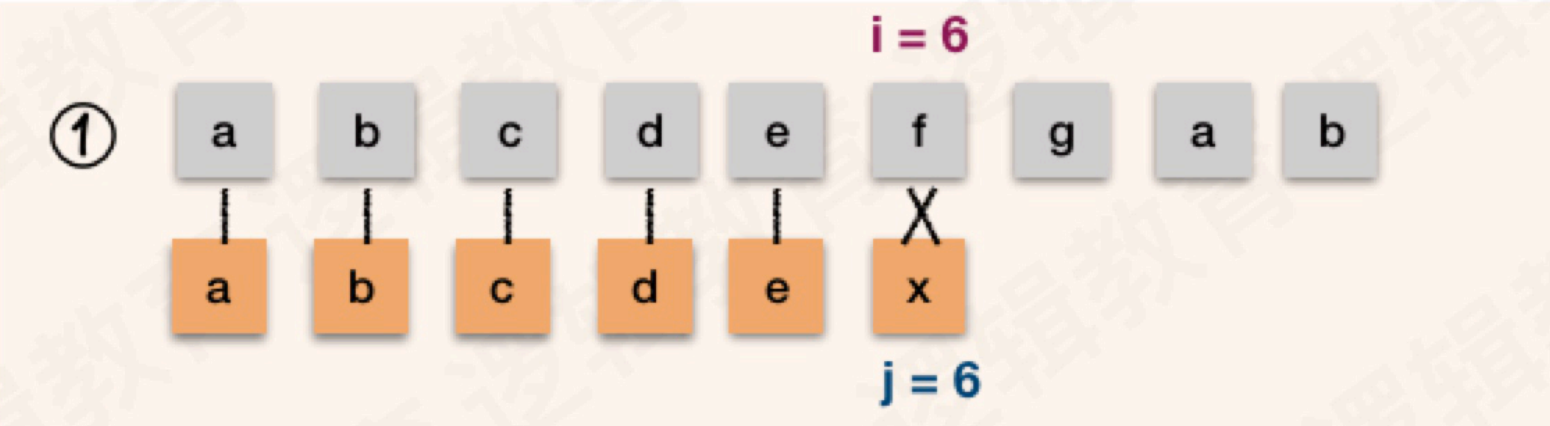
image.png

  • 此时主串中i的位置为6，模式串中j的位置也为6

按照BF算法的逻辑，接下来将主串i位置移动到2，模式串j位置移动到1，向后依次匹配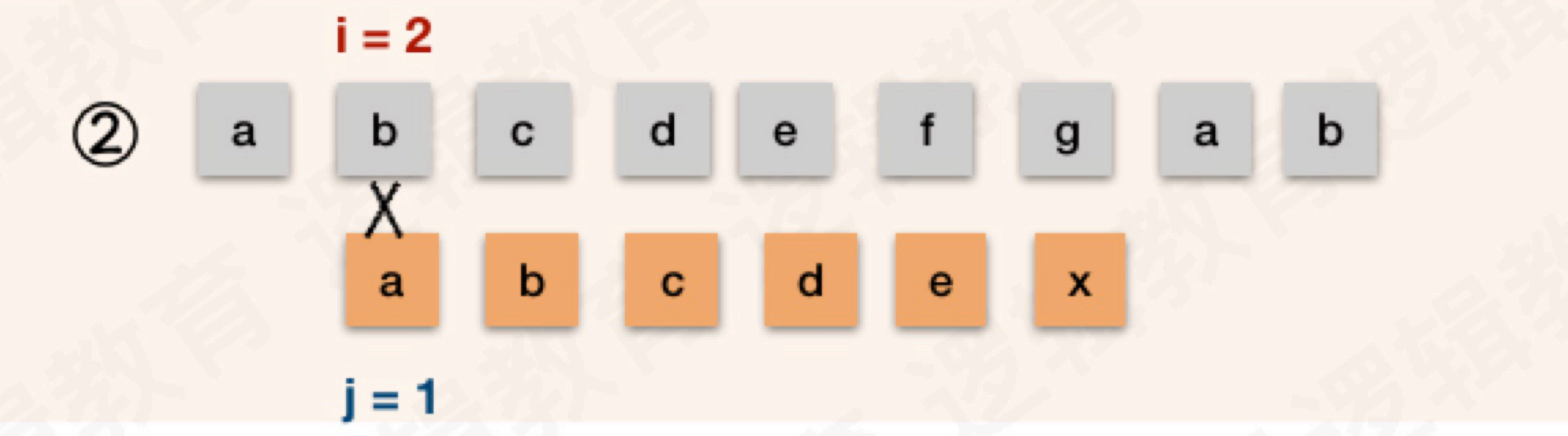
image.png

如果不能完全匹配，主串继续i + 1，而模式串j永远回到1的位置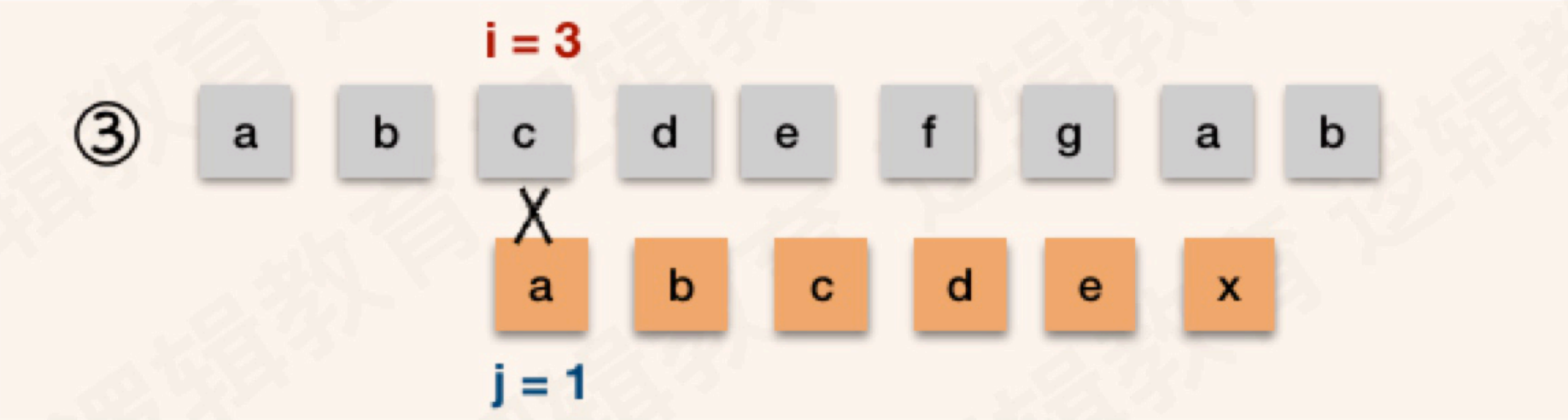
image.png

主串中的4、5、6...及后续字符，都会循环这个匹配流程，直到完全命中或主串匹配结束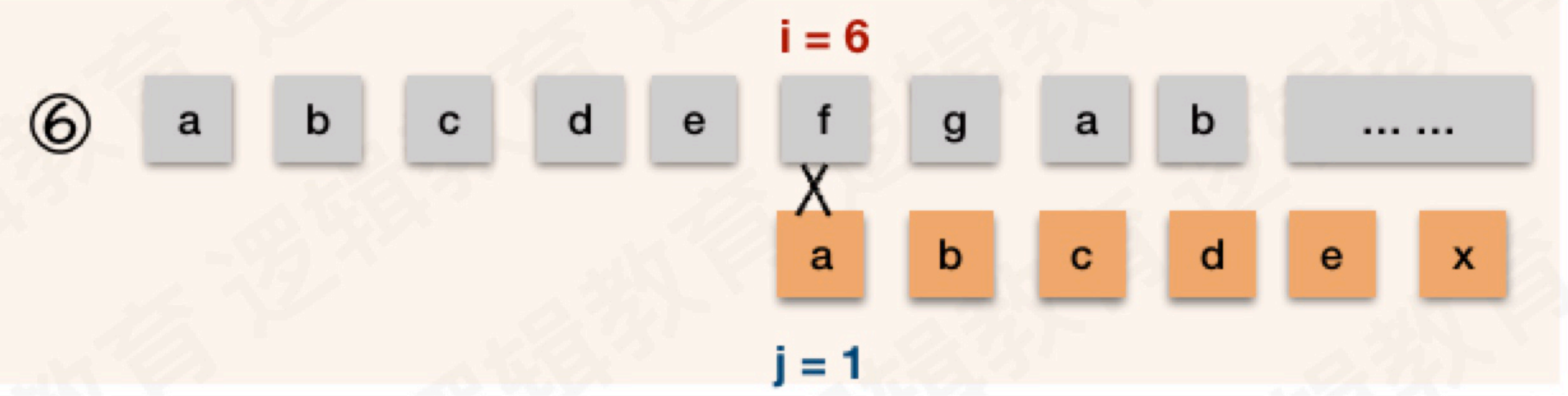
image.png

我们仔细观察模式串，发现它的首字符a和后面的bcdex各不相等。但在流程一匹配时，主串和模式串中前五个字符全部匹配成功

这意味着模式串中的a字符和主串中2 ~ 5位置的字符一定无法匹配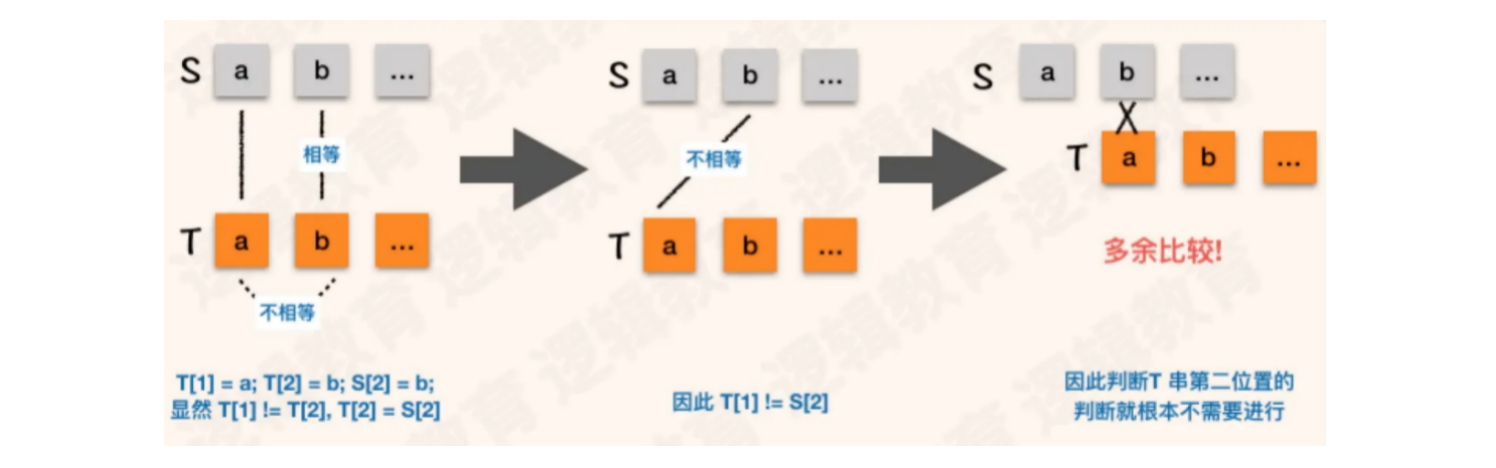
image.png

而BF算法中的第2 ~ 5次的匹配流程完全是多余的，我们完全可以在流程一匹配失败之后，直接进入流程六的匹配

之所以进入流程六的匹配，因为在流程一中得到了S[6] != T[6]的结论，但我们并不知道S[6]和T[1]是否可以匹配成功，所以流程六必须保留

2.2 情况二

主串：S = "abcababca"，模式串T = "abcabx"

第一次匹配，主串和模式串前五位字符一致，第六位匹配失败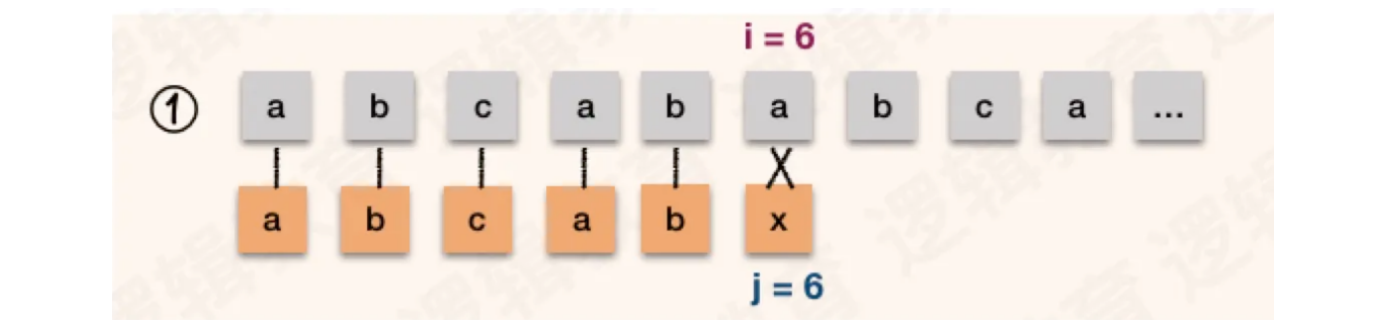
image.png

根据【情况一】的结论，模式串中首字符a和第2 ~ 3位的b、c不同，但主串和模式串中2 ~ 3位已经匹配，所以模式串可以跳过主串的第2~3位匹配，直接匹配主串的第四位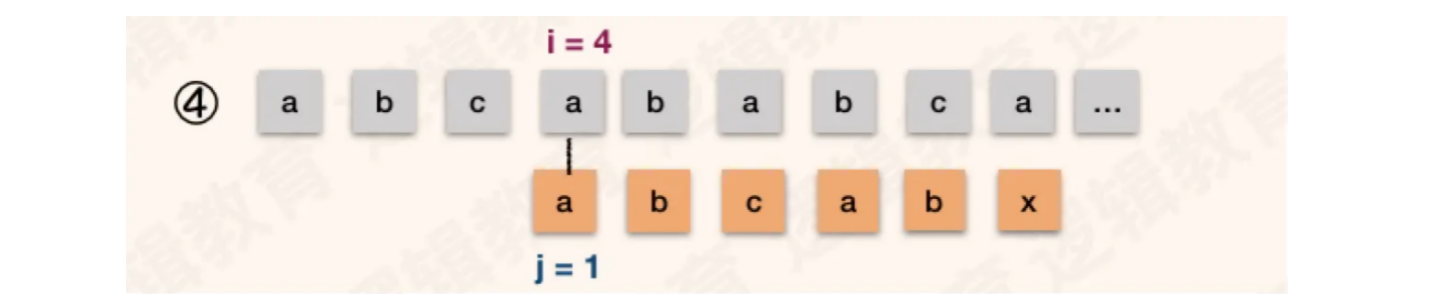
image.png

当S[4] == T[1]，继续后面字符的比较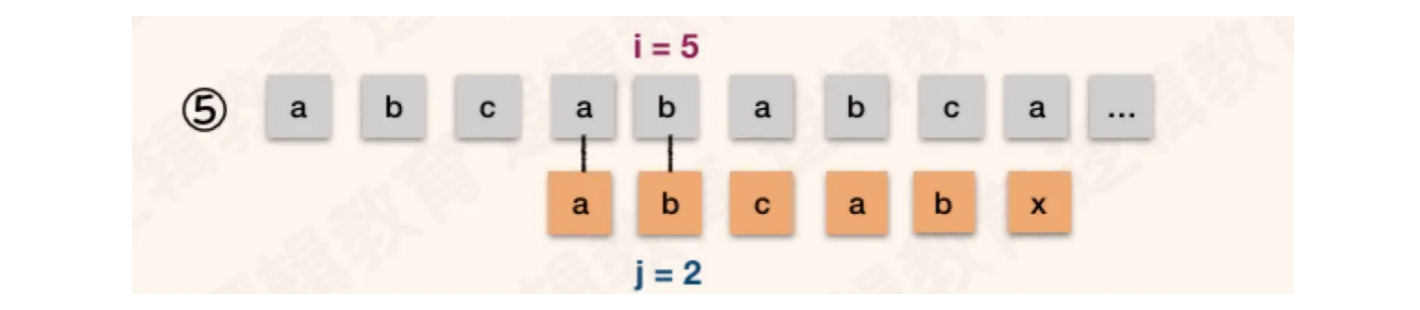
image.png

这种情况同样具备优化空间，从模式串中得知1 ~ 2为的ab和4 ~ 5位相同，而流程一中得知S[4] == T[4]且S[5] == T[5]，所有流程四和流程五的比对都是多余的

更优的方式，当流程一匹配失败后，应该直接进入S[6]和T[3]的匹配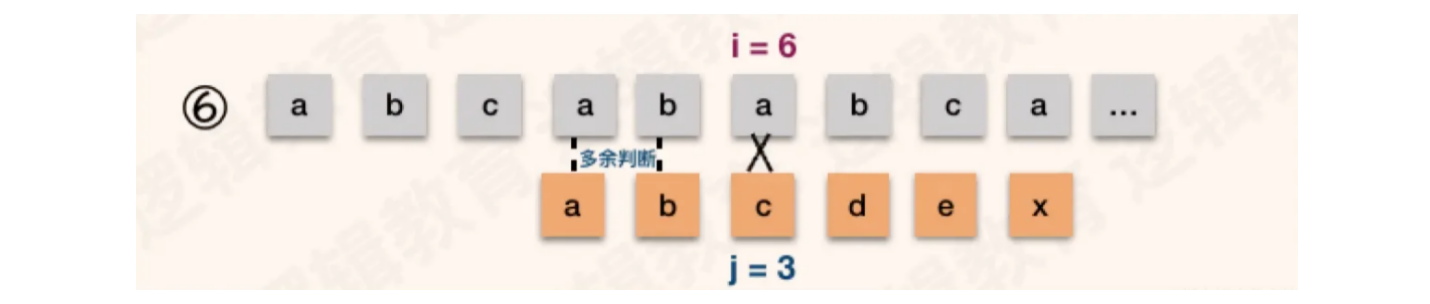
image.png

3. 算法特点

根据上述规则，不难看出KMP是在设法利用已知信息，避免将对比位置移回到已经对比过的位置上，而是将它向后移动继续对比，从而提高对比的效率

所以KMP算法的最大特点，就是避免了不必要的回溯发生

根据【情况一】的示例：

主串：S = "abcdefgab"，模式串T = "abcdex"

当第一次匹配结束后，i停留在位置6，按照KMP算法的特定，我们跳过不必要的匹配流程，下一轮的匹配i依然从位置6开始，它会和S[1]进行对比

由此可见，i的位置是不需要回溯的。在完整的匹配流程中，i的值也不可能变小

既然i不能回溯，在完整的匹配流程中，我们只能不停的改变j的位置。遇到匹配失败的时候，将j回溯到最优的位置，继续下一次的对比。而j的回溯位置，只会取决于模式串T的内容

4. next数组的推导

j值取决于当前字符之前的串前后缀的相似度，我们把模式串各个位置j值变化定义为一个next数组，那么next的长度就是模式串的长度

计算模式串T的next数组，其实就是在求解模式串的回溯位置

针对next[j]的函数定义：
image.png

我们可以通过以下几种情况，进一步对公式进行分析

4.1 模式串中无任何字符重复

示例：
image.png

  • j为模式串T中字符对应的位置，从1开始

  • 当j == 1时，next[1] = 0

  • 当j == 2时，T[1] ~ T[j - 1]中只有字符a，属于其他情况，next[2] = 1

  • 当j == 3时，T[1] ~ T[j - 1]中字符为ab。由于a != b，属于其他情况，next[3] = 1

  • 当j == 4时，T[1] ~ T[j - 1]中字符为abc。由于不包含相同的前后缀，属于其他情况，next[4] = 1

  • 当j == 5时，T[1] ~ T[j - 1]中字符为abcd。由于不包含相同的前后缀，属于其他情况，next[5] = 1

  • 当j == 6时，T[1] ~ T[j - 1]中字符为abcde。由于不包含相同的前后缀，属于其他情况，next[6] = 1

当模式串中无任何字符重复，在next数组推导过程中，只能命中公式图中的第一种情况和第三种情况，所以next数组 = [0, 1, 1, 1, 1, 1]

4.2 模式串中包含相同前后缀

示例：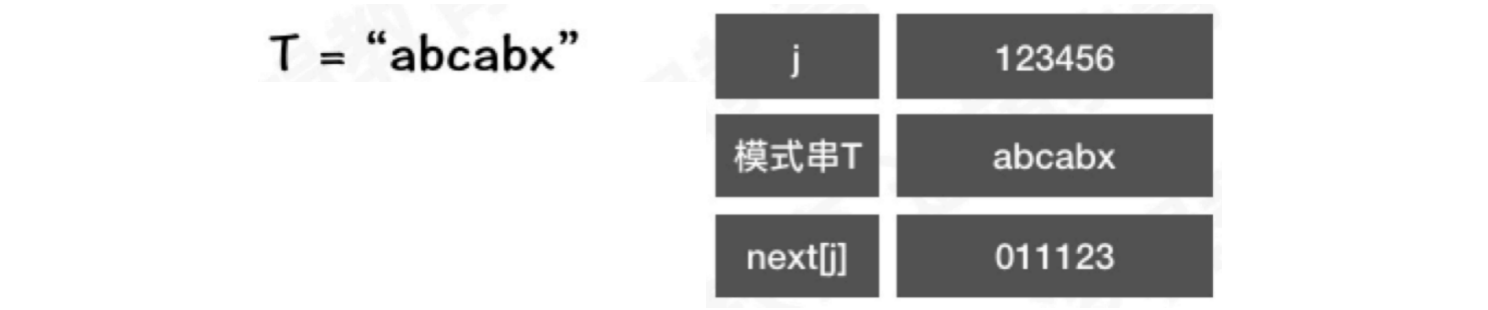
image.png

  • 当j == 1时，next[1] = 0

  • 当j == 2时，T[1] ~ T[j - 1]中只有字符a，属于其他情况，next[2] = 1

  • 当j == 3时，T[1] ~ T[j - 1]中字符为ab。由于a != b，属于其他情况，next[3] = 1

  • 当j == 4时，T[1] ~ T[j - 1]中字符为abc。由于不包含相同的前后缀，属于其他情况，next[4] = 1

  • 当j == 5时，T[1] ~ T[j - 1]中字符为abca。其中前缀a和后缀a相等，通过公式p[1] ~ p[k-1] = p[j - k - 1] ~ p[j - 1]可以推算出k = 2，因此next[5] = 2

  • 当j == 6时，T[1] ~ T[j - 1]中字符为abcab。其中前缀ab和后缀ab相等，通过公式可以推算出k = 3，因此next[6] = 3

k值的规则：当前后缀相等时，如果前后缀由一个字符组成，则k = 2。如果前后缀由两个字符组成，则k = 3。如果前后缀由N个字符组成，则k = N + 1

4.3 模式串类似于ababaaaba

示例：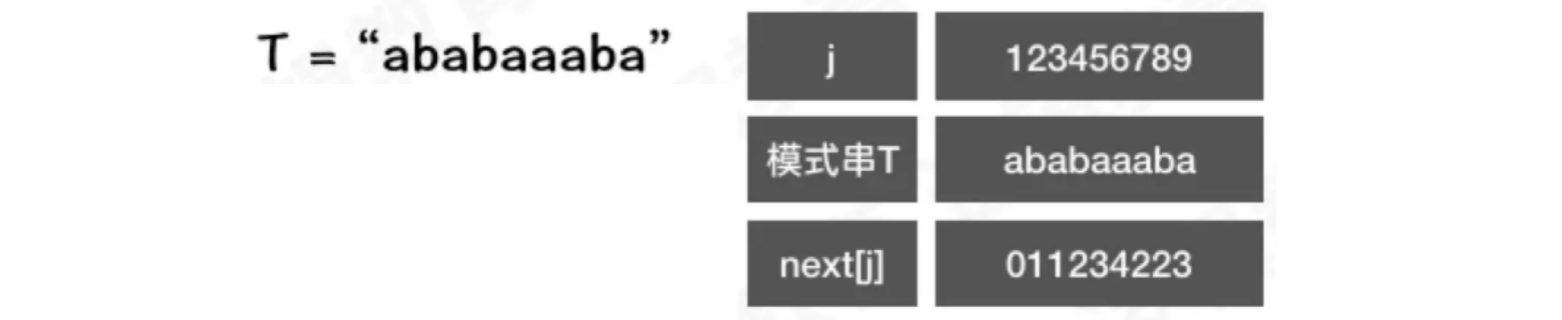
image.png

  • 当j == 1时，next[1] = 0

  • 当j == 2时，T[1] ~ T[j - 1]中只有字符a，属于其他情况，next[2] = 1

  • 当j == 3时，T[1] ~ T[j - 1]中字符为ab。由于a != b，属于其他情况，next[3] = 1

  • 当j == 4时，T[1] ~ T[j - 1]中字符为aba。其中前缀a和后缀a相等，通过公式可以推算出k = 2，因此next[4] = 2

  • 当j == 5时，T[1] ~ T[j - 1]中字符为abab。其中前缀ab和后缀ab相等，通过公式可以推算出k = 3，因此next[5] = 3

  • 当j == 6时，T[1] ~ T[j - 1]中字符为ababa。其中前缀aba和后缀aba相等，因为中间的a可以被前缀和后缀共用。通过公式可以推算出k = 4，因此next[6] = 4

  • 当j == 7时，T[1] ~ T[j - 1]中字符为ababaa。其中前缀a和后缀a相等，通过公式可以推算出k = 2，因此next[7] = 2

  • 当j == 8时，T[1] ~ T[j - 1]中字符为ababaaa。其中前缀a和后缀a相等，通过公式可以推算出k = 2，因此next[8] = 2

  • 当j == 9时，T[1] ~ T[j - 1]中字符为ababaaab。其中前缀ab和后缀ab相等，通过公式可以推算出k = 3，因此next[9] = 3

中间的字符，允许被前缀和后缀共用。所以j == 6时，字符串为ababa，相同的前后缀为aba，而不是a

前缀必须从首字符开始，后缀必须从尾字符开始。所以j == 7时，字符串为ababaa，相同的前后缀为a，而不是ab

4.4 模式串类似于aaaaaaaab

示例：
image.png

  • 当j == 1时，next[1] = 0

  • 当j == 2时，T[1] ~ T[j - 1]中只有字符a，属于其他情况，next[2] = 1

  • 当j == 3时，T[1] ~ T[j - 1]中字符为aa。其中前缀a和后缀a相等，通过公式可以推算出k = 2，因此next[3] = 2

  • 当j == 4时，T[1] ~ T[j - 1]中字符为aaa。其中前缀aa和后缀aa相等，通过公式可以推算出k = 3，因此next[4] = 3

  • 当j == 5时，T[1] ~ T[j - 1]中字符为aaaa。其中前缀aaa和后缀aaa相等，通过公式可以推算出k = 4，因此next[5] = 4

  • 当j == 6时，T[1] ~ T[j - 1]中字符为aaaaa。其中前缀aaaa和后缀aaaa相等，通过公式可以推算出k = 5，因此next[6] = 5

  • 当j == 7时，T[1] ~ T[j - 1]中字符为aaaaaa。其中前缀aaaaa和后缀aaaaa相等，通过公式可以推算出k = 6，因此next[7] = 6

  • 当j == 8时，T[1] ~ T[j - 1]中字符为aaaaaaa。其中前缀aaaaaa和后缀aaaaaa相等，通过公式可以推算出k = 7，因此next[8] = 7

  • 当j == 9时，T[1] ~ T[j - 1]中字符为aaaaaaaa。其中前缀aaaaaaa和后缀aaaaaaa相等，通过公式可以推算出k = 8，因此next[9] = 8

当j的值为3 ~ 9时，中间可被前后缀共用的字符a逐渐变多，所以k值也主键变大

5. 利用代码求解next数组

代码实现：

  1. let t = "abcdex";
  2. let next = getNext(t: t);
  4. func getNext(t : String) -> [Int] {
  6.     var i = -1;
  7.     var j = 0;
  8.     var next = [Int].init(repeating: -1, count: t.count);
  10.     while(j + 1 < t.count){
  12.         if(i == -1 || t[i] == t[j]){
  13.             i += 1;
  14.             j += 1;
  15.             next[j] = i;
  16.             continue;
  17.         }
  19.         i = next[i];
  20.         print("i：\(i)");
  21.     }
  23.     return next;
  24. }

  • 设置默认值：i = -1，j = 0。根据模式串t的长度创建next数组，默认填充-1

    • -1表示模式串中没有可回溯的位置。这种情况模式串重新回到首字符，和主串的下一个字符进行新一轮的匹配

  • 遍历字符串，从索引1 ~ count - 1

  • 当i == -1时

    • i += 1：将i设置为0

    • j += 1：得到下一个索引值

    • next[j] = i：将i值的0赋值到next[1]的位置中

  • 当t[i] == t[j]时

    • i += 1将可回溯的值+1

    • j += 1：得到模式串当前比对字符的下一个索引位置

    • next[j] = i：将可回溯的值，赋值next[j]的位置中

  • 当t[i] != t[j]时

    • i = next[i]：将next[i]中可回溯的值，重新赋值给i。在下一轮循环中，将回溯位置的字符和当前位置的字符再次进行对比

    • 当i值回溯到0时，next[0]中的-1会赋值给i。在下一轮循环中，命中i == -1的逻辑，next[j]会被赋值为0。这意味着当前字符匹配失败后，只能回溯到模式串的首字符

求解代码测试：

  • 模式串abcdex求解，next = [-1, 0, 0, 0, 0, 0]

  • 模式串abcabx求解，next = [-1, 0, 0, 0, 1, 2]

  • 模式串ababaaaba求解，next = [-1, 0, 0, 1, 2, 3, 1, 1, 2]

  • 模式串aaaaaaaab求解，next = [-1, 0, 1, 2, 3, 4, 5, 6, 7]

代码求解的流程概述：

  • 默认next[0] = -1

  • 当i == -1时，表示当前对比从头开始，i += 1，j += 1，next[j] = i

  • 当t[i] == t[j]时，表示对比成功，则i += 1，j += 1，同时next[j] = i，将可回溯的值记录到j位置中

  • 当t[i] != t[j]时，表示对比失败，将i的值回溯到最优位置，则i = next[i]

6. KMP算法的代码实现

代码实现：

let s = "abcacabdc";
let t = "abd";

let next = getNext(t: t);
var i = 0;
var j = 0;

while(i < s.count && j < t.count){

    if(s[i] == t[j]){
        i += 1;
        j += 1;
        continue;
    }

    if(i > s.count - t.count){
        break;
    }

    j = next[j];

    if(j == -1){
        i += 1;
        j = 0;
    }
}

var result = 0;

if(j == t.count){
    result = i - j + 1;
}

print("\(result)");

  • 获取next数组，定义i = 0、j = 0，分别标记主串和模式串的字符索引位置

  • 遍历匹配主串和模式串，当i值查找到主串结尾，且j值查找到模式串结尾，循环停止

  • 当s[i] == t[j]时，当前字符匹配成功，主串和模式串的索引位置分别+1，等待下一轮对比

  • 当s[i] != t[j]时，同时i值超过主串与模式串长度的差值，证明主串已经查找到结尾处。这种情况下出现无法匹配的字符，则证明主串与模式串一定不匹配。此时没必要让主串向后查找，也没必要让模式串回溯，直接退出循环即可

  • 当s[i] != t[j]时，则j = next[j]，让模式串回溯到最优的位置。如果j == -1，证明已经没有可回溯的位置了，此时i += 1让主串向后查找，j = 0将模式串回到首字符位置

  • 遍历结束后，如果j值等于模式串的长度，证明模式串中的字符全部匹配成功，则i - j + 1得到模式串在主串中的起始位置

7. KMP算法的优化

目前KMP算法还存在一些缺陷，具体的表现在某种情况下，会出现不必要的回溯，增加多余的匹配

7.1 算法存在的缺陷

例如：主串：S = "aaaabcdefgxyzz"，模式串T = "aaaaax"

当主串与模式串进入第五次对比时，发现不一致的字符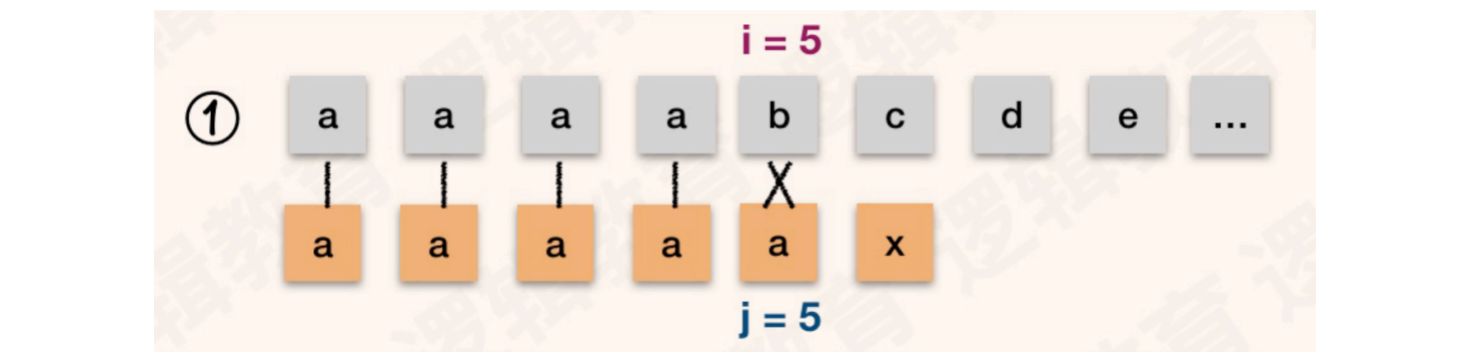
image.png

按照KMP算法的逻辑，j会回溯到4的位置，继续和S[5]进行对比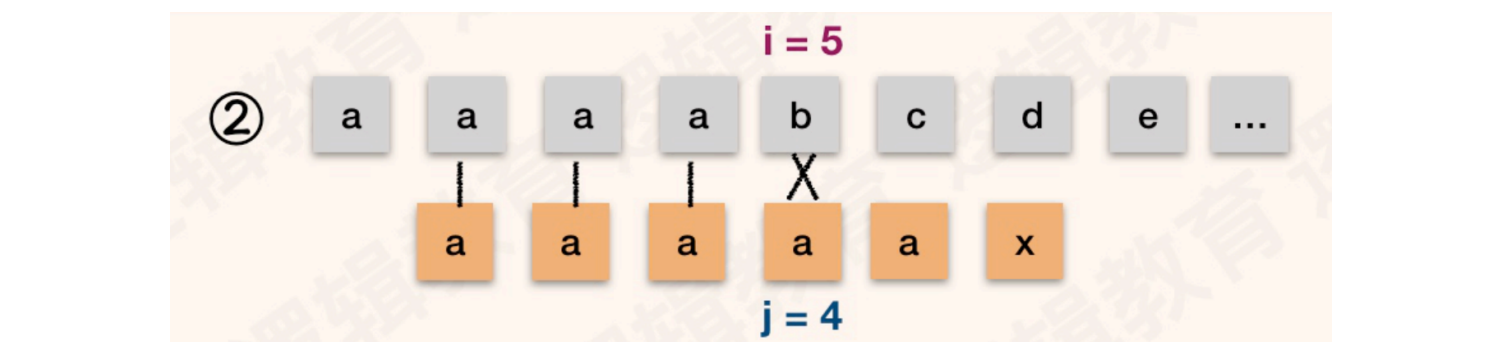
image.png

对比失败，j值回溯到3、2、1位置依次和S[5]进行对比，直到j值无法回溯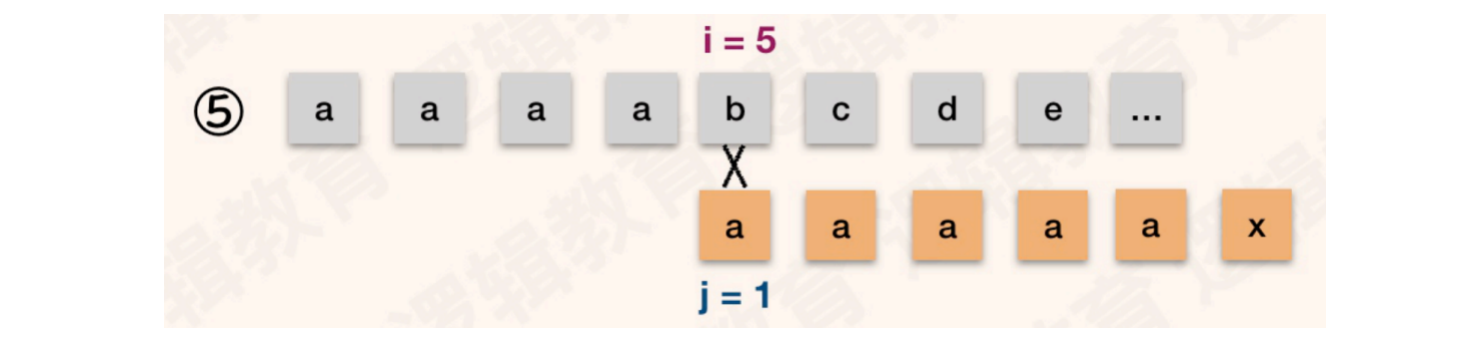
image.png

当j值无法回溯，按照规则，i++，j++，进行S[6] == T[1]的对比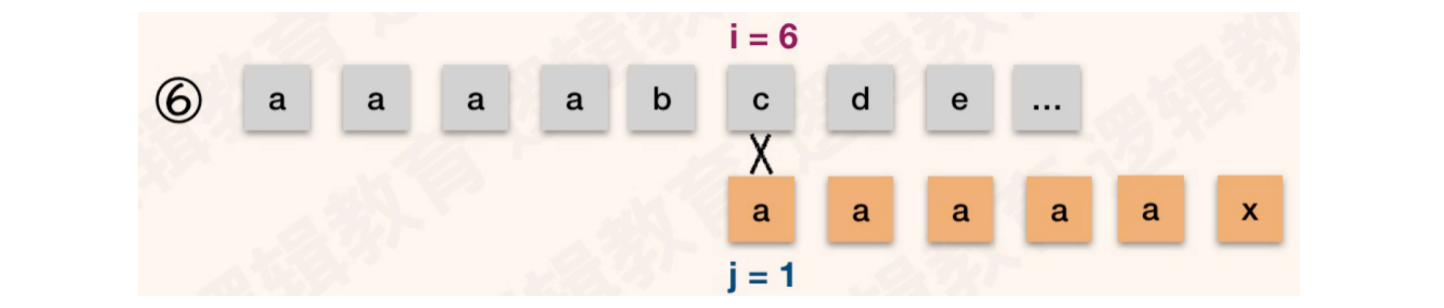
image.png

回顾此流程，当S[5] != T[5]，同时T[5] == T[4] == T[3] == T[2] == T[1]，所以T[5]对比失败后的4次回溯都没有任何意义

当模式串中第2、3、4、5位的字符和首字符a相同，更合理的做法是使用首字符next[1]的值，替代next[2 ~ 5]的回溯值

按照此逻辑，示例中的模式串aaaaax求解，next = [-1, 0, 1, 2, 3, 4]，优化后的结果应该是next = [-1, -1, -1, -1, -1, 4]，从而优化掉几次毫无意义的对比

7.2 算法的优化分析

使用原有的推导逻辑，可以得到next[j]的回溯值，我们可以对其进一步优化

例如：模式串ababc

  • 原有的推导逻辑：当j == 3时，T[1] ~ T[j - 1]中字符为ab。由于a != b，属于其他情况，next[3] = 1

  • 进一步优化逻辑：此时我们得到第三位a的回溯值为1。我们先通过第三位的回溯值，拿到回溯位置上的字符，也就是T[1]首字符的a，然后通过T[1]和当前T[3]进行对比

    • 如果T[1] == T[3]，则next[3]使用next[1]的回溯值，即：next[3] = next[1] = 0

    • 如果T[1] != T[3]，则next[3]的回溯值不改变，即：next[3] = 1

示例：
image.png

  • next数组记录推导出的回溯值，同时新增一个nextval数组，记录优化后的回溯值

  • 当j == 1时，next[1] = 0，nextval[1] = 0

  • 当j == 2时，T[1] ~ T[j - 1]中只有字符a，所以next[2] = 1。优化：由于T[1] != T[2]，则nextval[2] = next[2] = 1

  • 当j == 3时，T[1] ~ T[j - 1]中字符为ab。由于a != b，所以next[3] = 1。优化：由于T[1] == T[3]，则nextval[3] = next[1] = 0

  • 当j == 4时，T[1] ~ T[j - 1]中字符为aba。由于a == a，所以next[4] = 2。优化：由于T[2] == T[4]，则nextval[4] = next[2] = 1

  • 当j == 5时，T[1] ~ T[j - 1]中字符为abab。由于ab == ab，所以next[5] = 3。优化：由于T[3] == T[5]，则nextval[5] = next[3] = 0

  • 当j == 6时，T[1] ~ T[j - 1]中字符为ababa。由于aba == aba，所以next[6] = 4。优化：由于T[4] != T[6]，则nextval[6] = next[6] = 4

  • 当j == 7时，T[1] ~ T[j - 1]中字符为ababaa。由于a == a，所以next[7] = 2。优化：由于T[2] != T[7]，则nextval[7] = next[7] = 2

  • 当j == 8时，T[1] ~ T[j - 1]中字符为ababaaa。由于a == a，所以next[8] = 2。优化：由于T[2] == T[8]，则nextval[8] = next[2] = 1

  • 当j == 9时，T[1] ~ T[j - 1]中字符为ababaaab。由于ab == ab，所以next[9] = 3。优化：由于T[3] == T[9]，则nextval[9] = next[3] = 0

根据上述逻辑，求解next = [0, 1, 1, 2, 3, 4, 2, 2, 3]，优化后的naxtval = [0, 1, 0, 1, 0, 4, 2, 1, 0]

后续在KMP算法中，对模式串进行回溯时，使用优化后的naxtval数组中的回溯值即可

7.3 求解next数组的优化

代码实现：

let t = "ababaaaba";
let next = getNext(t: t);

func getNext(t : String) -> [Int] {

    var i = -1;
    var j = 0;
    var next = [Int].init(repeating: -1, count: t.count);

    while(j + 1 < t.count){

        if(i == -1 || t[i] == t[j]){
            i += 1;
            j += 1;

            if(t[i] == t[j]){
                next[j] = next[i];
                continue;
            }

            next[j] = i;
            continue;
        }

        i = next[i];
    }

    return next;
}

  • 当i == -1或t[i] == t[j]时，则i += 1，j += 1

  • 此后增加优化逻辑，如果t[i] == t[j]，则next[j] = next[i]

  • 如果t[i] != t[j]，执行原有逻辑，next[j] = i

优化后的代码测试：

  • 模式串abcdex求解，next = [-1, 0, 0, 0, 0, 0]

  • 模式串abcabx求解，next = [-1, 0, 0, -1, 0, 2]

  • 模式串ababaaaba求解，next = [-1, 0, -1, 0, -1, 3, 1, 0, -1]

  • 模式串aaaaaaaab求解，next = [-1, -1, -1, -1, -1, -1, -1, -1, 7]

优化后的流程概述：

  • 默认next[0] = -1

  • 当i == -1时，表示当前对比从头开始，i += 1，j += 1

  • 当t[i] == t[j]时，表示对比成功，则i += 1，j += 1

  • 当i和j分别+1后，如果t[i] == t[j]，则next[j] = next[i]。否则t[i] != t[j]，则next[j] = i

  • 当t[i] != t[j]时，表示对比失败，将i的值回溯到最优位置，则i = next[i]

总结

概述：

  • KMP算法的核心是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。本质是通过一个next数组，里面包含了模式串的局部匹配信息，找到模式串中各位置最适合的回溯位置

  • KMP算法的时间复杂度为O(m + n)

算法特点：

  • KMP是在设法利用已知信息，避免将对比位置移回到已经对比过的位置上，而是将它向后移动继续对比，从而提高对比的效率

  • 所以KMP算法的最大特点，就是避免了不必要的回溯发生

  • 算法中i的位置是不需要回溯的，而j的回溯位置，只会取决于模式串T的内容

next数组的推导：

  • next[j]的函数定义，分为以下三种情况：

    • 当j == 1时，next[1] = 0

    • 当前后缀相同时，通过公式p[1] ~ p[k-1] = p[j - k - 1] ~ p[j - 1]可以推算出k = 2，因此next[j] = k

    • 其他情况，next[j] = 1

  • k值的规则：当前后缀相等时，如果前后缀由一个字符组成，则k = 2。如果前后缀由两个字符组成，则k = 3。如果前后缀由N个字符组成，则k = N + 1

  • 中间的字符，允许被前缀和后缀共用

  • 前缀必须从首字符开始，后缀必须从尾字符开始

优化后求解next数组的流程概述：

  • 默认next[0] = -1

  • 当i == -1时，表示当前对比从头开始，i += 1，j += 1

  • 当t[i] == t[j]时，表示对比成功，则i += 1，j += 1

  • 当i和j分别+1后，如果t[i] == t[j]，则next[j] = next[i]。否则t[i] != t[j]，则next[j] = i

  • 当t[i] != t[j]时，表示对比失败，将i的值回溯到最优位置，则i = next[i]

KMP算法的代码实现：

  • 获取next数组，定义i = 0、j = 0，分别标记主串和模式串的字符索引位置

  • 遍历匹配主串和模式串，当i值查找到主串结尾，且j值查找到模式串结尾，循环停止

  • 当s[i] == t[j]时，当前字符匹配成功，主串和模式串的索引位置分别+1，等待下一轮对比

  • 当s[i] != t[j]时，同时i值超过主串与模式串长度的差值，证明主串已经查找到结尾处。这种情况下出现无法匹配的字符，则证明主串与模式串一定不匹配。此时没必要让主串向后查找，也没必要让模式串回溯，直接退出循环即可

  • 当s[i] != t[j]时，则j = next[j]，让模式串回溯到最优的位置。如果j == -1，证明已经没有可回溯的位置了，此时i += 1让主串向后查找，j = 0将模式串回到首字符位置

  • 遍历结束后，如果j值等于模式串的长度，证明模式串中的字符全部匹配成功，则i - j + 1得到模式串在主串中的起始位置