1. 散列技术
散列技术是记录的存储位置和它的关键字之间建⽴⼀个确定的对应关系f,使得每个关键字key对应⼀个存储位置f(key)。 查找时,根据这个对应关系找到给定值key的映射f(key)。若查找集合中存在这个记录,则必定在f(key)的位置上
散列技术的优势,可以避免查找时的遍历过程,通过一个关系公式,直接获得元素的存储位置。即:存储位置 = f(关键字),这里的f称之为散列函数,或哈希函数
散列技术存储的元素,它们之间没有逻辑关系,也没有先后顺序
使用散列技术,要符合以下规则:
存储时,通过散列函数,计算并保存散列地址
查找时,将
key传入散列函数,得到散列地址。通过散列地址,直接获取对应的元素
2. 散列函数
使用散列技术是一种解决问题的思想,面对不同需求,散列函数的公式也会完全不一样
散列函数要满足以下需求:
简单,并且均匀,存储利用率高(关键)
散列表适合定向查找,不适合大范围的查找
实现一个散列函数时,公式的设计主要考虑以下几点:
关键字的长度
散列表的大小
计算散列地址所需的时间
关键字的分布情况
记录查找的概率
2.1 直接定址法
直接定址法:是以数据元素关键字本身或它的线性函数作为它的哈希地址。适合较小的散列表,并且key值连续。优势:简单,分布均匀,不容易产生哈希冲突。缺陷:必须提前知道关键字的分布情况
假设,从一张表中,按照年龄0 ~ 100统计人数,此时年龄可以直接作为关键字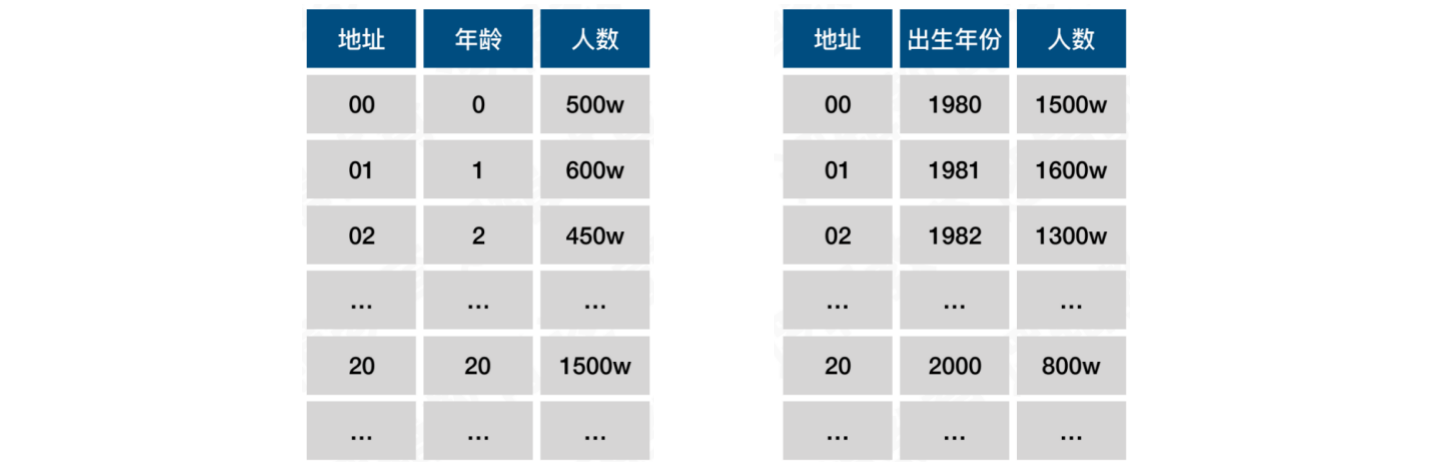
按照上述需求,可以将公式定义为:f(key) = key
我们只需按0 ~ 100开辟连续空间,每个空间中存储对应人数。当查找3岁的人数时,通过公式f(3) = 3,直接从位置3拿到对应人数即可
如果需求变更为通过出生年份查找人数,例如:查找key = 1980,得到对应的人数1500w。此时公式f(key) = key则不适用,因为它会开辟大量的空间,造成空间浪费
我们可将公式优化为:f(key) = key - 1980,通过散列函数,将年份key对应到0 ~ 100的位置上
通常我们希望存储分布均匀,会采用以下公式:f(key) = a * key + b,其中a、b为常数
2.2 数字分析法
数字分析法:如果关键字是位数较多的数字(比如手机号),且这些数字部分存在相同规律,则抽取剩余不同规律部分作为散列地址
假设,公司批量办理sim卡,此时手机号码是连续的,区别仅为号码的后四位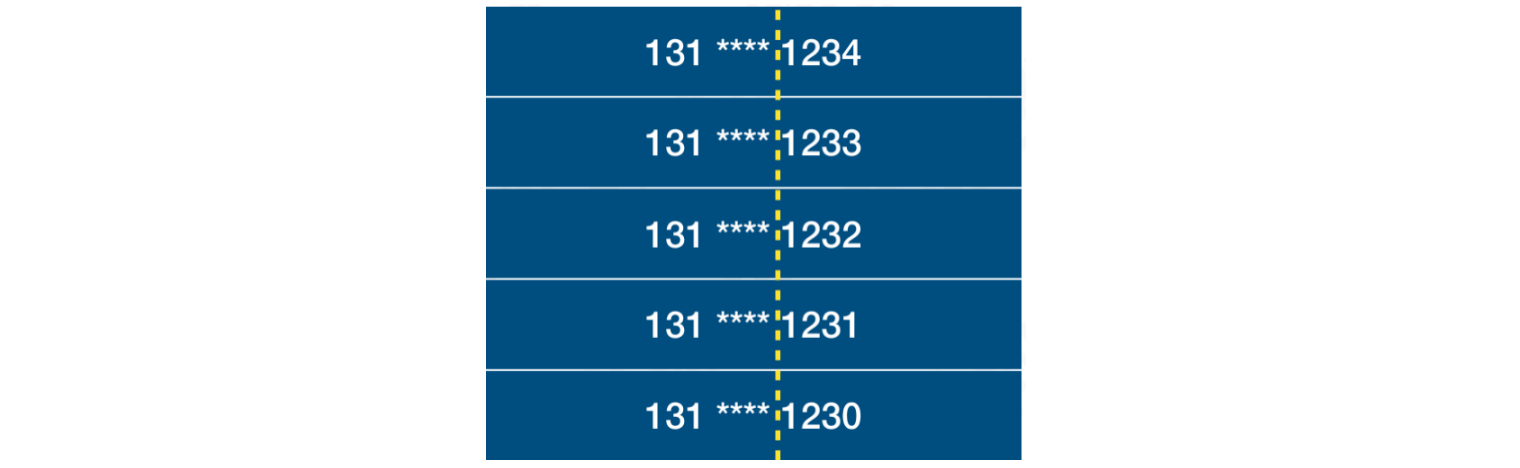
按照上述需求设计哈希函数,我们可以将号码的关键位,也就是后四位,按照某种组合转变为散列地址。例如:翻转、位移、累加。但组合出的数字越小,越容易产生哈希冲突
2.3 平方取中法
平方取中法:即取关键字平方的中间位数作为散列地址
公式: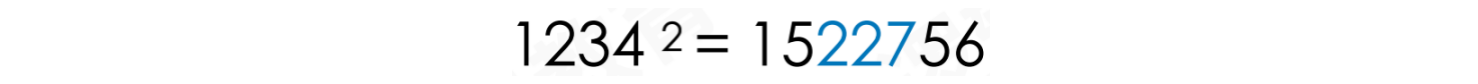
假设key = 1234,对其进行平方,将结果作为散列地址。它的缺点是得到的地址会比较长,所以我们可以获取它的中间部分作为地址。这种方式称之为平方取中法
例如:key值为1234或9876,如果使用直接定址法,需要开辟很大的空间,并且数据分布不均匀。如果使用平方取中法,可以一定程度上让地址的分布变得均匀,也不会增加哈希冲突的概率
2.4 折叠法
折叠法:就是将关键字从左到右分割成位数相等的⼏部分(注意最后⼀部分位数不够可以稍微短些),然后将⼏部分叠加求和,并按散列表表⻓,取后⼏位作为散列地址。它适合数字位数较长的情况,并且我们无法预知数字的分布情况
示例: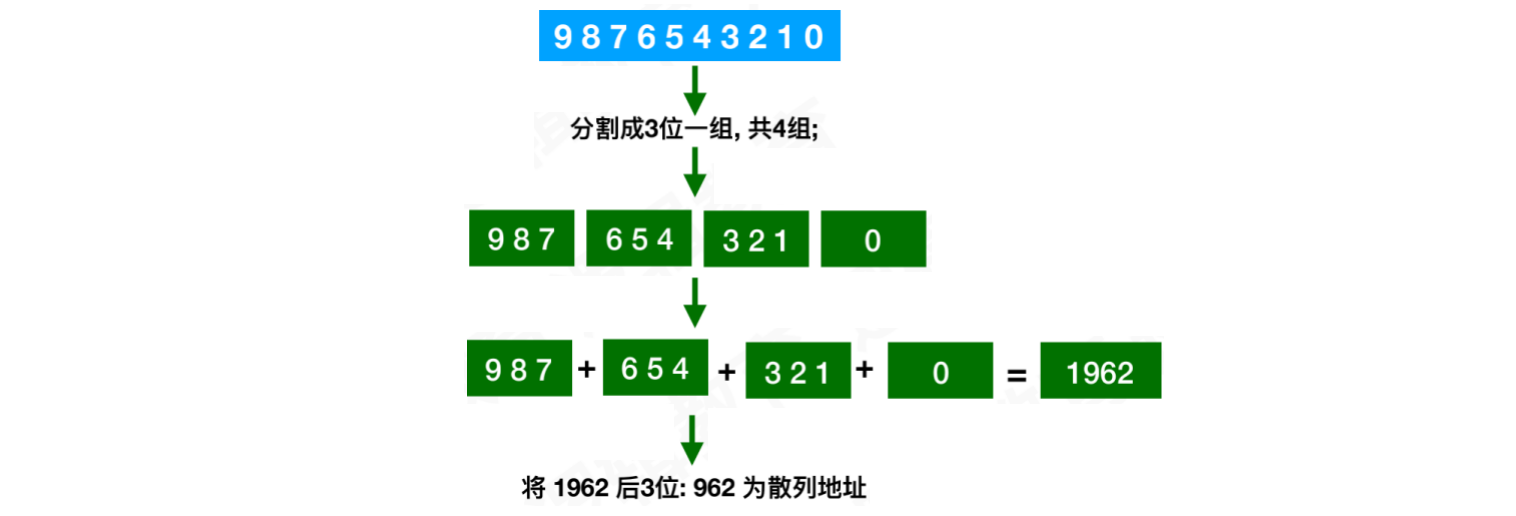
2.5 除留余数法
除留余数法:最常用的散列函数方法,该方法的关键就在于选择合适的p。根据前辈们的经验,若散列表表长为m,通常p为小于或等于表长(最好接近)的最小质数或不包含小于20质因子的合数
将key模以p,得到的余数作为散列地址
例如:p = 12,使用相同方式进行存取,读取时只需要用key值模以12,即可得到下标
这种方式在开发中是最长用到的,但是要处理好它的哈希冲突问题。例如:当key值为12的倍数时,余数都为0,此时就会产生哈希冲突
2.6 随机地址法
随机地址法:取关键字的随机函数值为它的散列地址。这里的随机其实是伪随机,设定的随机种子数相同,会产生相同的随机数。这种方式适用于关键字的长度不等的场景
公式: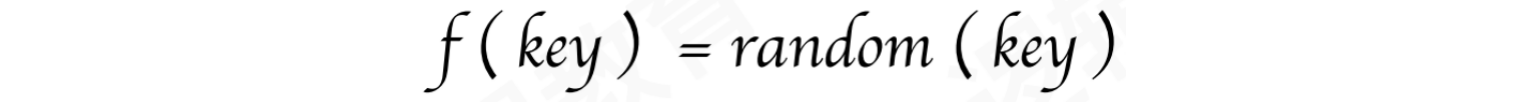
3. 哈希冲突
哈希冲突:即关键字不同的元素,被映射到了同一个内存位置
任何一种哈希算法,都有可能产生哈希冲突。哈希冲突就像疾病一样,只能尽量预防,但无法绝对避免
3.1 开放定址法
开放定址法:就是⼀旦发⽣了冲突,就去寻找下⼀个空的散列地址。只有散列表⾜够⼤,空的散列地址总能找到,并将记录存⼊
3.1.1 线性探测法
线性探测法:当我们的所需要存放值的位置被占了,我们就往后面一直加1并对m取模直到存在一个空余的地址供我们存放值,取模是为了保证找到的位置在0 ~ (m - 1)的有效空间之中
公式:
假设:关键字集合为{12, 67, 56, 16, 25, 37, 22, 29, 15, 47, 48, 34},表⻓为12。散列函数公式使用除留余数法:f(key) = key mod 12
当计算key = 37时,f(37) = 1,与25发⽣冲突。使⽤开放定址公式:f(37) = (f(37) + 1) mod 12 = 2,此时下标为2的位置是空的,即可直接存储
后续的{22, 29, 15, 47},使用f(key) = key mod 12没有产生哈希冲突,即可直接存储
当计算f(48) = 48 mod 12 = 0,此时位置0上已经存储了数据12,那么12和48就是同义词了
使⽤开放定址法公式f(48) = (f(48) + 2) mod 12 = 1,于是又和25发⽣冲突了
使⽤开放定址法公式,继续计算新的散列地址。直到f(48) = (f(48) + 6 ) mod 12 = 6时,此时位置6上没有数据,则将48存储到下标为6的位置上
当使用线性探测法时,计算f(34) = 10,和22发⽣了冲突。此时位置10以后已经没有空间了,但是位置10之前还有空间。通过公式⼀直取模求余,最终也能得到结果,将34存储到位置9上,但是这样的计算效率⾮常低下
3.1.2 ⼆次探测法
二次探测法:当我们的所需要存放值的位置被占了,会前后寻找而不是单独方向的寻找
公式: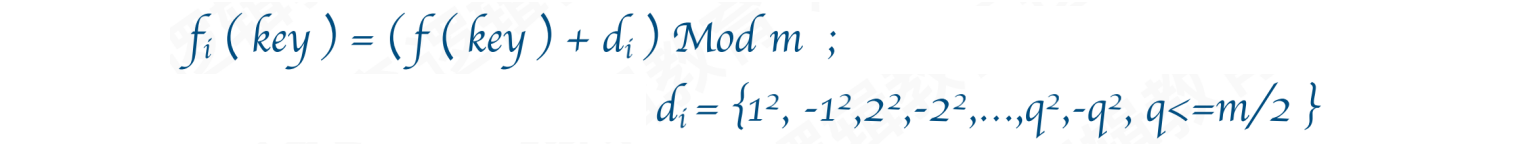
di = {1 ^ 2, -1 ^ 2, 2 ^ 2, -2 ^ 2 … q ^ 2, -q ^ 2, q <= m / 2}
使用公式f(34) = (f(34) + 1) mod 12 = 11计算,和47发⽣了冲突
继续计算,f(34) = (f(34) - 1) mod 12 = 9,此时位置9是空的,即可直接存储
3.2 再散列函数法
再散列函数法:当发生哈希冲突时,可以使用第二个、第三个……等其他的散列函数计算地址,直到解决冲突为止。这种方式虽然降低冲突概率,但是增加了计算时间
公式: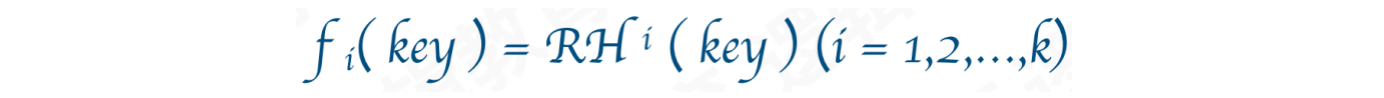
RHi:指的是不同的散列函数
3.3 链地址法
链地址法:俗称拉链法。它会将所有的关键字为同义词的记录存储在⼀个单链表中,我们称之为同义词⼦表。在散列表中只存储所有同义词⼦表的头指针(首地址)
上述案例,使用链地址法会存储为以下结构: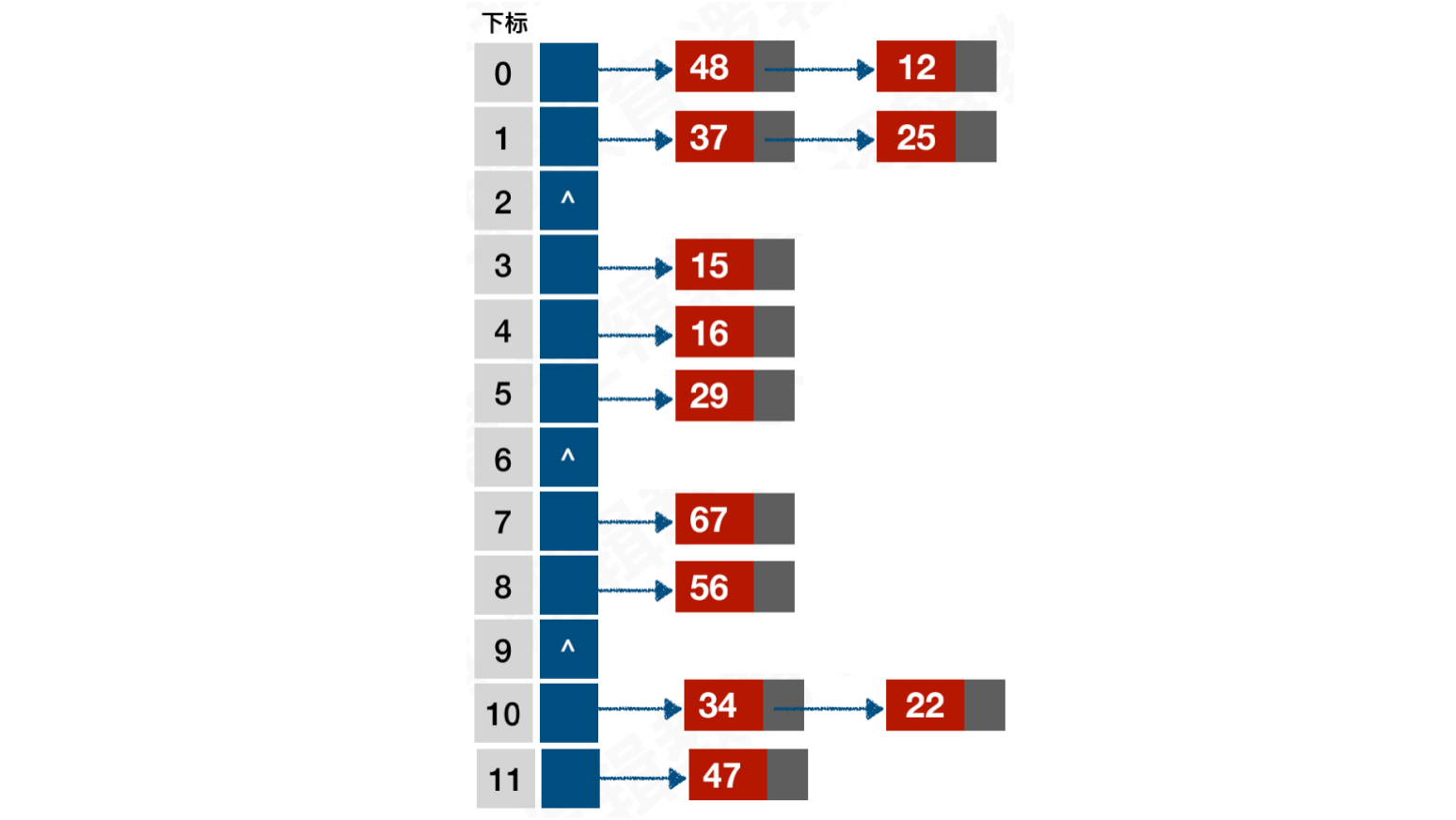
- 通过公式获取下标,通过下标获取链表,然后在链表中进行查找,返回指定元素。如果当前下标没有发生哈希冲突,同义词⼦表中只会存在一个元素,即可直接找到。否则,需要进行链表的遍历
3.4 公共溢出法
公共溢出法:将哈希表分为基本表和溢出表,将发生冲突的都存放在溢出表中
当发生哈希冲突时,就会创建溢出表,将冲突的元素存储在溢出表中。查找时,优先基本表,未找到再从溢出表中进行查找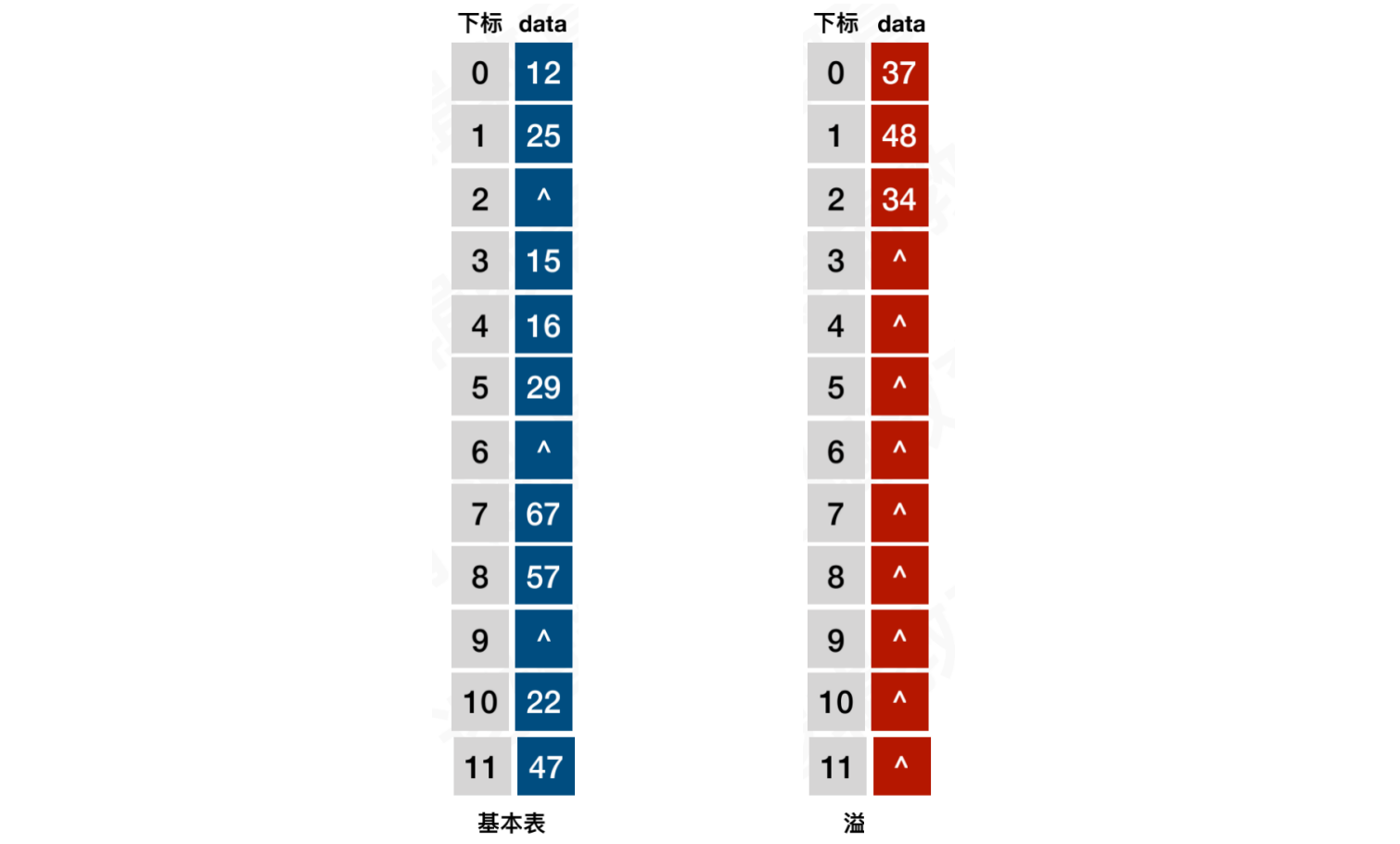
- 这种方式并不好,可能会造成大量的空间浪费,日常开发中很少被使用到
4. 实现散列查找
使用一个数组作为散列表,使用除留余数法作为散列函数,使用线性探测法解决哈希冲突
4.1 初始化
class HashTable {// 使用一个数组作为散列表fileprivate var _arr : [Int?]?;// 散列表大小fileprivate var _count : Int;// 初始化init(count : Int){_arr = [Int?].init(repeating: nil, count: count);_count = count;}// 散列函数fileprivate func getHash(key : Int) -> Int {// 除留余数法return key % _count;}// 解决哈希冲突fileprivate func linearProbing(address : inout Int) {// 线性探测法address = (address + 1) % _count;}}
4.2 关键字插入
class HashTable {
// 将关键字插入散列表
func insert(key : Int) {
// 通过散列函数获取地址
var address = getHash(key: key);
// 通过地址,从散列表中获取数据
var value = _arr![address];
// 如果当前地址已存在数据,遍历找到空地址为止
while(value != nil){
// 使用线性探测法,再次计算地址
linearProbing(address: &address);
// 通过新地址,从散列表中获取数据
value = _arr![address];
}
// 将关键字插入散列表
_arr![address] = key;
}
}
4.3 关键字在散列表中的地址
class HashTable {
// 关键字在散列表中的地址
func getAddress(key : Int) -> Int? {
// 通过散列函数获取地址
var address = getHash(key: key);
// 将首次计算出的地址临时记录一份
let tmp = address;
// 通过地址,从散列表中获取数据
var value = _arr![address];
// 如果数据和传入的关键字不相等,有可能是哈希冲突导致,继续遍历查找
while(value != key){
// 使用线性探测法,再次计算地址
linearProbing(address: &address);
// 通过新地址,从散列表中获取数据
value = _arr![address];
// 如果地址为空,证明关键字不存在
// 如果再哈希的地址 等于 首次计算出的地址,证明已经查找过一轮,关键字不存在
if(value == nil || address == tmp){
return nil;
}
}
return address;
}
}
总结
散列技术:
散列技术是记录的存储位置和它的关键字之间建⽴⼀个确定的对应关系
f,使得每个关键字key对应⼀个存储位置f(key)查找时,根据这个对应关系找到给定值
key的映射f(key)。若查找集合中存在这个记录,则必定在f(key)的位置上散列技术的优势,可以避免查找时的遍历过程,通过一个关系公式,直接获得元素的存储位置。即:存储位置 = f(关键字),这里的
f称之为散列函数,或哈希函数散列技术存储的元素,它们之间没有逻辑关系,也没有先后顺序
使用散列技术,要符合以下规则:
存储时,通过散列函数,计算并保存散列地址
查找时,将
key传入散列函数,得到散列地址。通过散列地址,直接获取对应的元素
散列函数:
散列函数要满足以下需求:
简单,并且均匀,存储利用率高(关键)
散列表适合定向查找,不适合大范围的查找
实现一个散列函数时,公式的设计主要考虑以下几点:
关键字的长度
散列表的大小
计算散列地址所需的时间
关键字的分布情况
记录查找的概率
散列函数的常用方法:
直接定址法:是以数据元素关键字本身或它的线性函数作为它的哈希地址。适合较小的散列表,并且
key值连续。优势:简单,分布均匀,不容易产生哈希冲突。缺陷:必须提前知道关键字的分布情况数字分析法:如果关键字是位数较多的数字(比如手机号),且这些数字部分存在相同规律,则抽取剩余不同规律部分作为散列地址
平方取中法:即取关键字平方的中间位数作为散列地址
折叠法:就是将关键字从左到右分割成位数相等的⼏部分(注意最后⼀部分位数不够可以稍微短些),然后将⼏部分叠加求和,并按散列表表⻓,取后⼏位作为散列地址。它适合数字位数较长的情况,并且我们无法预知数字的分布情况
除留余数法:最常用的散列函数方法,该方法的关键就在于选择合适的
p。根据前辈们的经验,若散列表表长为m,通常p为小于或等于表长(最好接近)的最小质数或不包含小于20质因子的合数随机地址法:取关键字的随机函数值为它的散列地址。这里的随机其实是伪随机,设定的随机种子数相同,会产生相同的随机数。这种方式适用于关键字的长度不等的场景
哈希冲突:
哈希冲突:即关键字不同的元素,被映射到了同一个内存位置
任何一种哈希算法,都有可能产生哈希冲突。哈希冲突就像疾病一样,只能尽量预防,但无法绝对避免
解决哈希冲突的常用方法:
开放定址法:就是⼀旦发⽣了冲突,就去寻找下⼀个空的散列地址。只有散列表⾜够⼤,空的散列地址总能找到,并将记录存⼊
线性探测法:当我们的所需要存放值的位置被占了,我们就往后面一直加
1并对m取模直到存在一个空余的地址供我们存放值,取模是为了保证找到的位置在0 ~ (m - 1)的有效空间之中二次探测法:当我们的所需要存放值的位置被占了,会前后寻找而不是单独方向的寻找
再散列函数法:当发生哈希冲突时,可以使用第二个、第三个……等其他的散列函数计算地址,直到解决冲突为止。这种方式虽然降低冲突概率,但是增加了计算时间
链地址法:俗称拉链法。它会将所有的关键字为同义词的记录存储在⼀个单链表中,我们称之为同义词⼦表。在散列表中只存储所有同义词⼦表的头指针(首地址)
公共溢出法:将哈希表分为基本表和溢出表,将发生冲突的都存放在溢出表中

