1. 归并排序

归并排序（Merging Sort）：就是利⽤归并的思想实现排序⽅法。它的原理是假设初始序列含有n个记录，则可以看成n个有序的⼦序列，每个⼦序列的⻓度为1，然后两两合并。得到n / 2个⻓度为2或1的有序⼦序列，再两两归并。如此重复，直到得到⼀个⻓度为n的有序序列为止，这种排序⽅法称为2路归并排序

示例：将字符串拆解，将它们看成N个子序列，再两两合并，然后排序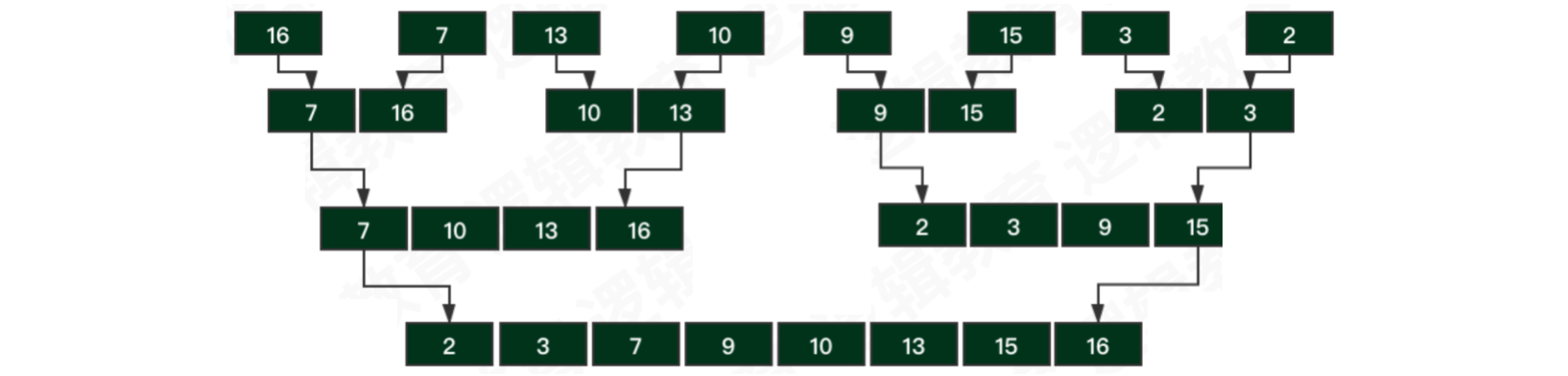
image.png

  • 【步骤一】拆解：将数组中的元素，按照2倍规则拆解成的独立⼦序列

  • 【步骤二】归并：将⼦序列两两合并，合并过程中同时排序，使其合并后变为有序

如此重复，直到得到⼀个⻓度为n的有序序列为止

1.1 思路分析

归并排序需要低位low和高位hight双指针，低位默认指向数组的起始位置，高位默认执行数组的结束位置。除此之外，还需要一个额外的mid指针，指向数组的拆解位置

通过递归与三个指针的配合，将数组拆解成一个一个的独立有序的⼦序列

  • 递归条件：low != hight，则持续递归

  • mid指针的公式：mid = (low + hight) / 2 = (1 + 9) / 2 = 5

假设：对一个序列进行排序：[50, 10, 90, 30, 70, 40, 80, 60, 20]

【拆解】第一次拆解：low = 1，hight = 9，mid = (low + hight) / 2 = (1 + 9) / 2 = 5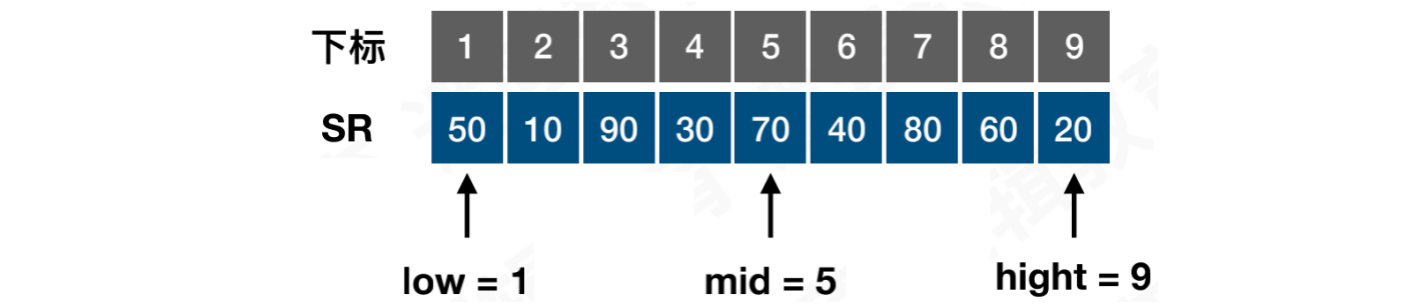
image.png

将序列拆分成两部分，左侧范围[low, mid] = [1, 5]，右侧范围[mid + 1, hight] = [6, 9]

第二次拆解：分别对左、右两个子序列继续拆解，以左侧子序列为例：low = 1，hight = 5，mid = 3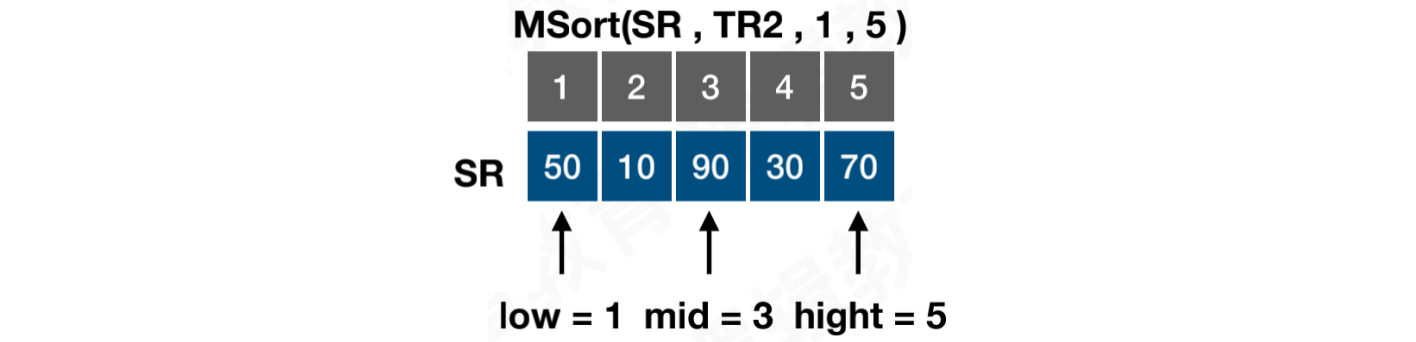
image.png

第三、四次拆解：按同样的方式继续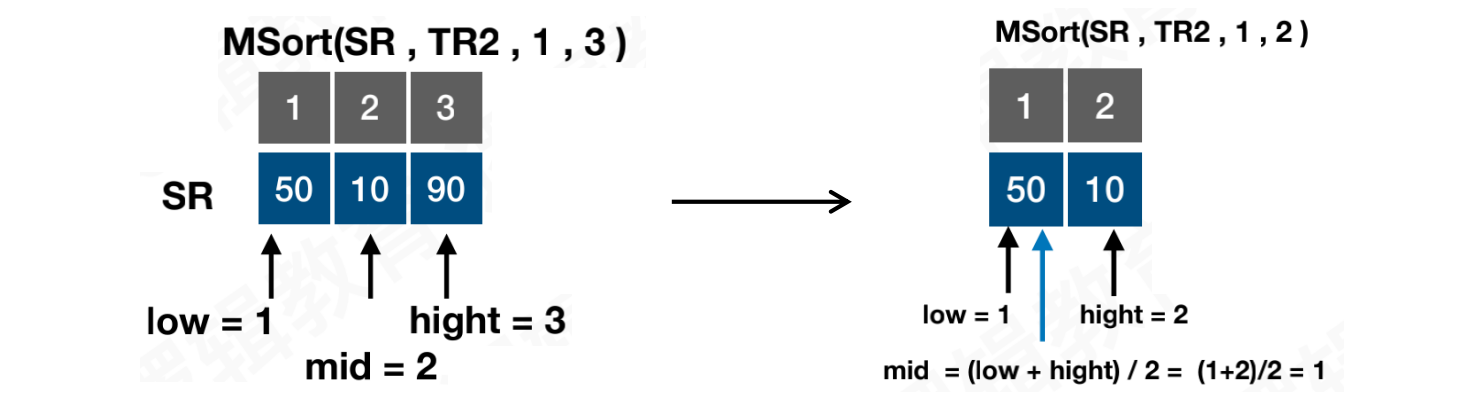
image.png

第五次拆解：此时low == hight，满足递归的停止条件，开始回溯流程
image.png

而右侧子序列的拆解逻辑也是同理

【归并】在递归的回溯流程中，开始对子序列进行合并

合并的过程，由下子上，依次将子序列合并为有序序列

以最后一层子序列的合并为例：此时我们得到两个各自有序的子序列，需要将其合并成一个整体有序的序列

第一次比较，此时i = 1，j = 6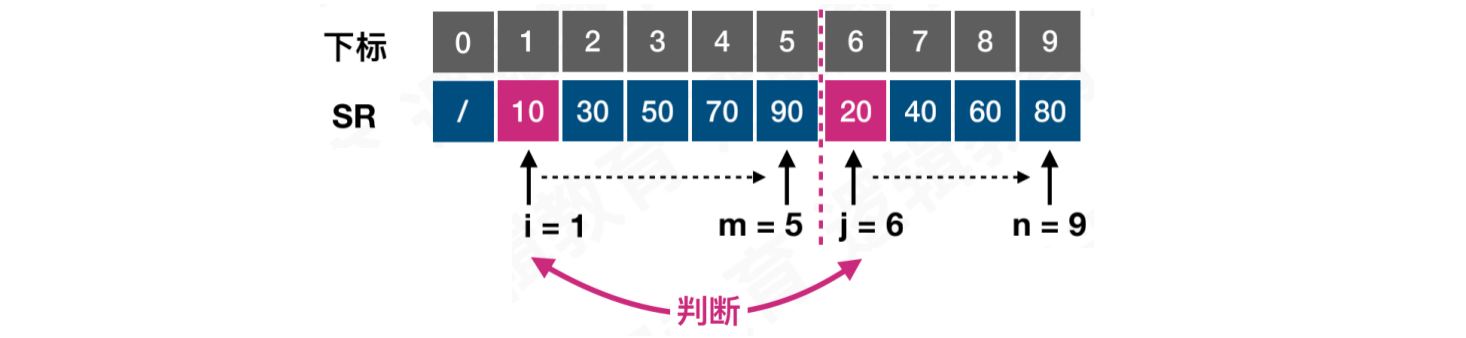
image.png

比较i与j位置的元素，将较小的值存储在结果数组的k位置中，默认k = i，每记录一个结果，k += 1。如果位置i的值较小，则i += 1。反之，j += 1
image.png

第二次比较，此时i = 2，j = 6，k = 2。位置j的值较小，将20记录到，结果数组的k位置中，j += 1，k += 1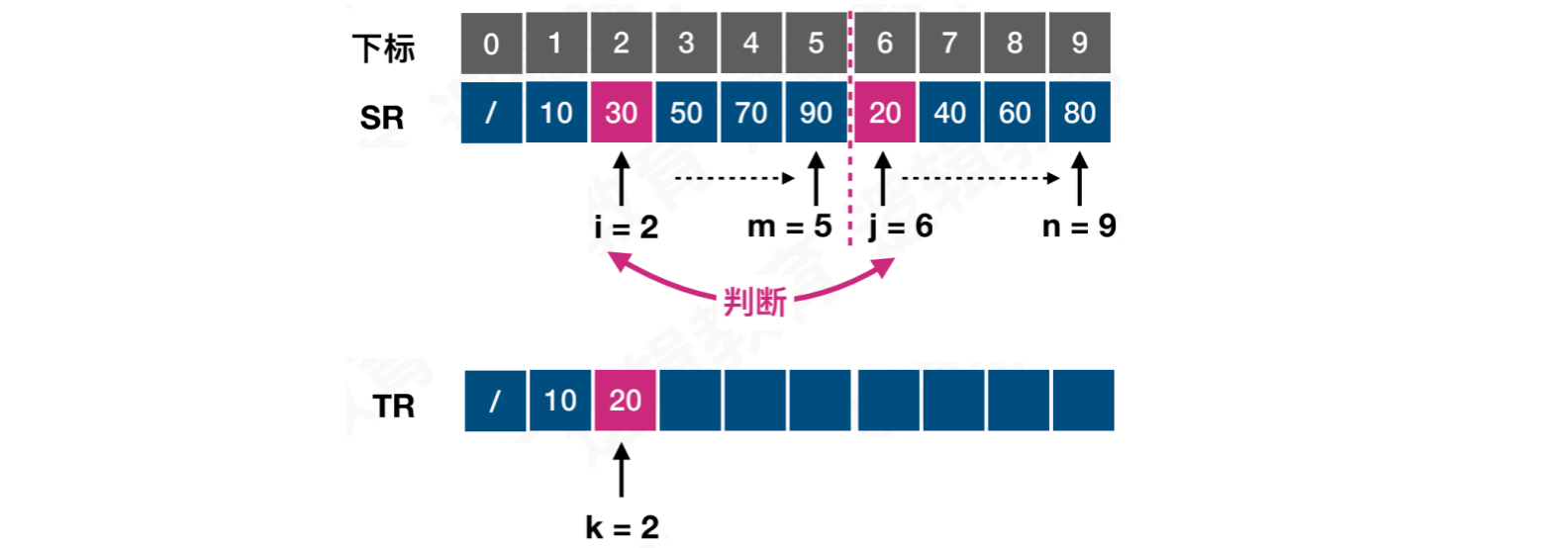
image.png

第三次比较，此时i = 2，j = 7，k = 3。位置i的值较小，将30记录到，结果数组的k位置中，i += 1，k += 1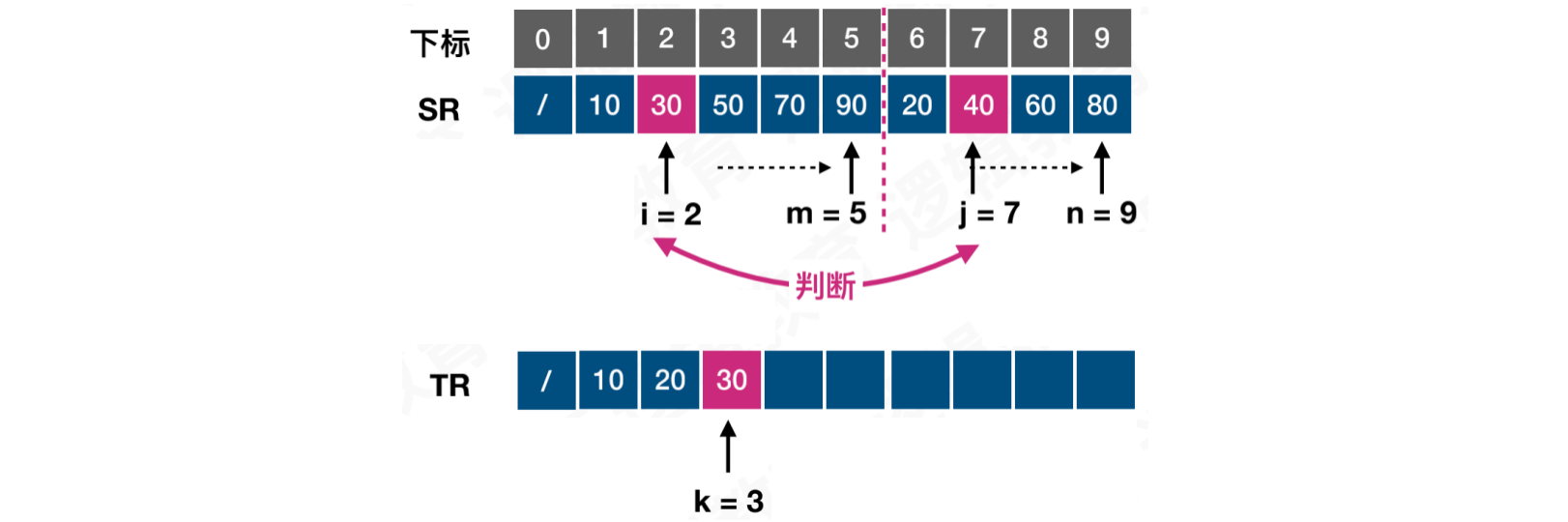
image.png

第三次比较，此时i = 2，j = 1，k = 2。位置j的值较小，将20记录到，结果数组的k位置中，j += 1，k += 1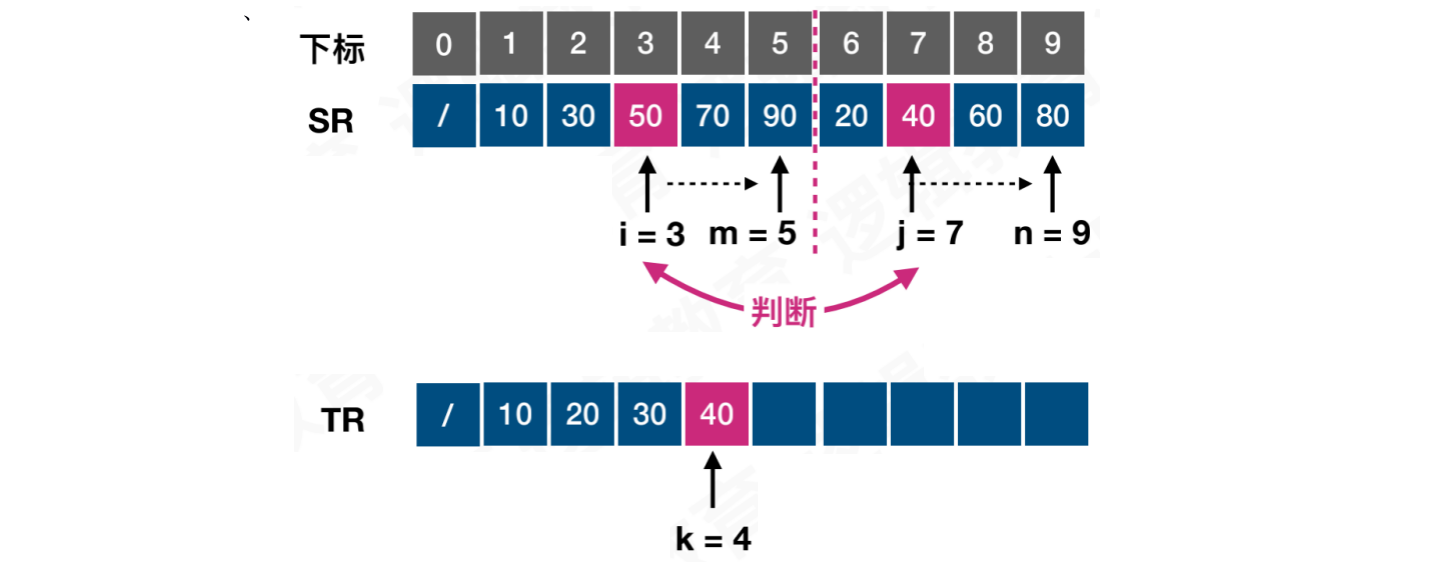
image.png

按照上述逻辑，持续对比，直到其中一个子序列中所有元素全部有序的记录到结果数组中为止。然后将另一个子序列的剩余元素，按照顺序依次记录到结果数组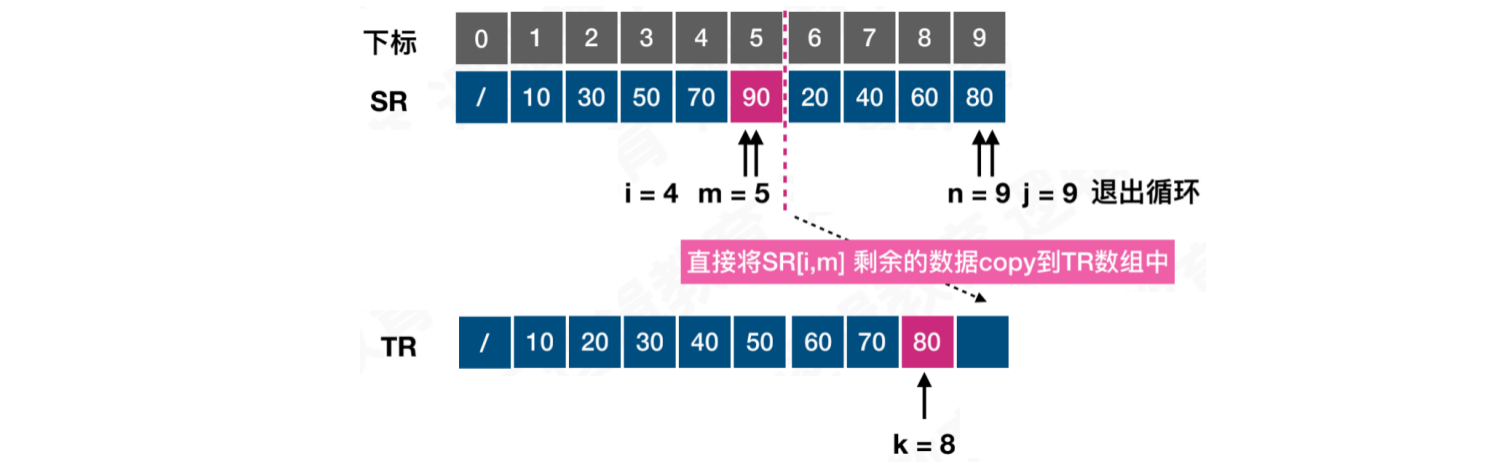
image.png

最终结果数组成为一个⻓度为n的有序序列

1.2 代码实现

拆解函数：

  1. class Sort<Element : Comparable> {
  3.     // 拆解函数
  4.     fileprivate func mSort(result: inout [Element?], low: Int, hight: Int){
  6.         // 当低位指针与高位指针相遇，停止递归
  7.         if(low == hight){
  8.             // 将该位置元素写入结果数组
  9.             result[low] = _arr[low];
  10.             return;
  11.         }
  13.         // 创建临时数组，开辟n的长度，默认填充nil
  14.         var tmp = [Element?].init(repeating: nil, count: _arr.count);
  15.         // 计算mid指针的位置
  16.         let mid = (low + hight) / 2;
  17.         // 将临时创建的数组传入本次递归方法中，并传入左侧子序列的范围[low, mid]
  18.         mSort(result: &tmp, low: low, hight: mid);
  19.         // 将临时创建的数组传入本次递归方法中，并传入右侧子序列的范围[mid + 1, hight]
  20.         mSort(result: &tmp, low: mid + 1, hight: hight);
  22.         // 进入递归回溯流程
  23.         // 调用归并方法，tmp是下层递归回溯的结果，result是本次方法的入参
  24.         // 将排序合并后的结构，写入result中，通过递归的层层回溯，最后形成完整的有序序列
  25.         merge(tmp: tmp, result: &result, low: low, mid: mid, hight: hight);
  26.     }
  27. }

归并函数：

class Sort<Element : Comparable> {

    // 归并函数
    fileprivate func merge(tmp: [Element?], result: inout [Element?], low: Int, mid: Int, hight: Int){

        var i = low;
        let m = mid;
        let n = hight;

        var j = m + 1;
        var k = i;

        // i和j都没有移动到末尾，则持续对比
        while(i <= m && j <= n){

            // 位置i元素较小
            if(tmp[i]! < tmp[j]!){
                // 将位置i元素记录到结果数组的k位置
                result[k] = tmp[i];
                // i向后移动
                i += 1;
            }
            // 位置j元素较小
            else if(tmp[i]! >= tmp[j]!){
                // 将位置j元素记录到结果数组的k位置
                result[k] = tmp[j];
                // j向后移动
                j += 1;
            }

            // k向后移动
            k += 1;
        }

        // 如果左侧子序列中存在剩余元素
        if(i <= m){
            // 按顺序将元素依次记录到结果数组
            for l in i...m {
                result[k] = tmp[l];
                // k向后移动
                k += 1;
            }
        }

        // 如果右侧子序列中存在剩余元素
        if(j <= n){
            // 按顺序将元素依次记录到结果数组
            for l in j...n {
                result[k] = tmp[l];
                // k向后移动
                k += 1;
            }
        }
    }
}

归并排序：

class Sort<Element : Comparable> {

    // 归并排序
    func mergingSort() {

        // 低位指针默认为1
        let low = 1;
        // 高位指针默认为n - 1
        let hight = _arr.count - 1;
        // 创建结果数组，开辟n的长度，默认填充nil
        var result = [Element?].init(repeating: nil, count: _arr.count);
        // 调用拆解函数
        mSort(result: &result, low: low, hight: hight);
        // 将排序后的结果赋值给原数组
        _arr = result;
    }
}

时间复杂度：⼀趟归并需要将_arr[1] ~ _arr[n]中相邻⻓度为n的有序序列的进⾏两两⽐较，并将结果存储在result[1] ~ tmp[n]。这需要将待排序的所有记录扫描⼀遍，因此耗费O(n)时间。⽽由于完全⼆叉树的深度可知，整个归并排序需要进⾏log2n次，因此总的时间复杂度为O(nlogn)，是归并排序最好、最坏、平均时间复杂度的性能

空间复杂度：由于递归排序在递归的过程中，需要存储与原始序列同样数量的归并结果，以及递归时深度为log2n的栈空间，因此空间复杂度为O(n + log2n)

1.3 非递归实现

非递归的拆解方式与递归有所不同，不需要每次砍半，直接使用相邻元素归并即可

第一次拆解归并：
image.png

第二次拆解归并：
image.png

第三次拆解归并：
image.png

第四次拆解归并：
image.png

拆解函数：

class Sort<Element : Comparable> {

    // 拆解函数
    fileprivate func mSort(result: inout [Element?], low: inout Int, hight: inout Int){

        // 默认将原始数组赋值给结果数组
        result = _arr;
        // 拆解的最小单位默认为1
        var multiple = 1;

        // 如果扩大一倍没有超过序列长度，进行拆解归并
        while(multiple * 2 < _arr.count){

            // 拆解单位扩大一倍
            multiple = multiple * 2;
            // 拆解归并的次数，默认为0
            var index = 0;

            // 拆解的起始位置没有超过序列长度，进行拆解归并
            while(index * multiple + 1 < _arr.count) {

                // 计算低位
                let low = index * multiple + 1;
                // 计算高位
                var hight = low + multiple - 1;
                // 计算mid值
                var mid = (low + hight) / 2;

                // 如果高位超过序列长度
                if(hight >= _arr.count){

                    // 剩余元素小于当前倍数的一半，表示右侧子序列仅剩下一个
                    if(_arr.count - low < multiple / 2){
                        // 退出循环，等待外部进行最后一次归并
                        break;
                    }

                    // 否则，表示右侧子还剩下两个待合并的子序列

                    // 重新计算高位
                    hight = _arr.count - 1;
                    // 重新计算mid值
                    mid = low + multiple / 2 - 1;
                }

                // 将子序列归并，每一次的归并结果都会覆盖result数组中
                merge(tmp: result, result: &result, low: low, mid: mid, hight: hight);
                // 拆解归并的次数+1
                index += 1;
            }
        }

        // 进行最后一次归并
        merge(tmp: result, result: &result, low: 1, mid: multiple, hight: _arr.count - 1);
    }
}

2. 快速排序

快速排序（Quick Sort）的基本思想：通过⼀趟排序将待排序记录分割成独⽴的两部分。其中⼀部分记录的关键字均为另⼀部分记录的关键字⼩，则可分别对两部分记录继续进⾏排序，以达到整个序列有序的⽬的

2.1 思路分析

【对子表进行排序】假设，我们从序列中找到一个元素作为枢轴
image.png

通过某种方式，让左侧低子表的数据小于枢轴，让右侧高子表的数据大于枢轴
image.png

然后对低⼦表和⾼⼦表分别排序

【求解枢轴】使用双指针，低位指针默认指向序列起始位置，高位指针默认指向序列的结束位置
image.png

我们将序列整体看做一张子表，选择⼦表中第一个元素作为枢轴变量，此时pivotkey = 50

从表的两端往中间扫描，开始第⼀层循环，循环判断依据是low < high

_arr[high]与pivotkey进⾏⽐较，如果low<hight并且_arr[high] >= pivotkey就递减high

判断依据：_arr[high] >= pivotkey && low < high循环则继续往下查找，high -= 1向前移动

⽤⾼位high的元素与pivotkey进⾏⽐较，找到⽐它⼩的元素，将⽐枢轴记录⼩的记录交换到低端位置上
image.png

此时_arr[9] < 50，则退出循环，退出后交换low与high位置的元素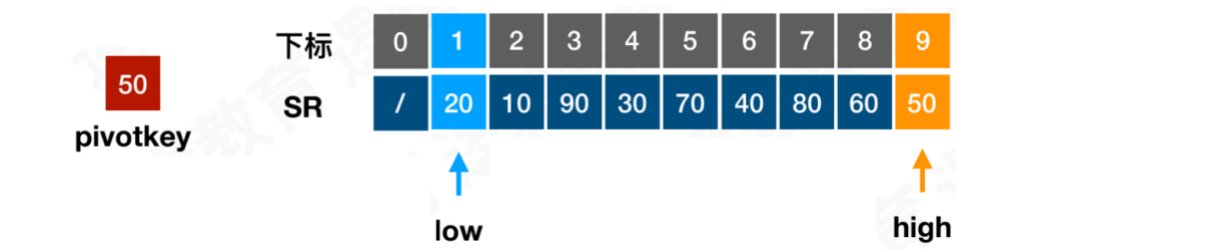
image.png

⽤低位low的元素与pivotkey进⾏⽐较找到⽐枢轴⼤的记录，交换到⾼端位置上

判断依据：_arr[low] >= pivotkey && low < high循环则继续往下查找，low += 1向后移动

此时_arr[1] = 20，pivotkey = 50，_arr[low] < pivotkey，则low += 1，low = 2
image.png

继续向后对比，此时_arr[2] = 10，pivotkey = 50，_arr[low] < pivotkey，则low += 1，low = 3
image.png

此时_arr[3] > 50，则循环退出，退出后交换low与high位置的元素
image.png

判断low < high，此时low = 3，high = 9，满⾜循环条件，继续进行对比

按照上述逻辑，当low与high相遇时，以枢轴作为中心点，左子表中的元素都比枢轴小，而右子表中的元素都比枢轴大
image.png

当low == high退出循环，表示这⼀次从两端交替向中间的扫描已经全部完成

此时low值为5，接下来按照同样的逻辑来对左子表与右子表进⾏同样的操作，以枢轴为中心点，左子表的范围是[1, 5 - 1]，右子表的范围是[5 + 1, 9]
image.png

2.2 代码实现

计算枢轴位置：

class Sort<Element : Comparable> {

    // 计算枢轴位置
    fileprivate func partition(low: Int, hight: Int) -> Int {

        var _low = low;
        var _hight = hight;
        // 默认将第一个元素作为枢轴的值
        let pivotKey = _arr[_low]!;

        // 低位与高位相遇，退出循环
        while(_low < _hight) {

            // 低位与高位不能相遇，并且高位数据大于等于枢轴
            while(_low < _hight && _arr[_hight]! >= pivotKey){
                // 高位向前移动
                _hight -= 1;
            }

            // 将小于枢轴的元素交换到低位
            swap(i: _low, j: _hight);

            // 低位与高位不能相遇，并且低位数据小于等于枢轴
            while(_low < _hight && _arr[_low]! <= pivotKey){
                // 低位向前移动
                _low += 1;
            }

            // 将大于枢轴的元素交换到高位
            swap(i: _low, j: _hight);
        }

        // 返回最终的枢轴位置，它之前的元素一定小于等于枢轴值，它之后的元素一定大于等于枢轴值
        return _low;
    }
}

  • 选取当中⼀个关键字作为枢轴

  • 将它放在⼀个合适的位置上，使得它的左边的值都它⼩，右边的值都⽐它⼤

子表排序方法：

class Sort<Element : Comparable> {

    // 子表排序方法
    fileprivate func QSort(low: Int, hight: Int) {

        // 判断低位与高位不能相遇，否则结束递归
        if(low >= hight){
            return;
        }

        // 计算枢轴位置
        let pivot = partition(low: low, hight: hight);
        // 将【低位 ~ 枢轴 - 1】范围作为左子表，对其进行排序
        QSort(low: low, hight: pivot - 1);
        // 将【枢轴 + 1 ~ 高位】范围作为右子表，对其进行排序
        QSort(low: pivot + 1, hight: hight);
    }
}

  • 判断low是否⼩于high

  • 求得枢轴，并且将数组枢轴左边的关键字都⽐它⼩，右边的关键字都⽐枢轴对应的关键字⼤

  • 将数组⼀分为⼆，对低⼦表进⾏排序，对⾼⼦表进⾏排序

快速排序：

class Sort<Element : Comparable> {

    // 快速排序
    func quickSort(){
        // 低位指针默认为序列起始位置
        let low = 1;
        // 高位指针默认为序列结束位置
        let hight = _arr.count - 1;
        // 将序列看做一张子表，调用子表排序方法
        QSort(low: low, hight: hight);
    }
}
  • 将序列看做一张子表，低位与高位分别为序列起始位置和结束位置，调用子表排序方法

partition函数时间复杂度，最好的情况：O(nlogn)

  • T(n) <= 2T(n / 2) + n，T(1) = 0

  • T(n) <= 2(2T(n / 4) + n / 2) + n = 4T(n / 4) + 2n

  • T(n) <= 4(2T(n / 8) + n / 4) + 2n = 8T(n / 8) + 3n

  • T(n) <= nT(1) + log2n * n = O(nlogn)

partition函数时间复杂度，最坏的情况：O(n ^ 2)

  • 排序的序列刚好是逆向和正序，那么递归树需要递归n - 1次，且在第i次划分需要经过n - i次关键字⽐较才找到⽐第i个记录，也就枢轴的位置

  • 那么⽐较的次数：(n - 1) + (n - 2) + (n - 3) ... + 1 = (n(n - 1)) / 2

空间复杂度：取决于递归造成的栈空间

  • 最好的情况下，递归树的深度为log2n，那么其空间复杂度为O(logn)

  • 最坏的情况下，需要进⾏n - 1次递归调⽤，那么其空间复杂度为O(n)

  • 平均情况下空间复杂度为O(logn)

2.3 优化分析

【优化一】枢轴的选择

上面的算法中，我们默认将第一个元素作为枢轴的值，这是一个较为暴力的做法

例如：以下序列，我们选择9作为枢轴的值
image.png

由于9是序列中的最大值，会被交换到序列尾部，剩余元素依次与9对比，最终得到的左子表范围是[1, 8]，所有这一轮的循环计算并没有什么意义
image.png

故此，枢轴的选择是优化方案的关键，一般会有两种做法：

  • 使用一个随机位置作为枢轴，完全看运气

  • 选择低、中、高三个位置的元素，取三个元素的中间值作为枢轴，这样避免枢轴成为序列中的最大值或最小值。通过这种方式选择的枢轴，它不一定是最合适的，但一个不会是最不合适的

【优化二】元素的交换

在寻找枢轴位置的时候，我们一直使用枢轴与低位或高位元素进行反复交换

实际上我们可以将枢轴的值存储在_arr[0]位置。在枢轴与低位或高位的元素对比时，遇到不符合规则的元素，直接将该元素替换到当前枢轴的位置上即可
image.png

而替换后的序列为：
image.png

当low与high相遇时，我们已经求得枢轴的位置
image.png

最后将存储在_arr[0]中枢轴的值，替换到该位置上
image.png

经过第一轮的枢轴选择，最终得到的序列为：
image.png

代码实现：

class Sort<Element : Comparable> {

    // 计算枢轴位置
    fileprivate func partition(low: Int, hight: Int) -> Int {

        var _low = low;
        var _hight = hight;
        // 计算中位的索引值
        let _middle = (_low + _hight) / 2;

        // 低位与高位元素比较，将较大值交换到高位
        if(_arr[_low]! > _arr[_hight]!){
            swap(i: _low, j: _hight);
        }

        // 中位与高位元素比较，将较大值交换到高位
        if(_arr[_middle]! > _arr[_hight]!){
            swap(i: _middle, j: _hight);
        }

        // 低位与中位元素比较，将较大值交换到低位
        if(_arr[_low]! < _arr[_middle]!){
            swap(i: _low, j: _middle);
        }

        // 此时低位是低、中、高三个元素中的中间值，将其赋值到位置0
        _arr[0] = _arr[_low]!;

        // 低位与高位相遇，退出循环
        while(_low < _hight) {

            // 低位与高位不能相遇，并且高位数据大于等于枢轴
            while(_low < _hight && _arr[_hight]! >= _arr[0]!){
                // 高位向前移动
                _hight -= 1;
            }

            // 将小于枢轴的高位值，替换到低位
            _arr[_low] = _arr[_hight];

            // 低位与高位不能相遇，并且低位数据小于等于枢轴
            while(_low < _hight && _arr[_low]! <= _arr[0]!){
                // 低位向前移动
                _low += 1;
            }

            // 将大于枢轴的低位值，替换到高位
            _arr[_hight] = _arr[_low];
        }

        // 将枢轴值，替换到真正的枢轴位置上
        _arr[_low] = _arr[0];

        // 返回最终的枢轴位置，它之前的元素一定小于等于枢轴值，它之后的元素一定大于等于枢轴值
        return _low;
    }
}

3. 排序类别汇总

插入排序类：

  • 直接插入排序

  • 希尔排序

选择排序类：

  • 简单选择排序

  • 堆排序

交换排序类：

  • 冒泡排序

  • 快速排序

归并排序类：

  • 归并排序

排序算法时间复杂度与空间复杂度汇总：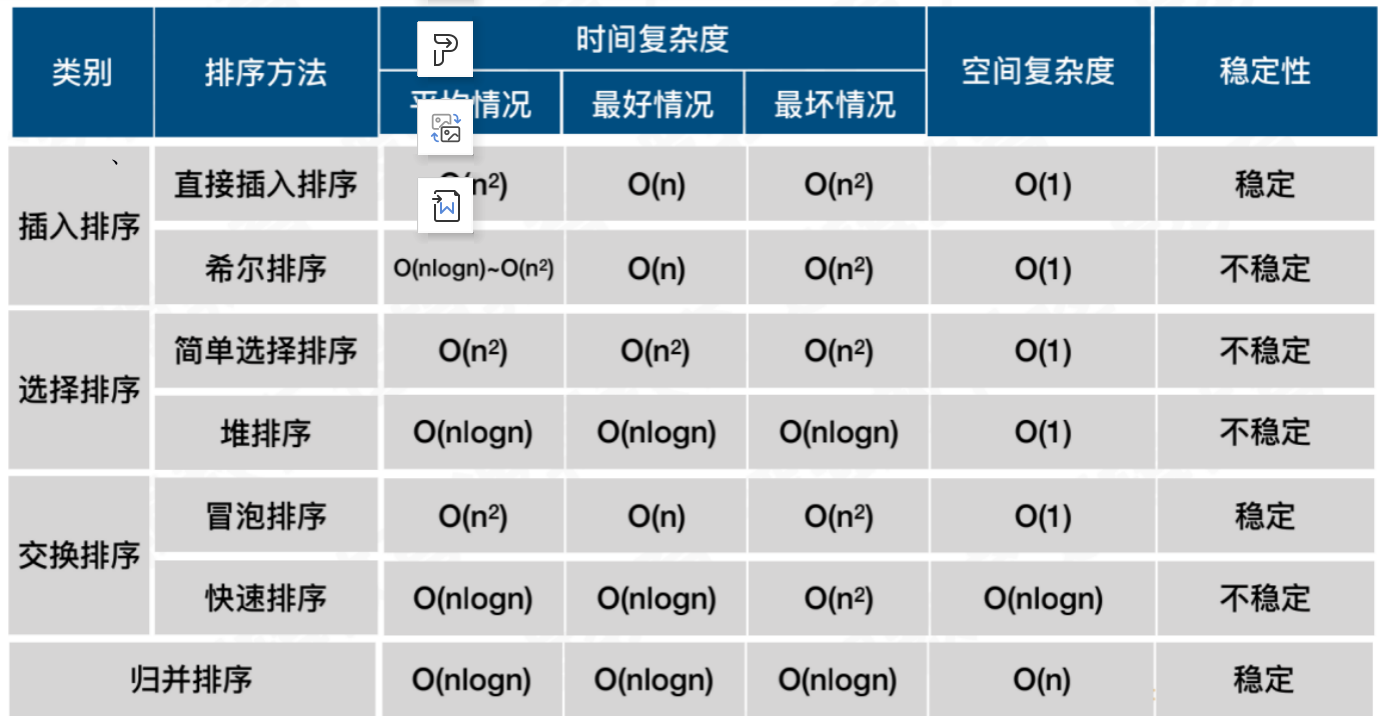
image.png

总结

归并排序（Merging Sort）：

  • 就是利⽤归并的思想实现排序⽅法。它的原理是假设初始序列含有n个记录，则可以看成n个有序的⼦序列，每个⼦序列的⻓度为1，然后两两合并。得到n / 2个⻓度为2或1的有序⼦序列，再两两归并。如此重复，直到得到⼀个⻓度为n的有序序列为止，这种排序⽅法称为2路归并排序

  • 算法分为两个步骤：

    • 【步骤一】拆解：将数组中的元素，按照2倍规则拆解成的独立⼦序列

    • 【步骤二】归并：将⼦序列两两合并，合并过程中同时排序，使其合并后变为有序

快速排序（Quick Sort）：

  • 基本思想：通过⼀趟排序将待排序记录分割成独⽴的两部分。其中⼀部分记录的关键字均为另⼀部分记录的关键字⼩，则可分别对两部分记录继续进⾏排序，以达到整个序列有序的⽬的

  • 算法分为两个步骤：

    • 对子表进行排序

      • 判断low是否⼩于high

      • 求得枢轴，并且将数组枢轴左边的关键字都⽐它⼩，右边的关键字都⽐枢轴对应的关键字⼤

      • 将数组⼀分为⼆，对低⼦表进⾏排序，对⾼⼦表进⾏排序

    • 求解枢轴

      • 选取当中⼀个关键字作为枢轴

      • 将它放在⼀个合适的位置上，使得它的左边的值都它⼩，右边的值都⽐它⼤