1. 最短路径问题
最短路径就是求解,从源点到终点之间,所经过权值最小的路线
例如:求解V0至V8所经过的最短路径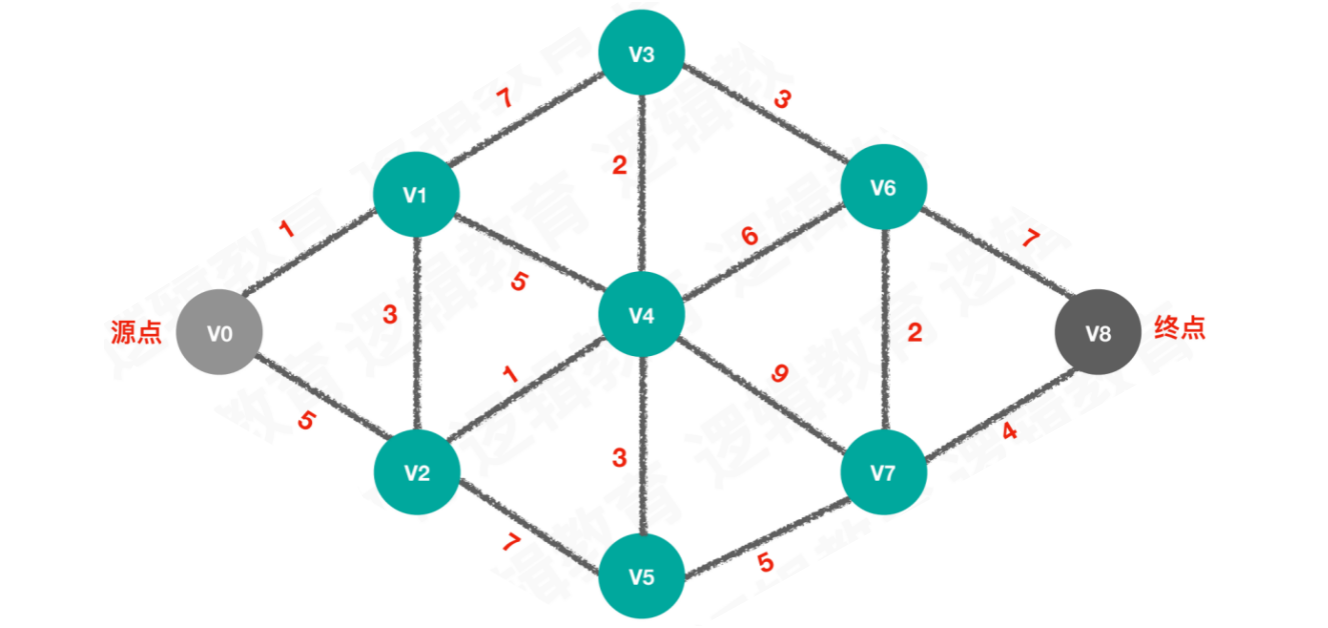
图中源点V0到达终点V8的路径不止一条,我们要找出一条路径,使得沿此路径上各边的权值总和达到最小
较为常用的求解算法有两种:
迪克斯特拉(
Dijkstra)算法弗洛伊德(
Floyd)算法
2. 迪克斯特拉(Dijkstra)算法
Dijkstra算法特点:从源点开始,采用贪心算法的策略,每次遍历到始点距离最近且未访问过的顶点的邻接结点,直到扩展到终点为止
【步骤一】从源点V0出发,待选择的路线为1和5,优先选择权值更小的路线1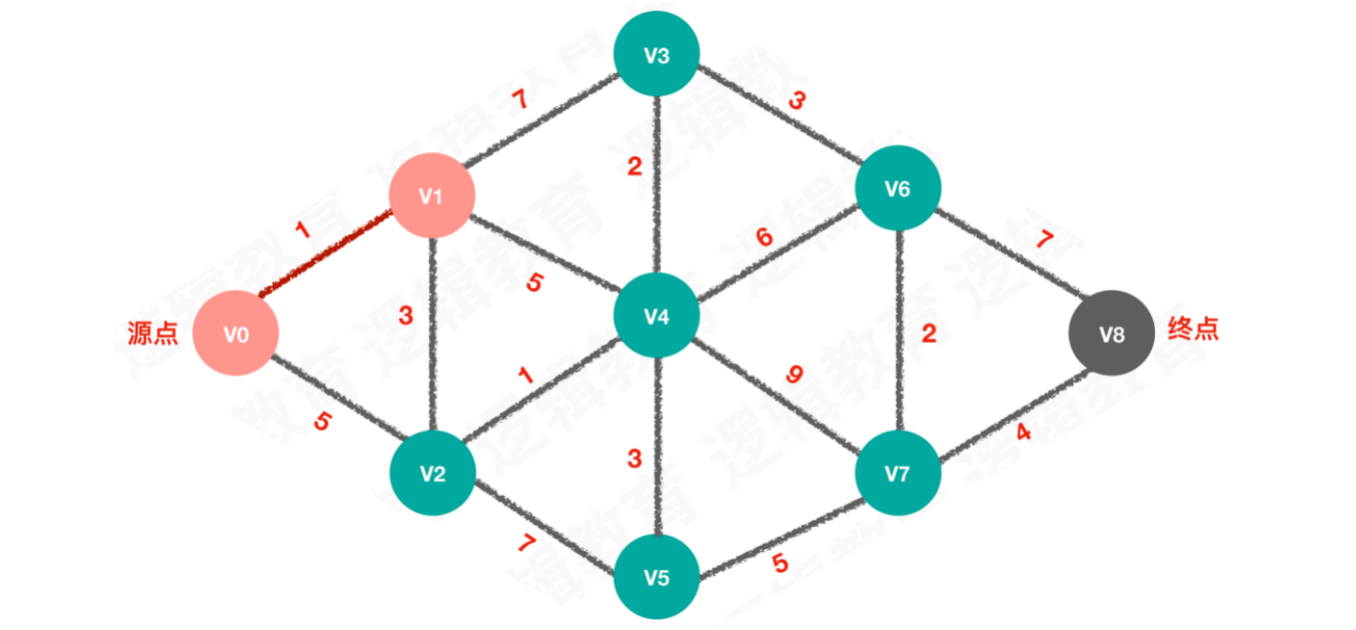
【步骤二】待选择的路线为3、5、7,选择路线3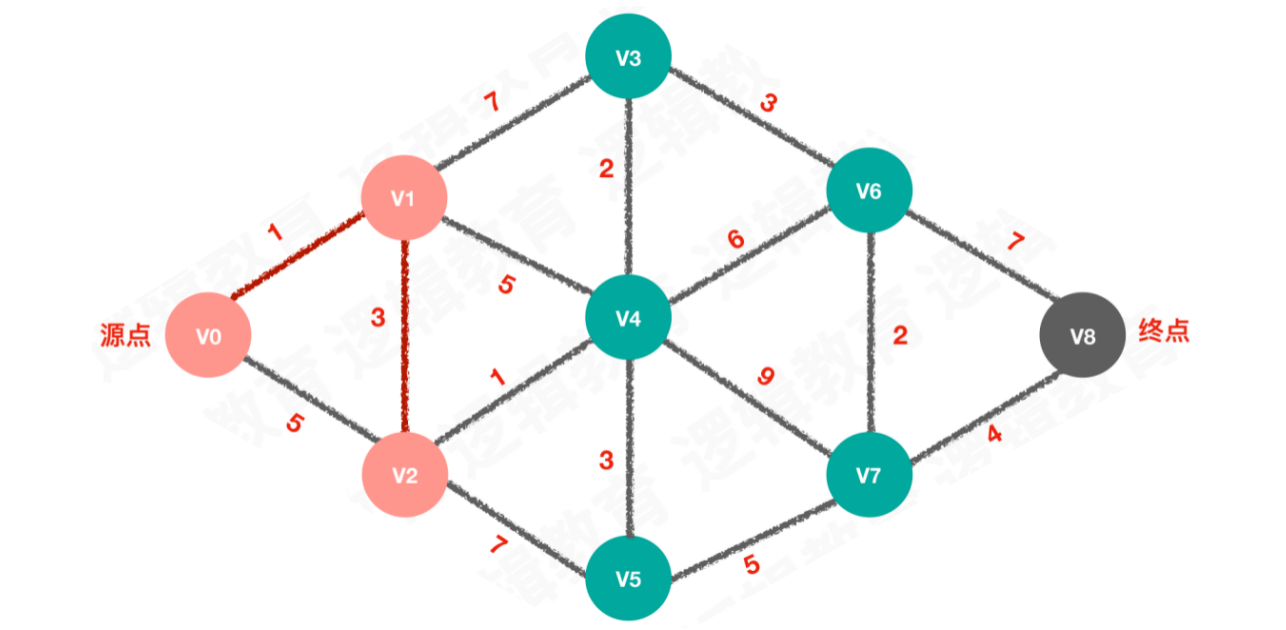
【步骤三】待选择的路线为1、7,选择路线1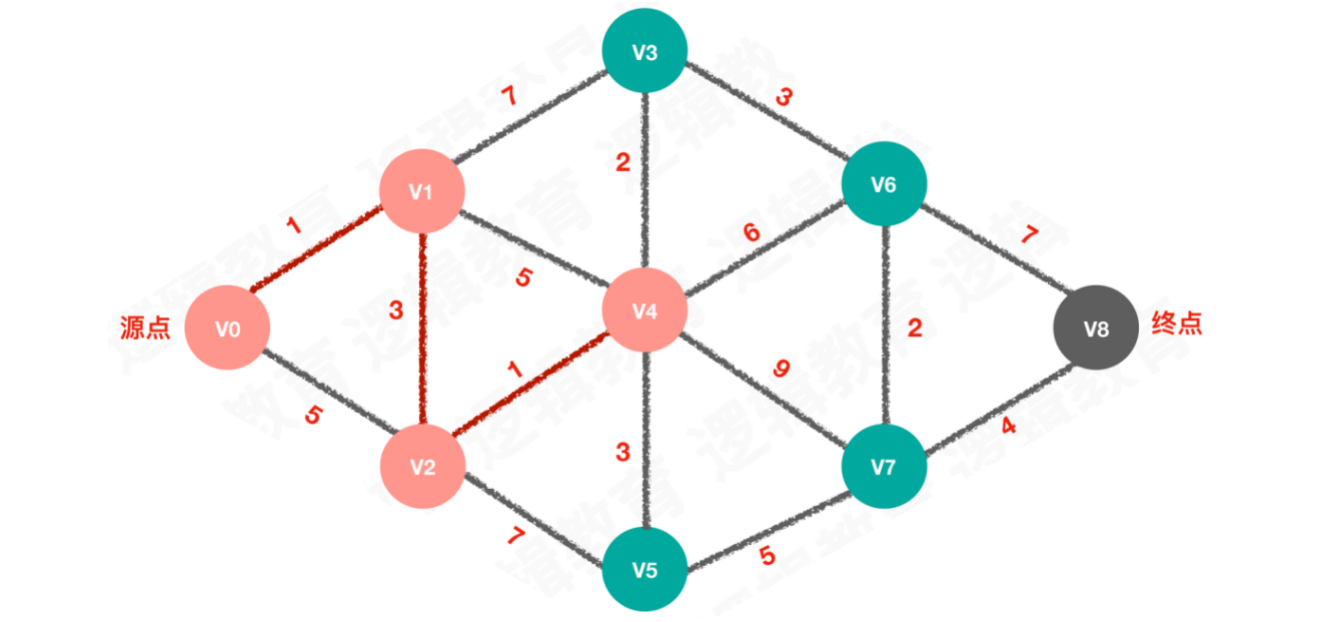
【步骤四】待选择的路线为2、6、9、3,选择路线2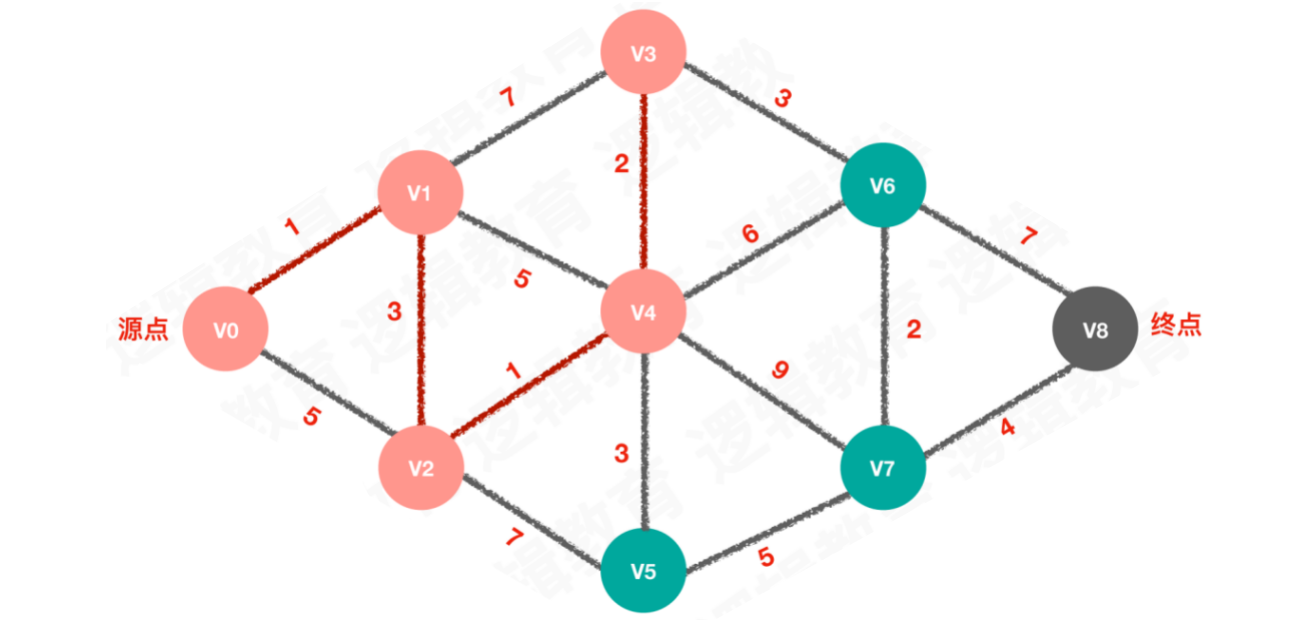
【步骤五】待选择的路线为3,选择路线3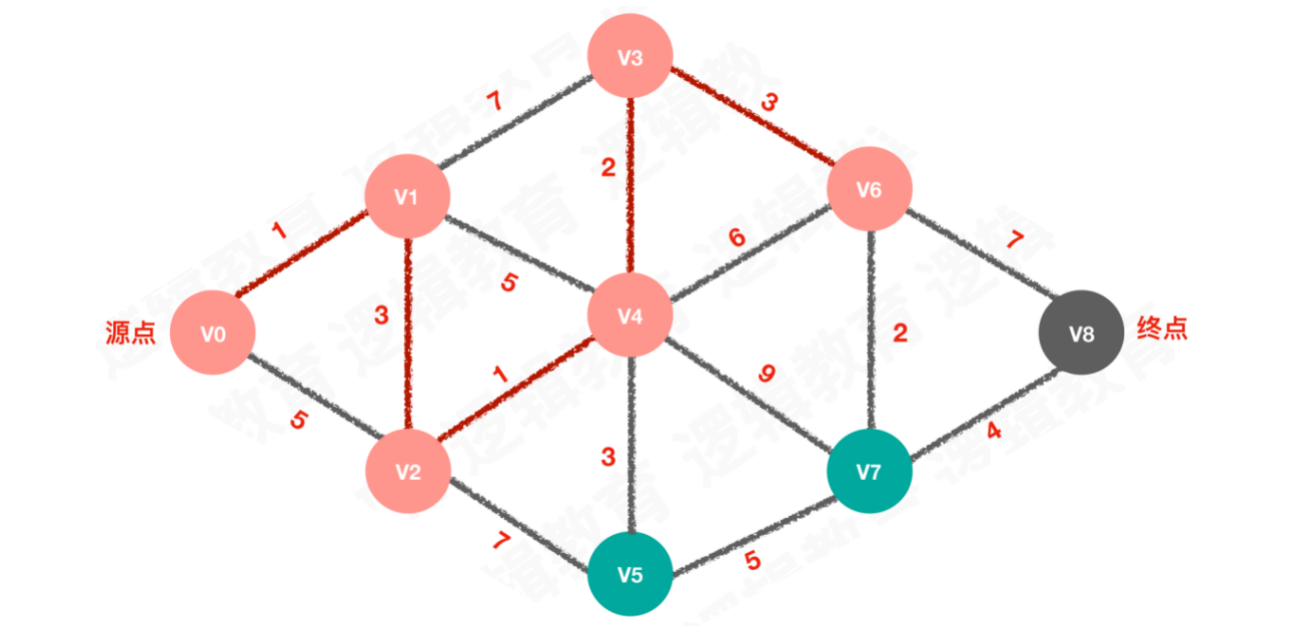
【步骤六】待选择的路线为2、7,选择路线2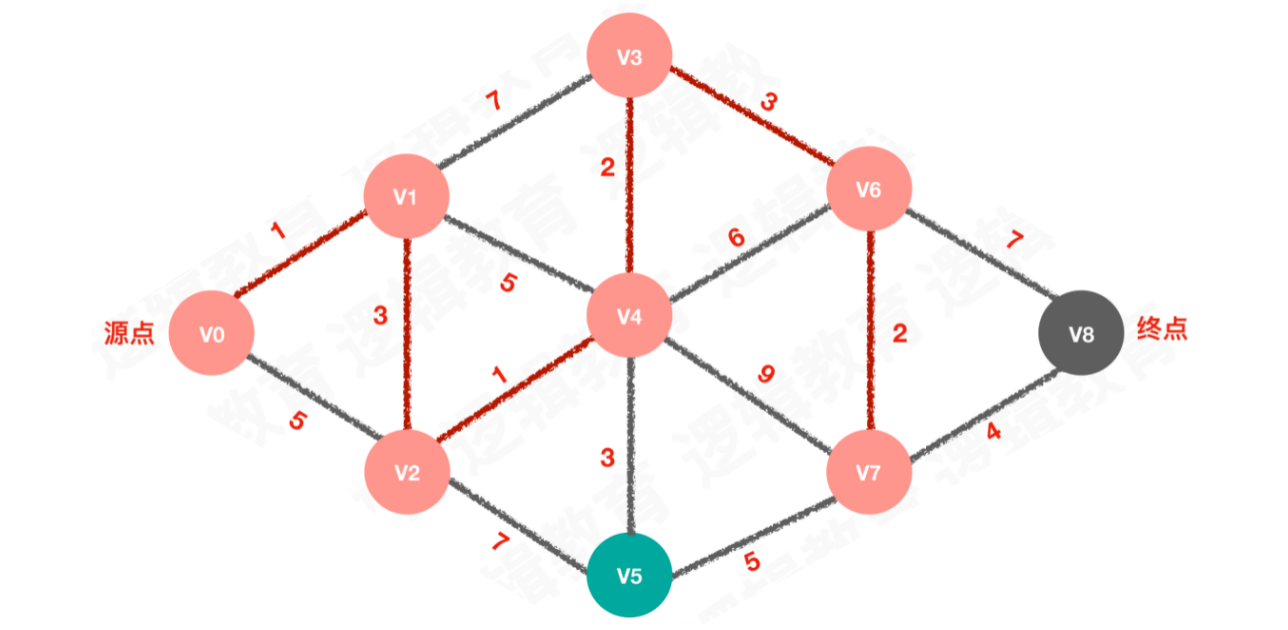
【步骤七】待选择的路线为4,选择路线4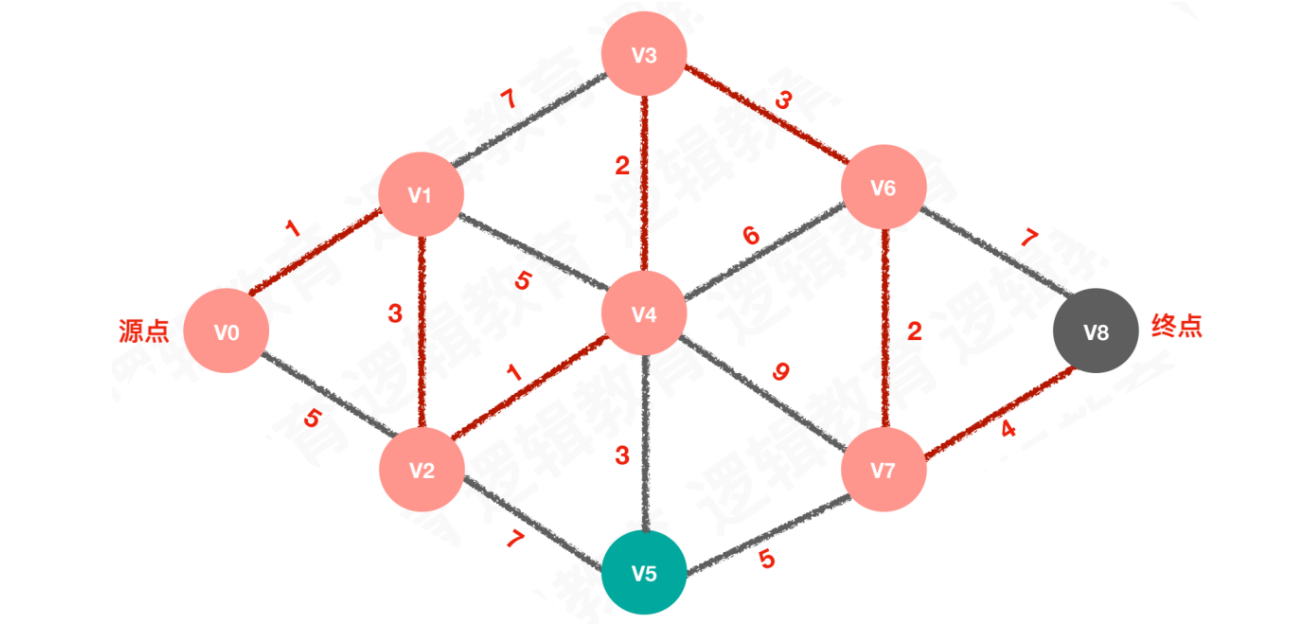
最短路径:V0 → V1 → V2 → V4 → V3 → V6 → V7 → V8
最短路径权值总和:1 + 3 + 1 + 2 + 3 + 2 + 4 = 16
2.1 算法思路
final数组:表示V0到某个顶点Vw是否已经求得了最短路径的标记。如果V0到Vw已经有结果,则final[w] = 1D数组:表示V0到某个顶点Vw的路径p数组:当前顶点的前驱顶点的下标
2.2 算法分析
首先将网图使用邻接矩阵存储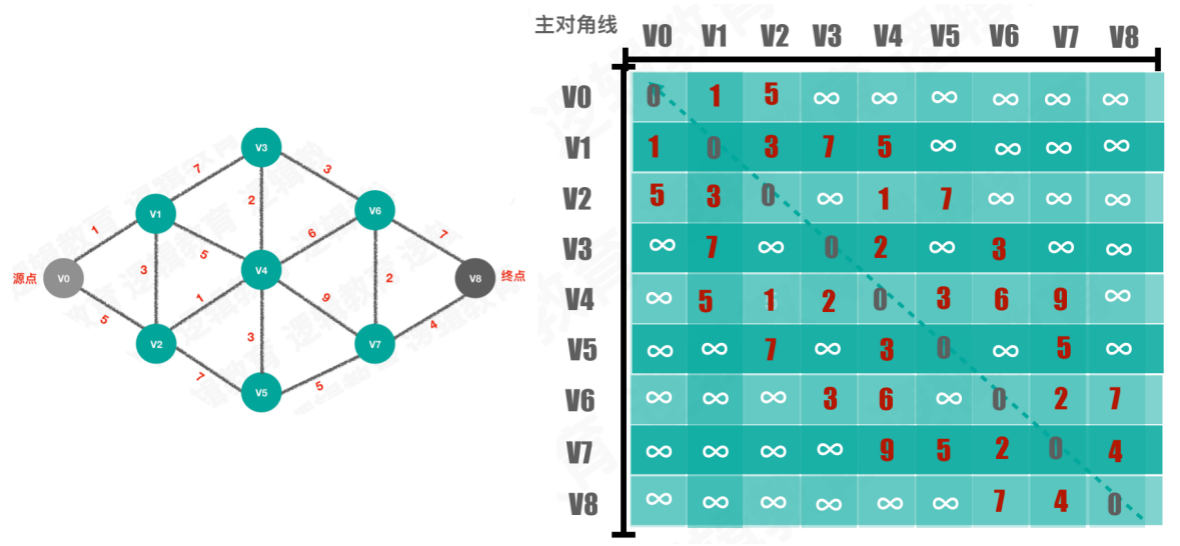
【初始化】从源点V0开始,至终点V8结束
beginIndex = 0endIndex = 8
初始化三个数组,并更新源点V0的初始数据
final = [1, 0, 0, 0, 0, 0, 0, 0, 0]
D = [0, 1, 5, max, max, max, max, max, max]
p = [-1, 0, 0, 0, 0, 0, 0, 0, 0]
final中,默认使用0填充- 将索引
0的位置标记为1,表示已求得V0的最短路径
- 将索引
D数组中,默认使用Int.max填充,并更新V0到其他顶点的权值将索引
0的位置标记为0,表示V0 → V0将索引
1和2的位置,更新为V0到V1和V2所需的权值
p数组中,默认使用0填充将索引
0的位置标记为-1,表示V0没有前驱顶点将索引
1和2的位置更新为0,表示V0是它们的前驱顶点
【第一次执行】以V0为起始点,遍历数组D,满足final[i] == 0,表示当前顶点未求得最短路径。找到符合条件并且权值最小的1,将其对应的索引值赋值给k,权值赋值给min,并更新final[1] = 1
k = 1
min = 1
final = [1, 1, 0, 0, 0, 0, 0, 0, 0]
遍历final,满足final[w] == 0,表示w位置还未得到最短路径。同时符合min + G.arc[k][w] < D[w]的逻辑,表示V0 → Vw的权值比之前D[w]更小,则数组D和数组p更新
当
w = 0、1,final[w] == 1,条件不满足当
w = 2,final[2] == 0,min + arc[1][2] < D[2]→1 + 3 < 5,条件成立。即V0 → V1 → V2比V0 → V2路径更短,更新数组D和数组p:// D[w] = min + G.arc[k][w] → D[2] = 1 + 3 = 4 D = [0, 1, 4, max, max, max, max, max, max] // p[w] = k → p[2] = 1 p = [-1, 0, 1, 0, 0, 0, 0, 0, 0]当
w = 3,final[3] == 0,min + arc[1][3] < D[3]→1 + 7 < max,条件成立。即求得V0 → V1 → V3最短路径的权值,更新数组D和数组p:// D[w] = min + G.arc[k][w] → D[3] = 1 + 7 = 8 D = [0, 1, 4, 8, max, max, max, max, max] // p[w] = k → p[3] = 1 p = [-1, 0, 1, 1, 0, 0, 0, 0, 0]当
w = 4,final[4] == 0,min + arc[1][4] < D[4]→1 + 5 < max,条件成立。即求得V0 → V1 → V4最短路径的权值,更新数组D和数组p:// D[w] = min + G.arc[k][w] → D[4] = 1 + 5 = 6 D = [0, 1, 4, 8, 6, max, max, max, max] // p[w] = k → p[4] = 1 p = [-1, 0, 1, 1, 1, 0, 0, 0, 0]当
w = 5,final[5] == 0,min + arc[1][5] < D[5]→1 + max < max,条件不成⽴当
w = 6,final[6] == 0,min + arc[1][6] < D[6]→1 + max < max,条件不成⽴当
w = 7,final[7] == 0,min + arc[1][7] < D[7]→1 + max < max,条件不成⽴当
w = 8,final[8] == 0,min + arc[1][8] < D[8]→1 + max < max,条件不成⽴
第一次的执行结果为:
final = [1, 1, 0, 0, 0, 0, 0, 0, 0]
D = [0, 1, 4, 8, 6, max, max, max, max]
p = [-1, 0, 1, 1, 1, 0, 0, 0, 0]
【第二次执行】以V1为起始点,遍历数组D,找到符合条件并且权值最小的4,将其对应的索引值赋值给k,权值赋值给min,并更新final[2] = 1
k = 2
min = 4
final = [1, 1, 1, 0, 0, 0, 0, 0, 0]
遍历final:
当
w = 0、1、2,final[w] == 1,条件不满足当
w = 3,final[3] == 0,min + arc[2][3] < D[3]→4 + max < 8,条件不成⽴当
w = 4,final[4] == 0,min + arc[2][4] < D[4]→4 + 1 < 6,条件成立。即V1 → V2 → V4比V1 → V4路径更短,更新数组D和数组p:// D[w] = min + G.arc[k][w] → D[4] = 4 + 1 = 5 D = [0, 1, 4, 8, 5, max, max, max, max] // p[w] = k → p[4] = 2 p = [-1, 0, 1, 1, 2, 0, 0, 0, 0]当
w = 5,final[5] == 0,min + arc[2][5] < D[5]→4 + 7 < max,条件成立。即求得V1 → V2 → V5最短路径的权值,更新数组D和数组p:// D[w] = min + G.arc[k][w] → D[5] = 4 + 7 = 11 D = [0, 1, 4, 8, 5, 11, max, max, max] // p[w] = k → p[5] = 2 p = [-1, 0, 1, 1, 2, 2, 0, 0, 0]当
w = 6,final[6] == 0,min + arc[2][6] < D[6]→4 + max < max,条件不成⽴当
w = 7,final[7] == 0,min + arc[2][7] < D[7]→4 + max < max,条件不成⽴当
w = 8,final[8] == 0,min + arc[2][8] < D[8]→4 + max < max,条件不成⽴
第二次的执行结果为:
final = [1, 1, 1, 0, 0, 0, 0, 0, 0]
D = [0, 1, 4, 8, 5, 11, max, max, max]
p = [-1, 0, 1, 1, 2, 2, 0, 0, 0]
【第三次执行】以V2为起始点,遍历数组D,找到符合条件并且权值最小的5,将其对应的索引值赋值给k,权值赋值给min,并更新final[4] = 1
k = 4
min = 5
final = [1, 1, 1, 0, 1, 0, 0, 0, 0]
遍历final:
当
w = 0、1、2、4,final[w] == 1,条件不满足当
w = 3,final[3] == 0,min + arc[4][3] < D[3]→5 + 2 < 8,条件成立。即V2 → V4 → V3比V1 → V3路径更短,更新数组D和数组p:// D[w] = min + G.arc[k][w] → D[3] = 5 + 2 = 7 D = [0, 1, 4, 7, 5, 11, max, max, max] // p[w] = k → p[3] = 4 p = [-1, 0, 1, 4, 2, 2, 0, 0, 0]当
w = 5,final[5] == 0,min + arc[4][5] < D[5]→5 + 3 < 11,条件成立。即V2 → V4 → V5比V2 → V5路径更短,更新数组D和数组p:// D[w] = min + G.arc[k][w] → D[5] = 5 + 3 = 8 D = [0, 1, 4, 7, 5, 8, max, max, max] // p[w] = k → p[5] = 4 p = [-1, 0, 1, 4, 2, 4, 0, 0, 0]当
w = 6,final[6] == 0,min + arc[4][6] < D[6]→5 + 6 < max,条件成立。即求得... → V2 → V4 → V6最短路径的权值,更新数组D和数组p:// D[w] = min + G.arc[k][w] → D[6] = 5 + 6 = 11 D = [0, 1, 4, 7, 5, 8, 11, max, max] // p[w] = k → p[6] = 4 p = [-1, 0, 1, 4, 2, 4, 4, 0, 0]当
w = 7,final[7] == 0,min + arc[4][7] < D[7]→5 + 9 < max,条件成立。即求得... → V2 → V4 → V7最短路径的权值,更新数组D和数组p:// D[w] = min + G.arc[k][w] → D[7] = 5 + 9 = 14 D = [0, 1, 4, 7, 5, 8, 11, 14, max] // p[w] = k → p[7] = 4 p = [-1, 0, 1, 4, 2, 4, 4, 4, 0]当
w = 8,final[8] == 0,min + arc[4][8] < D[8]→5 + max < max,条件不成立
第三次的执行结果为:
final = [1, 1, 1, 0, 1, 0, 0, 0, 0]
D = [0, 1, 4, 7, 5, 8, 11, 14, max]
p = [-1, 0, 1, 4, 2, 4, 4, 4, 0]
【第四次执行】以V4为起始点,遍历数组D,找到符合条件并且权值最小的7,将其对应的索引值赋值给k,权值赋值给min,并更新final[3] = 1
k = 3
min = 7
final = [1, 1, 1, 1, 1, 0, 0, 0, 0]
遍历final:
当
w = 0、1、2、3、4,final[0] == 1,条件不满足当
w = 5,final[5] == 0,min + arc[3][5] < D[5]→7 + max < 8,条件不成立当
w = 6,final[6] == 0,min + arc[3][6] < D[6]→7 + 3 < 11,条件成立。即V4 → V3 → V6比V4 → V6路径更短,更新数组D和数组p:// D[w] = min + G.arc[k][w] → D[6] = 7 + 3 = 10 D = [0, 1, 4, 7, 5, 8, 10, 14, max] // p[w] = k → p[6] = 3 p = [-1, 0, 1, 4, 2, 4, 3, 4, 0]当
w = 7,final[7] == 0,min + arc[3][7] < D[7]→7 + max < 14,条件不成立当
w = 8,final[8] == 0,min + arc[3][8] < D[8]→7 + max < max,条件不成立
第四次的执行结果为:
final = [1, 1, 1, 1, 1, 0, 0, 0, 0]
D = [0, 1, 4, 7, 5, 8, 10, 14, max]
p = [-1, 0, 1, 4, 2, 4, 3, 4, 0]
【第五次执行】以V3为起始点,遍历数组D,找到符合条件并且权值最小的8,将其对应的索引值赋值给k,权值赋值给min,并更新final[5] = 1
k = 5
min = 8
final = [1, 1, 1, 1, 1, 1, 0, 0, 0]
遍历final:
当
w = 0、1、2、3、4、5,final[w] == 1,条件不满足当
w = 6,final[6] == 0,min + arc[5][6] < D[6]→8 + max < 10,条件不成立当
w = 7,final[7] == 0,min + arc[5][7] < D[7]→8 + 5 < 14,条件成立。即V4 → V5 → V7比V4 → V7路径更短,更新数组D和数组p:// D[w] = min + G.arc[k][w] → D[6] = 8 + 5 = 13 D = [0, 1, 4, 7, 5, 8, 10, 13, max] // p[w] = k → p[6] = 5 p = [-1, 0, 1, 4, 2, 4, 3, 5, 0]当
w = 8,final[8] == 0,min + arc[5][8] < D[8]→8 + max < max,条件不成立
第五次的执行结果为:
final = [1, 1, 1, 1, 1, 1, 0, 0, 0]
D = [0, 1, 4, 7, 5, 8, 10, 13, max]
p = [-1, 0, 1, 4, 2, 4, 3, 5, 0]
【第六次执行】以V5为起始点,遍历数组D,找到符合条件并且权值最小的10,将其对应的索引值赋值给k,权值赋值给min,并更新final[6] = 1
k = 6
min = 10
final = [1, 1, 1, 1, 1, 1, 1, 0, 0]
遍历final:
当
w = 0、1、2、3、4、5、6,final[w] == 1,条件不满足当
w = 7,final[7] == 0,min + arc[6][7] < D[7]→10 + 2 < 13,条件成立。即V3 → V6 → V7比V5 → V7路径更短,更新数组D和数组p:// D[w] = min + G.arc[k][w] → D[7] = 10 + 2 = 12 D = [0, 1, 4, 7, 5, 8, 10, 12, max] // p[w] = k → p[7] = 6 p = [-1, 0, 1, 4, 2, 4, 3, 6, 0]当
w = 8,final[8] == 0,min + arc[6][8] < D[8]→10 + 7 < max,条件成立。即求得... → V3 → V6 → V8最短路径的权值,更新数组D和数组p:// D[w] = min + G.arc[k][w] → D[8] = 10 + 7 = 17 D = [0, 1, 4, 7, 5, 8, 10, 12, 17] // p[w] = k → p[8] = 6 p = [-1, 0, 1, 4, 2, 4, 3, 6, 6]
第六次的执行结果为:
final = [1, 1, 1, 1, 1, 1, 1, 0, 0]
D = [0, 1, 4, 7, 5, 8, 10, 12, 17]
p = [-1, 0, 1, 4, 2, 4, 3, 6, 6]
【第七次执行】以V6为起始点,遍历数组D,找到符合条件并且权值最小的12,将其对应的索引值赋值给k,权值赋值给min,并更新final[7] = 1
k = 7
min = 12
final = [1, 1, 1, 1, 1, 1, 1, 1, 0]
遍历final:
当
w = 0、1、2、3、4、5、6、7,final[w] == 1,条件不满足当
w = 8,final[8] == 0,min + arc[7][8] < D[8]→12 + 4 < 17,条件满足。即V6 → V7 → V8比V6 → V8路径更短,更新数组D和数组p:// D[w] = min + G.arc[k][w] → D[8] = 12 + 4 = 16 D = [0, 1, 4, 7, 5, 8, 10, 12, 16] // p[w] = k → p[8] = 7 p = [-1, 0, 1, 4, 2, 4, 3, 6, 7]
第七次的执行结果为:
final = [1, 1, 1, 1, 1, 1, 1, 1, 0]
D = [0, 1, 4, 7, 5, 8, 10, 12, 16]
p = [-1, 0, 1, 4, 2, 4, 3, 6, 7]
【第八次执行】以V7为起始点,遍历数组D,找到符合条件并且权值最小的16,将其对应的索引值赋值给k,权值赋值给min,并更新final[8] = 1
k = 8
min = 16
final = [1, 1, 1, 1, 1, 1, 1, 1, 1]
第八次的执行结果为:
final = [1, 1, 1, 1, 1, 1, 1, 1, 1]
D = [0, 1, 4, 7, 5, 8, 10, 12, 16]
p = [-1, 0, 1, 4, 2, 4, 3, 6, 7]
此时,从源点V0到其他顶点,全部遍历结束
在
数组p中,存储了V0到其他顶点的最短路径。以终点V8为例:从索引8开始遍历,将对应的值作为前驱结点的索引,直到p[i] == -1停止,即可打印出从V0 → V8的整条路径在
数组D中,存储了V0到其他顶点最短路径所需的权值。以终点V8为例:打印D[8]即可得到V0 → V8最短路径所需的权值
2.3 代码实现
延用“邻接矩阵存储”的案例代码,修改MGraphLinear类中代码
class MGraphLinear {
var D : [Int]?;
var final : [Int]?;
var p : [Int]?;
func shortestPath_dijkstra(beginIndex : Int, endIndex : Int) -> String {
var str : String = "";
// 1、初始化三个数组
D = [Int].init(repeating: Int.max, count: self.graph.numNodes);
final = [Int].init(repeating: 0, count: self.graph.numNodes);
p = [Int].init(repeating: 0, count: self.graph.numNodes);
// 更新源点的初始数据
D![beginIndex] = 0;
final![beginIndex] = 1;
p![beginIndex] = -1;
// 更新源点所连接的顶点权值和前驱结点的索引值
for i in 0 ..< self.graph.numNodes{
let weight = self.graph.arc![beginIndex][i];
if(final![i] == 1 || weight == Int.max){
continue;
}
D![i] = weight;
p![i] = beginIndex;
}
// 2、遍历其他顶点,找到源点到各顶点的最短路径与所需权值
for _ in 1 ..< self.graph.numNodes{
var k = -1;
var min = Int.max;
// 3、从未求得最短路径的顶点中,找到最小权值
for i in 0 ..< self.graph.numNodes{
let weight = D![i];
if(final![i] == 1 || weight == Int.max){
continue;
}
if(weight < min){
// 将其对应的索引值赋值给k
k = i;
// 最小权值赋值给min
min = weight;
}
}
// 4、标记当前顶点已求得最短路径
final![k] = 1;
// 5、遍历所有顶点,更新顶点k与各顶点的最短路径和所需权值
for w in 0 ..< self.graph.numNodes{
// 已求得最短路径的顶点,跳过
if(final![w] == 1){
continue;
}
// 获得顶点k与顶点w的权值
var weight = self.graph.arc![k][w];
// 没有连接关系的顶点,跳过
if(weight == Int.max){
continue;
}
// weight = 当前权值 + 最小权值
weight += min;
// pre = 顶点w现有最短路径所需权值
let pre = D![w];
// 如果当前计算出的权值 >= 现有最短路径所需权值,跳过
if(weight >= pre){
continue;
}
// 否则,更新最短路径所需权值
D![w] = weight;
// 更新前驱结点的索引,更新后最短路径会随之改变
p![w] = k;
}
}
// 6、全部顶点遍历完成,打印终点对应的最短路径和权值
str = "V\(endIndex)";
var val = p![endIndex];
while(val != -1){
str = "V\(val) -> \(str)";
val = p![val];
}
str = "最短路径:\(str)\n";
str += "权值总和:\(D![endIndex])";
return str;
}
}
按照示例中的网图逻辑,使用代码创建邻接矩阵,并打印Dijkstra算法的结果:
let nodes = ["V0", "V1", "V2", "V3", "V4", "V5", "V6", "V7", "V8"];
let edges = [[0, 1 ,1], [0, 2, 5],
[1, 2, 3], [1, 3, 7], [1, 4, 5],
[2, 4, 1], [2, 5, 7],
[3, 4, 2], [3, 6, 3],
[4, 5, 3], [4, 6, 6], [4, 7, 9],
[5, 7, 5],
[6, 7, 2], [6, 8, 7],
[7, 8, 4],];
let isUndirected = true;
let isNet = true;
let graphLinear = MGraphLinear();
graphLinear.create(nodes: nodes, edges: edges, isUndirected: isUndirected, isNet: isNet);
print(graphLinear.traverse());
print("\(graphLinear.shortestPath_dijkstra(beginIndex: 0, endIndex: 8))");
-------------------------
//输出以下内容:
0 1 5 ∞ ∞ ∞ ∞ ∞ ∞
1 0 3 7 5 ∞ ∞ ∞ ∞
5 3 0 ∞ 1 7 ∞ ∞ ∞
∞ 7 ∞ 0 2 ∞ 3 ∞ ∞
∞ 5 1 2 0 3 6 9 ∞
∞ ∞ 7 ∞ 3 0 ∞ 5 ∞
∞ ∞ ∞ 3 6 ∞ 0 2 7
∞ ∞ ∞ ∞ 9 5 2 0 4
∞ ∞ ∞ ∞ ∞ ∞ 7 4 0
最短路径:V0 -> V1 -> V2 -> V4 -> V3 -> V6 -> V7 -> V8
权值总和:16
3. 弗洛伊德(Floyd)算法
Floyd算法特点:一种利用动态规划的思想寻找给定的加权图中多源点之间最短路径的算法,又称之为插点法
案例:以下图结构有三个顶点,求解V1 → V2的最短路径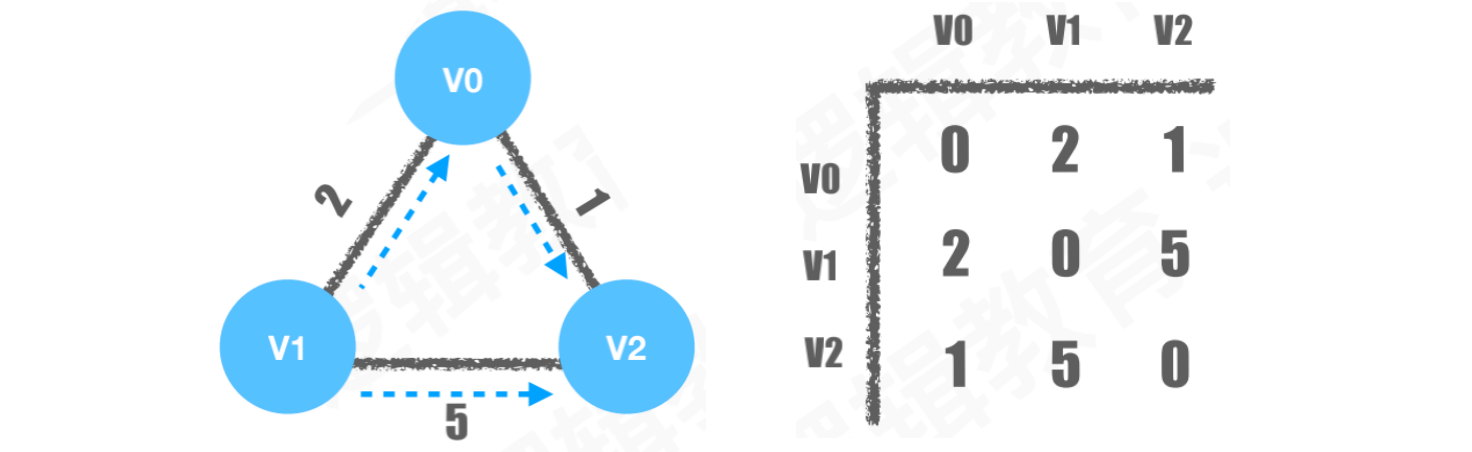
从V1到达V2有两条路径:
V1 → V2 = 5V1 → V0 → V2 = 3
创建两个二维数组进行辅助存储:
数组D:代表顶点到顶点的最短路径权值的矩阵数组p:代表对应顶点最短路径的前驱矩阵
由于D[1][2] > D[1][0] + D[0][2],所以修改D[1][2]和D[2][1]位置上的权值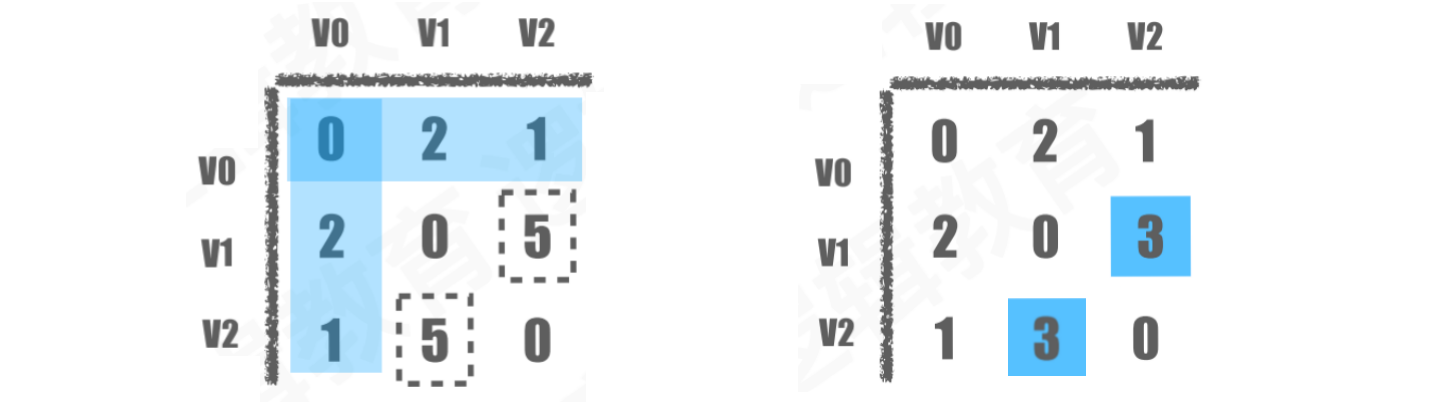
数组p默认使用p[i][j] = j初始化,当最短路径出现更优方案时,修改p[1][2]和p[2][1]位置上的前驱结点索引值,所以p[1][2] = p[1][0]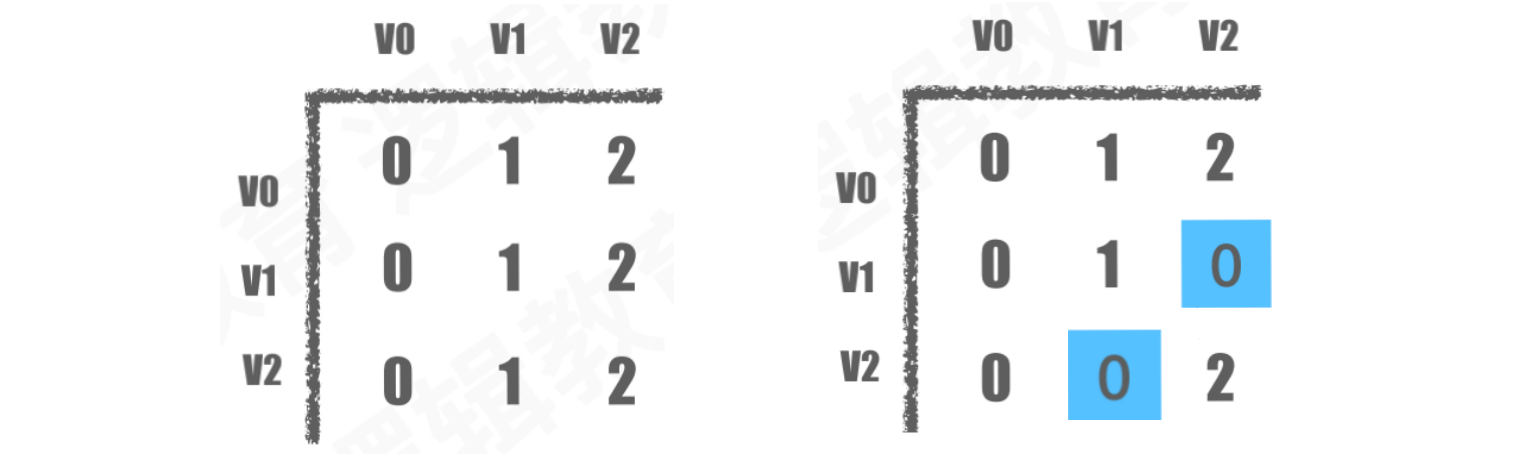
3.1 算法思路
数组D:代表顶点到顶点的最短路径权值的矩阵数组p:代表对应顶点最短路径的前驱矩阵公式:
D[v][w] = min{ D[v][w], D[v][k] + D[k][w] }k表示经过的中转顶点,变化从0 ~ nv表示邻接矩阵的横向索引位置,变化从0 ~ nw表示邻接矩阵的纵向索引位置,变化从0 ~ n使用该公式遍历最短路径,需要三重循环
示例代码:
【步骤一】初始化数组D与数组P矩阵
for(v = 0; v < G.numVertexes; ++v) {
for(w = 0; w < G.numVertexes; ++w) {
// D[v][w]值,即为对应点间的权值
(*D)[v][w] = G.arc[v][w];
// P[v][w] = w
(*P)[v][w] = w;
}
}
【步骤二】遍历最短路径
// K表示经过的中转顶点
for(k = 0; k < G.numVertexes; ++k) {
for(v = 0; v < G.numVertexes; ++v) {
for(w = 0; w < G.numVertexes; ++w) {
// 如果经过下标为k顶点路径⽐原两点间路径更短
if ((*D)[v][w] > (*D)[v][k] + (*D)[k][w]) {
// 将当前两点间权值设为更⼩的⼀个
(*D)[v][w] = (*D)[v][k] + (*D)[k][w];
// 路径设置为经过下标为k的顶点
(*P)[v][w] = (*P)[v][k];
}
}
}
}
3.2 算法分析
以此图为例: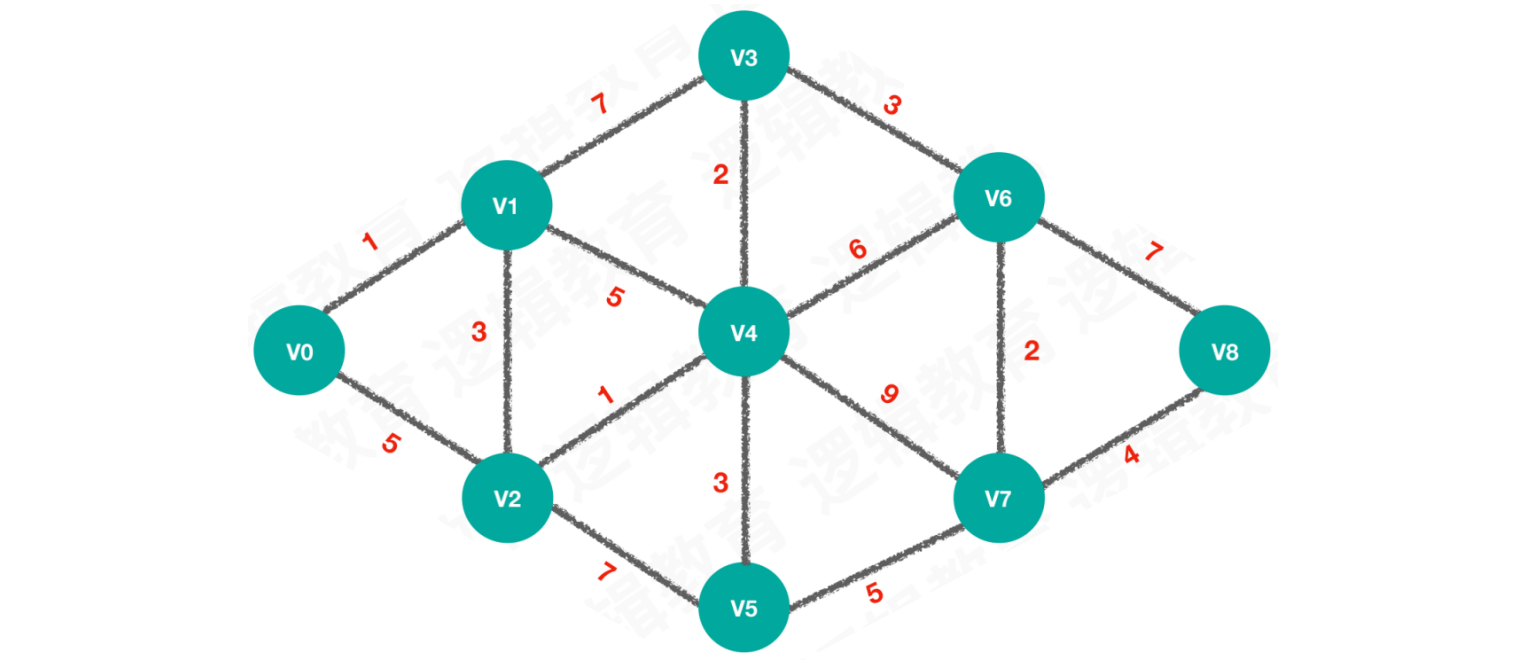
【初始化】将数组D按照⽹图结构初始化为邻接矩阵,⽤来存储顶点直接最短路径权值。将数组p以p[i][j] = j的方式初始化,⽤来存储最短路径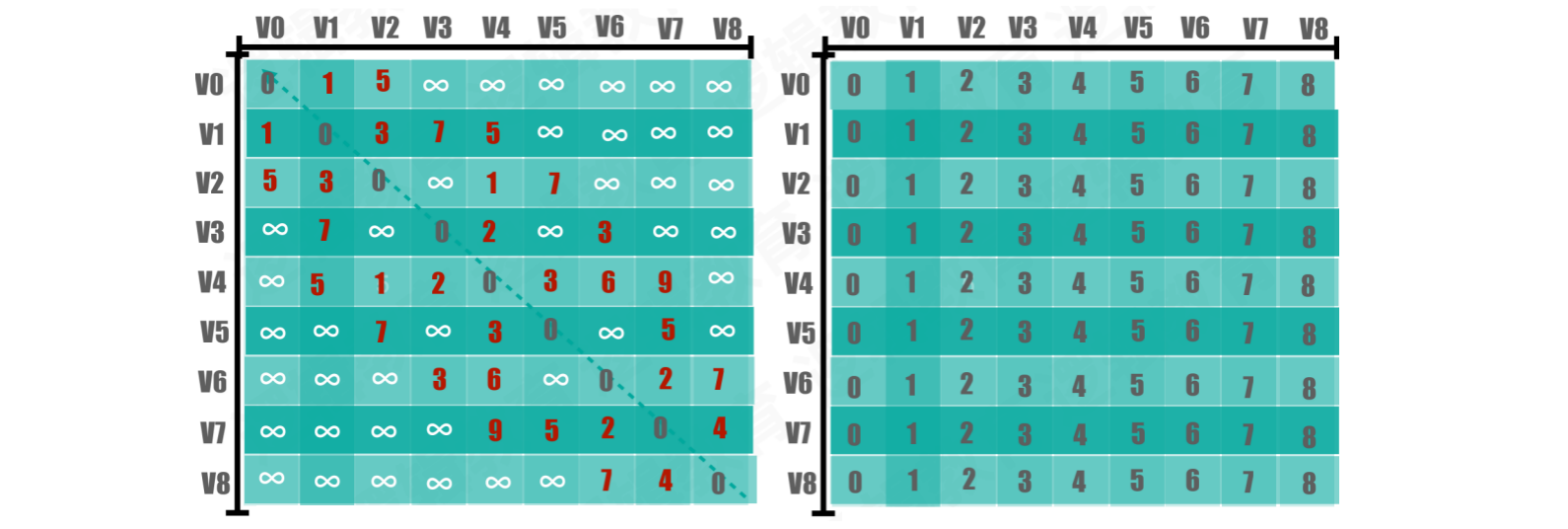
【第一次执行】当k = 0时,V的变化从0 ~ 8,W的变化从0 ~ 8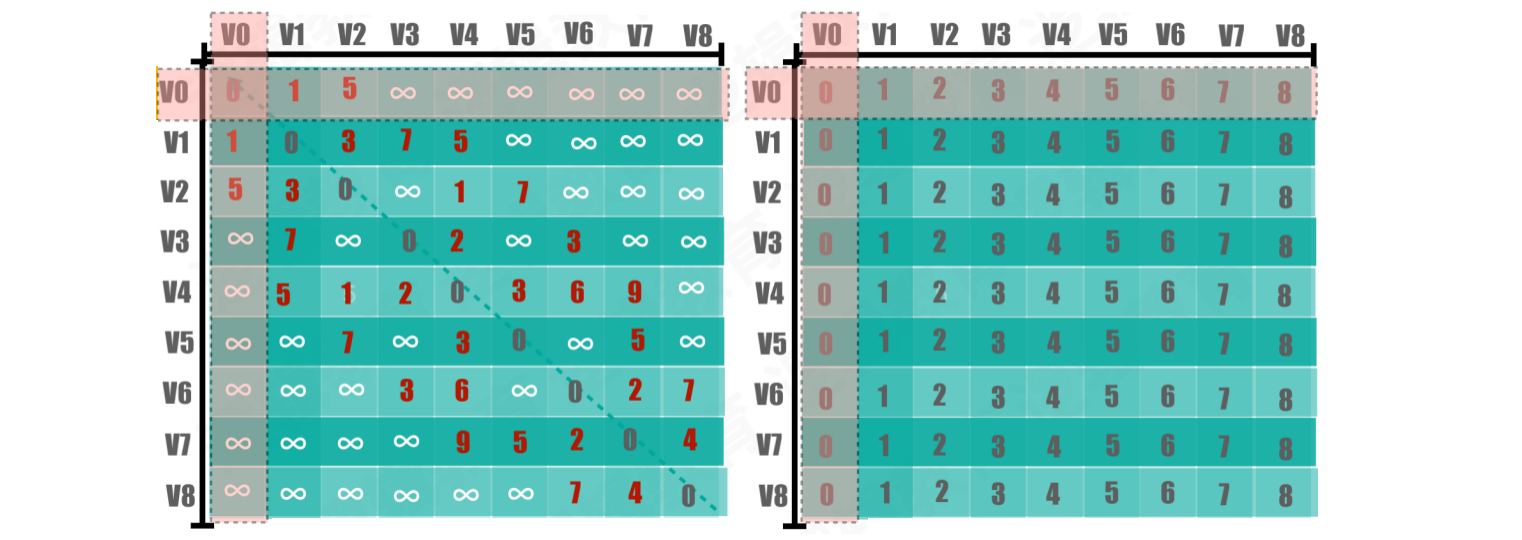
- 当
k = 0时,也就是所有顶点都经过V0中转,计算是否有最短路径的变化。但是k = 0时,并没有发⽣任何变换
【第二次执行】当k = 1时,也就是所有顶点都经过V1中转
数组D执行前后的对比: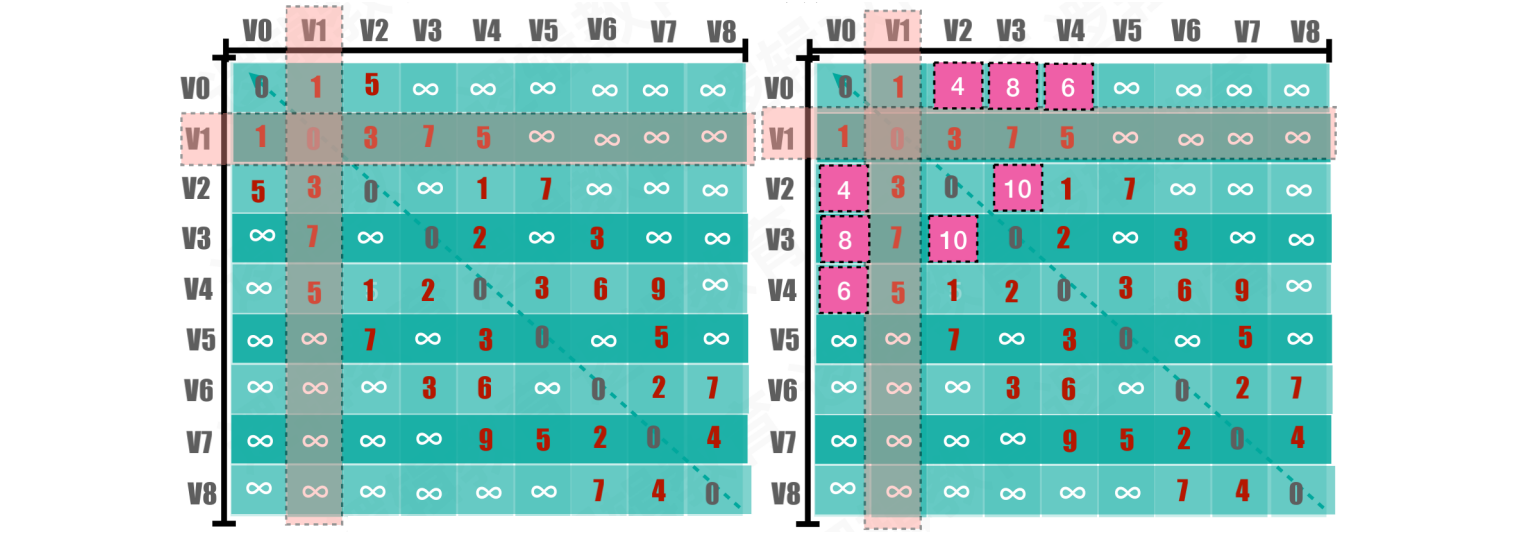
当
k = 1,V = 0,W = [0 ~ 8]时,算法执⾏过程:D[0][0] = 0,D[0][1] + D[1][0] = 1 + 1 = 2,不更新 D[0][1] = 1,D[0][1] + D[1][1] = 1 + 0 = 1,不更新 D[0][2] = 5,D[0][1] + D[1][2] = 1 + 3 = 4,4 < 5,更新D[0][2] = 4 D[0][3] = max,D[0][1] + D[1][3] = 1 + 7 = 8,8 < max,更新D[0][3] = 8 D[0][4] = max,D[0][1] + D[1][4] = 1 + 5 = 6,6 < max,更新D[0][4] = 6 D[0][5] = max,D[0][1] + D[1][5] = 1 + max,不更新 D[0][6] = max,D[0][1] + D[1][6] = 1 + max,不更新 D[0][7] = max,D[0][1] + D[1][7] = 1 + max,不更新 D[0][8] = max,D[0][1] + D[1][8] = 1 + max,不更新当
k = 1,V = 1,W = [0 ~ 8]时,算法执⾏过程:D[1][0] = 1,D[1][1] + D[1][0] = 0 + 1 = 1,不更新 D[1][1] = 0,D[1][1] + D[1][1] = 0 + 0 = 0,不更新 D[1][2] = 3,D[1][1] + D[1][2] = 0 + 3 = 3,不更新 D[1][3] = 7,D[1][1] + D[1][3] = 0 + 7 = 7,不更新 D[1][4] = 5,D[1][1] + D[1][4] = 0 + 5 = 5,不更新 D[1][5] = max,D[1][1] + D[1][5] = 0 + max,不更新 D[1][6] = max,D[1][1] + D[1][6] = 0 + max,不更新 D[1][7] = max,D[1][1] + D[1][7] = 0 + max,不更新 D[1][8] = max,D[1][1] + D[1][8] = 0 + max,不更新当
k = 1,V = 2,W = [0 ~ 8]时,算法执⾏过程:D[2][0] = 5,D[2][1] + D[1][0] = 3 + 1 = 4,4 < 5,更新D[2][0] = 4 D[2][1] = 3,D[2][1] + D[1][1] = 3 + 0 = 3,不更新 D[2][2] = 0,D[2][1] + D[1][2] = 3 + 3 = 6,不更新 D[2][3] = max,D[2][1] + D[1][3] = 3 + 7 = 10,10 < max,更新D[2][3] = 10 D[2][4] = 1,D[2][1] + D[1][4] = 3 + 5 = 8,不更新 D[2][5] = 7,D[2][1] + D[1][5] = 3 + max,不更新 D[2][6] = max,D[2][1] + D[1][6] = 3 + max,不更新 D[2][7] = max,D[2][1] + D[1][7] = 3 + max,不更新 D[2][8] = max,D[2][1] + D[1][8] = 3 + max,不更新当
k = 1,V = 3,W = [0 ~ 8]时,算法执⾏过程:D[3][0] = max,D[3][1] + D[1][0] = 7 + 1 = 8,8 < max,更新D[3][0] = 8 D[3][1] = 7,D[3][1] + D[1][1] = 7 + 0 = 7,不更新 D[3][2] = max,D[3][1] + D[1][2] = 7 + 3 = 10,10 < max,更新D[3][2] = 10 D[3][3] = 0,D[3][1] + D[1][3] = 7 + 7 = 14,不更新 D[3][4] = 2,D[3][1] + D[1][4] = 7 + 5 = 12,不更新 D[3][5] = max,D[3][1] + D[1][5] = 7 + max,不更新 D[3][6] = 3,D[3][1] + D[1][6] = 7 + max,不更新 D[3][7] = max,D[3][1] + D[1][7] = 7 + max,不更新 D[3][8] = max,D[3][1] + D[1][8] = 7 + max,不更新当
k = 1,V = 4,W = [0 ~ 8]时,算法执⾏过程:D[4][0] = max,D[4][1] + D[1][0] = 5 + 1 = 6,6 < max,更新D[4][0] = 6 D[4][1] = 5,D[4][1] + D[1][1] = 5 + 0 = 7,不更新 D[4][2] = 1,D[4][1] + D[1][2] = 5 + 3 = 10,不更新 D[4][3] = 2,D[4][1] + D[1][3] = 5 + 7 = 14,不更新 D[4][4] = 0,D[4][1] + D[1][4] = 5 + 5 = 12,不更新 D[4][5] = 3,D[4][1] + D[1][5] = 5 + max,不更新 D[4][6] = 6,D[4][1] + D[1][6] = 5 + max,不更新 D[4][7] = 9,D[4][1] + D[1][7] = 5 + max,不更新 D[4][8] = max,D[4][1] + D[1][8] = 5 + max,不更新当
k = 1,V = 5,W = [0 ~ 8]时,算法执⾏过程:D[5][0] = max,D[5][1] + D[1][0] = max + 1,不更新 D[5][1] = max,D[5][1] + D[1][1] = max + 0,不更新 D[5][2] = 7,D[5][1] + D[1][2] = max + 3,不更新 D[5][3] = max,D[5][1] + D[1][3] = max + 7,不更新 D[5][4] = 3,D[5][1] + D[1][4] = max + 5,不更新 D[5][5] = 0,D[5][1] + D[1][5] = max + max,不更新 D[5][6] = max,D[5][1] + D[1][6] = max + max,不更新 D[5][7] = 5,D[5][1] + D[1][7] = max + max,不更新 D[5][8] = max,D[5][1] + D[1][8] = max + max,不更新当
k = 1,V = 6,W = [0 ~ 8]时,算法执⾏过程:D[6][0] = max,D[6][1] + D[1][0] = max + 1,不更新 D[6][1] = max,D[6][1] + D[1][1] = max + 0,不更新 D[6][2] = max,D[6][1] + D[1][2] = max + 3,不更新 D[6][3] = 3,D[6][1] + D[1][3] = max + 7,不更新 D[6][4] = 6,D[6][1] + D[1][4] = max + 5,不更新 D[6][5] = max,D[6][1] + D[1][5] = max + max,不更新 D[6][6] = 0,D[6][1] + D[1][6] = max + max,不更新 D[6][7] = 2,D[6][1] + D[1][7] = max + max,不更新 D[6][8] = 7,D[6][1] + D[1][8] = max + max,不更新当
k = 1,V = 7,W = [0 ~ 8]时,算法执⾏过程:D[7][0] = max,D[7][1] + D[1][0] = max + 1,不更新 D[7][1] = max,D[7][1] + D[1][1] = max + 0,不更新 D[7][2] = max,D[7][1] + D[1][2] = max + 3,不更新 D[7][3] = max,D[7][1] + D[1][3] = max + 7,不更新 D[7][4] = 9,D[7][1] + D[1][4] = max + 5,不更新 D[7][5] = 5,D[7][1] + D[1][5] = max + max,不更新 D[7][6] = 2,D[7][1] + D[1][6] = max + max,不更新 D[7][7] = 0,D[7][1] + D[1][7] = max + max,不更新 D[7][8] = 4,D[7][1] + D[1][8] = max + max,不更新当
k = 1,V = 8,W = [0 ~ 8]时,算法执⾏过程:D[8][0] = max,D[8][1] + D[1][0] = max + 1,不更新 D[8][1] = max,D[8][1] + D[1][1] = max + 0,不更新 D[8][2] = max,D[8][1] + D[1][2] = max + 3,不更新 D[8][3] = max,D[8][1] + D[1][3] = max + 7,不更新 D[8][4] = max,D[8][1] + D[1][4] = max + 5,不更新 D[8][5] = max,D[8][1] + D[1][5] = max + max,不更新 D[8][6] = 7,D[8][1] + D[1][6] = max + max,不更新 D[8][7] = 4,D[8][1] + D[1][7] = max + max,不更新 D[8][8] = 0,D[8][1] + D[1][8] = max + max,不更新
【最后一次执行】当k = 8时,也就是所有顶点都经过V8中转,数组D与数组p生成的最终矩阵: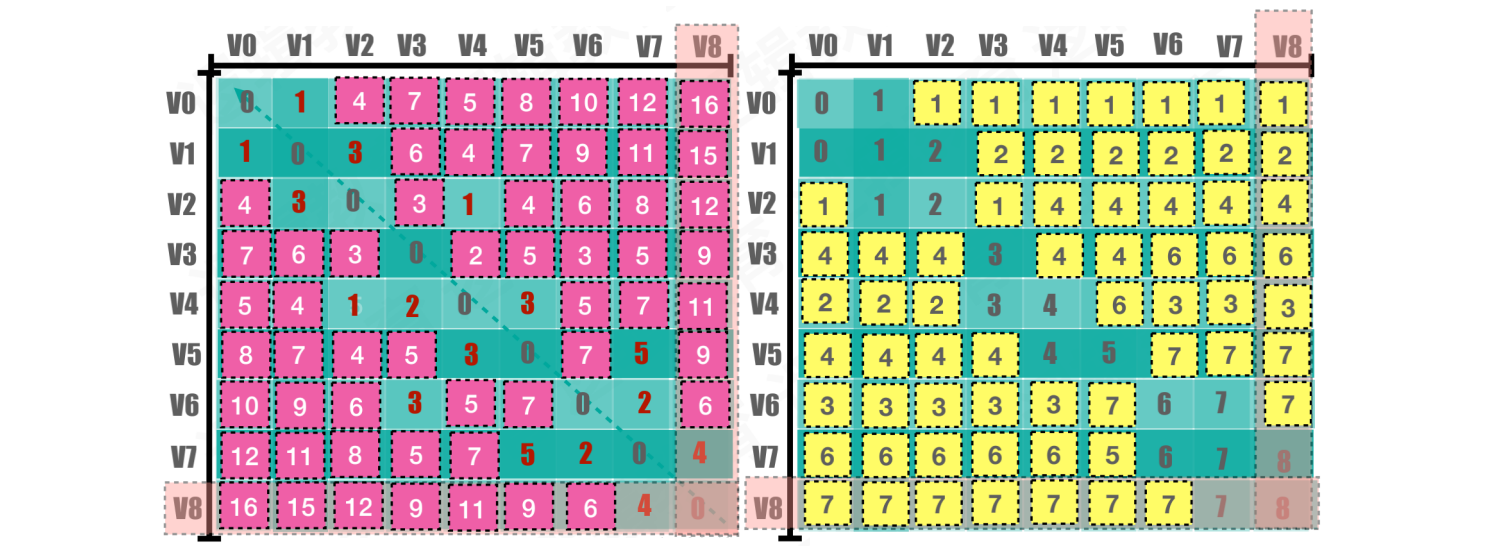
在
数组p中,存储了所有顶点之间的最短路径。以V0 → V8为例:获取p[0][8]位置的值为1,将其作为前驱结点的索引值。获取p[1][8]位置的值为2,按上述逻辑,直到p[0][7]的值为8,此时找到终点,停止遍历在
数组D中,存储了所有顶点之间最短路径所需的权值。以V0 → V8为例:打印D[0][8]即可得到最短路径所需的权值
3.3 代码实现
延用“邻接矩阵存储”的案例代码,修改MGraphLinear类中代码
class MGraphLinear {
var Df : [[Int]]?;
var pf : [[Int]]?;
func shortestPath_floyd(beginIndex : Int, endIndex : Int) -> String {
var str = "";
// 1、初始化数组D与数组p
Df = [[Int]].init(repeating: [Int].init(repeating: 0, count: self.graph.numNodes), count: self.graph.numNodes);
pf = [[Int]].init(repeating: [Int].init(repeating: 0, count: self.graph.numNodes), count: self.graph.numNodes);
// 遍历邻接矩阵
for v in 0 ..< self.graph.numNodes {
for w in 0 ..< self.graph.numNodes {
// 将邻接矩阵中的值填充到Df中
Df![v][w] = self.graph.arc![v][w];
// 将w作为默认值,填充pf
pf![v][w] = w;
}
}
// 2、遍历各顶点之间的最短路径,k为经过的中转顶点
for k in 0 ..< self.graph.numNodes {
// 遍历邻接矩阵
for v in 0 ..< self.graph.numNodes {
for w in 0 ..< self.graph.numNodes {
// 获取起始点到中转点的权值
let weight1 = Df![v][k];
// 获取中转点到结束点的权值
let weight2 = Df![k][w];
// 通过中转点无法连接,跳过
if(weight1 == Int.max || weight2 == Int.max){
continue;
}
// 获取现有路径的权值
let tmp = Df![v][w];
// 计算经过中转的权值
let weight = weight1 + weight2;
// 经过中转的权值 >= 现有路径的权值,跳过
if(weight >= tmp){
continue;
}
// 更新当前位置最短路径的权值
Df![v][w] = weight;
// 更新当前位置对应的前驱结点的索引值
pf![v][w] = pf![v][k];
}
}
}
// 3、打印最短路径的矩阵
str += "最短路径矩阵:\n";
for arr in Df! {
for weight in arr {
if(weight == Int.max){
str += "∞ ";
continue
}
if(weight < 10){
str += "\(weight) ";
continue
}
str += "\(weight) ";
}
str += "\n";
}
// 4、打印前驱结点的矩阵
str += "\n前驱结点矩阵:\n";
for arr in pf! {
for index in arr {
str += "\(index) ";
}
str += "\n";
}
// 5、通过源点和终点,寻找最短路径并打印
var index = pf![beginIndex][endIndex];
str += "\n最短路径:V\(beginIndex)";
while(index != endIndex){
str += " -> V\(index)";
index = pf![index][endIndex];
}
str += " -> V\(endIndex)";
// 6、打印源点到终点最短路径所需的权值总和
str += "\n权值总和:\(Df![beginIndex][endIndex])";
return str;
}
}
按照示例中的网图逻辑,使用代码创建邻接矩阵,并打印Floyd算法的结果:
let nodes = ["V0", "V1", "V2", "V3", "V4", "V5", "V6", "V7", "V8"];
let edges = [[0, 1 ,1], [0, 2, 5],
[1, 2, 3], [1, 3, 7], [1, 4, 5],
[2, 4, 1], [2, 5, 7],
[3, 4, 2], [3, 6, 3],
[4, 5, 3], [4, 6, 6], [4, 7, 9],
[5, 7, 5],
[6, 7, 2], [6, 8, 7],
[7, 8, 4],];
let isUndirected = true;
let isNet = true;
let graphLinear = MGraphLinear();
graphLinear.create(nodes: nodes, edges: edges, isUndirected: isUndirected, isNet: isNet);
print(graphLinear.traverse());
print("\(graphLinear.shortestPath_floyd(beginIndex: 0, endIndex: 8))");
-------------------------
//输出以下内容:
0 1 5 ∞ ∞ ∞ ∞ ∞ ∞
1 0 3 7 5 ∞ ∞ ∞ ∞
5 3 0 ∞ 1 7 ∞ ∞ ∞
∞ 7 ∞ 0 2 ∞ 3 ∞ ∞
∞ 5 1 2 0 3 6 9 ∞
∞ ∞ 7 ∞ 3 0 ∞ 5 ∞
∞ ∞ ∞ 3 6 ∞ 0 2 7
∞ ∞ ∞ ∞ 9 5 2 0 4
∞ ∞ ∞ ∞ ∞ ∞ 7 4 0
最短路径矩阵:
0 1 4 7 5 8 10 12 16
1 0 3 6 4 7 9 11 15
4 3 0 3 1 4 6 8 12
7 6 3 0 2 5 3 5 9
5 4 1 2 0 3 5 7 11
8 7 4 5 3 0 7 5 9
10 9 6 3 5 7 0 2 6
12 11 8 5 7 5 2 0 4
16 15 12 9 11 9 6 4 0
前驱结点矩阵:
0 1 1 1 1 1 1 1 1
0 1 2 2 2 2 2 2 2
1 1 2 4 4 4 4 4 4
4 4 4 3 4 4 6 6 6
2 2 2 3 4 5 3 3 3
4 4 4 4 4 5 7 7 7
3 3 3 3 3 7 6 7 7
6 6 6 6 6 5 6 7 8
7 7 7 7 7 7 7 7 8
最短路径:V0 -> V1 -> V2 -> V4 -> V3 -> V6 -> V7 -> V8
权值总和:16
总结
最短路径问题:
最短路径就是求解,从源点到终点之间,所经过权值最小的路线
较为常用的求解算法有两种:
迪克斯特拉(
Dijkstra)算法弗洛伊德(
Floyd)算法
迪克斯特拉(Dijkstra)算法:
特点:从源点开始,采用贪心算法的策略,每次遍历到始点距离最近且未访问过的顶点的邻接结点,直到扩展到终点为止
思路:
final数组:表示V0到某个顶点Vw是否已经求得了最短路径的标记。如果V0到Vw已经有结果,则final[w] = 1D数组:表示V0到某个顶点Vw的路径p数组:当前顶点的前驱顶点的下标
弗洛伊德(Floyd)算法:
特点:一种利用动态规划的思想寻找给定的加权图中多源点之间最短路径的算法,又称之为插点法
思路:
数组D:代表顶点到顶点的最短路径权值的矩阵数组p:代表对应顶点最短路径的前驱矩阵公式:
D[v][w] = min{ D[v][w], D[v][k] + D[k][w] }k表示经过的中转顶点,变化从0 ~ nv表示邻接矩阵的横向索引位置,变化从0 ~ nw表示邻接矩阵的纵向索引位置,变化从0 ~ n使用该公式遍历最短路径,需要三重循环

