1. 概述

排序定义：假设含有n个记录的序列为（r1, r2, ... rn），其相应的关键字分别为{k1, k2, ... kn}，需确定1, 2, ... n的⼀种排序p1, p2, ... pn，使其相应的关键字满⾜kp1 <= kp2 <= ... <= kpn⾮递减（或⾮递增）关系，即：得到的序列成为⼀个按关键字有序的序列(rp1, rp2, ... rpn)，这样得出操作称为排序

排序的分类：

  • 内排序：是在排序整个过程中，待排序的所有记录全部被放置在内存中

  • 外排序：由于排序的记录个数太多，不能同时放置在内存，整个排序过程需要在内外存之间多次交换数据才能进⾏

排序的结构设计与交换函数实现：

  1. class Sort<Element : Comparable> {
  3.     // 排序数组，索引0位置存储哨兵对象
  4.     fileprivate var _arr : [Element?];
  6.     // 初始化
  7.     init(arr : [Element?]) {
  8.         _arr = arr;
  9.     }
  11.     // 交换函数
  12.     fileprivate func swap(i : Int, j : Int) {
  14.         let tmp = _arr[i];
  15.         _arr[i] = _arr[j];
  16.         _arr[j] = tmp;
  17.     }
  19.     // 打印元素
  20.     func traverse() {
  22.         var str = "";
  24.         for i in 1..<_arr.count {
  25.             str += "\(_arr[i]!), ";
  26.         }
  28.         print("\(str)");
  29.     }
  30. }

2. 冒泡排序

冒泡排序（Bubble Sort）：⼀种交换排序，它的基本思想就是：两两⽐较相邻的记录的关键字，如果反序则交换，直到没有反序的记录为⽌

2.1 初级版本

当i = 1时，9与1交换，之后1与其他关键字⽐较均是最⼩，因此1即最⼩值放置在⾸位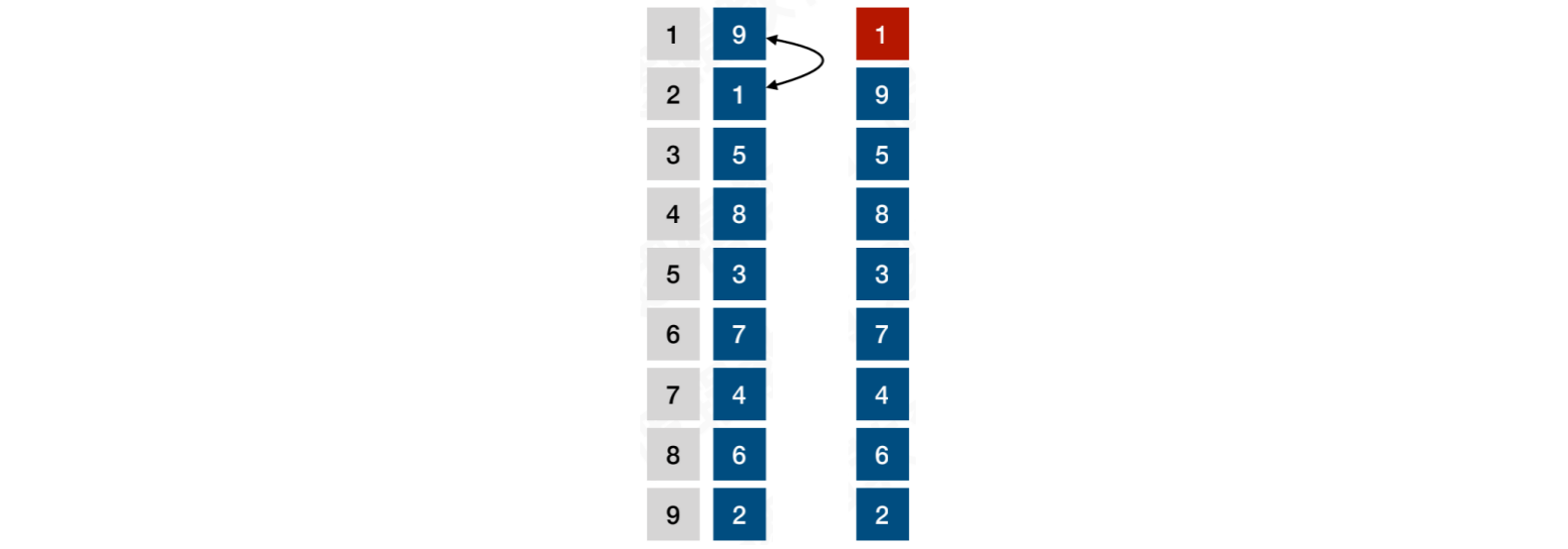
image.png

当i = 2时，9与5交换，5与3交换，3与2交换，最终将2放置第⼆位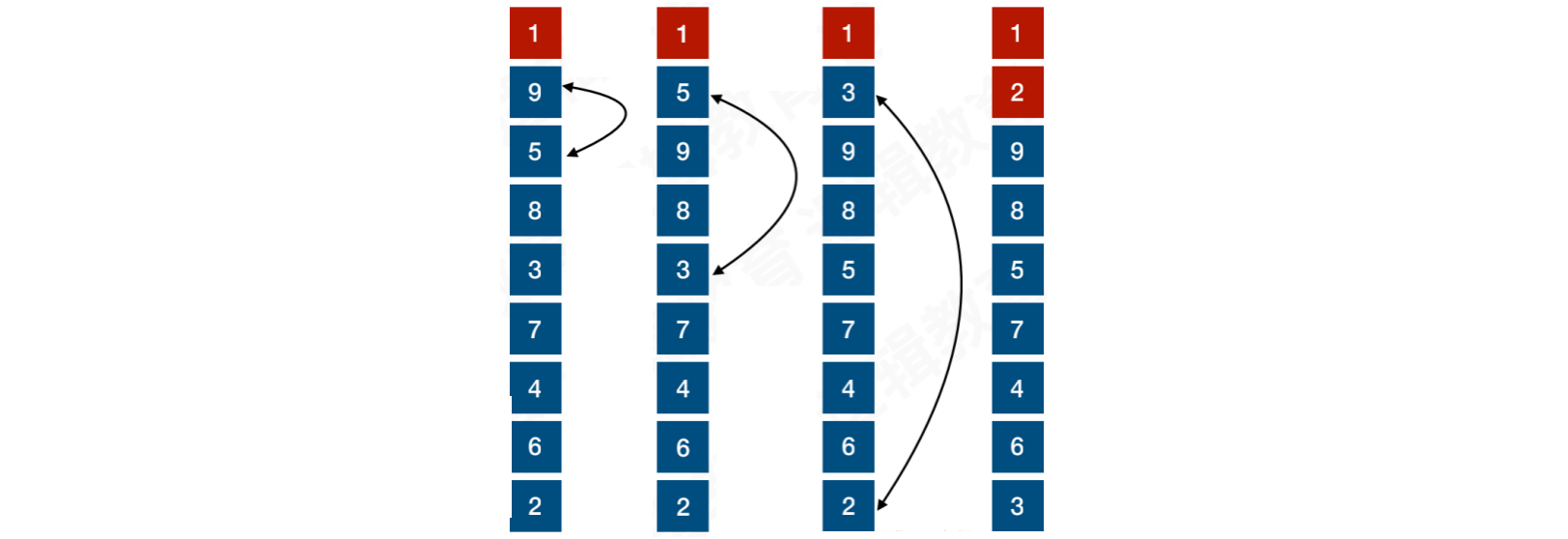
image.png

代码实现：

class Sort<Element : Comparable> {

    // 冒泡排序 - 初级版本
    func bubbleSort_swap(){

        for i in 1..<_arr.count {
            for j in i + 1..<_arr.count {
                if(_arr[i]! > _arr[j]!){
                    swap(i: i, j: j);
                }
            }
        }
    }
}

这种方式，并不符合相邻记录两两⽐较的特性。所以严格来说，只是一个交换排序，而非冒泡排序

时间复杂度：O(n ^ 2)

算法的缺陷：当索引i的元素遍历时，它只是在列表中找到最符合的元素，交换到索引i的位置，对其他元素的排序没有任何帮助

2.2 完成形态

真正的冒泡排序，它在每一次比较中，都会将较小的数据上浮，较大的数据下沉。所以每一次比较，都会对后面其他元素的排序起到帮助

当i = 1时，将最⼩值1冒泡到顶端，顺便将2上浮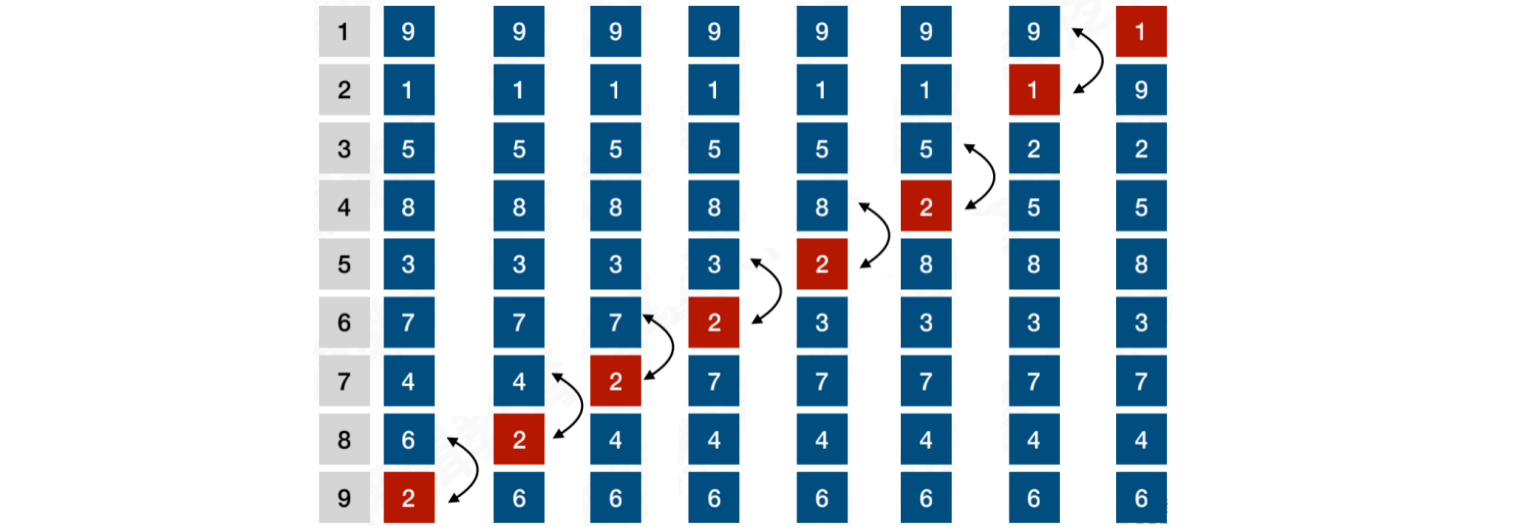
image.png

当i = 2时，将次⼩值2冒泡到顶端，顺便将4和3上浮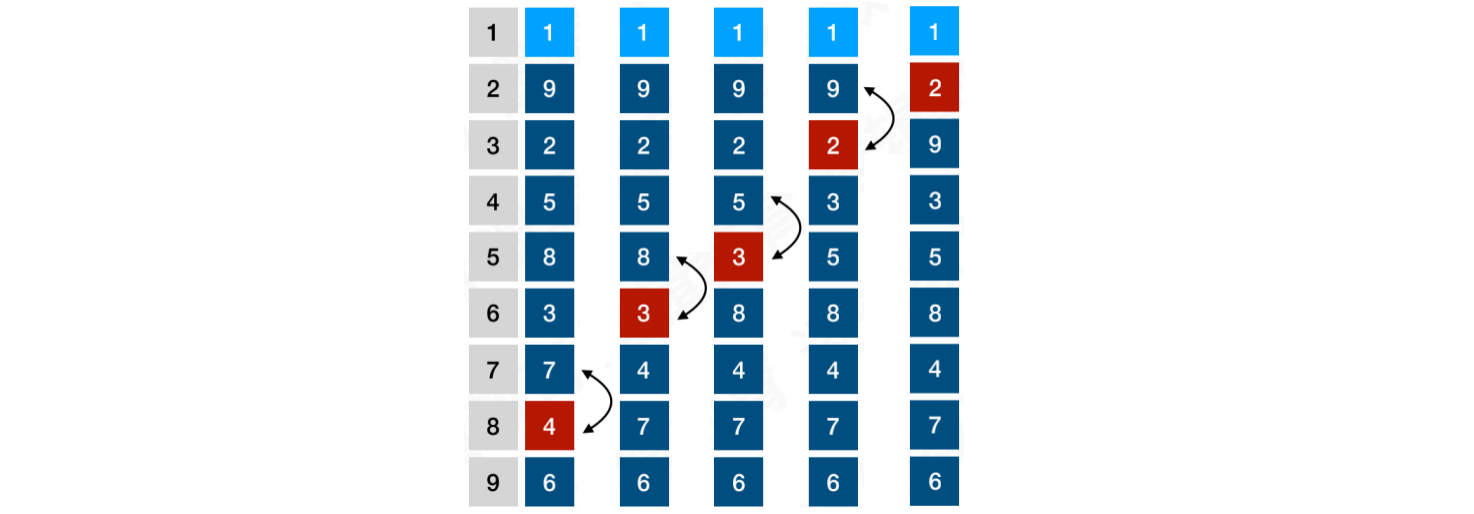
image.png

代码实现：

class Sort<Element : Comparable> {

    // 冒泡排序 - 完成形态
    func bubbleSort(){

        for i in 1..<_arr.count - 1 {
            for j in (i..._arr.count - 2).reversed() {

                let k = j + 1;

                if(_arr[j]! > _arr[k]!){
                    swap(i: j, j: k);
                }
            }
        }
    }
}

时间复杂度：O(n ^ 2)

2.3 排序优化

当i = 1时，将1和2的位置进⾏交换。当i = 2时，如果没有任何数据可交换，则说明此数列已有序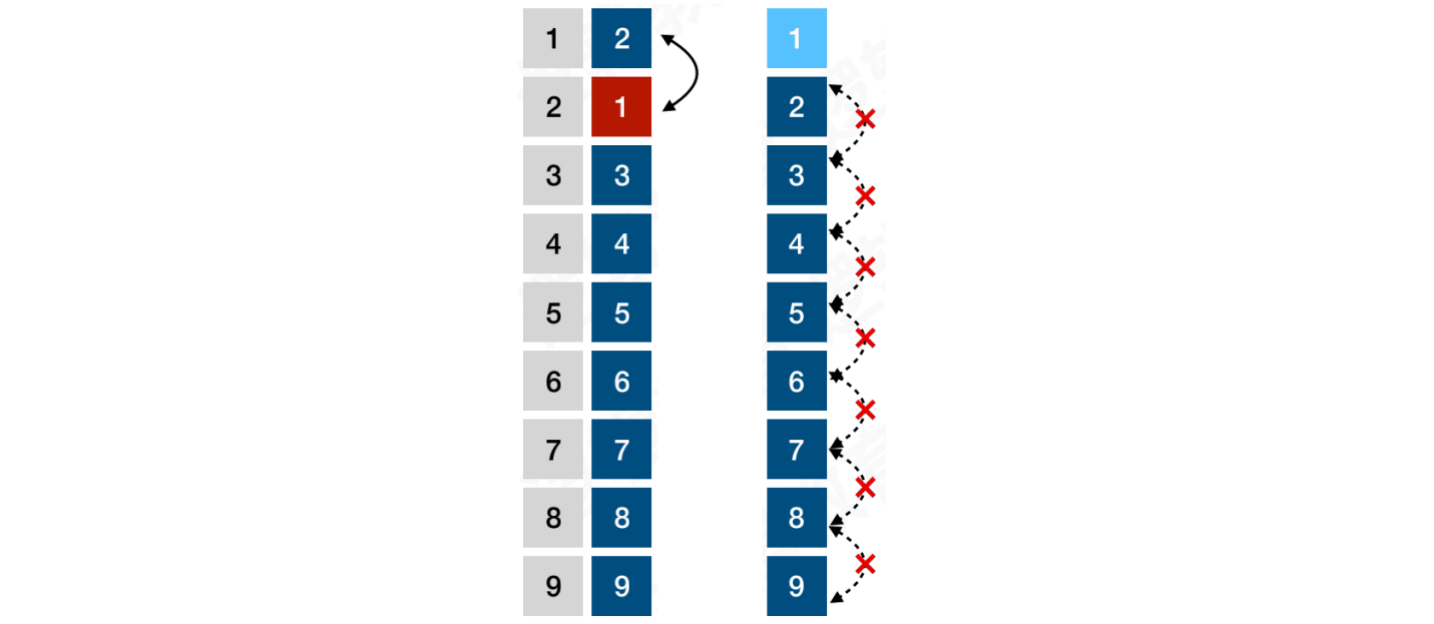
image.png

而之后的所有循环判断，都将是多余的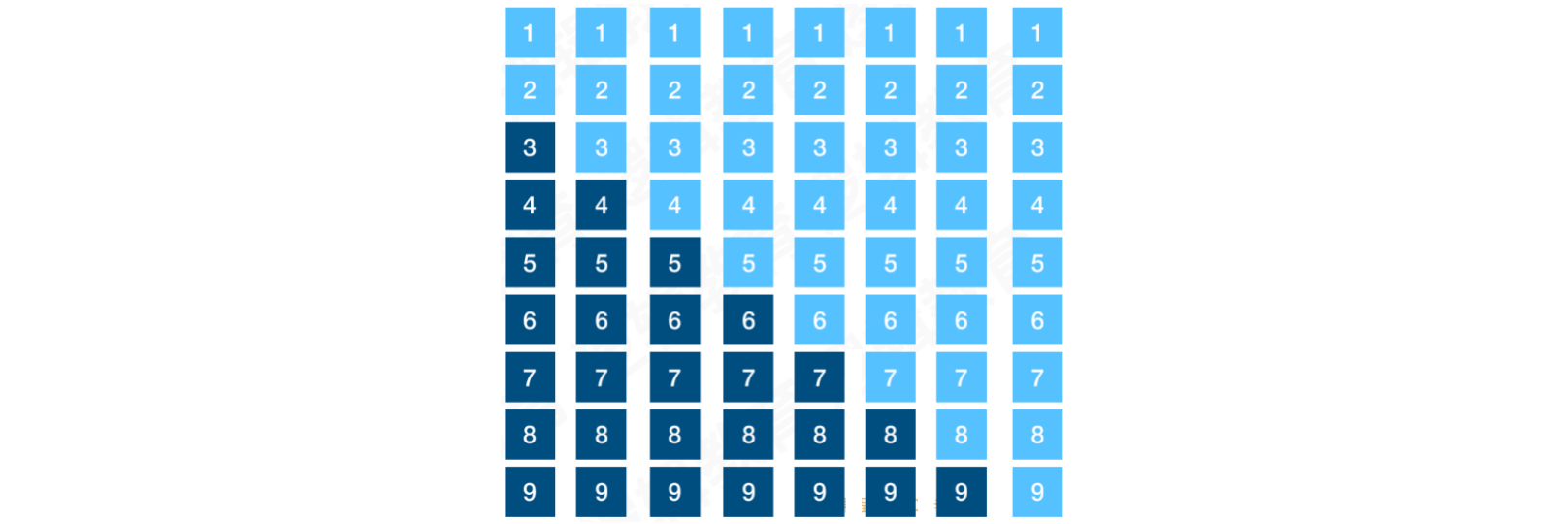
image.png

代码实现：

class Sort<Element : Comparable> {

    // 冒泡排序 - 排序优化
    func bubbleSort_optimize(){

        for i in 1..<_arr.count - 1 {

            var isNeedSort = false;

            for j in (i..._arr.count - 2).reversed() {

                let k = j + 1;

                if(_arr[j]! > _arr[k]!){
                    swap(i: j, j: k);
                    isNeedSort = true;
                }
            }

            if(!isNeedSort){
                break;
            }
        }
    }
}

定义一个标记，外层循环默认为false不需要排序。内层循环中，触发元素交换，则表示此数列无序，将标记改为true需要排序。当一轮内层循环结束时，如果标记为false，表示没有元素需要交换，此数列已有序，退出循环即可

3. 简单选择排序

简单选择排序（Simple Selecton Sort）：就是通过n - i次关键词⽐较，从n - i + 1个记录中找出关键字最⼩的记录，并和第i个记录进⾏交换。i的范围：1 <= i <= n

当i = 1时，位置2的元素1为最小，此时min = 2
image.png

当i = 2时，位置9的元素2为最小，此时min = 9
image.png

当i = 3时，位置5的元素3为最小，此时min = 5
image.png

代码实现：

class Sort<Element : Comparable> {

    // 简单选择排序
    func simpleSelectonSort(){

        for i in 1..<_arr.count - 1 {
            var min = i;

            for j in i + 1..<_arr.count {
                if(_arr[min]! > _arr[j]!){
                    min = j;
                }
            }

            if(min != i){
                swap(i: i, j: min);
            }
        }
    }
}

时间复杂度：O(n ^ 2)

4. 直接插⼊排序

直接插⼊排序（Stight Inserton Sort）的基本操作是将⼀个记录插⼊到已经排好序的有序表中，从⽽得到⼀个新的记录数+1的有序表

循环将i从第2个元素到最后⼀个元素作为待排序元素
image.png

  • 判断当前待排序元素，是否⼩于待排序前⼀个元素（i - 1），如果⼩于则参与接下来的插⼊排序

  • 使⽤临时变量temp存储当前待排序元素：temp = arr[i]

  • 循环遍历，找到元素2之前，能够插⼊的位置。判断依据是从i - 1到0的空间⾥，如果arr[j] > temp，则arr[j + 1] = arr[j]

找到j = i - 1，此时位置j的元素5 > temp，需要将元素5移动到j + 1位置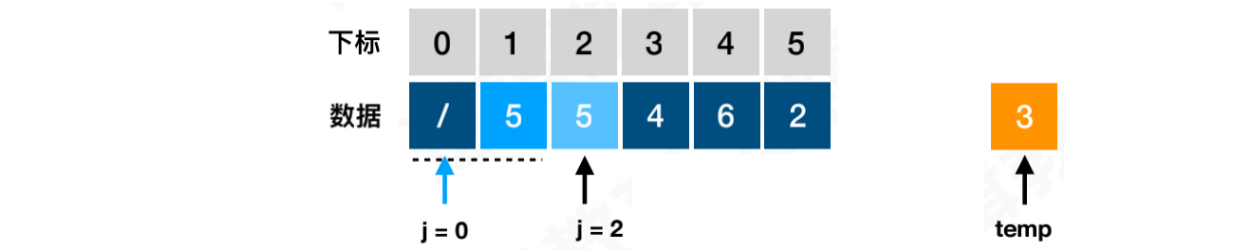
image.png

  • 循环继续，由于位置0元素不⼤于temp，则j层循环结束，⽬前j = 0

  • j层循环中，只要某一个元素不⼤于temp，即可结束循环。因为该元素之前的元素，必然也不会⼤于temp

将3覆盖到位置1，由于j退出循环时等于0，所以是arr[j + 1] = temp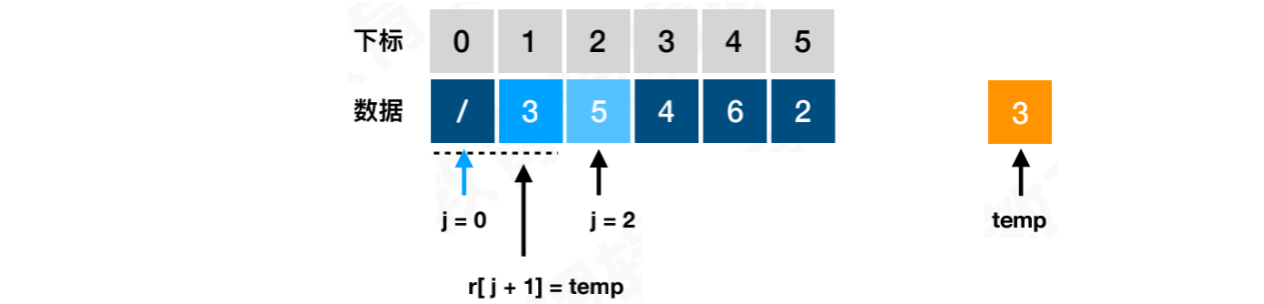
image.png

代码实现：

class Sort<Element : Comparable> {

    // 直接插⼊排序
    func stightInsertonSort(){

        for i in 2..<_arr.count {

            // 如果前一个元素不大于当前元素，跳过本次循环
            if(_arr[i - 1]! <= _arr[i]!){
                continue;
            }

            let temp = _arr[i]!;

            for j in (0..<i).reversed() {

                // 遇到哨兵对象或不大于temp的元素，停止j层循环
                // 将temp赋值到j + 1位置
                if(_arr[j] == nil || _arr[j]! <= temp){
                    _arr[j + 1] = temp;
                    break;
                }

                // 大于temp的元素，全部向后移动一位
                _arr[j + 1] = _arr[j]!;
            }
        }
    }
}

时间复杂度：O(n ^ 2)

5. 希尔排序

希尔排序（Shell Sort）：是把记录按下标的⼀定增量分组，对每组使⽤直接插⼊排序算法排序。随着增量逐渐减少，每组包含的关键词越来越多。当增量减⾄1时，整个数列被分成⼀组，算法终⽌

在计算机学术界，很长一段时间，排序算法的时间复杂度一直维持在O(n ^ 2)。而希尔排序，则是第一个打破O(n ^ 2)的排序算法

希尔排序是在插入排序的基础上进行的优化。而插入排序，在小规模数据且部分有序的情况下，它是最高效的

希尔排序原理，就是在插⼊排序之前，将整个数列调整成基本有序，然后再对全体数列进⾏⼀次直接插⼊排序

5.1 基本有序

基本有序：它会尽可能做到较大的数据在数列尾部，较小的数据在数列头部。当数列是基本有序的情况下，进行插⼊排序是最高效的

它和局部有序的区别很大。局部有序的示例：
image.png

假设将数据分成3组，将其各⾃排序：
image.png

3组数列，局部排序后：
image.png

合并数列，即可得到一个局部有序的数列：
image.png

  • 对局部有序的数列进行插⼊排序，依然是低效的

基本有序和局部有序的数据对比：
image.png

5.2 思路分析

【步骤一】初始化：increment = Length / 2 = 5。这个公式并不是固定的，可以进行调整
image.png

  • 这意味着整个数组被分割成{8, 3}，{9, 5}，{1, 4}，{7, 6}，{2, 0}

在这个分割中，进⾏部分直接插⼊排序。此时3, 5, 6, 0这些⼩元素就会被调整到前⾯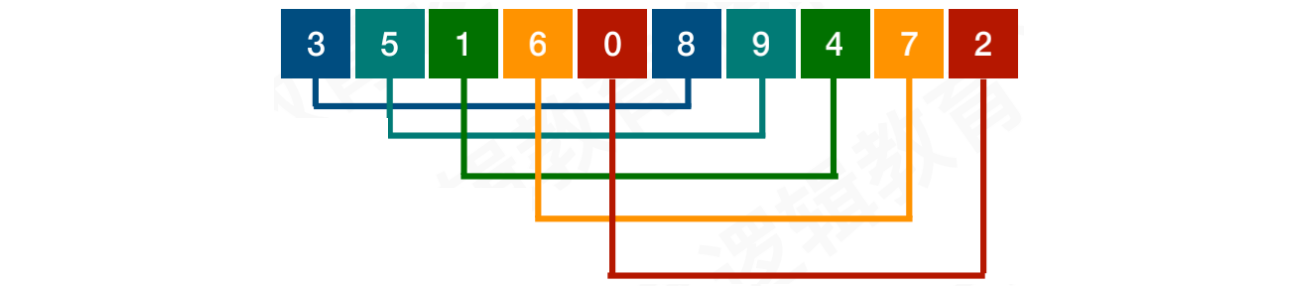
image.png

【步骤二】缩⼩增量：increment = increment / 2 = 5 / 2 = 2
image.png

  • 数组被分为2组：{3, 1, 0, 9, 7}，{5, 6, 8, 4, 2}

对这2个数列进⾏直接插⼊排序
image.png

【步骤三】缩⼩增量：increment = increment / 2 = 2 / 2 = 1
image.png

数组被分为1组。当增量减⾄1时，在这个数组上进⾏直接插⼊排序，算法终⽌
image.png

数组经过3次基本有序的调整后，即可得到最终的有序数列

5.3 算法实现

示例：
image.png

将increment初始化为数组长度，缩⼩增量increment = increment / 3 + 1 = 10 / 3 + 1 = 4。i层循环从increment + 1到length - 1，也就是从5到9。从元素5到元素9都是待插⼊排序元素
image.png

这⾥与插⼊排序的区别是，插⼊排序增减量都是1，也就是与相邻的元素进⾏⽐较。但是在希尔排序⾥，是⼀组的元素才进⾏插⼊排序。即：3与9、2⼀组，1与7⼀组，5与4⼀组，8与6⼀组。同⾊系的数据之间才能进⾏插⼊排序
image.png

模拟i = 5循环，j层循环从i - increment位置开始，位置j的元素9大于待插入元素，则交换
image.png

  • 如果位置j的元素不大于待插入元素，停止j层循环，将待插入元素赋值到j + increment位置

使用哨兵对象存储待插入的元素3，将元素9向后移动至j + increment的位置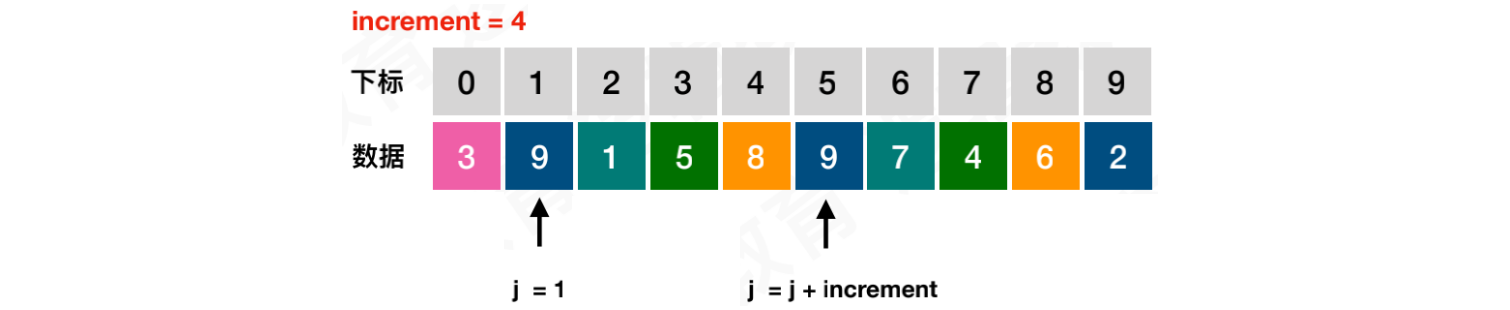
image.png

更新j的索引值，j -= increment，如果j值不大于0，停止j层循环，将哨兵对象中的待插入元素，赋值到j + increment的位置
image.png

  • 上述流程循环往复，当增量减⾄1时，算法终⽌

代码实现：

class Sort<Element : Comparable> {

    //希尔排序
    func shellSort(){

        // 初始化
        var increment = _arr.count;

        // 当增量减⾄1时，算法终⽌
        repeat {

            // 增量序列
            increment = increment / 3 + 1;

            // i的移动范围，从increment + 1到数组最后一个元素
            for i in increment + 1..<_arr.count {

                // 位置i元素为待插⼊元素，i - increment位置的元素为前一个元素
                // 如果前一个元素不大于当前元素，跳过本次循环
                if(_arr[i - increment]! <= _arr[i]!){
                    continue;
                }

                // 将待插⼊元素赋值给临时变量，这里使用哨兵对象
                _arr[0] = _arr[i]!;
                // 初始化j的位置，默认从i - increment位置，即前一个元素开始
                var j = i - increment;

                // 当j减到不大于0时，结束j层循环
                while(j > 0){

                    // 位置j元素不大于待插⼊元素，停止j层循环
                    if(_arr[j]! <= _arr[0]!){
                        break;
                    }

                    // 将位置j元素后移
                    _arr[j + increment] = _arr[j];
                    // 更新j的索引值
                    j -= increment;
                }

                // 由于j层循环的停止条件，结束时j会多减一次increment
                // 所以将待插⼊元素，赋值到j + increment位置
                _arr[j + increment] = _arr[0]!;
            }

        }while(increment > 1)
    }
}

5.4 时间复杂度

算法的时间复杂度与步⻓序列有关：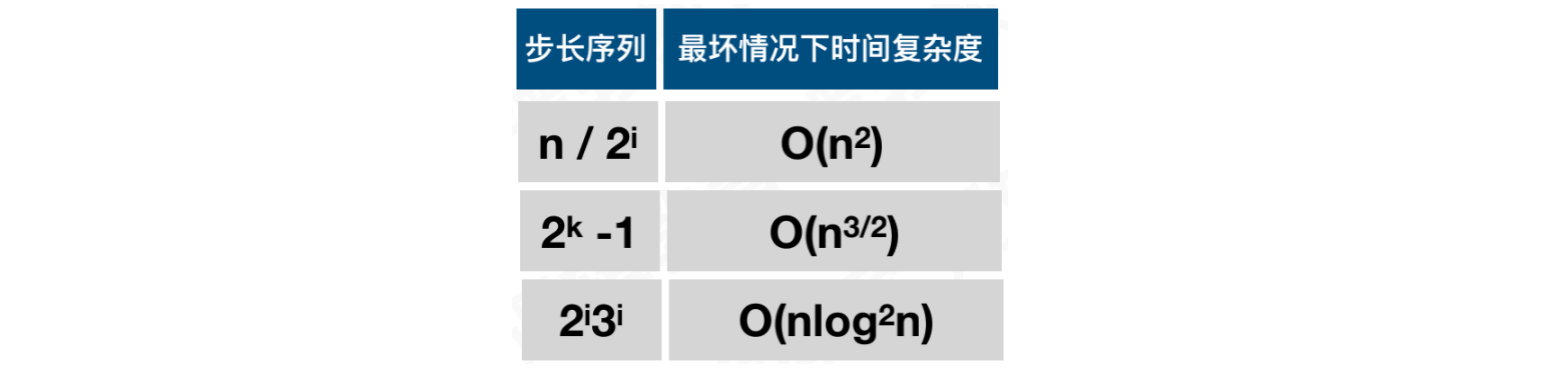
image.png

  • 目前为止，增量序列有一些推荐使用的公式。但如何设计一个最高效的增量序列，仍是未解难题

6. 堆排序

堆排序是简单选择排序的一种进阶，它引用了简单选择排序的思想。在1964年由弗洛伊德（Floyd）与威廉姆斯（J．Williams）共同发明，同时还发明了称之为堆的数据结构

6.1 堆的结构

堆是具有下⾯性质的完全⼆叉树：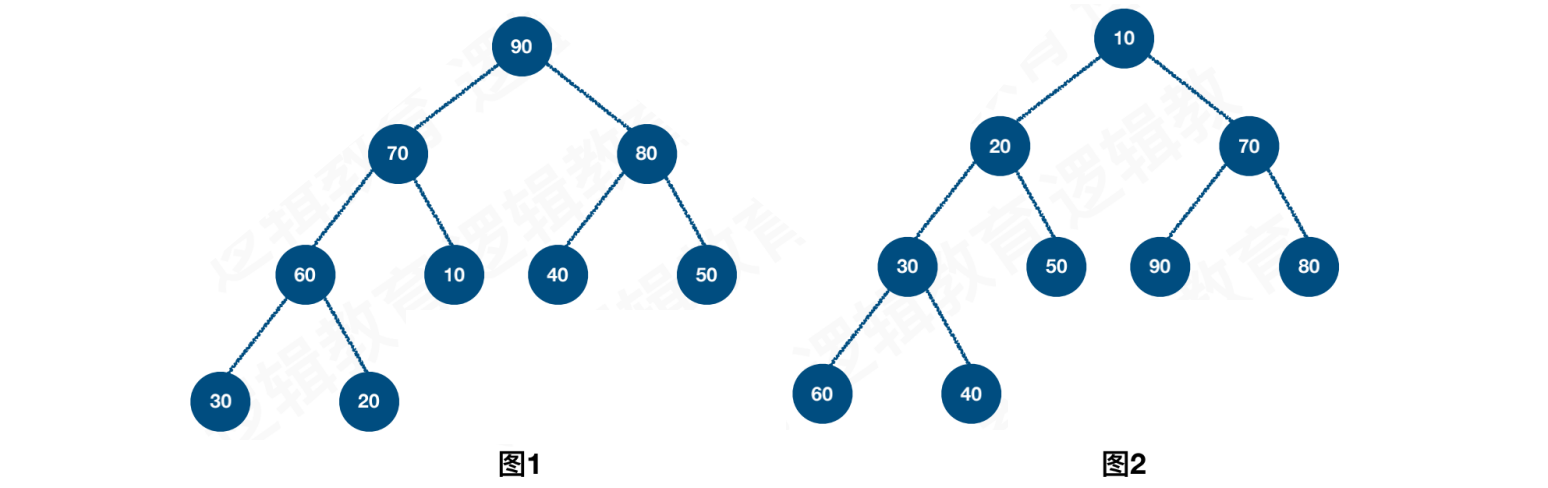
image.png

  • 每个结点的值都⼤于或等于其左右孩⼦结点的值，称为⼤顶堆，如图1

  • 或者，每个结点的值都⼩于等于其左右孩⼦的结点的值，称为⼩顶堆，如图2

如果按照层序遍历的⽅式给结点从1开始编号，则结点之间的满⾜如下关系：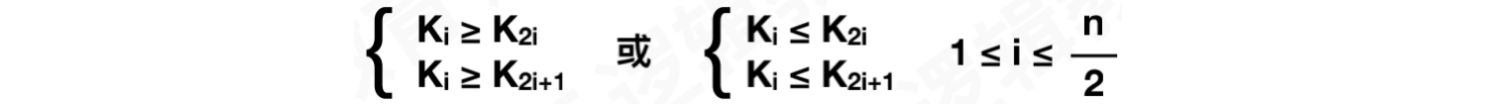
image.png

大顶堆可按照层序进行顺序存储，结点Ki的左右孩子为K2i与K2i + 1。根据大顶堆的特性，结点Ki的值一定大于K2i与K2i + 1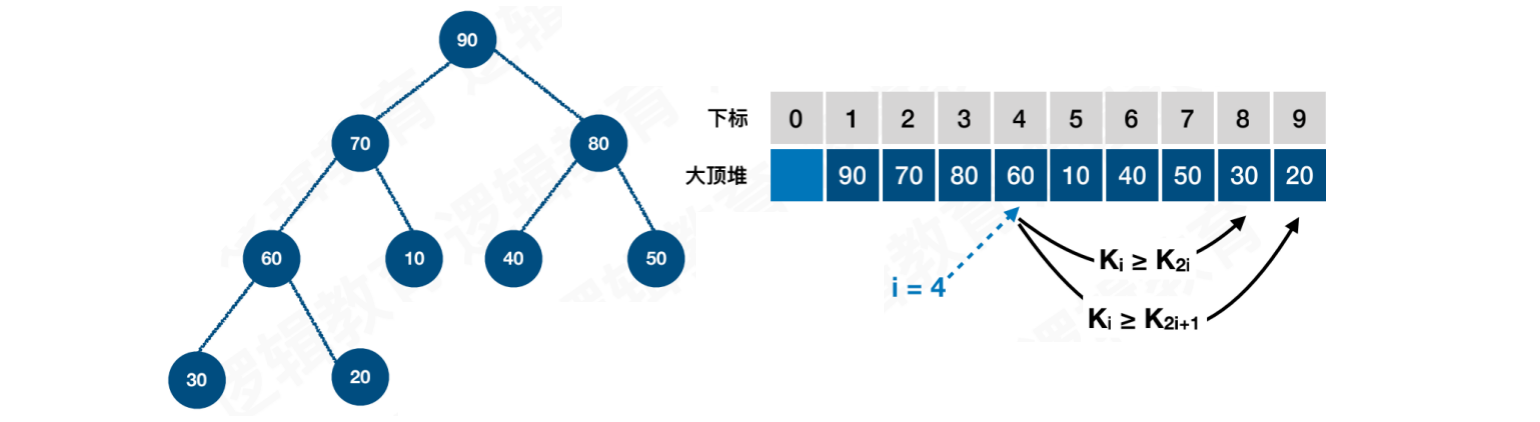
image.png

同理，小顶堆的存储也是如此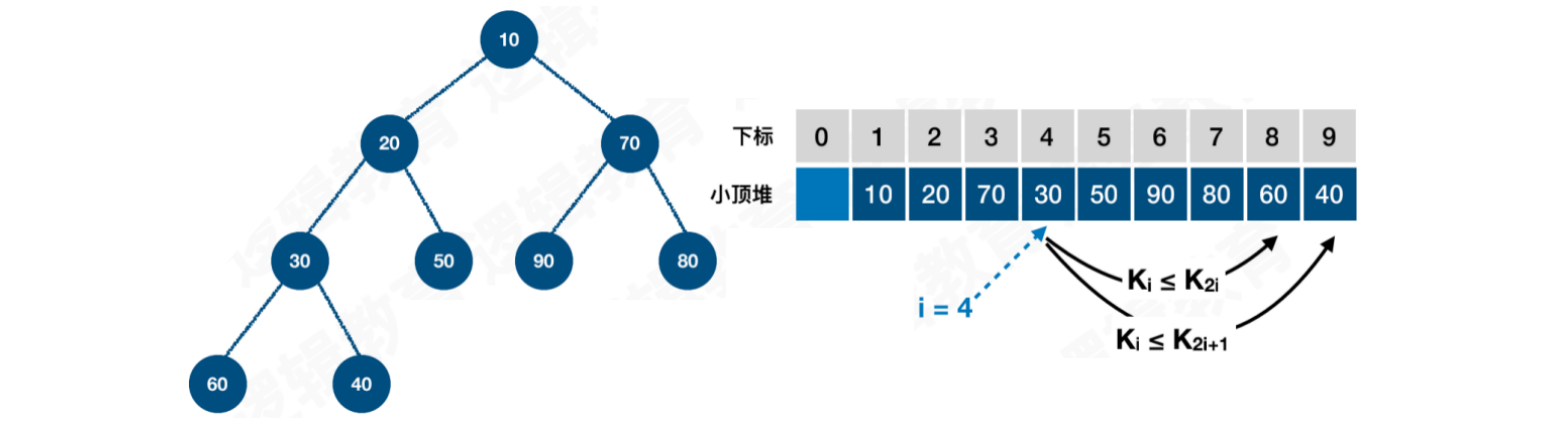
image.png

6.2 思路分析

堆排序（Heap Sort）就是利⽤堆（假设⼤顶堆）进⾏排序的算法，它的基本思想：

  • 将待排序的数列构成⼀个⼤顶堆。此时，整个数列的最⼤值就堆顶的根结点。将它移⾛（其实就是将其与堆数组的末尾元素交换），此时末尾元素就是最⼤值

  • 然后将剩余的n - 1个数列重新构成⼀个堆，这样就会得到n个元素的次⼤值，如此重复执⾏，就能得到⼀个有序数列了

【步骤一】构造初始堆

将给定⽆序数列构造成⼀个⼤顶堆（⼀般升序采⽤⼤顶堆，降序采⽤⼩顶堆）
image.png

从最后⼀个⾮叶⼦结点开始，从左往右，从下往上进⾏调整。而叶子结点则不需要调整。找到位置2的结点6，它的值不能小于它的左右孩⼦。我们要找到[6, 5, 9]三个结点的最⼤值，放置到位置2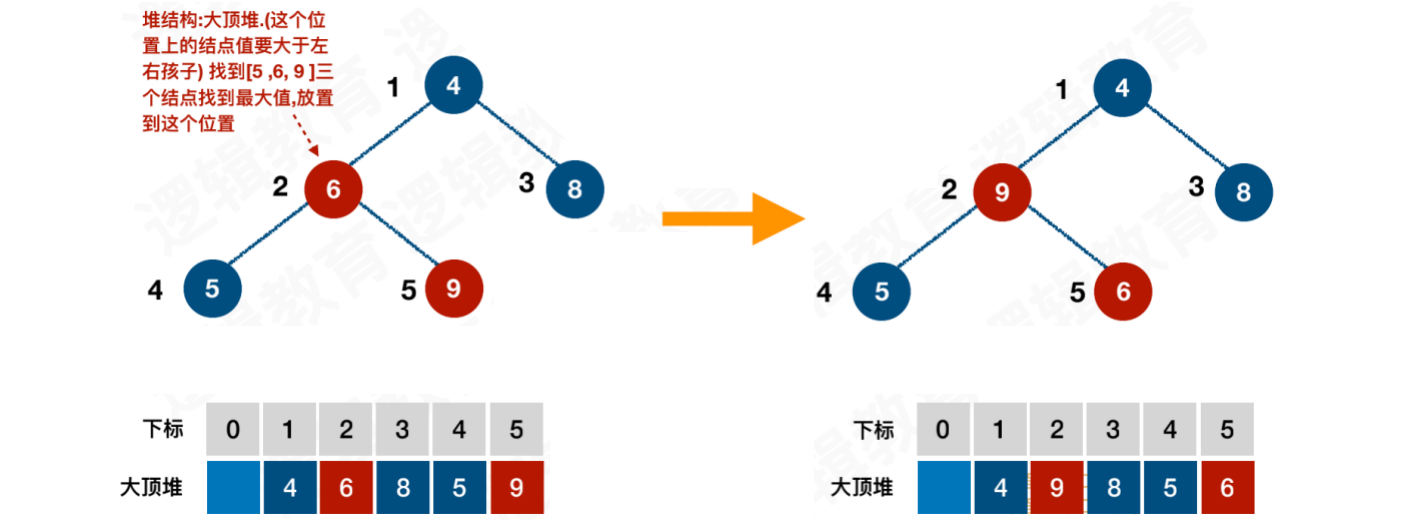
image.png

找到第⼆个⾮叶⼦结点4，从[4, 9, 8]中找到最⼤值，放置到该位置。即：4与9进⾏交换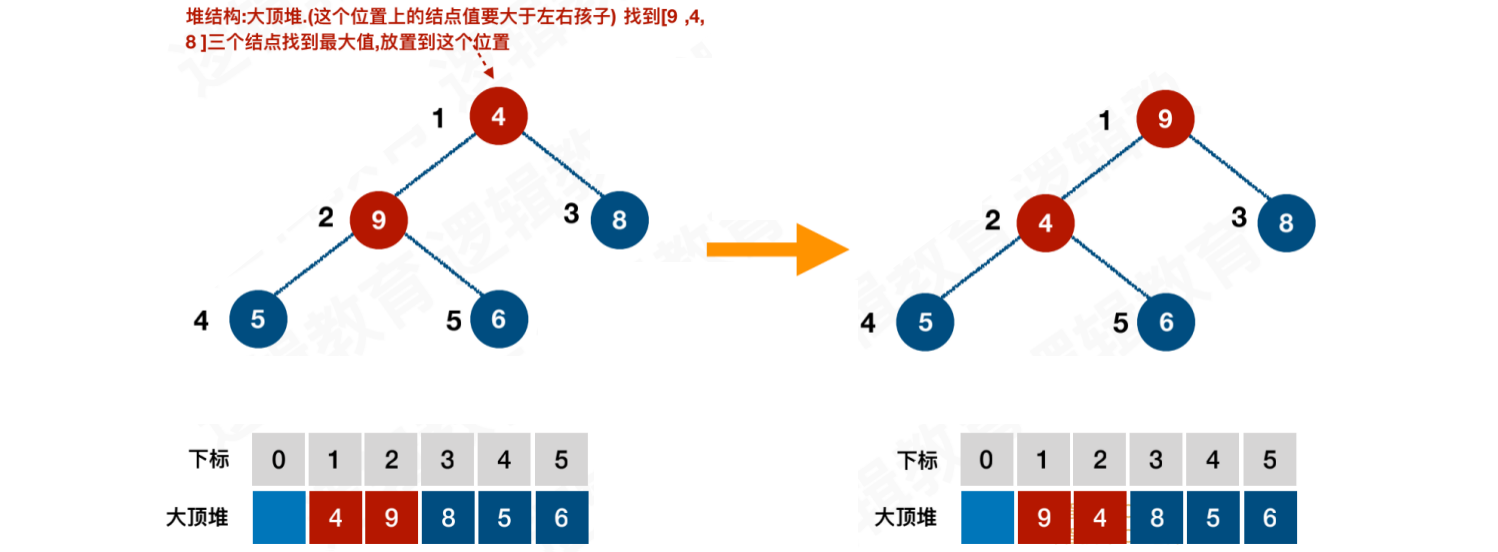
image.png

此时的交换，导致结点[4 ,5 ,6]结构混乱。继续调整，从[4, 5, 6]中找到最⼤的结点6，交换4与 6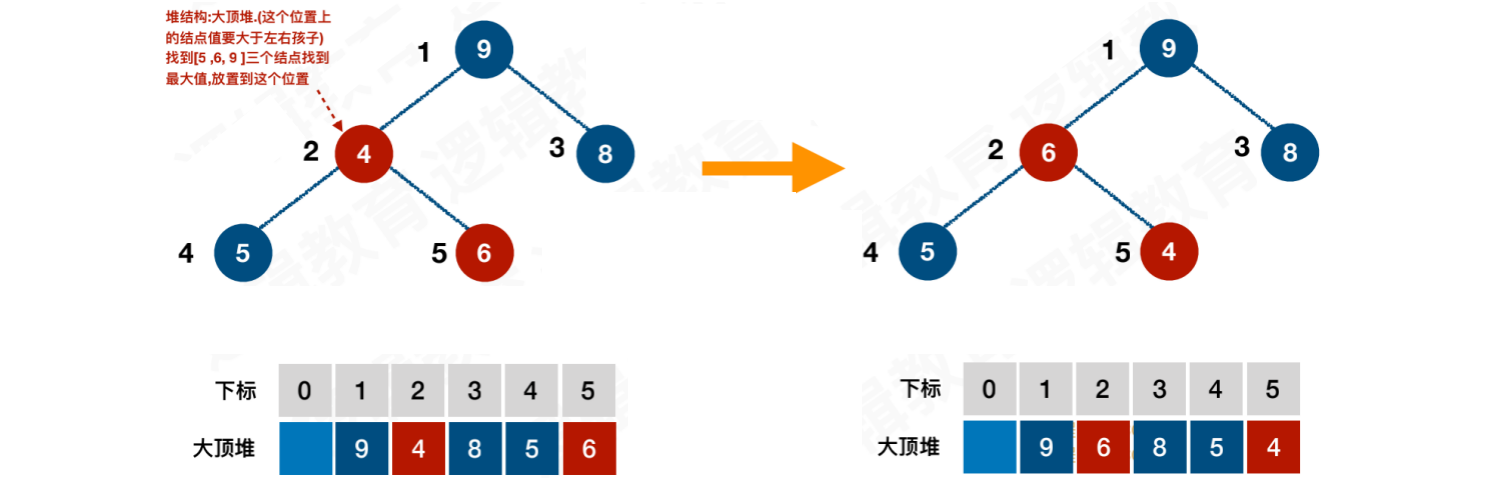
image.png

  • 经过上述3次调整，将之前的⽆序数列调整为⼤顶堆结构

【步骤二】将堆顶元素与末尾元素进⾏交换，使末尾元素最⼤。然后继续调整堆，再将堆顶元素与
末尾元素交换，得到第⼆⼤元素。如此反复进⾏交换、重建、交换

将堆顶元素9和末尾元素4进⾏交换，此时9将不参与后续的堆排序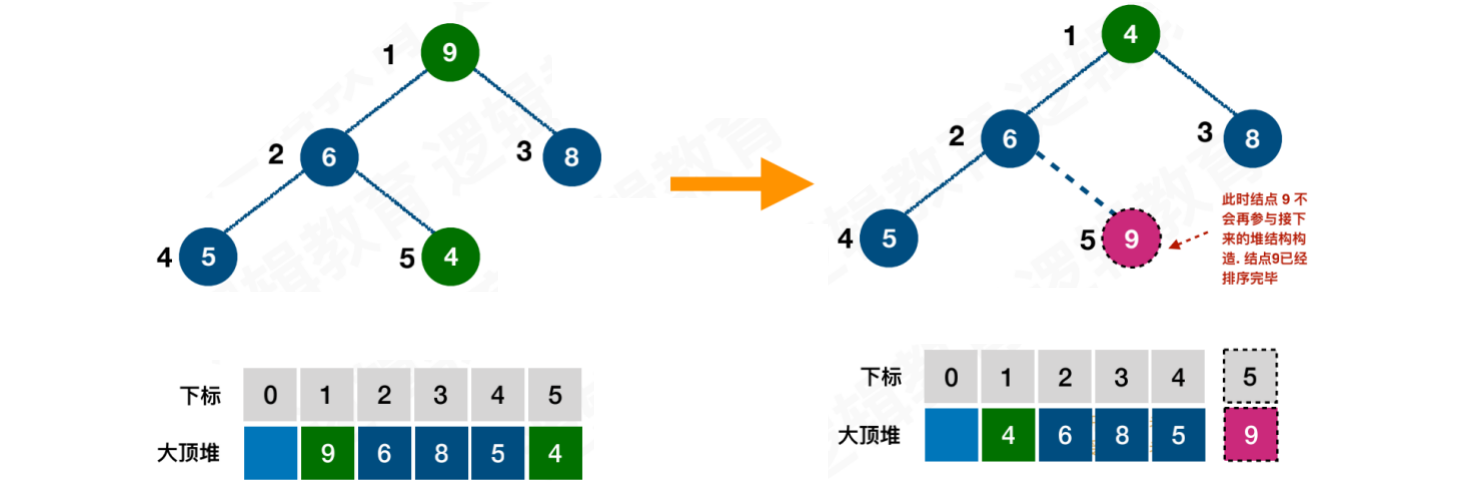
image.png

重新调整结构，使其满⾜⼤顶堆的定义。从[4, 6, 8]中找到最⼤值，即4与8进⾏交换。调整后，⼜得到了⼀个⼤顶堆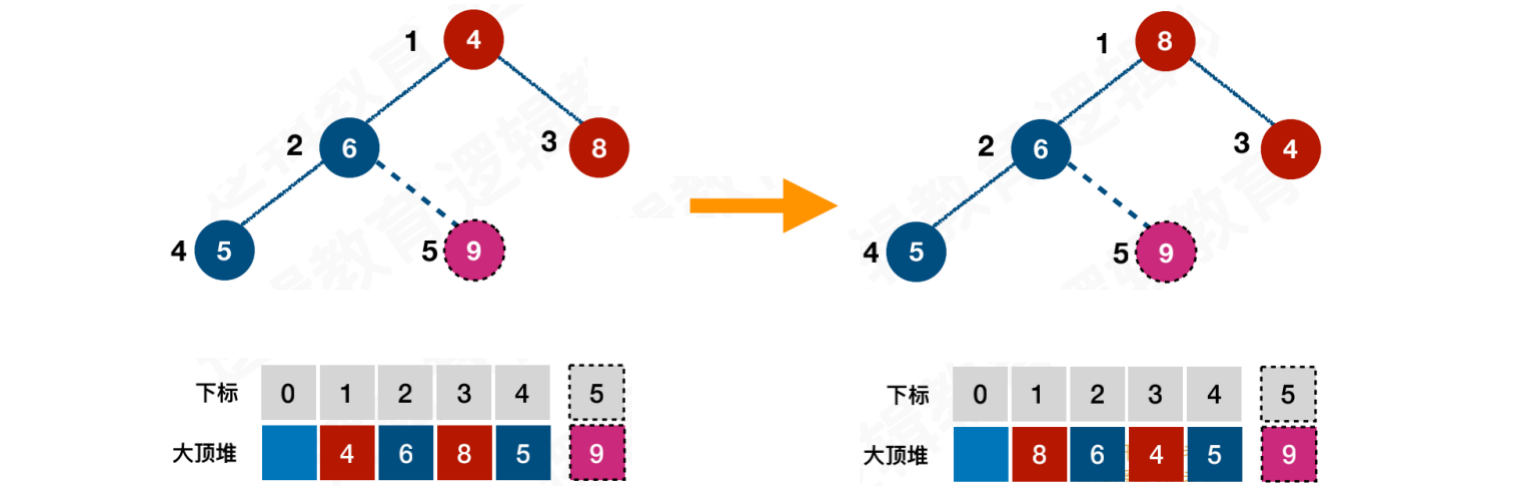
image.png

再将堆顶元素8与末尾元素5进⾏交换，得到第⼆⼤的元素8
image.png

【步骤三】后续的过程，继续进⾏调整，交换，如此反复进⾏，最终使得整个数列有序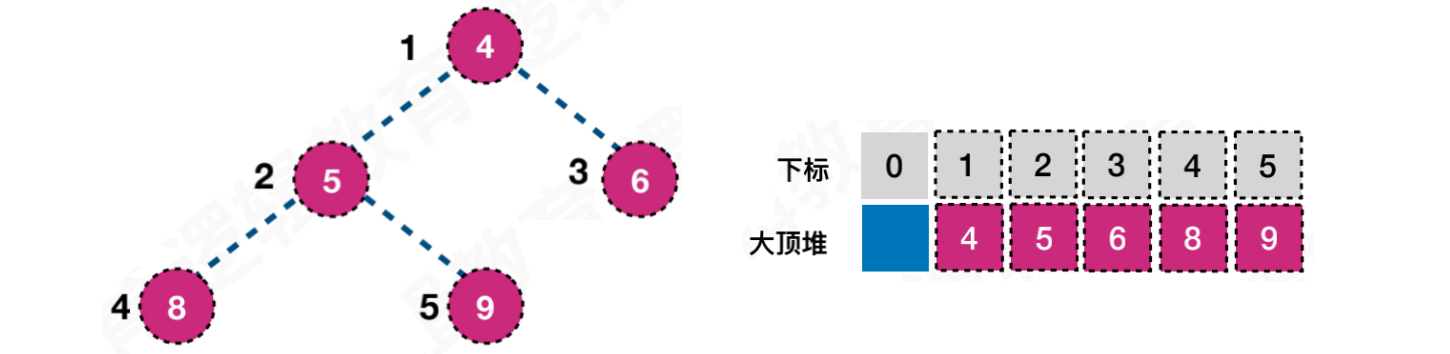
image.png

堆排序的思路总结：

  • 将无序数列构建成⼀个堆，根据升序降序需求选择⼤顶堆或⼩顶堆

  • 将堆顶元素与末尾元素交换，将最⼤元素“沉”到数组末端

  • 重新调整结构，使其满⾜堆定义，然后继续交换堆顶元素与当前末尾元素，反复执⾏调整 + 交换步骤，直到整个数列有序

6.3 算法实现

堆具有完全⼆叉树的性质，如果对一棵有n个结点的完全⼆叉树的结点按层序编号，对任⼀结点i（1 <= i <= n）有：

  • 如果i = 1，则结点i是⼆叉树的根，⽆双亲。如果i > 1，则其双亲是结点i / 2

  • 如果2i > n，则结点i⽆左孩⼦（结点i为叶⼦结点），否则左孩⼦是结点2i

  • 如果2i + 1 > n，则结点i⽆右孩⼦，否则其右孩⼦是结点2i + 1

示例：

【步骤一】i层循环，从i = n / 2开始，到i = 1结束。i按照4 → 3 → 2 → 1的顺序，依次遍历所有非叶子结点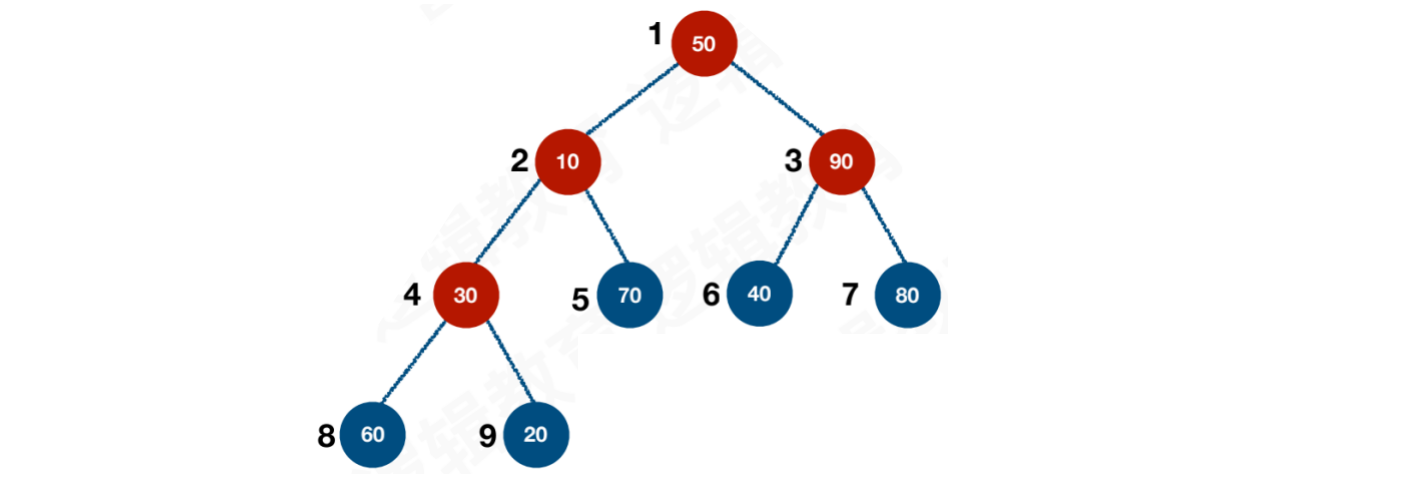
image.png

【步骤二】进入j层循环，默认j = i，j >= n时停止。当i = 4时，需要调整的范围为4 ~ 9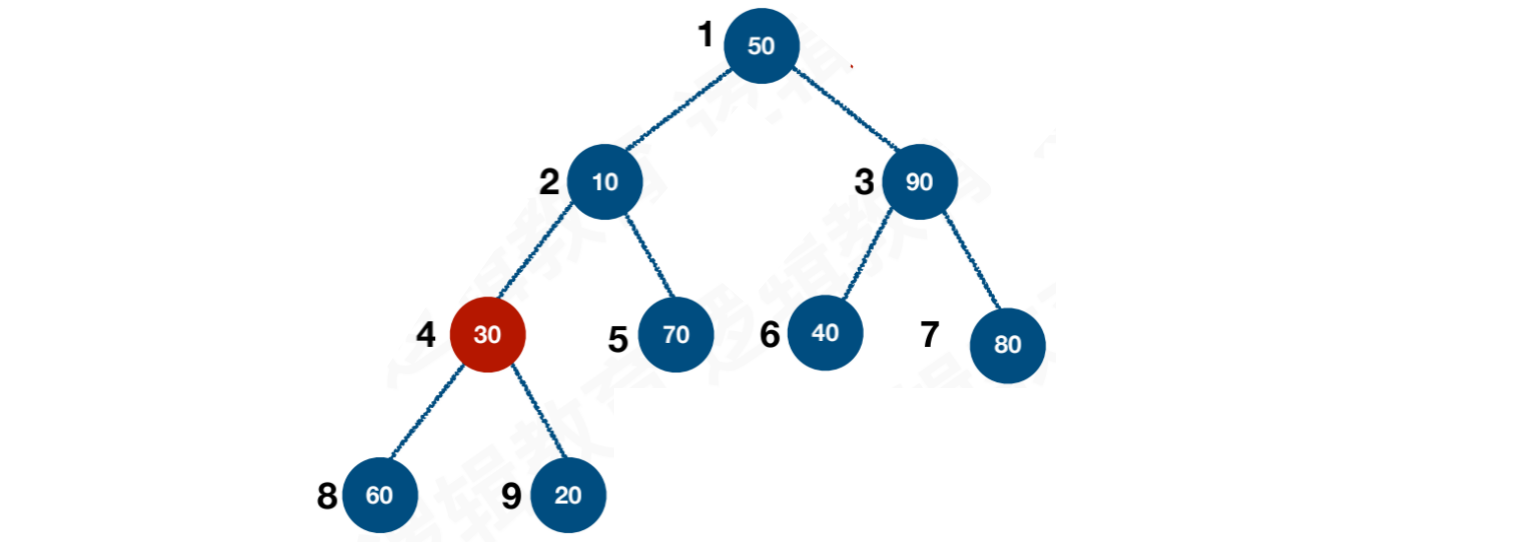
image.png

【步骤三】虽然范围是4 ~ 9，但实际需要调整的，仅为4、8、9即可，也就是当前根结点与它的左、右孩子。可以通过i * 2得到左孩子，i * 2 + 1得到右孩子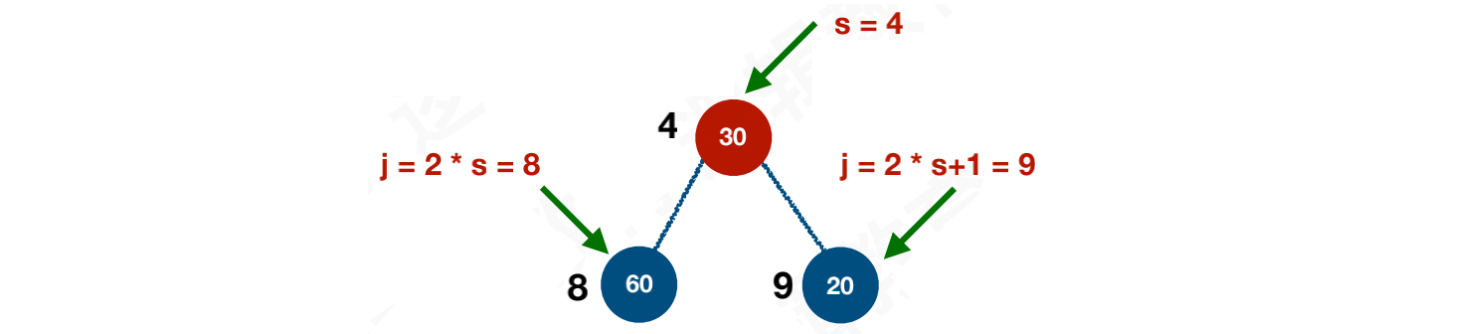
image.png

  • 判断左孩子是否超过n，如果超过，则表示当前结点为叶子结点，不需要调整，结束j层循环

    • 否则，定义临时变量targetIndex，用于存储即将交换的索引值，默认targetIndex = leftIndex，即：左孩子的索引值

  • 判断右孩子是否超过n，如果超过，则表示当前结点下只有左孩子结点，进入后续流程

    • 否则，对比左、右孩子。如果右孩子比左孩子更符合【大/小顶堆】的特性，更新targetIndex = rightIndex，即：右孩子的索引值

  • 对比根结点与即将交换的结点。如果根结点更符合【大/小顶堆】的特性，则不需要调整，结束j层循环

    • 否则，交换j与targetIndex的元素，将j赋值为targetIndex，并准备进入下一轮j层循环

  • 以上过程循环往复，当i层循环结束，表示已经将无序数列调整为【大/小顶堆】

【步骤四】进入堆排序流程，从最后一个结点开始，依次和根结点交换。从c = n - 1开始，到c > 1结束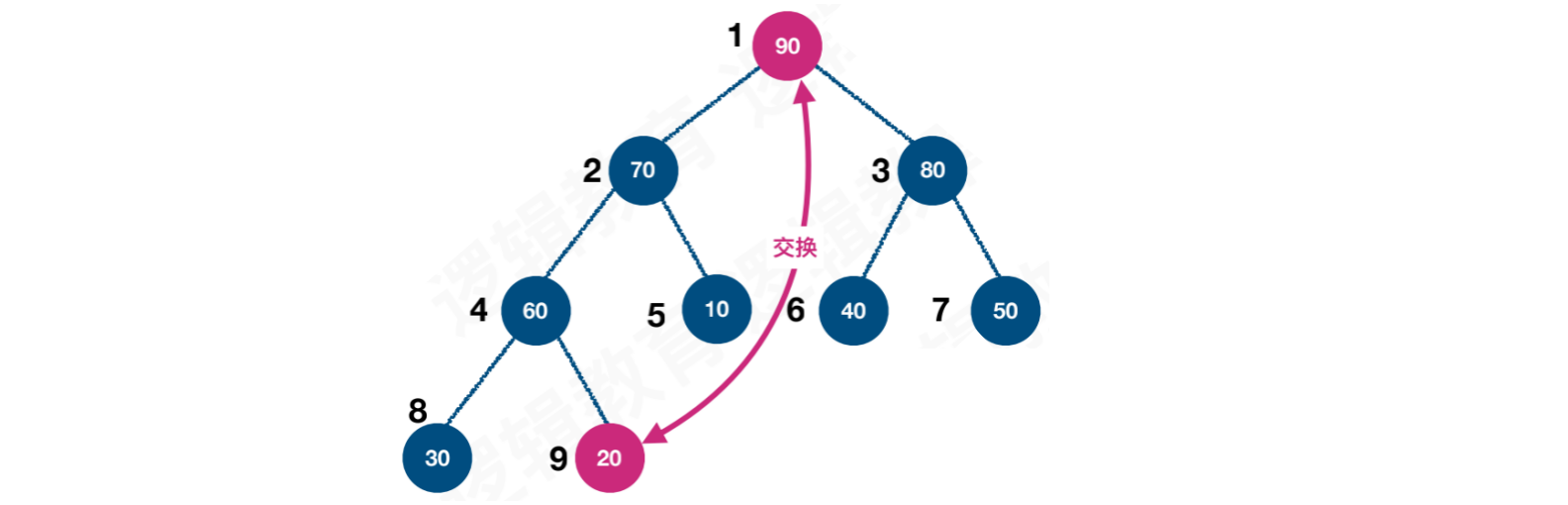
image.png

【步骤五】与根结点交换后，再次调整树结构，使其符合【大/小顶堆】的特性。调整范围为1 ~ c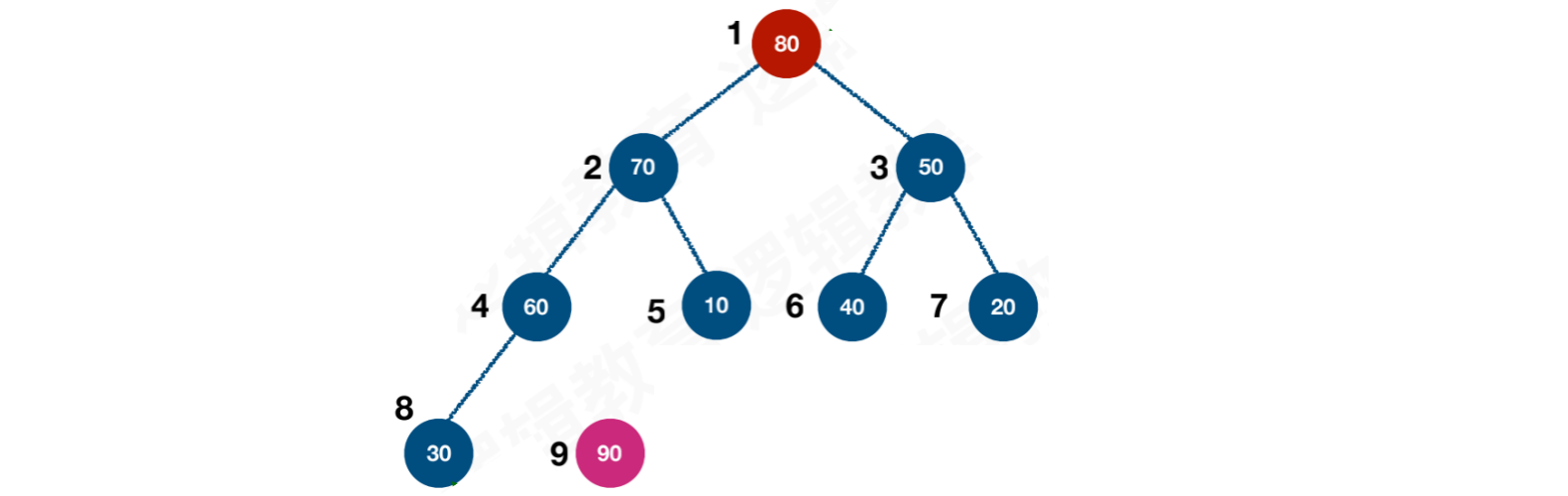
image.png

  • c在每一轮遍历中，都会递减。也就是说，交换后的调整，不包含本轮被交换到数列尾部的结点

  • 以上过程循环往复，当c层循环结束，我们即可得到一个有序数列

代码实现：

// 排序方式
enum SortType : Int {
    // 升序
    case Asc = 1
    // 降序
    case Dsec = 2
};

class Sort<Element : Comparable> {

    // 堆的类型
    fileprivate enum HeapType : Int {
        // 大顶堆
        case Big = 1
        // 小顶堆
        case Small = 2
    };

    // 排序方式
    fileprivate var _sortType : SortType?;

    func heapSort(sortType: SortType){

        // 从外部传入排序方式，升序或降序
        _sortType = sortType;

        // 从最后⼀个⾮叶⼦结点开始，从下往上进⾏调整，最终将无序数列调整为【大/小顶堆】
        for i in (1..._arr.count / 2).reversed() {
            heapAjust(i: i, c: _arr.count);
        }

        // 从最后一个结点开始，与根结点交换，调整
        for c in (2..<_arr.count).reversed() {
            swap(i: 1, j: c);
            heapAjust(i: 1, c: c);
        }
    }

    // 根据【大/小顶堆】的特性，实现比较方法
    fileprivate func compare(curr: Element, target: Element) -> Bool {

        // 升序使用大顶堆，降序使用小顶堆
        let heapType = _sortType == .Asc ? HeapType.Big : HeapType.Small;

        if(heapType == HeapType.Big){
            return curr >= target;
        }

        return curr <= target;
    }

    // 根据【大/小顶堆】的特性，调整结点
    func heapAjust(i: Int, c: Int){

        var j = i;

        while(j < c) {

            // 获取左孩子结点索引值
            let leftIndex = j * 2;

            // 判断是否存在左孩子
            if(leftIndex >= c){
                // 不存在，当前为叶子结点，不需要调整
                break;
            }

            // 准备交换的索引值，默认为左孩子
            var targetIndex = leftIndex;
            // 获取右孩子结点索引值
            let rightIndex = leftIndex + 1;

            // 判断右孩子是否存在，存在则与左孩子对比
            if(rightIndex < c && compare(curr: _arr[rightIndex]!, target: _arr[leftIndex]!)){
                // 存在，并且比左孩子更符合【大/小顶堆】的特性，将准备交换的索引值更新为右孩子
                targetIndex = rightIndex;
            }

            // 根结点与准备交换的结点对比
            if(compare(curr: _arr[j]!, target: _arr[targetIndex]!)){
                // 根结点更符合【大/小顶堆】的特性，不需要调整，结束循环
                break;
            }

            // 否则，需要调整，交换结点值
            swap(i: j, j: targetIndex);
            // 将j赋值为交换的索引值，准备进入下一轮循环
            j = targetIndex;
        }
    }
}

6.4 时间复杂度

堆排序的运⾏时间，主要消耗在初始构建堆和重建的交换与调整上

6.4.1 初始构建堆

初始构建堆：O(n)

推算过程：

假设：⾼度为k，则从倒数第⼆层右边的结点开始，这⼀层的结点都要执⾏⼦结点⽐较然后交换（如果顺序是对的就不⽤交换）。倒数第三层，则会选择其⼦节点进⾏⽐较和交换，如果没交换就可以不⽤再执⾏下去了。如果交换了，那么⼜要选择⼀⽀⼦树进⾏⽐较和交换

那么总的时间计算为：s = 2 ^ (i - 1) * (k - i)。其中i表示第⼏层，2 ^ (i - 1)表示该层上有多少个元素，(k - i)表示⼦树上要⽐较的次数。如果在最差的条件下，就是⽐较次数之后还要交换。因为这个是常数，所以提出来后可以忽略

公式：S = 2 ^ (k - 2) * 1 + 2 ^ (k - 3) * 2 ... + 2 * (k - 2) + 2 ^ (0) * (k - 1)，因为叶⼦层不⽤交换，所以i从k - 1开始到1

这个等式求解，等式左右乘上2，然后和原来的等式相减，就变成了：S = 2 ^ (k - 1) + 2 ^ (k - 2) + 2 ^ (k - 3) ... + 2 - (k - 1)

除最后⼀项外，就是⼀个等⽐数列，直接⽤求和公式：S = {a1[1 - (q ^ n)]} / (1 - q)

S = 2 ^ k - k -1，⼜因为k为完全⼆叉树的深度，所以 (2 ^ k) <= n < (2 ^ k - 1)，可以认为：k = logn（实际计算得到应该是log(n + 1) < k <= logn）

综上所述得到：S = n - longn - 1，所以时间复杂度为：O(n)

6.4.2 交换与调整

更改堆元素后重建堆时间：O(nlogn)

推算过程：

循环n - 1次，每次都是从根节点往下循环查找，所以每⼀次时间是logn

总时间：logn(n - 1) = nlogn - logn

最终堆排序的时间复杂度，取后者。即：O(nlogn)

空间复杂度：堆排序是就地排序，空间复杂度为常数：O(1)

总结

排序的分类：

  • 内排序：是在排序整个过程中，待排序的所有记录全部被放置在内存中

  • 外排序：由于排序的记录个数太多，不能同时放置在内存，整个排序过程需要在内外存之间多次交换数据才能进⾏

冒泡排序（Bubble Sort）：

  • ⼀种交换排序，它的基本思想就是：两两⽐较相邻的记录的关键字，如果反序则交换，直到没有反序的记录为⽌

  • 时间复杂度：O(n ^ 2)

  • 初级版本：并不符合相邻记录两两⽐较的特性。所以严格来说，只是一个交换排序，而非冒泡排序

  • 完成形态：真正的冒泡排序，它在每一次比较中，都会将较小的数据上浮，较大的数据下沉。所以每一次比较，都会对后面其他元素的排序起到帮助

  • 排序优化：定义一个标记，当内层循环触发元素交换，标记就会修改。如果标记未修改，则表示此数列已有序，退出循环即可

简单选择排序（Simple Selecton Sort）：

  • 就是通过n - i次关键词⽐较，从n - i + 1个记录中找出关键字最⼩的记录，并和第i个记录进⾏交换。i的范围：1 <= i <= n

  • 时间复杂度：O(n ^ 2)

直接插⼊排序（Stight Inserton Sort）：

  • 它的基本操作是将⼀个记录插⼊到已经排好序的有序表中，从⽽得到⼀个新的记录数+1的有序表

  • 时间复杂度：O(n ^ 2)

希尔排序（Shell Sort）：

  • 是把记录按下标的⼀定增量分组，对每组使⽤直接插⼊排序算法排序。随着增量逐渐减少，每组包含的关键词越来越多。当增量减⾄1时，整个数列被分成⼀组，算法终⽌

  • 基本有序：它会尽可能做到较大的数据在数列尾部，较小的数据在数列头部。当数列是基本有序的情况下，进行插⼊排序是最高效的

  • 时间复杂度：希尔排序是第一个打破O(n ^ 2)的排序算法，时间复杂度与步⻓序列有关。目前为止，增量序列有一些推荐使用的公式。但如何设计一个最高效的增量序列，仍是未解难题

堆的结构：

  • 堆是具有下⾯性质的完全⼆叉树：

    • 每个结点的值都⼤于或等于其左右孩⼦结点的值，称为⼤顶堆

    • 或者，每个结点的值都⼩于等于其左右孩⼦的结点的值，称为⼩顶堆

堆排序（Heap Sort）：

  • 就是利⽤堆（假设⼤顶堆）进⾏排序的算法，它的基本思想：

    • 将待排序的数列构成⼀个⼤顶堆。此时，整个数列的最⼤值就堆顶的根结点。将它移⾛（其实就是将其与堆数组的末尾元素交换），此时末尾元素就是最⼤值

    • 然后将剩余的n - 1个数列重新构成⼀个堆，这样就会得到n个元素的次⼤值，如此重复执⾏，就能得到⼀个有序数列了

  • 思路分析：

    • 将无序数列构建成⼀个堆，根据升序降序需求选择⼤顶堆或⼩顶堆

    • 将堆顶元素与末尾元素交换，将最⼤元素“沉”到数组末端

    • 重新调整结构，使其满⾜堆定义，然后继续交换堆顶元素与当前末尾元素，反复执⾏调整 + 交换步骤，直到整个数列有序

  • 结点的寻找：

    • 堆具有完全⼆叉树的性质，如果对一棵有n个结点的完全⼆叉树的结点按层序编号，对任⼀结点i（1 <= i <= n）有：

      • 如果i = 1，则结点i是⼆叉树的根，⽆双亲。如果i > 1，则其双亲是结点i / 2

      • 如果2i > n，则结点i⽆左孩⼦（结点i为叶⼦结点），否则左孩⼦是结点2i

      • 如果2i + 1 > n，则结点i⽆右孩⼦，否则其右孩⼦是结点2i + 1

  • 时间复杂度：

    • 初始构建堆：O(n)

    • 更改堆元素后重建堆时间：O(nlogn)

    • 堆排序的时间复杂度，取后者。即：O(nlogn)

  • 空间复杂度：

    • 堆排序是就地排序，空间复杂度为常数：O(1)