1. 图的初识
线性表的特性,相邻数据之间有线性关系,属于前驱或后继结点,具备一对一关系。树结构的特性,相邻结点有层次关系,具备一对多关系。而图结构更为复杂,它的结点之间关系是任意的
1.1 概述
图(Graph) 是由顶点的有穷⾮空集合和顶点之间边的集合组成,图结构中的结点称之为顶点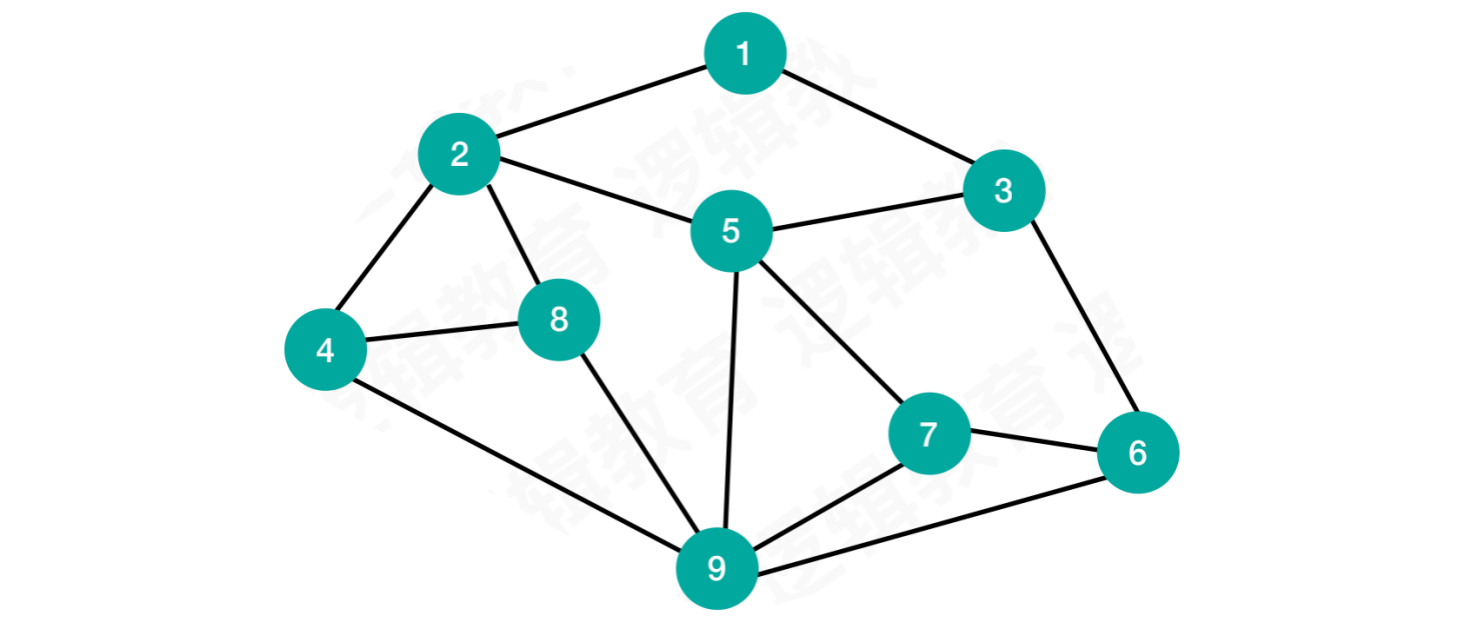
通常表示为
G(V, E)G表示⼀个图V是图G中的顶点集合E是图G中边的集合
线性表中可以没有数据,我们称之为空表。树结构中可以没有结点,我们称之为空树。但是图结构中,不允许没有顶点,也不存在空图一说
图中的任意点都可作为起点,即使两点不相邻,它们之间也可能存在关系
1.2 定义
1.2.1 无向图 & 无向边
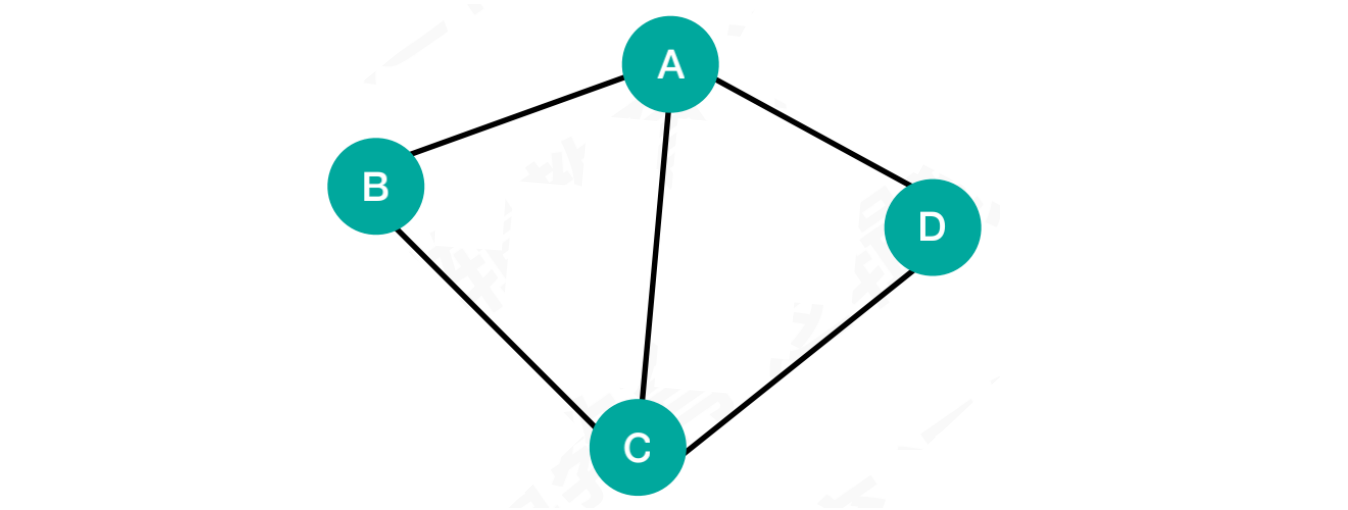
图中
A点和C点相连的边没有箭头指向,表示这条边是没有方向的。这样就可以从A点到C点,也可以从C点到A点,该边被称之为无向边由这些无向边连接的图,称之为无向图
1.2.2 有向图 & 有向边
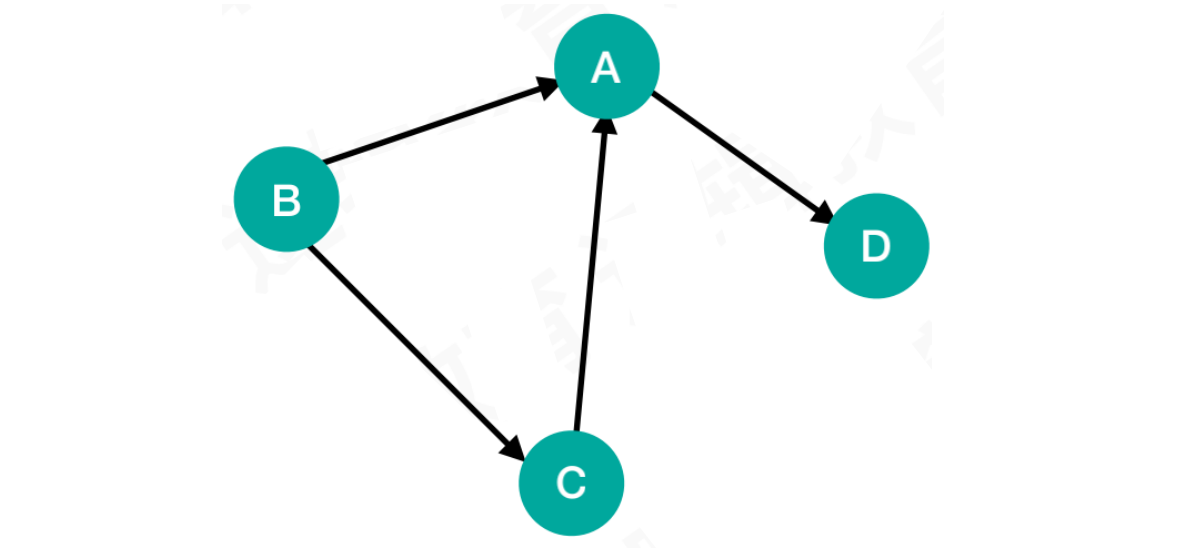
图中
B点和A点相连的边有箭头指向,表示这条边有方向,只允许从B点到A点,该边被称之为有向边由这些有向边连接的图,称之为有向图
1.2.3 无向完全图
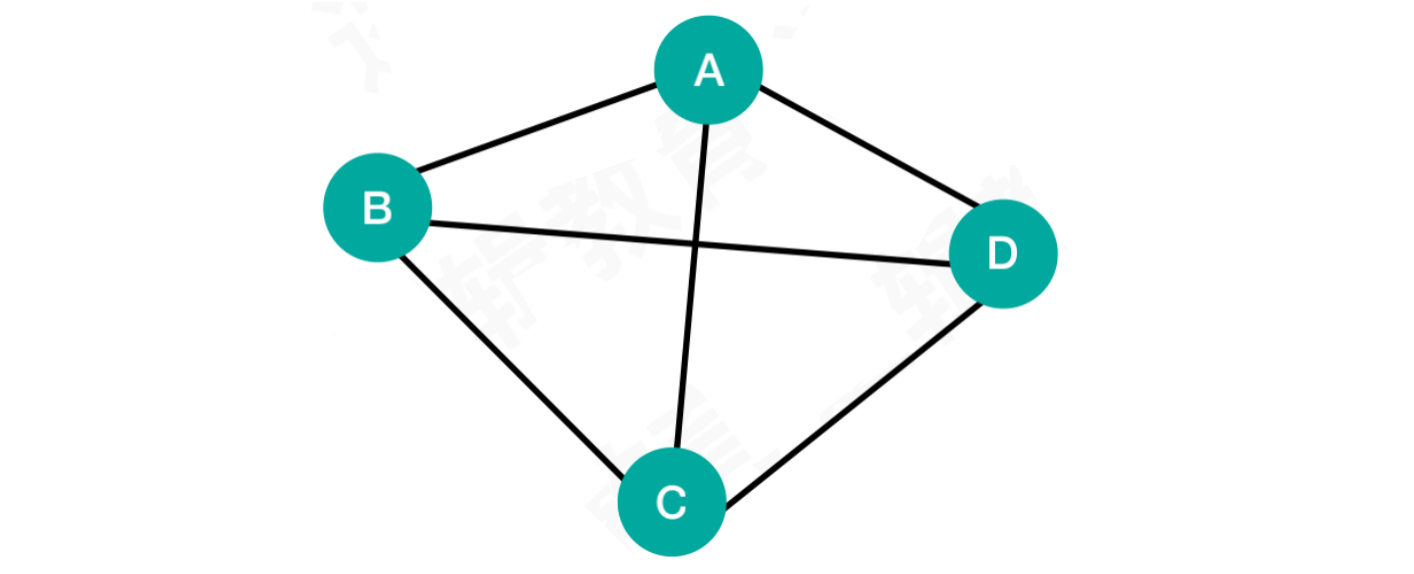
- 某一个点到任意点都被无向边直接连接,称之为无向完全图
1.2.4 有向完全图
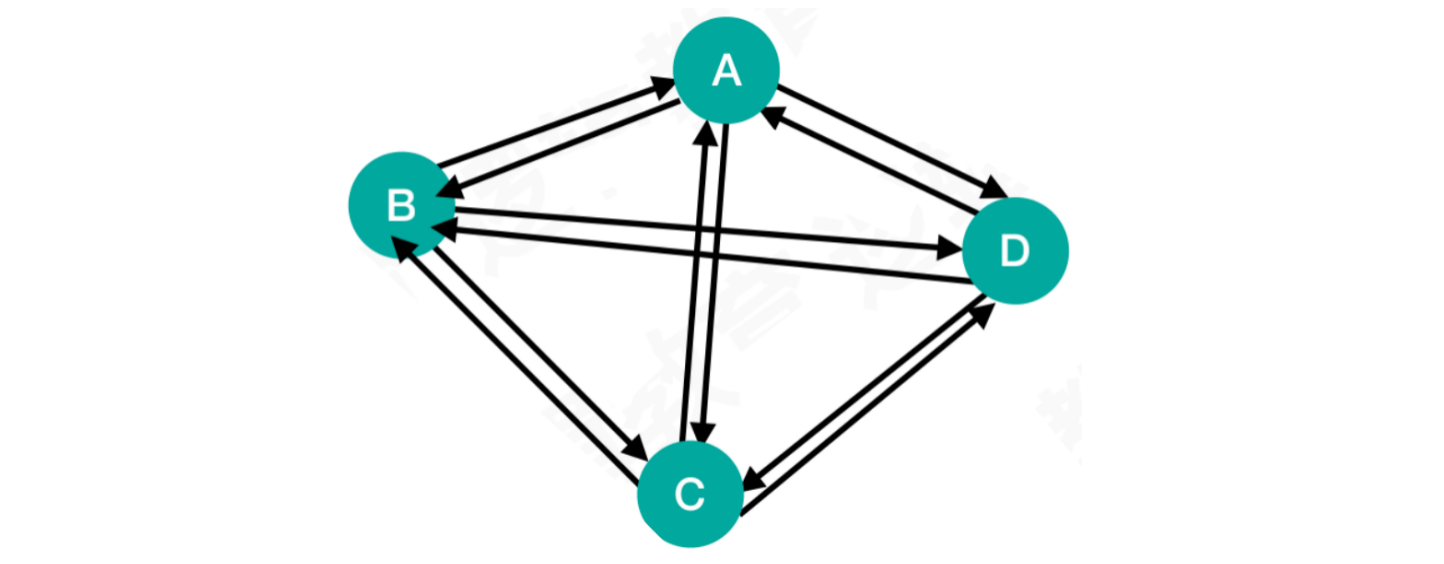
- 某一个点到任意点都被有向边直接连接,并且顶点与顶点之间被双向箭头连接,称之为有向完全图
1.2.5 网
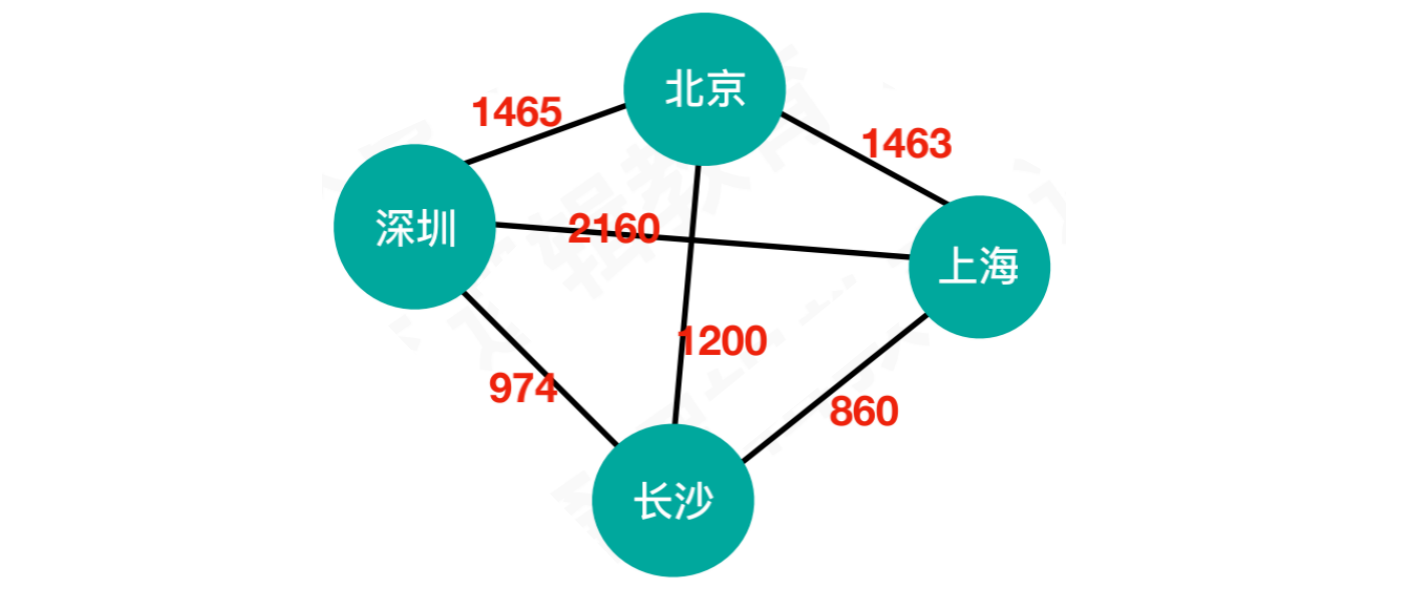
- 顶点与顶点连接带有权值的图,称之为网
1.2.6 子图
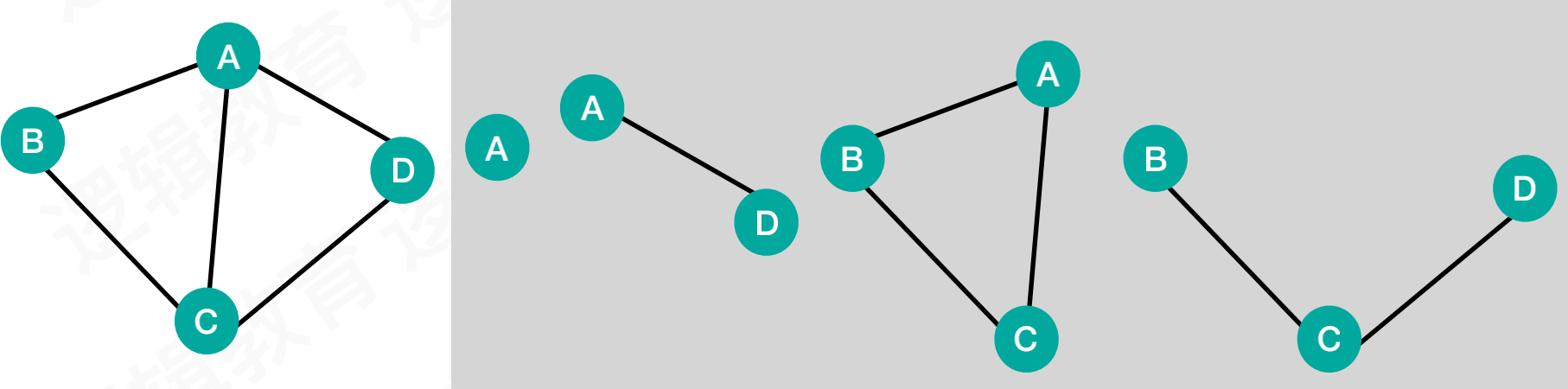
- 从
无向图G中,可以拆分出很多子图
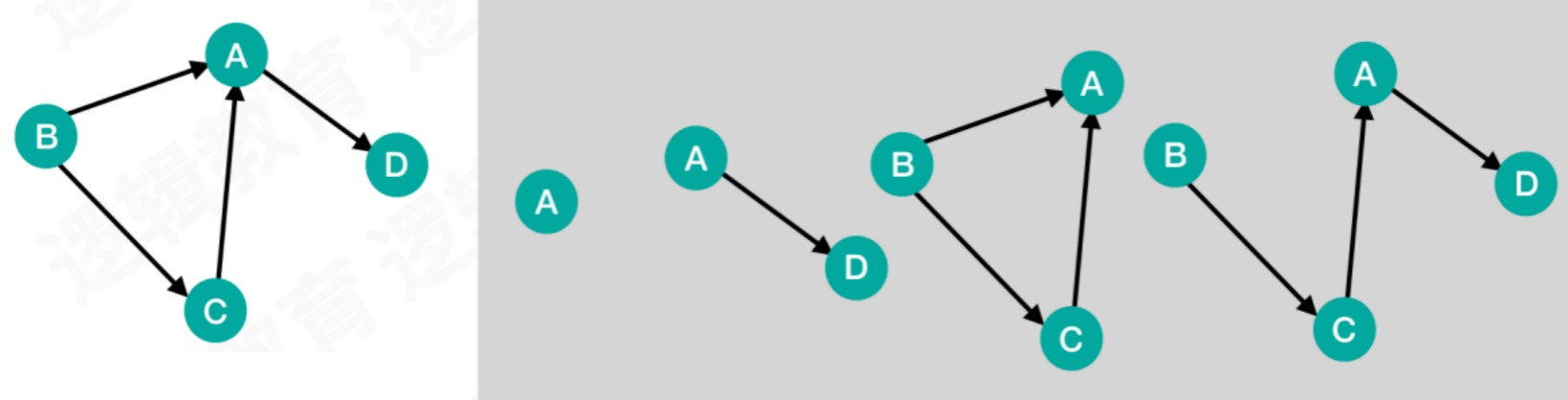
- 在
有向图G中,同样可以拆分子图
1.2.7 环
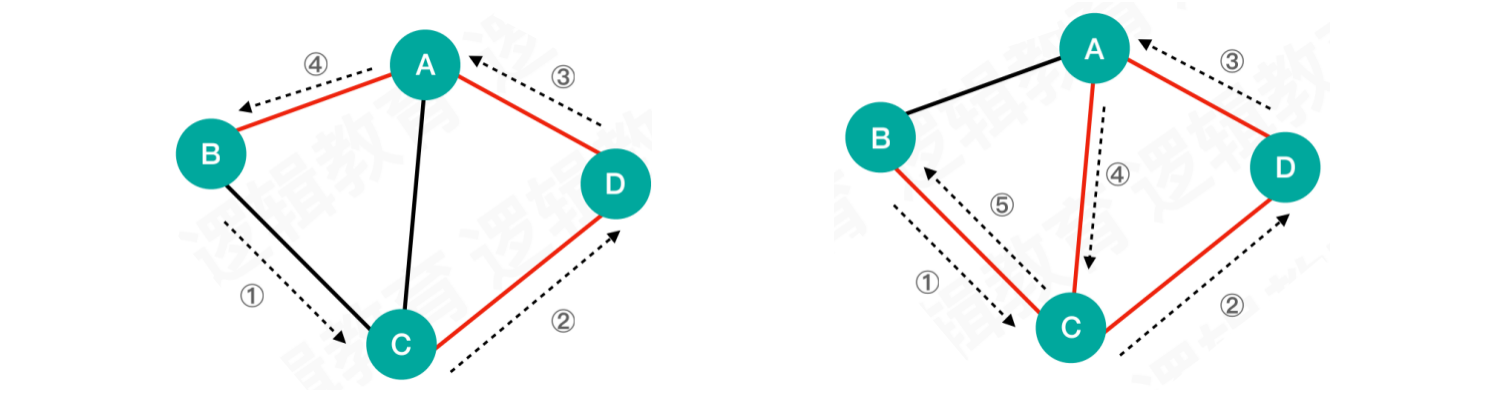
- 从第一个顶点到最后一个顶点之间是闭合的
1.2.8 连通图
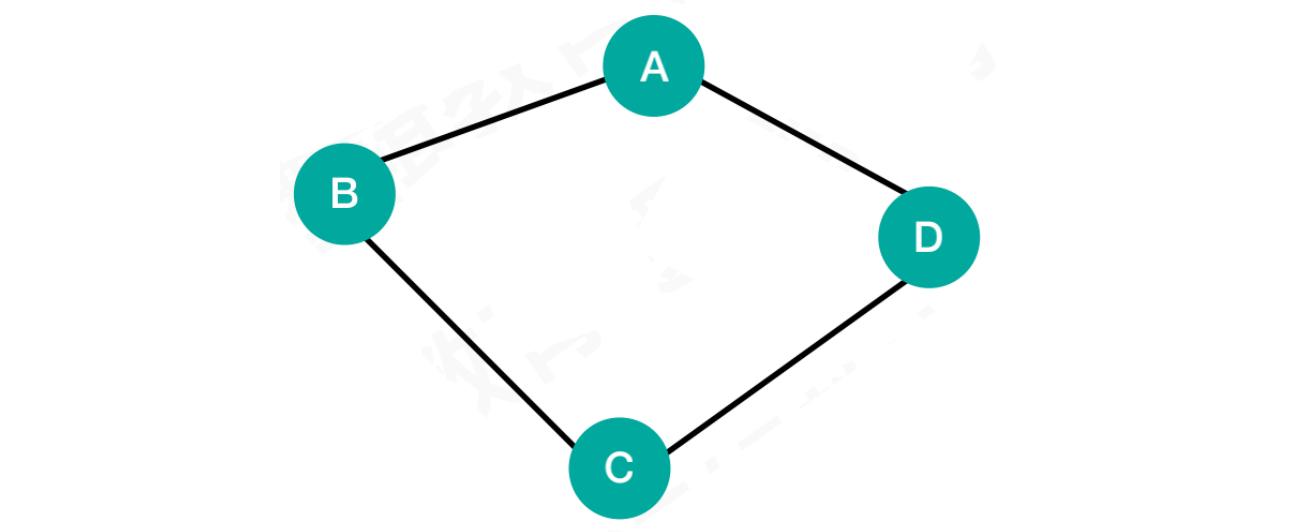
- 图中顶点之间相互都是连通的,称之为连通图
1.2.9 非连通图
以下图中,ABCD与EF之间是不连通的,所以该图属于非连通图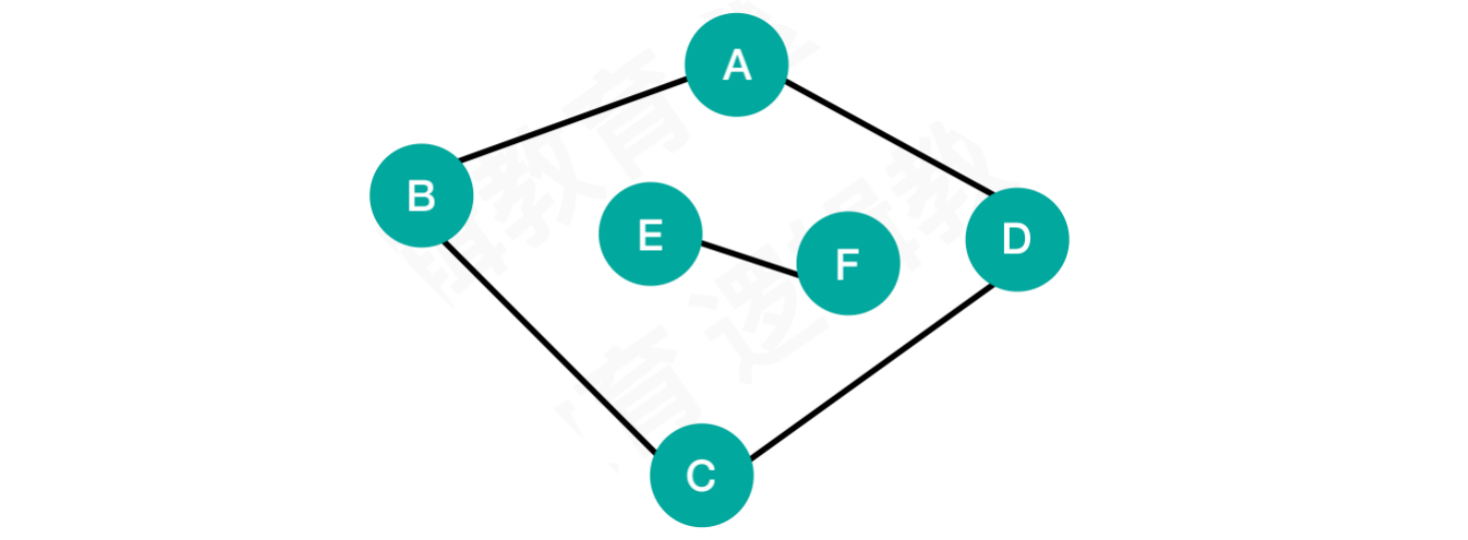
2. 图的存储
任何逻辑结构的存储,最终都会采用链式存储,或顺序存储。图的存储也不例外
图的两个特点,顶点和边。我们通过顶点和边的连接,可以确定图的逻辑关系。所以图的存储,需要考虑顶点的存储,以及边与边的连接信息
所谓“边”,就是两点之间连接的线。在无向图中称之为“边”,在有向图中称之为“弧”
2.1 图的邻接矩阵存储
邻接矩阵存储,本质上就是采用顺序存储,将图的逻辑进行存储
采用顺序存储,将顶点和边一起存储会相对困难,因为它们存在多对对的关系。所以我们可以将顶点和边分开存储
示例:将以下图存储到计算机中,请设计⼀个数据结构并将其合理存储起来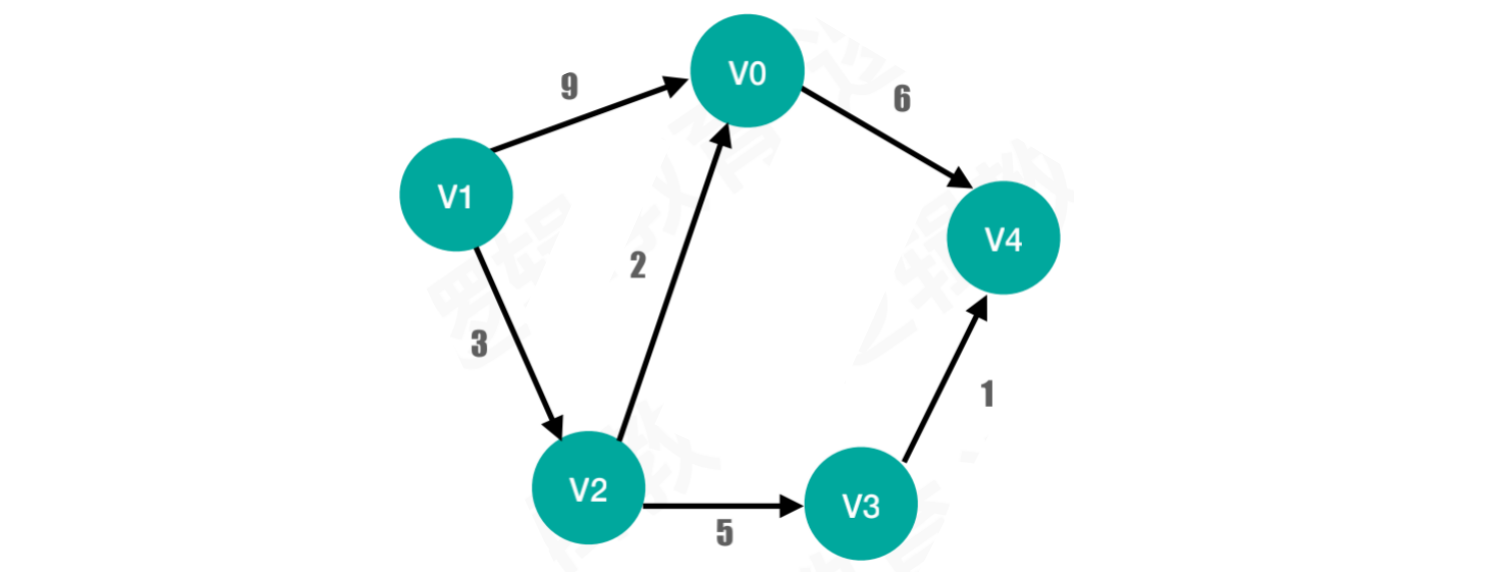
图中的顶点可以直接使用一维数组存储
而连接关系,使用二维数组,和顶点分开存储
案例1:无向图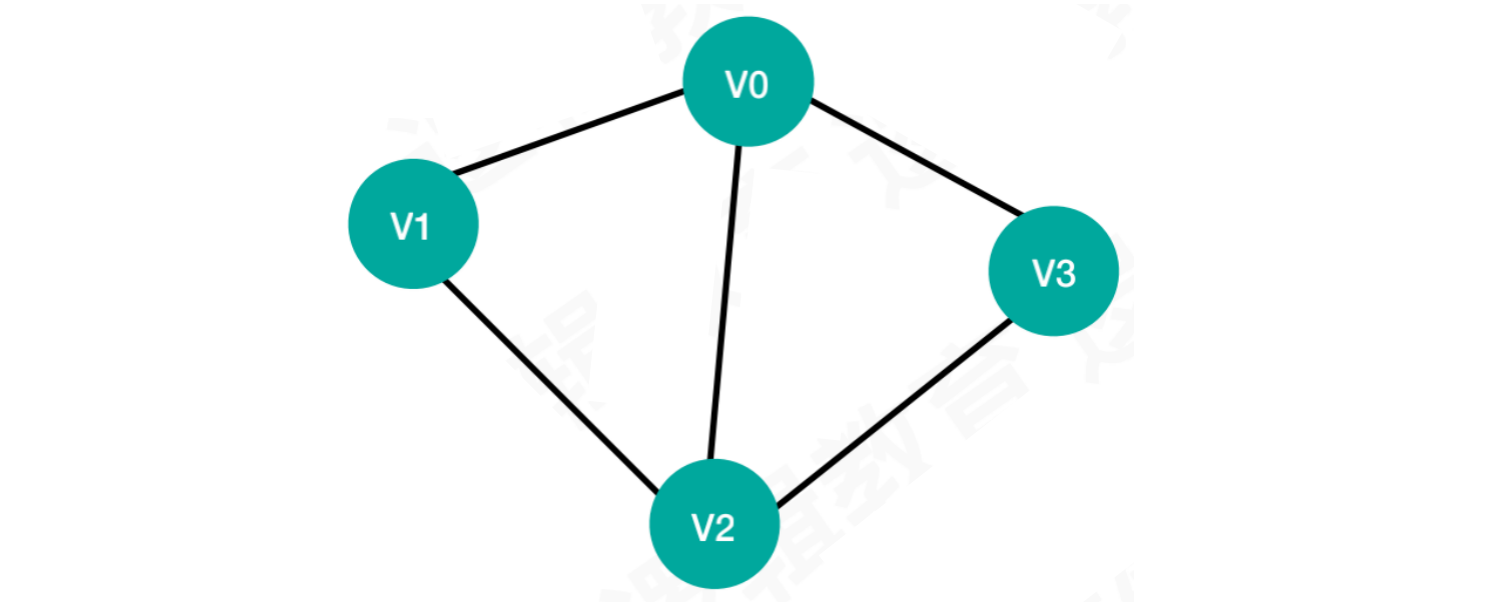
设图G有n个顶点,则邻接矩阵是⼀个n * n的⽅阵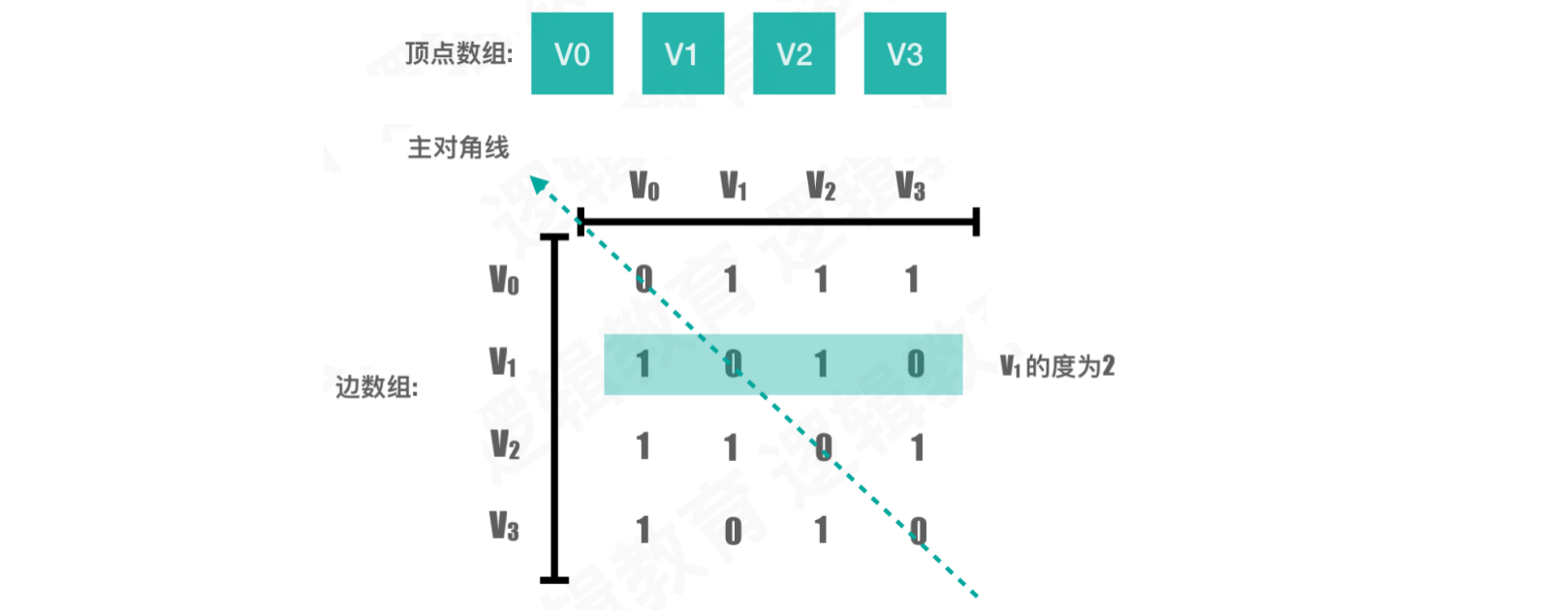
若两点之间有连接,表示为
1,否则为0对角线的位置一定为
0因为是无向图,横向和纵向存储的数据是对称的
顶点的度,是指邻接矩阵第
i行,或第j列,非0元素的总和如果
arc[i][j]值为1,表示顶点i和顶点j存在连接关系
案例2:有向图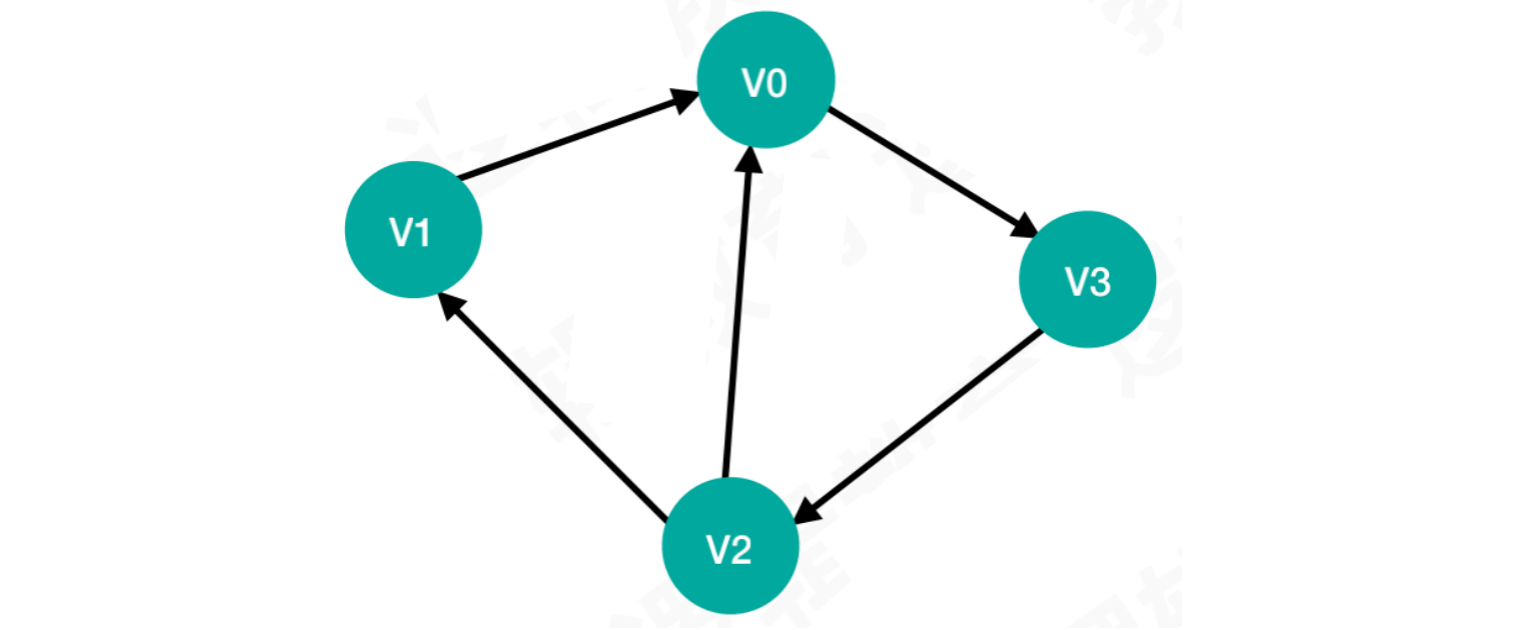
由于两点之间的连接是单向的,所以横向和纵向存储的数据是不对称的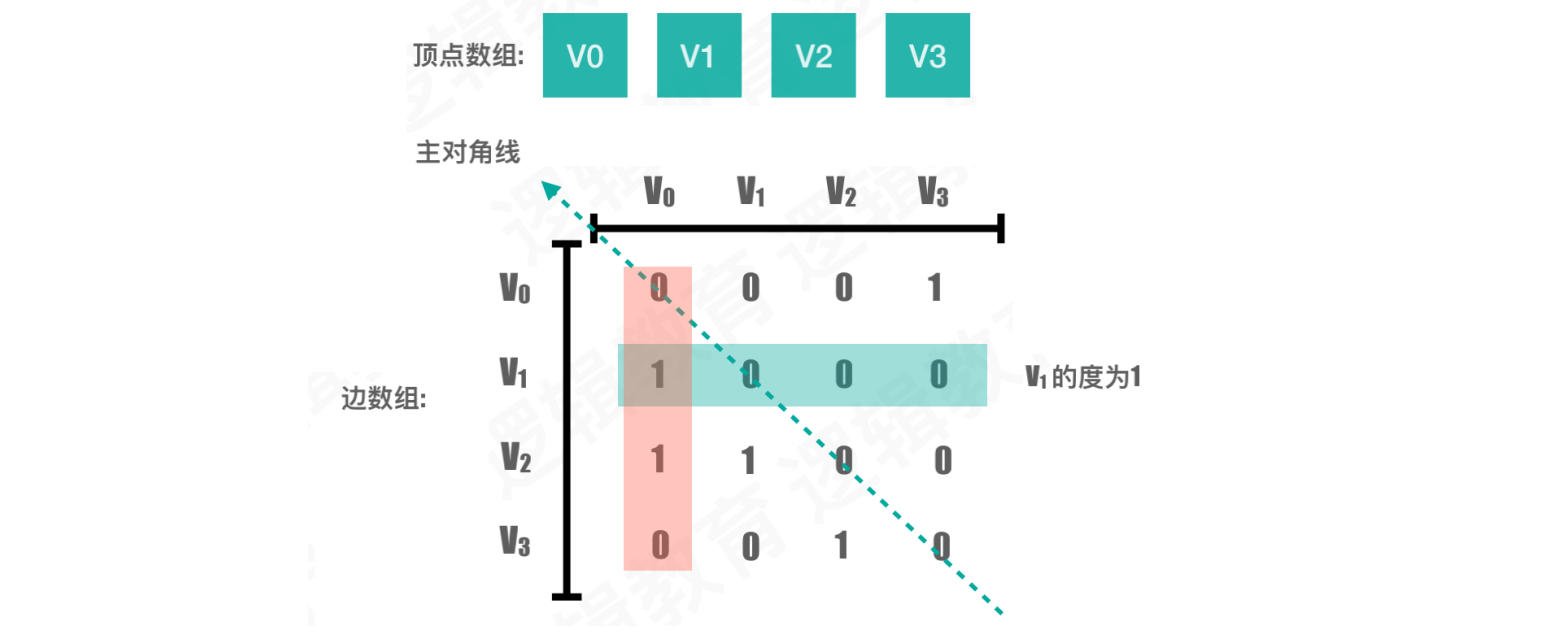
- 顶点无法直接到达另一个顶点的位置都为
0
案例3:网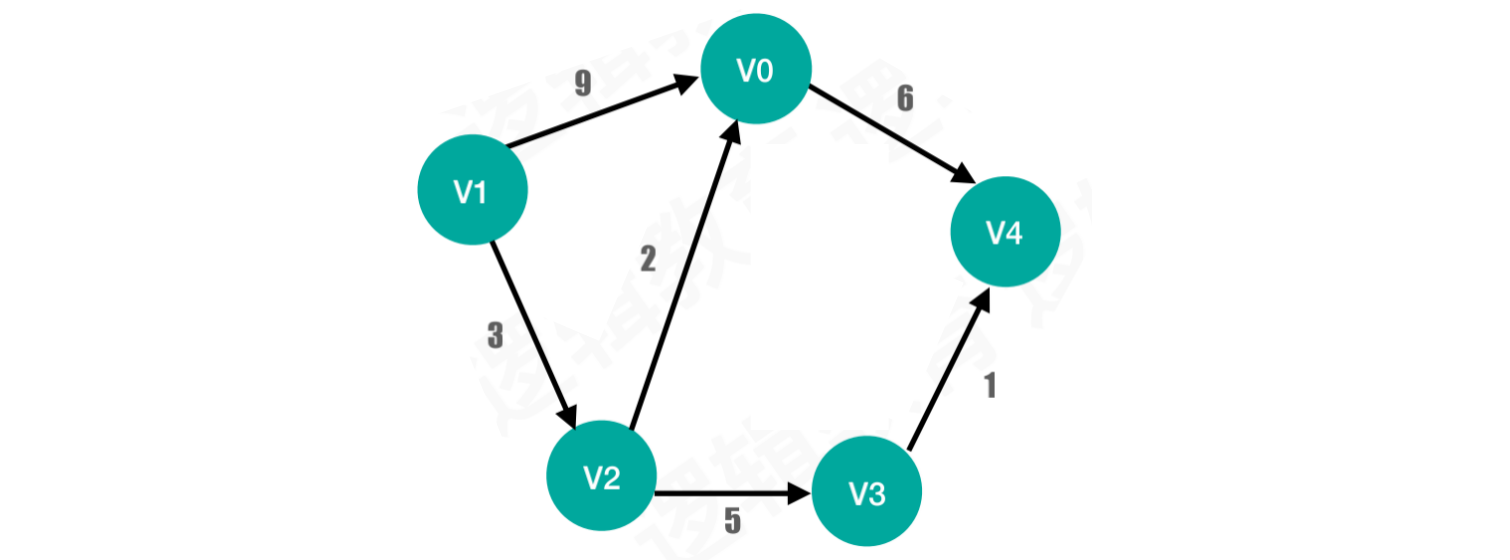
只有当i == j时为0,也就是对角线位置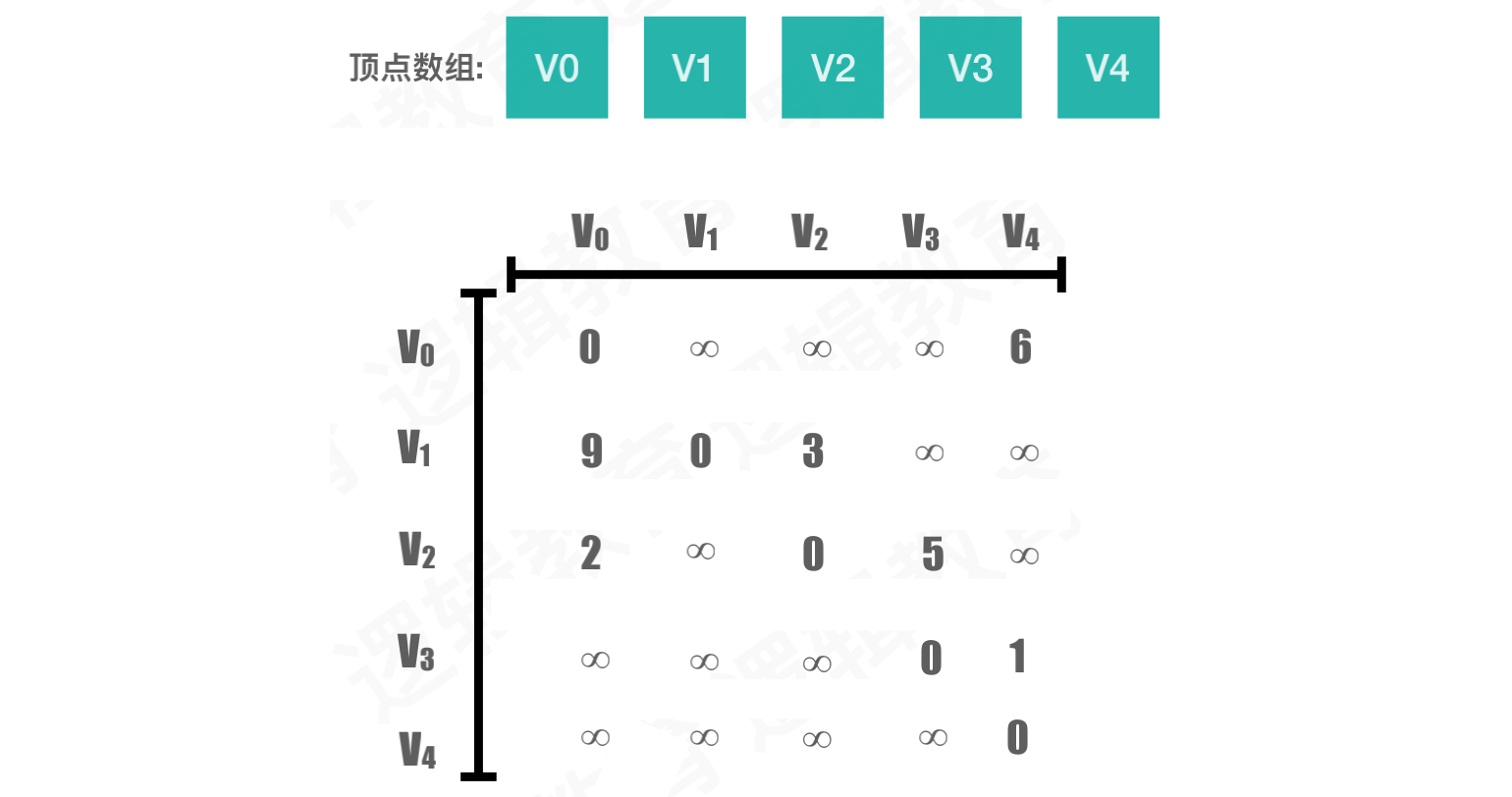
顶点直接到达另一个顶点,该位置填充权值
对角线位置为
0否则为∞,表示没有连接关系。在代码中,则使用
Int.max表示
2.1.1 数据结构设计
class MGraph {var vexs : [String]?;var arc : [[Int]]?;var numNodes : Int;var numEdges : Int;}
vexs:顶点表arc:邻接矩阵,相当于边表numNodes:顶点数numEdges:边数
2.1.2 邻接矩阵存储
以无向图为例: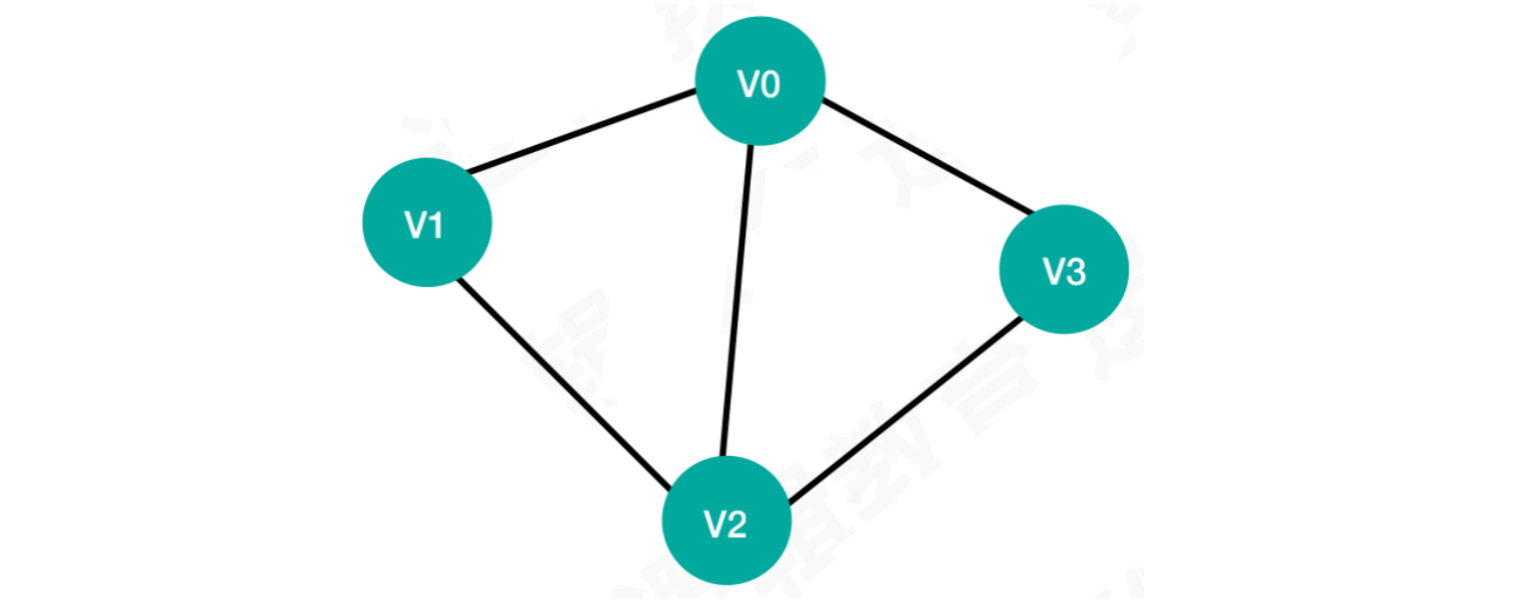
代码实现:
class MGraphLinear {
fileprivate class MGraph {
var vexs : [String]?;
var arc : [[Int]]?;
var numNodes : Int;
var numEdges : Int;
init(){
self.numNodes = 0;
self.numEdges = 0;
}
}
fileprivate var graph : MGraph;
init(){
self.graph = MGraph();
}
func create(nodes : [String], edges : [[Int]], isUndirected : Bool){
self.graph.numNodes = nodes.count;
self.graph.numEdges = edges.count;
self.graph.vexs = [String]();
for node in nodes {
self.graph.vexs?.append(node);
}
self.graph.arc = [[Int]].init(repeating: [Int].init(repeating: 0, count: self.graph.numNodes), count: self.graph.numNodes);
for edge in edges {
let i = edge[0];
let j = edge[1];
let w = edge[2];
self.graph.arc![i][j] = w;
if(isUndirected){
self.graph.arc![j][i] = self.graph.arc![i][j];
}
}
}
}
打印邻接矩阵:
class MGraphLinear {
func traverse() -> String {
var str : String = "";
for arr in self.graph.arc! {
for w in arr {
str += "\(w) "
}
str += "\n";
}
return str;
}
}
创建邻接矩阵:
let nodes = ["A", "B", "C", "D"];
let edges = [[0, 3 ,1], [1, 0, 1], [2, 1, 1], [2, 0, 1], [3, 2, 1]];
let isUndirected = true;
let graphLinear = MGraphLinear();
graphLinear.create(nodes: nodes, edges: edges, isUndirected: isUndirected);
print(graphLinear.traverse());
nodes:创建四个顶点edges:创建五条边信息。索引0表示vi,索引1表示vj,索引2表示权值isUndirected:是否为无向图
打印结果:
0 1 1 1
1 0 1 0
1 1 0 1
1 0 1 0
2.2 图的邻接表存储
使用邻接矩阵存储图,最大的弊端就是空间浪费。例如: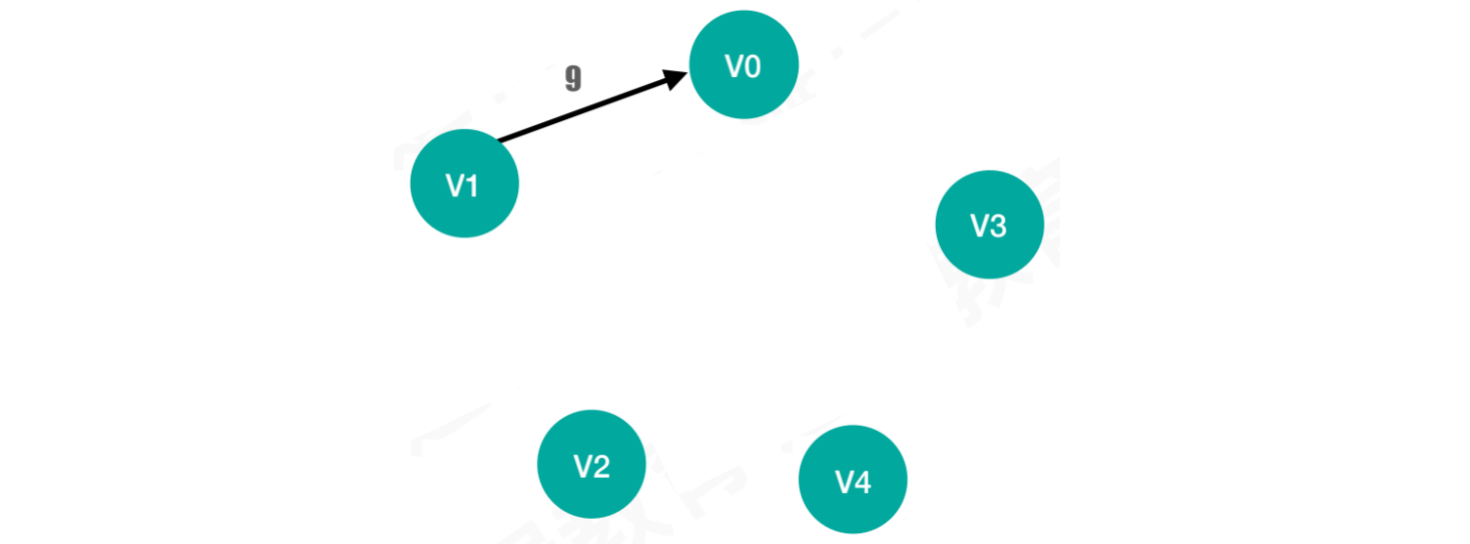
以上图中存在五个顶点,但只有v1到v0存在有向边。使用邻接矩阵存储,大部分空间都是浪费的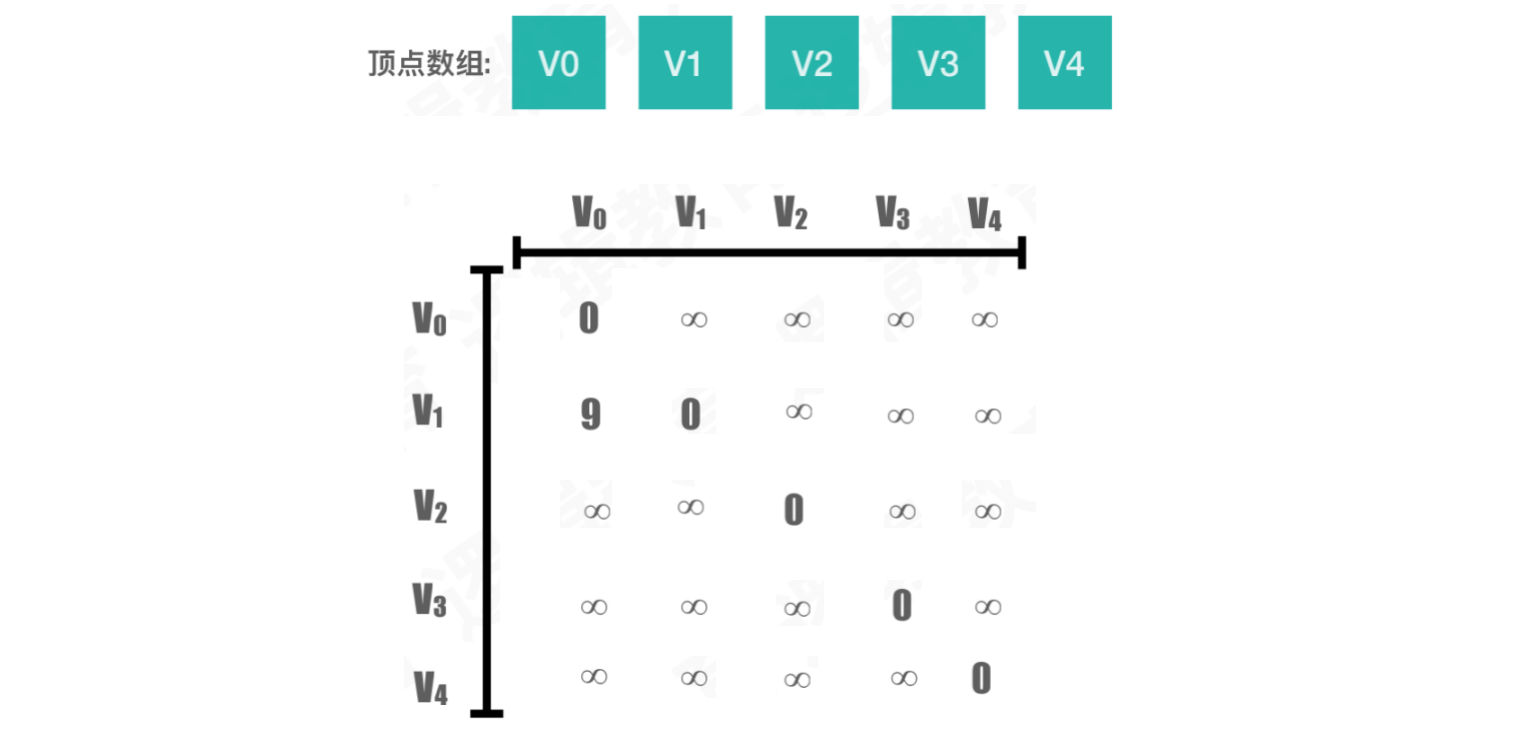
使用邻接表存储,本质上就是采用链式存储,它可以避免空间浪费的问题
案例1:无向图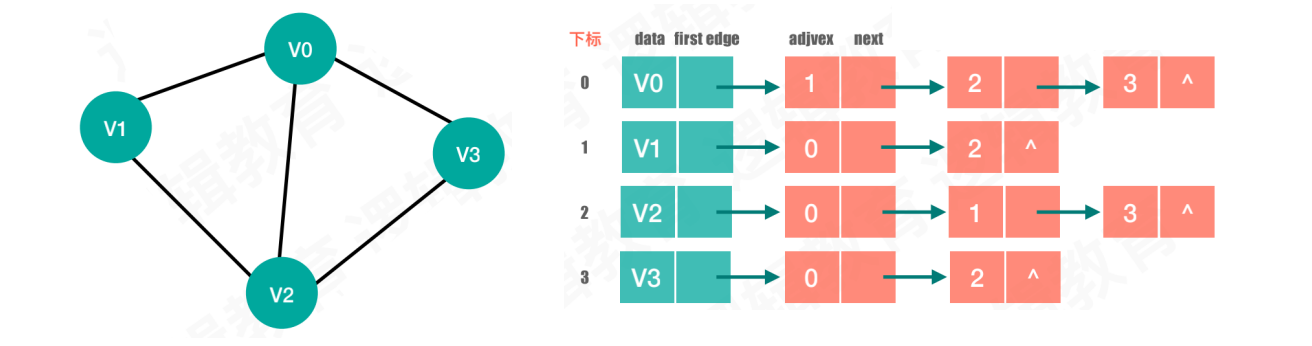
使用一维数组存储所有顶点,数组中的每一个顶点结点,都可以连接它的边表结点,从而形成一条链表
顶点元素的数据结构,存在数据域和指针域。数据域存储顶点信息,指针域指向边表中的第一个结点,相当于链表中的头结点
边表结点的数据结构,存在邻接点域和指针域。邻接点域存储邻接点信息,指针域指向和顶点有关系的下一个邻接点
由于图中顶点之间是无序的,所以顶点和邻接点的连接也没有固定的顺序
获取一个顶点的度,就是它所对应的链表长度
判断
vi和vj是否存在连接关系,需要进行链表的遍历
案例2:有向图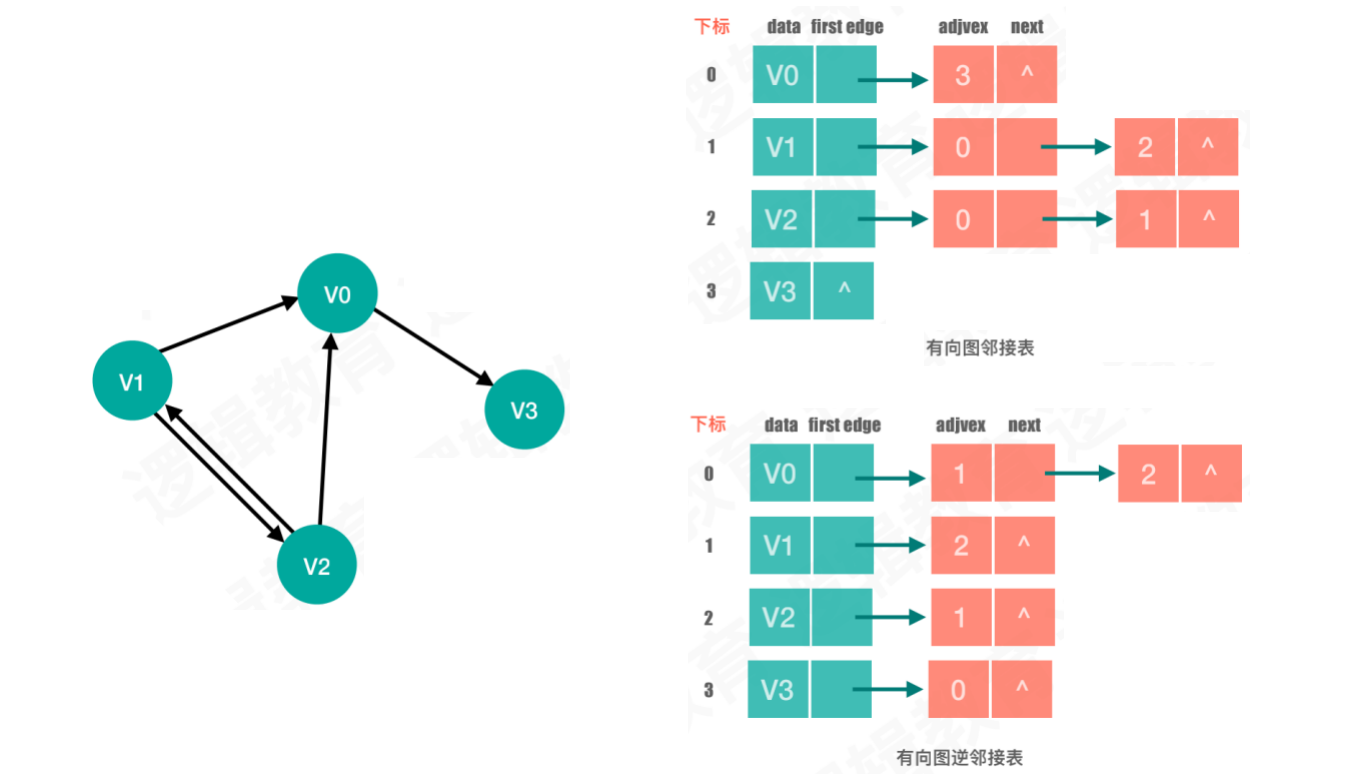
有向图的邻接表中,顶点和邻接点的连接关系仅取决于箭头方向
链表中,将箭头方向相反的顶点进行连接,就会形成逆邻接表
案例3:网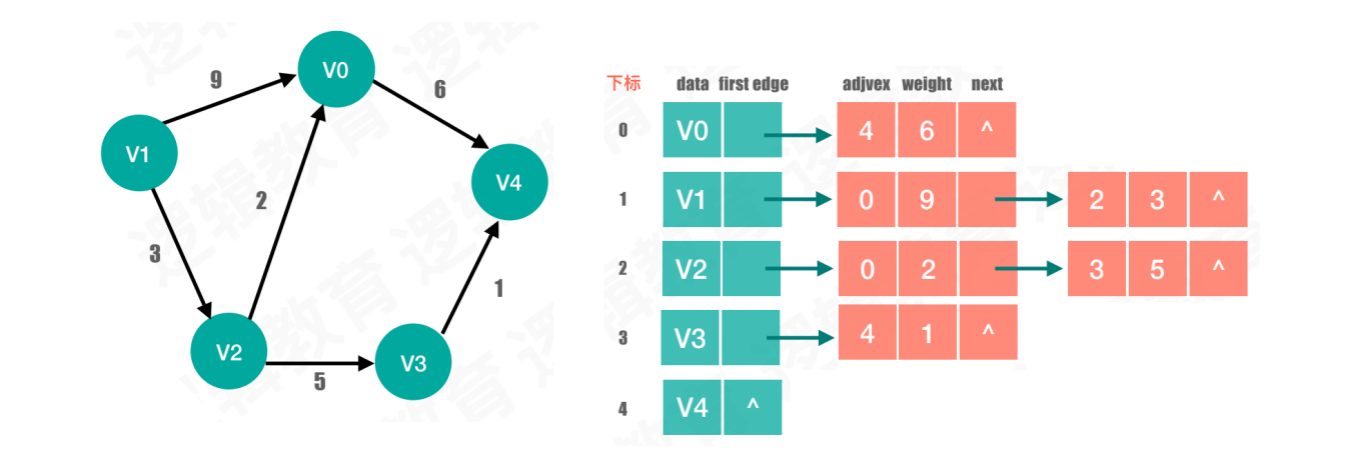
- 网中结点间有权值,所以我们要在边表结点的数据结构中,增加权值的存储
2.2.1 数据结构设计
邻接表结点的数据结构:
class Node {
var adj_vex_index : Int?;
var data : String?;
var node : Node?;
}
adj_vex_index:弧头的下标,也就是被指向的下标。有向图中称之为“弧”,无向图中称之为“边”data:权重值node:边指针
顶点的数据结构:
class VNode {
var data : String?;
var firstEdge : Node?;
}
data:顶点的权值firstEdge:指向边表中的第一个结点
总图的信息:
class Graph {
var adjList : [VNode]?;
var arc_num : Int;
var node_num : Int;
var is_directed : Bool;
}
adjList:顶点表arc_num:边的个数node_num:结点个数is_directed:是否为有向图
2.2.2 邻接表存储
以无向图为例: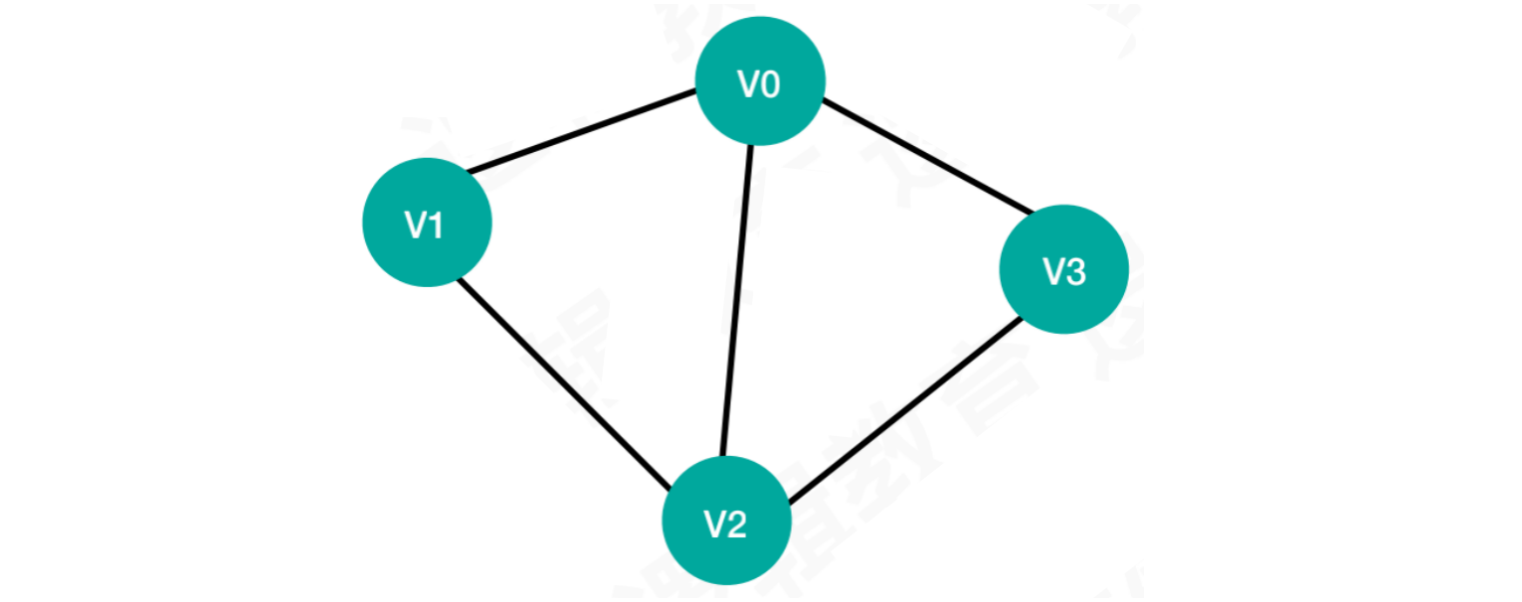
代码实现:
class MGraphLinked {
fileprivate class Node {
var adj_vex_index : Int?;
var data : String?;
var next : Node?;
}
fileprivate class VNode {
var data : String?;
var firstEdge : Node?;
}
fileprivate class Graph {
var adjList : [VNode]?;
var arc_num : Int;
var node_num : Int;
var is_directed : Bool;
init(){
self.arc_num = 0;
self.node_num = 0;
self.is_directed = false;
}
}
fileprivate var graph : Graph;
init(){
self.graph = Graph();
}
func create(nodes : [String], arcs : [[Int]], isUndirected : Bool) {
self.graph.arc_num = arcs.count;
self.graph.node_num = nodes.count;
self.graph.is_directed = !isUndirected;
self.graph.adjList = [VNode]();
for data in nodes {
let vNode = VNode();
vNode.data = data;
self.graph.adjList?.append(vNode);
}
for arc in arcs {
let i = arc[0];
let j = arc[1];
let node = Node();
node.adj_vex_index = j;
node.data = self.graph.adjList![j].data;
let vNode = self.graph.adjList![i];
node.next = vNode.firstEdge;
vNode.firstEdge = node;
if(!self.graph.is_directed){
let node = Node();
node.adj_vex_index = i;
node.data = self.graph.adjList![i].data;
let vNode = self.graph.adjList![j];
node.next = vNode.firstEdge;
vNode.firstEdge = node;
}
}
}
}
- 由于被指向的顶点之间没有顺序关系,这里选择更简单的头插法实现连接
打印邻接表:
class MGraphLinked {
func traverse() -> String {
var str : String = "";
for vNode in self.graph.adjList! {
var node = vNode.firstEdge;
while(node != nil){
str += "\(vNode.data!) -> \(node!.data!),";
node = node?.next;
}
str += "\n";
}
return str;
}
}
创建邻接表:
let nodes = ["V0", "V1", "V2", "V3"];
let arcs = [[0, 1], [0, 2], [0, 3], [1, 2], [2, 3]];
let isUndirected = true;
let graphLinked = MGraphLinked();
graphLinked.create(nodes: nodes, arcs: arcs, isUndirected: isUndirected);
print(graphLinked.traverse());
nodes:创建四个顶点arcs:创建五条边信息。索引0表示当前顶点下标,索引1表示弧头的下标,也就是被指向的下标isUndirected:是否为无向图
打印结果:
V0 -> V3,V0 -> V2,V0 -> V1,
V1 -> V2,V1 -> V0,
V2 -> V3,V2 -> V1,V2 -> V0,
V3 -> V2,V3 -> V0,
3. 图的遍历
图的遍历是指:从给定图中任意指定的顶点(称为初始点)出发,按照某种搜索方法沿着图的边访问图中的所有顶点,使每个顶点仅被访问一次
图的遍历和树的遍历有些相似,由于图没有层次关系,会比树的遍历又复杂许多
例如: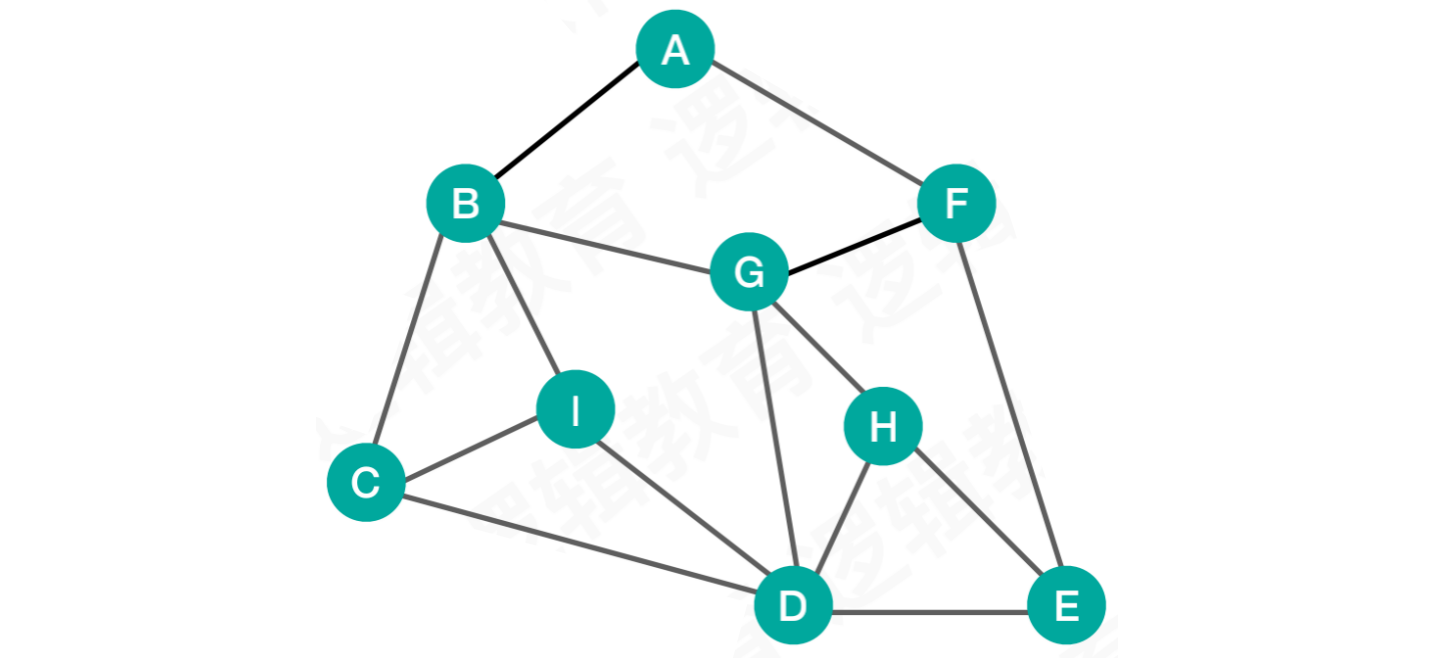
图中任意顶点之间都会存在连接关系,我们从初始点出发,在按照某种路线的遍历过程中,很有可能返回至已访问的顶点上。为了避免这种情况,我们要对访问过的顶点进行标记
除此之外,在遍历过程中,我们要采用科学的遍历方法,从而避免线路的死循环
所以图的遍历,科学遍历方法可以划分为以下两种策略:
深度优先遍历(
DFS,Depth First Search)广度优先遍历(
BFS,Breadth First Search)
3.1 深度优先遍历
深度优先遍历的思想:假设初始状态是图中所有顶点均未被访问,则从某个顶点v出发,首先访问该顶点,然后依次从它的各个未被访问的邻接点出发深度优先搜索遍历图,直至图中所有和v有路径相通的顶点都被访问到。若此时尚有其他顶点未被访问到,则另选一个未被访问的顶点作起始点,重复上述过程,直至图中所有顶点都被访问到为止
例如: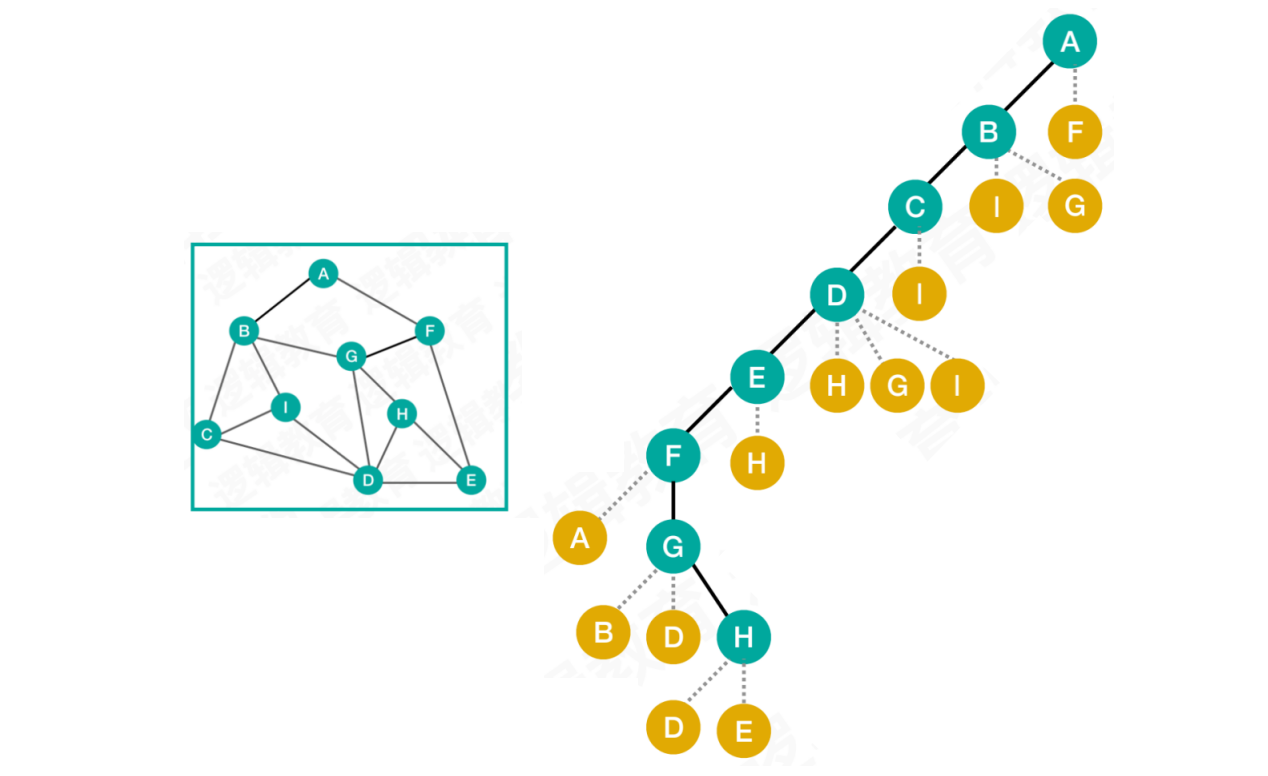
从
顶点A出发,未被访问的邻接点有B和F,遵循右手原则,选择顶点B从
顶点B出发,有C、I、G三种选择,选择顶点C从
顶点C出发,有D、I两种选择,选择顶点D从
顶点D出发,有E、H、G、I四种选择,选择顶点E从
顶点E出发,有F、H两种选择,选择顶点F从
顶点F出发,有A、G两种选择,由于顶点A已被访问,选择顶点G从
顶点G出发,有B、D、H三种选择,由于B、D已被访问,选择顶点H从
顶点H出发,有D、E两种选择,由于D、E均被访问,遍历结束
按照这种遍历路径,我们会发现顶点I并没有被访问。但此时顶点H无路可走,只能进行回退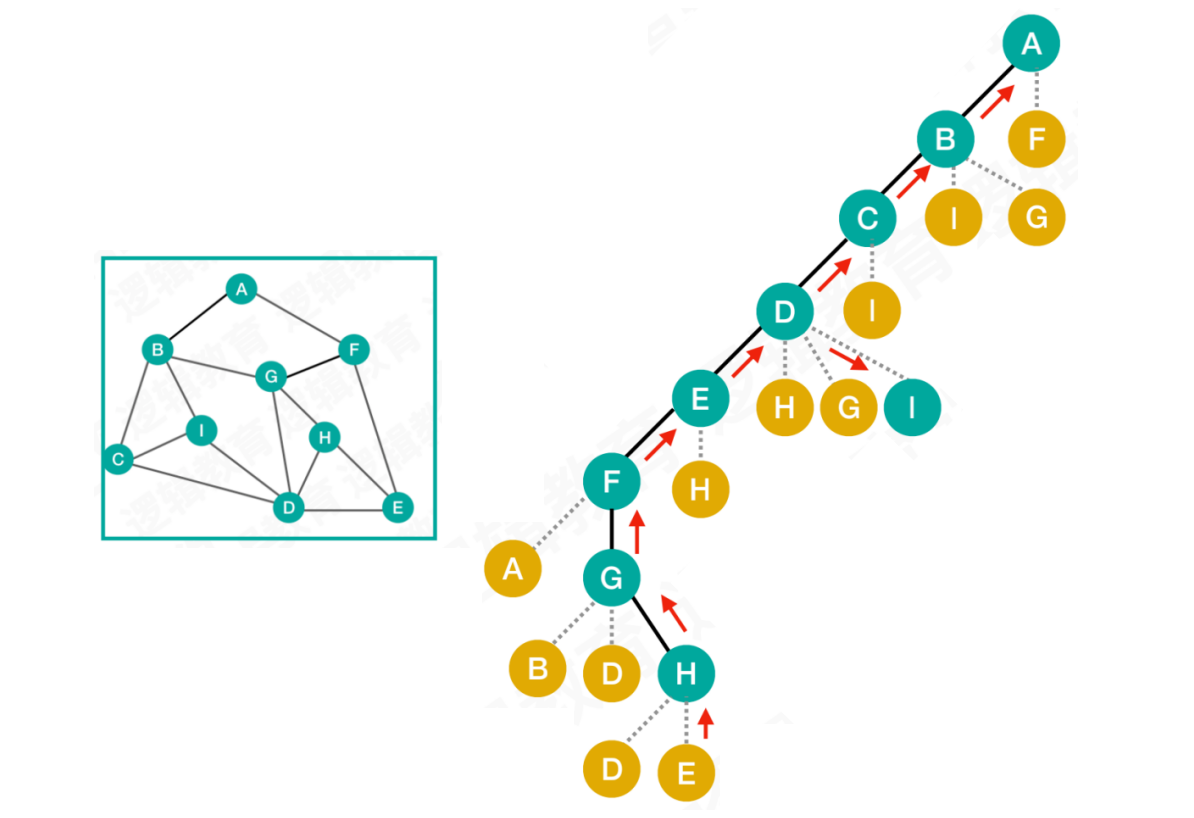
从
顶点H出发,回退到顶点G,继续判断是否存在未被访问的邻接点,如果没有,则继续回退依次从
H→G→F→E回退到顶点D,发现存在未被访问的邻接点I从
顶点I出发,由于没有未被访问的邻接点,继续回退到顶点D依次从
I→D→C→B回退到顶点A,经过一轮完整的回退,完成了所有顶点的访问
3.1.1 邻接矩阵遍历
采用邻接矩阵,实现图的深度优先遍历: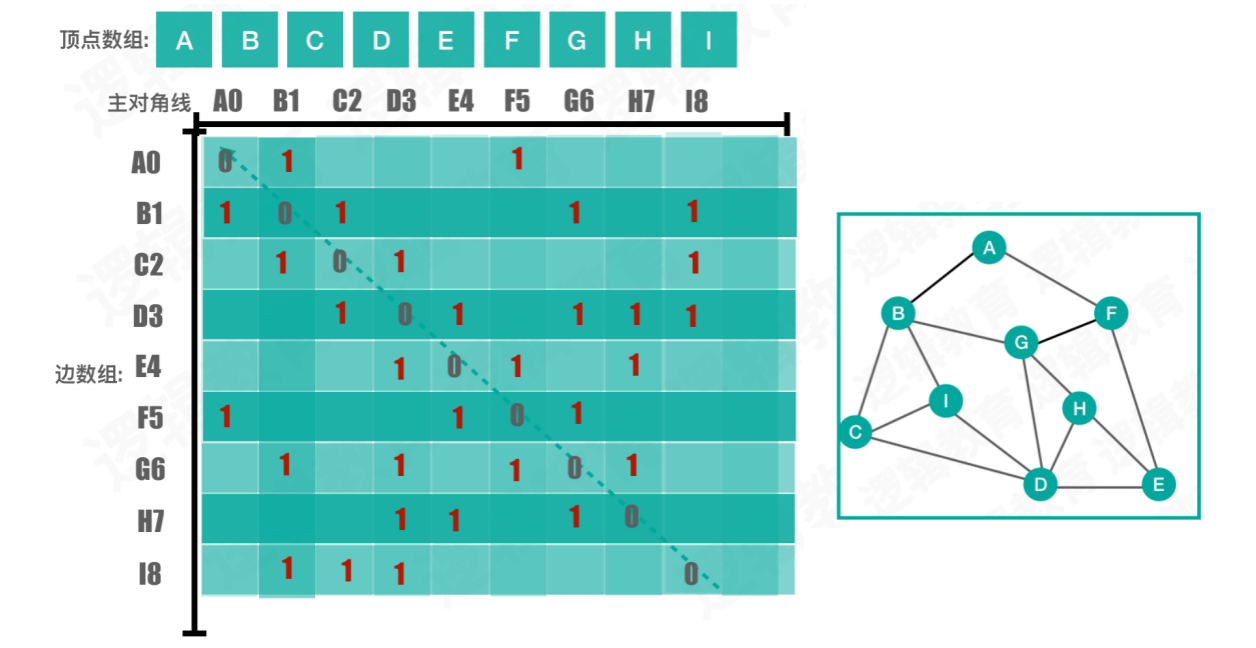
延用上述“邻接矩阵存储”的案例代码,在MGraphLinear类中增加以下代码:
class MGraphLinear {
var visited : [Int]?;
func DFSTraverse() -> String {
var str : String = "";
self.visited = [Int].init(repeating: 0, count: self.graph.numNodes);
for i in 0 ..< self.graph.numNodes {
if(self.visited![i] == 1){
continue;
}
DFS(str: &str, i: i);
}
return str;
}
fileprivate func DFS(str : inout String, i : Int){
self.visited![i] = 1;
str += "\(self.graph.vexs![i]),";
for j in 0 ..< self.graph.numNodes {
if(self.graph.arc![i][j] == 0 || self.visited![j] == 1){
continue;
}
DFS(str: &str, i: j);
}
}
}
创建
visited数组,用来标记顶点是否已被访问根据顶点总数初始化
visited数组,默认未访问遍历顶点信息,如果该顶点未访问,调用
DFS方法进行深度优先遍历- 这一层循环的目的,为了解决非连通图中,未连接的顶点遍历
进入
DFS方法,将当前顶点标记为已访问遍历顶点信息
如果边表中
[i][j]位置为0,表示两个顶点之间未连接,跳过循环如果该顶点已被访问,跳过循环
否则,继续递归
DFS方法
创建邻接矩阵,完成深度优先遍历:
let nodes = ["A", "B", "C", "D", "E", "F", "G", "H", "I"];
let edges = [[0, 1 ,1], [0, 5, 1],
[1, 2, 1], [1, 6, 1], [1, 8, 1],
[2, 3, 1], [2, 8, 1],
[3, 4, 1], [3, 6, 1], [3, 7, 1], [3, 8, 1],
[4, 5, 1], [4, 7, 1],
[5, 6, 1],
[6, 7, 1]];
let isUndirected = true;
let graphLinear = MGraphLinear();
graphLinear.create(nodes: nodes, edges: edges, isUndirected: isUndirected);
print(graphLinear.traverse());
print("深度优先遍历:\(graphLinear.DFSTraverse())");
-------------------------
//输出以下内容:
0 1 0 0 0 1 0 0 0
1 0 1 0 0 0 1 0 1
0 1 0 1 0 0 0 0 1
0 0 1 0 1 0 1 1 1
0 0 0 1 0 1 0 1 0
1 0 0 0 1 0 1 0 0
0 1 0 1 0 1 0 1 0
0 0 0 1 1 0 1 0 0
0 1 1 1 0 0 0 0 0
深度优先遍历:A,B,C,D,E,F,G,H,I,
3.1.2 邻接表遍历
采用邻接表,实现图的深度优先遍历: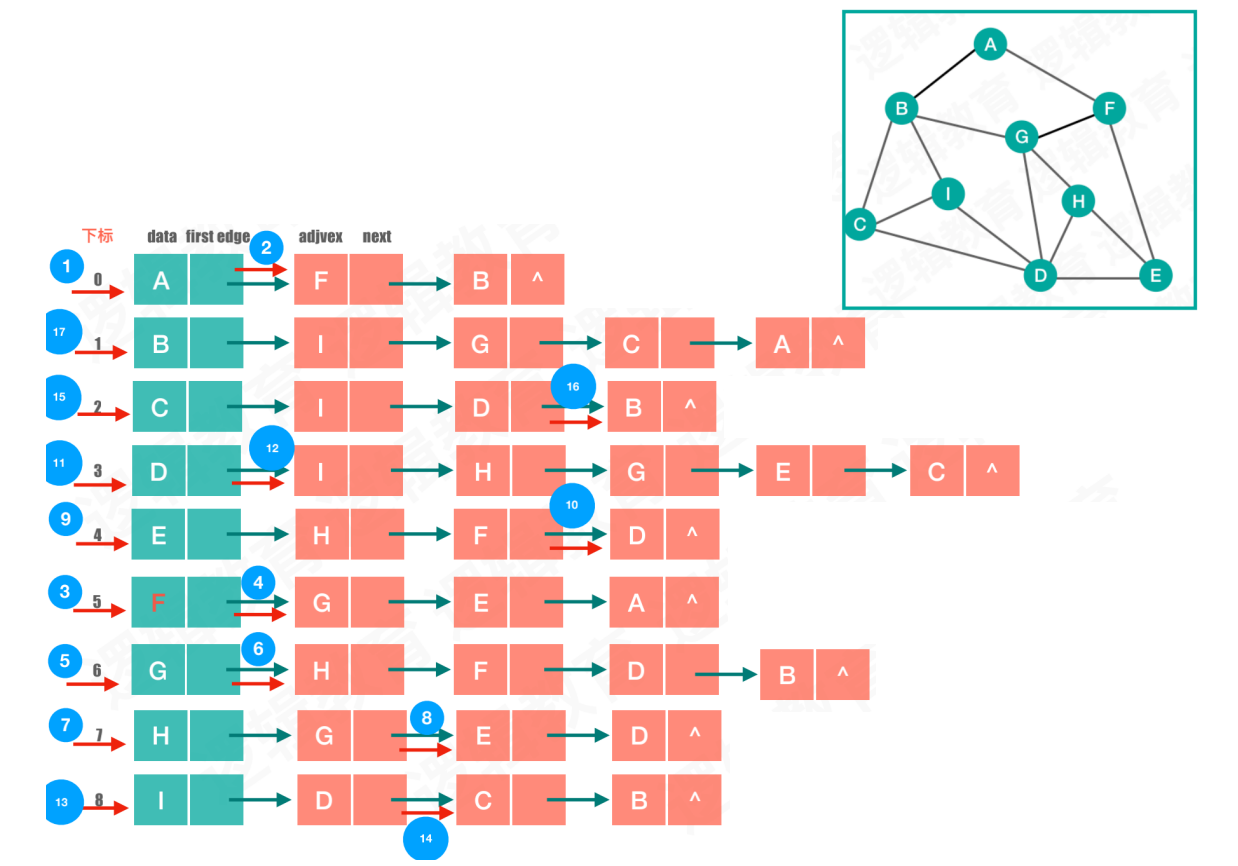
- 顶点依次的访问顺序:
A→F→G→H→E→D→I→C→B
延用上述“邻接表存储”的案例代码,在MGraphLinked类中增加以下代码:
class MGraphLinked {
var visited : [Int]?;
func DFSTraverse() -> String {
var str : String = "";
self.visited = [Int].init(repeating: 0, count: self.graph.node_num);
for i in 0 ..< self.graph.node_num {
if(self.visited![i] == 1){
continue;
}
DFS(str: &str, i: i);
}
return str;
}
fileprivate func DFS(str : inout String, i : Int){
self.visited![i] = 1;
let vNode = self.graph.adjList![i];
str += "\(vNode.data!),";
var node = vNode.firstEdge;
while(node != nil){
if(self.visited![node!.adj_vex_index!] == 1){
node = node?.next;
continue;
}
DFS(str: &str, i: node!.adj_vex_index!);
}
}
}
创建
visited数组,用来标记顶点是否已被访问根据顶点总数初始化
visited数组,默认未访问遍历顶点信息,如果该顶点未访问,调用
DFS方法进行深度优先遍历- 这一层循环的目的,为了解决非连通图中,未连接的顶点遍历
进入
DFS方法,将当前顶点标记为已访问,获取当前顶点所属链表的头结点将边表第一个结点赋值给
node,依次遍历所有node,为空停止当前
node索引值对应的顶点已被访问,将下一个邻接点赋值给node,并进入下一次循环否则,继续递归
DFS方法
创建邻接表,完成深度优先遍历:
let nodes = ["A", "B", "C", "D", "E", "F", "G", "H", "I"];
let arcs = [[0, 1], [0, 5],
[1, 2], [1, 6], [1, 8],
[2, 3], [2, 8],
[3, 4], [3, 6], [3, 7], [3, 8],
[4, 5], [4, 7],
[5, 6],
[6, 7]];
let isUndirected = true;
let graphLinked = MGraphLinked();
graphLinked.create(nodes: nodes, arcs: arcs, isUndirected: isUndirected);
print(graphLinked.traverse());
print("深度优先遍历:\(graphLinked.DFSTraverse())");
-------------------------
//输出以下内容:
A -> F,A -> B,
B -> I,B -> G,B -> C,B -> A,
C -> I,C -> D,C -> B,
D -> I,D -> H,D -> G,D -> E,D -> C,
E -> H,E -> F,E -> D,
F -> G,F -> E,F -> A,
G -> H,G -> F,G -> D,G -> B,
H -> G,H -> E,H -> D,
I -> D,I -> C,I -> B,
深度优先遍历:A,F,G,H,E,D,I,C,B,
3.2 广度优先遍历
广度优先遍历思想:从图中某顶点v出发,在访问了v之后依次访问v的各个未曾访问过的邻接点,然后分别从这些邻接点出发依次访问它们的邻接点,并使得“先被访问的顶点的邻接点先于后被访问的顶点的邻接点被访问,直至图中所有已被访问的顶点的邻接点都被访问到。如果此时图中尚有顶点未被访问,则需要另选一个未曾被访问过的顶点作为新的起始点,重复上述过程,直至图中所有顶点都被访问到为止
图的深度优先遍历和树的前序遍历相似,而图的广度优先遍历和树的层序遍历相似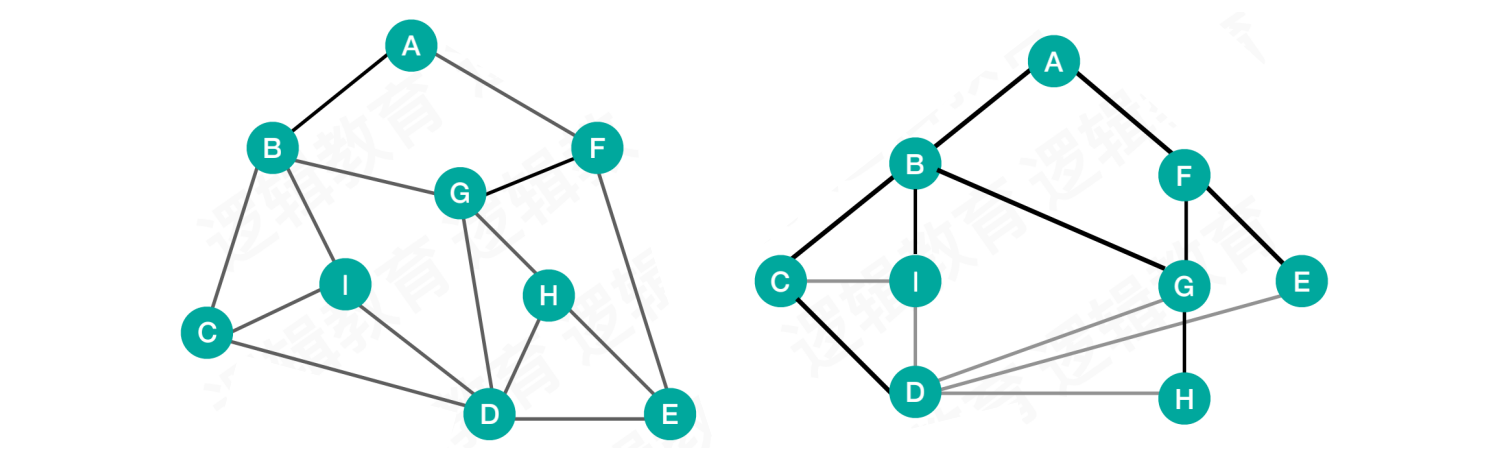
- 上面左右两图是完全一样的,只是右图排列的更像一棵树
3.2.1 特点
需要使用队列结构辅助完成
把根结点放到队列的末尾
每次从队列的头部取出⼀个元素,查看这个元素所有的下⼀级元素,把它们放到队
列的末尾。并把这个元素记为它下⼀级元素的前驱
找到所有元素后程序结束
如果遍历整棵树还没有找到,程序结束
示例: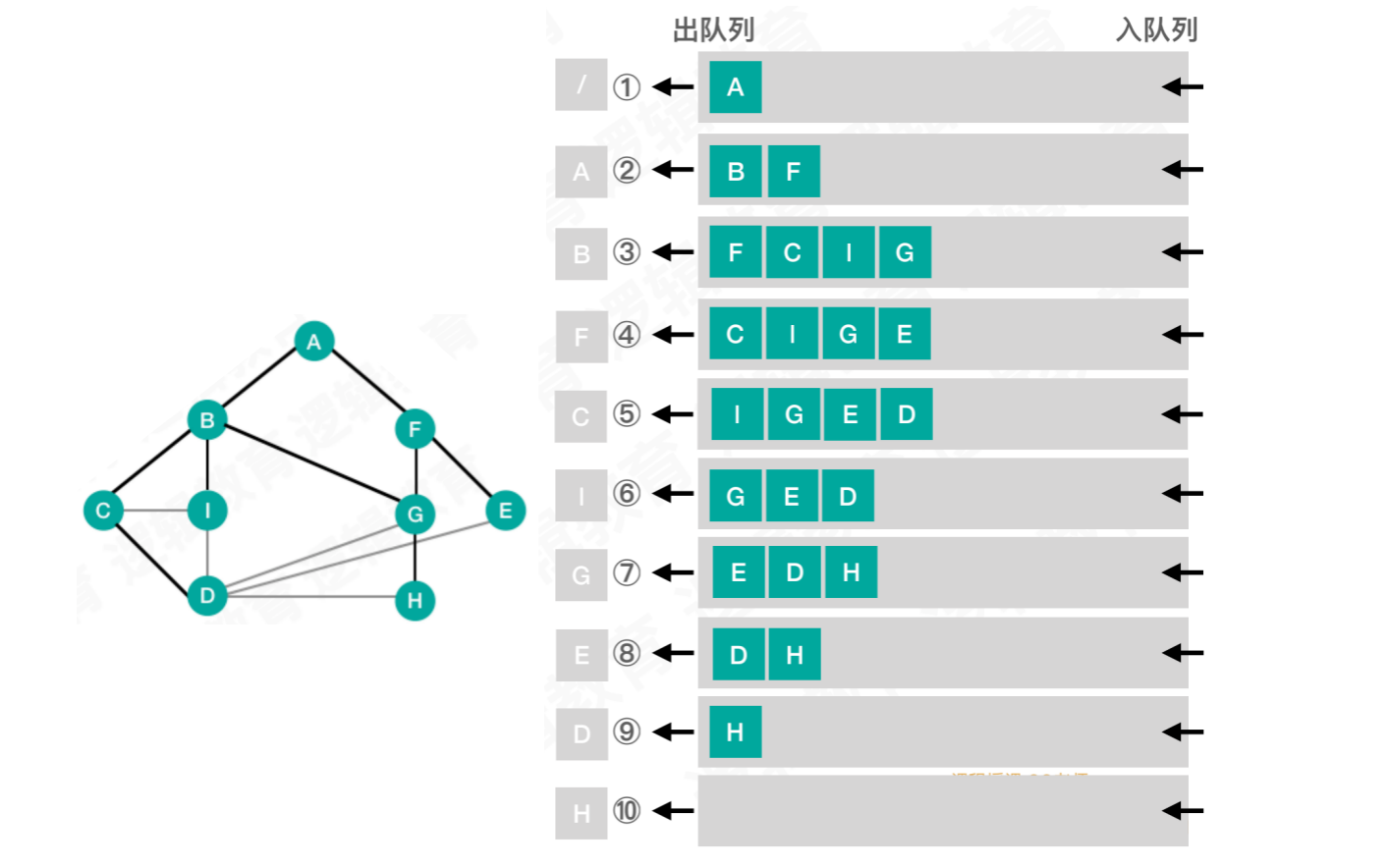
【步骤一】将
结点A入队【步骤二】将
结点A出队,并标记为已访问。然后将结点A的下一级元素,即邻接点B和F入队【步骤三】将
结点B出队并标记,结点B的邻接点有A、C、I、G。由于结点A已访问,将C、I、G入队【步骤四】将
结点F出队并标记,邻接点A、G、E。由于结点A已访问,结点G在队列中已存在,所以将结点E入队【步骤五】将
结点C出队,邻接点B、I、D,将结点D入队【步骤六】将
结点I出队,邻接点B、C、D。由于B、C已访问,结点D在队列中已存在,所以本次没有结点可入队【步骤七】将
结点G出队,邻接点B、F、E、H,将结点H入队【步骤八】将
结点E出队,邻接点F、D,没有结点可入队【步骤九】将
结点D出队,邻接点C、I、G、E、H,没有结点可入队【步骤十】将
结点H出队,邻接点D、G,没有结点可入队。此时找到所有元素,程序结束
3.2.2 邻接矩阵遍历
延用上述“邻接矩阵存储”的案例代码,在MGraphLinear类中增加以下代码:
class MGraphLinear {
var queue : LinkedQueue<Int>?;
func BFSTraverse() -> String {
var str : String = "";
self.queue = LinkedQueue<Int>();
self.visited = [Int].init(repeating: 0, count: self.graph.numNodes);
for i in 0 ..< self.graph.numNodes {
if(self.visited![i] == 1){
continue;
}
self.visited![i] = 1;
self.queue?.enter(element: i);
while(!self.queue!.isEmpty()){
let i = self.queue!.out()!
str += "\(self.graph.vexs![i]),";
for j in 0 ..< self.graph.numNodes {
if(self.graph.arc![i][j] == 0 || self.visited![j] == 1){
continue;
}
self.visited![j] = 1;
self.queue?.enter(element: j);
}
}
}
return str;
}
}
创建队列
创建
visited数组,用来标记顶点是否已被访问根据顶点总数初始化
visited数组,默认未访问遍历顶点信息,如果该顶点未访问,将其索引值加入队列,并标记已访问
- 这一层循环的目的,为了解决非连通图中,未连接的顶点遍历
进行队列的遍历,队列为空才会停止
进行出队操作,将出队索引赋值
i遍历顶点信息
如果边表中
[i][j]位置为0,表示两个顶点之间未连接,跳过循环如果该顶点已被访问,跳过循环
否则,将其索引值加入队列,标记已访问,并进入下一次循环
创建邻接矩阵,完成广度优先遍历:
let nodes = ["A", "B", "C", "D", "E", "F", "G", "H", "I"];
let edges = [[0, 1 ,1], [0, 5, 1],
[1, 2, 1], [1, 6, 1], [1, 8, 1],
[2, 3, 1], [2, 8, 1],
[3, 4, 1], [3, 6, 1], [3, 7, 1], [3, 8, 1],
[4, 5, 1], [4, 7, 1],
[5, 6, 1],
[6, 7, 1]];
let isUndirected = true;
let graphLinear = MGraphLinear();
graphLinear.create(nodes: nodes, edges: edges, isUndirected: isUndirected);
print(graphLinear.traverse());
print("广度优先遍历:\(graphLinear.BFSTraverse())");
-------------------------
//输出以下内容:
0 1 0 0 0 1 0 0 0
1 0 1 0 0 0 1 0 1
0 1 0 1 0 0 0 0 1
0 0 1 0 1 0 1 1 1
0 0 0 1 0 1 0 1 0
1 0 0 0 1 0 1 0 0
0 1 0 1 0 1 0 1 0
0 0 0 1 1 0 1 0 0
0 1 1 1 0 0 0 0 0
广度优先遍历:A,B,F,C,G,I,E,D,H,
3.2.3 邻接表遍历
延用上述“邻接表存储”的案例代码,在MGraphLinked类中增加以下代码:
class MGraphLinked {
var queue : LinkedQueue<Int>?;
func BFSTraverse() -> String {
var str : String = "";
self.queue = LinkedQueue<Int>();
self.visited = [Int].init(repeating: 0, count: self.graph.node_num);
for i in 0 ..< self.graph.node_num {
if(self.visited![i] == 1){
continue;
}
self.visited![i] = 1;
self.queue?.enter(element: i);
while(!self.queue!.isEmpty()){
let i = self.queue!.out()!
let vNode = self.graph.adjList![i];
str += "\(vNode.data!),";
var node = vNode.firstEdge;
while(node != nil){
if(self.visited![node!.adj_vex_index!] == 0){
self.visited![node!.adj_vex_index!] = 1;
self.queue?.enter(element: node!.adj_vex_index!);
}
node = node?.next;
}
}
}
return str;
}
}
创建队列
创建
visited数组,用来标记顶点是否已被访问根据顶点总数初始化
visited数组,默认未访问遍历顶点信息,如果该顶点未访问,将其索引值加入队列,并标记已访问
- 这一层循环的目的,为了解决非连通图中,未连接的顶点遍历
进行队列的遍历,队列为空才会停止
进行出队操作,将出队索引赋值
i,获取当前顶点所属链表的头结点将边表第一个结点赋值给
node,依次遍历所有node,为空停止当前
node索引值对应的顶点未访问,将其索引值加入队列,并标记已访问将下一个邻接点赋值给
node,并进入下一次循环
创建邻接表,完成广度优先遍历:
let nodes = ["A", "B", "C", "D", "E", "F", "G", "H", "I"];
let arcs = [[0, 1], [0, 5],
[1, 2], [1, 6], [1, 8],
[2, 3], [2, 8],
[3, 4], [3, 6], [3, 7], [3, 8],
[4, 5], [4, 7],
[5, 6],
[6, 7]];
let isUndirected = true;
let graphLinked = MGraphLinked();
graphLinked.create(nodes: nodes, arcs: arcs, isUndirected: isUndirected);
print(graphLinked.traverse());
print("广度优先遍历:\(graphLinked.BFSTraverse())");
-------------------------
//输出以下内容:
A -> F,A -> B,
B -> I,B -> G,B -> C,B -> A,
C -> I,C -> D,C -> B,
D -> I,D -> H,D -> G,D -> E,D -> C,
E -> H,E -> F,E -> D,
F -> G,F -> E,F -> A,
G -> H,G -> F,G -> D,G -> B,
H -> G,H -> E,H -> D,
I -> D,I -> C,I -> B,
广度优先遍历:A,F,B,G,E,I,C,H,D,
总结
图的初识:
图(
Graph) 是由顶点的有穷⾮空集合和顶点之间边的集合组成,图结构中的结点称之为顶点顶点之间关系是任意的
图结构中,不允许没有顶点,也不存在空图一说
图中的任意点都可作为起点,即使两点不相邻,它们之间也可能存在关系
通常表示为
G(V, E)G表示⼀个图V是图G中的顶点集合E是图G中边的集合
图的定义:
无向图 & 无向边:顶点之间连接的边没有方向,称之为无向边。由这些无向边连接的图,称之为无向图
有向图 & 有向边:顶点之间连接的边有箭头指向,称之为有向边。由这些有向边连接的图,称之为有向图
无向完全图:某一个点到任意点都被无向边直接连接,称之为无向完全图
有向完全图:某一个点到任意点都被有向边直接连接,并且顶点与顶点之间被双向箭头连接,称之为有向完全图
网:顶点与顶点连接带有权值的图,称之为网
子图:从一个图中可以拆分出很多子图
环:从第一个顶点到最后一个顶点之间是闭合的
连通图:图中顶点之间相互都是连通的,称之为连通图
非连通图:图中存在无法连通的顶点,该图属于非连通图
图的存储:
图的两个特点,顶点和边。我们通过顶点和边的连接,可以确定图的逻辑关系。所以图的存储,需要考虑顶点的存储,以及边与边的连接信息
所谓“边”,就是两点之间连接的线。在无向图中称之为“边”,在有向图中称之为“弧”
图的邻接矩阵存储:
邻接矩阵存储,本质上就是采用顺序存储,将图的逻辑进行存储
采用顺序存储,将顶点和边一起存储会相对困难,因为它们存在多对对的关系。所以我们可以将顶点和边分开存储
顶点可以直接使用一维数组存储
而连接关系,使用二维数组,和顶点分开存储
假设图中有
n个顶点,则邻接矩阵是⼀个n * n的⽅阵若两点之间有连接,表示为
1,否则为0对角线的位置一定为
0如果是无向图,横向和纵向存储的数据是对称的
顶点的度,是指邻接矩阵第
i行,或第j列,非0元素的总和如果是网,顶点直接到达另一个顶点,该位置填充权值。对角线位置为
0。没有连接关系的位置为∞,代码中可以使用Int.max表示使用邻接矩阵存储图,最大的弊端就是空间浪费
图的邻接表存储:
使用邻接表存储,本质上就是采用链式存储,它可以避免空间浪费的问题
使用一维数组存储所有顶点,数组中的每一个顶点结点,都可以连接它的边表结点,从而形成一条链表
顶点元素的数据结构,存在数据域和指针域。数据域存储顶点信息,指针域指向边表中的第一个结点,相当于链表中的头结点
边表结点的数据结构,存在邻接点域和指针域。邻接点域存储邻接点信息,指针域指向和顶点有关系的下一个邻接点
由于图中顶点之间是无序的,所以顶点和邻接点的连接也没有固定的顺序
获取一个顶点的度,就是它所对应的链表长度
判断
vi和vj是否存在连接关系,需要进行链表的遍历如果是有向图,顶点和邻接点的连接关系仅取决于箭头方向。将箭头方向相反的顶点进行连接,就会形成逆邻接表
如果是网,我们要在边表结点的数据结构中,增加权值的存储
图的遍历:
图的遍历是指:从给定图中任意指定的顶点(称为初始点)出发,按照某种搜索方法沿着图的边访问图中的所有顶点,使每个顶点仅被访问一次
图的遍历,科学遍历方法可以划分为以下两种策略:
深度优先遍历(
DFS,Depth First Search)广度优先遍历(
BFS,Breadth First Search)
图的深度优先遍历:
- 深度优先遍历的思想:假设初始状态是图中所有顶点均未被访问,则从某个顶点v出发,首先访问该顶点,然后依次从它的各个未被访问的邻接点出发深度优先搜索遍历图,直至图中所有和v有路径相通的顶点都被访问到。若此时尚有其他顶点未被访问到,则另选一个未被访问的顶点作起始点,重复上述过程,直至图中所有顶点都被访问到为止
图的深度优先遍历:
广度优先遍历思想:从图中某顶点v出发,在访问了v之后依次访问v的各个未曾访问过的邻接点,然后分别从这些邻接点出发依次访问它们的邻接点,并使得“先被访问的顶点的邻接点先于后被访问的顶点的邻接点被访问,直至图中所有已被访问的顶点的邻接点都被访问到。如果此时图中尚有顶点未被访问,则需要另选一个未曾被访问过的顶点作为新的起始点,重复上述过程,直至图中所有顶点都被访问到为止
广度优先遍历,需要使用队列结构辅助完成

