问题描述

extrude中文译作挤压，sweep译作扫掠。前者为将一个shape沿着向量延申，生成一个3D图形。后者为为对一个shape沿着路径延申，生成一个3D图形。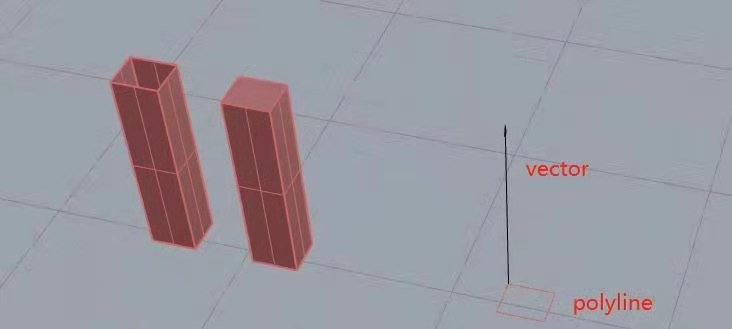

extrude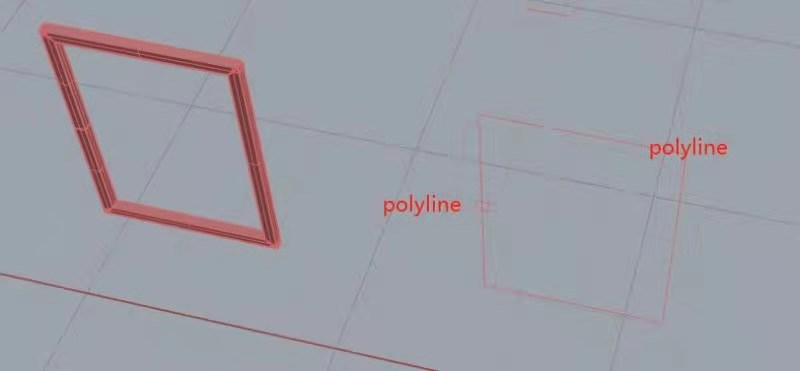

sweep

代码背景

由于是前端开发，我们选择的是前端3D开发代码库three.js，该代码库提供了很多3D开发接口，后面的代码实现介绍中会有体现。
不难发现，在three.js中的geometry中本身就有ExtrudeGeometry这个类，但是这个已经给出的类没有办法实现我们的需求，缺陷有以下几个：

它的输入为shape和一个配置项，首先在three.js中，shape是一个2D图形，它可以有很多种生成方式，但是必须都是2D的点。我们给定的输入是一组三维空间上的坐标数组，无法生成一个所谓的shape。

以下是我们的一组示例给定输入：

 "shape": {
      "type": "Polygon",
      "coordinates": [
        [
          [0.004999999999999987, 8.971000000000002, 0.33],
          [0.012029437251522845, 8.98797056274848, 0.33],
          [0.028999999999999988, 8.995000000000001, 0.33],
          [0.13, 8.995000000000001, 0.33],
          [0.231, 8.995000000000001, 0.33],
          [0.2479705627484772, 8.98797056274848, 0.33],
          [0.255, 8.971000000000002, 0.33],
          [0.2549999999999999, 8.82, 0.33],
          [0.25499999999999984, 8.669, 0.33],
          [0.24797056274847695, 8.652029437251523, 0.33],
          [0.23099999999999982, 8.645000000000001, 0.33],
          [0.1299999999999998, 8.645000000000001, 0.33],
          [0.028999999999999866, 8.645000000000001, 0.33],
          [0.012029437251522876, 8.652029437251523, 0.33],
          [0.004999999999999859, 8.669, 0.33],
          [0.004999999999999923, 8.82, 0.33],
          [0.004999999999999987, 8.971000000000002, 0.33]
        ]
      ]
    },
    "path": {
      "type": "LineString",
      "coordinates": [
        [0, 0, 0],
        [0, 0, 2.715]
      ]
    }
}

它生成的3D图形的shape切面必须和给定的路径的切向量空间垂直

// 给定的shape
const shape = new THREE.Shape([
new THREE.Vector2(0, 0),
new THREE.Vector2(1, 0),
new THREE.Vector2(1, 1),
new THREE.Vector2(0, 1),
]);
// 给定的向量
const line = new THREE.LineCurve3(
new THREE.Vector3(10, 0, 0),
new THREE.Vector3(10, 10, 10)
);

原先 (右边为挪移后的向量，用来进行路径对比，后同)

改进

可以观察出原先的实现中给定的shape会通过翻转使得其初始位置和给定的向量垂直，而不是我们想要的shape沿向量扩展成的3D图形。

sweep的转向
sweep的转角

原先

改进

转向，即需要计算方向转换后的shape方向的旋转。比如上图后转角后shape的方向也需要变化。
sweep的转角的处理，要生成的如框体这类geometry是需要这样的sweep操作，因此对于转角需要做相应的处理。

至此，要实现我们需要的extrude和sweep操作，不考虑代码优化，从算法层面，这三个问题必须要解决，后面我们将会以这些问题作为主要线索来说明算法实现。

具体实现

shape转化

 "shape": {
      "type": "Polygon",
      "coordinates": [
        [
          [0.004999999999999987, 8.971000000000002, 0.33],
          [0.012029437251522845, 8.98797056274848, 0.33],
          [0.028999999999999988, 8.995000000000001, 0.33],
          [0.13, 8.995000000000001, 0.33],
          [0.231, 8.995000000000001, 0.33],
          [0.2479705627484772, 8.98797056274848, 0.33],
          [0.255, 8.971000000000002, 0.33],
          [0.2549999999999999, 8.82, 0.33],
          [0.25499999999999984, 8.669, 0.33],
          [0.24797056274847695, 8.652029437251523, 0.33],
          [0.23099999999999982, 8.645000000000001, 0.33],
          [0.1299999999999998, 8.645000000000001, 0.33],
          [0.028999999999999866, 8.645000000000001, 0.33],
          [0.012029437251522876, 8.652029437251523, 0.33],
          [0.004999999999999859, 8.669, 0.33],
          [0.004999999999999923, 8.82, 0.33],
          [0.004999999999999987, 8.971000000000002, 0.33]
        ]
      ]
    },
    "path": {
      "type": "LineString",
      "coordinates": [
        [0, 0, 0],
        [0, 0, 2.715]
      ]
    }
}

正如前述的问题，我们拿到了shape三维点数组，无论是从简化代码还是从复用原先代码的角度上，将这个三维数组转化成一组二维点数组都是非常有道理的，而之后也可以看到这样简化之后代码在实现上很多地方都会变方便。
在说明代码之前，首先我们需要规范下给定输入的类型，即：

export type shapeArrType = {
  // 外轮廓（唯一）
  outerArr: Array<[number, number, number]>;
  // 内轮廓（空洞 数组）
  innerArr: Array<Array<[number, number, number]>>;
};
// 路径
pathArr: [number, number, number][];

接着我们需要分析一下该操作的可行性。通过调研得知，给定的shape虽然是一组三维点坐标，但是它们是确定在一个平面上的，基于这一原因，将一个三维坐标阵转化为二维坐标阵是可行的，实际上我们要做两个操作。第一个操作是将shape所在的平面进行rotation操作，使其和xOy平面平行；第二个操作是将平行的平面在z轴方向做translation操作，使其成为xOy平面。此时，我们取所有平面上的点（转化后的）x、y坐标作为我们转化后shape的二维坐标。
这时，当给定的shape被rotation和translation，我们给定的向量也应当受到同样的rotation作用，但是由于是向量，只应该受到rotation作用而不会受到translation作用。
同时，思考一点，即向量的初始位置。由于是向量，从数学角度来说，并没有初始位置这一概念，只有方向和大小两个指标。但是在数据的表现中，向量是以路径的形式表现的，因此我们需要对向量做一个translation使其初始坐标变为(0, 0, 0)，否则在向量的作用计算中会产生很大rotation偏移量。这里有点抽象，所以举一个例子。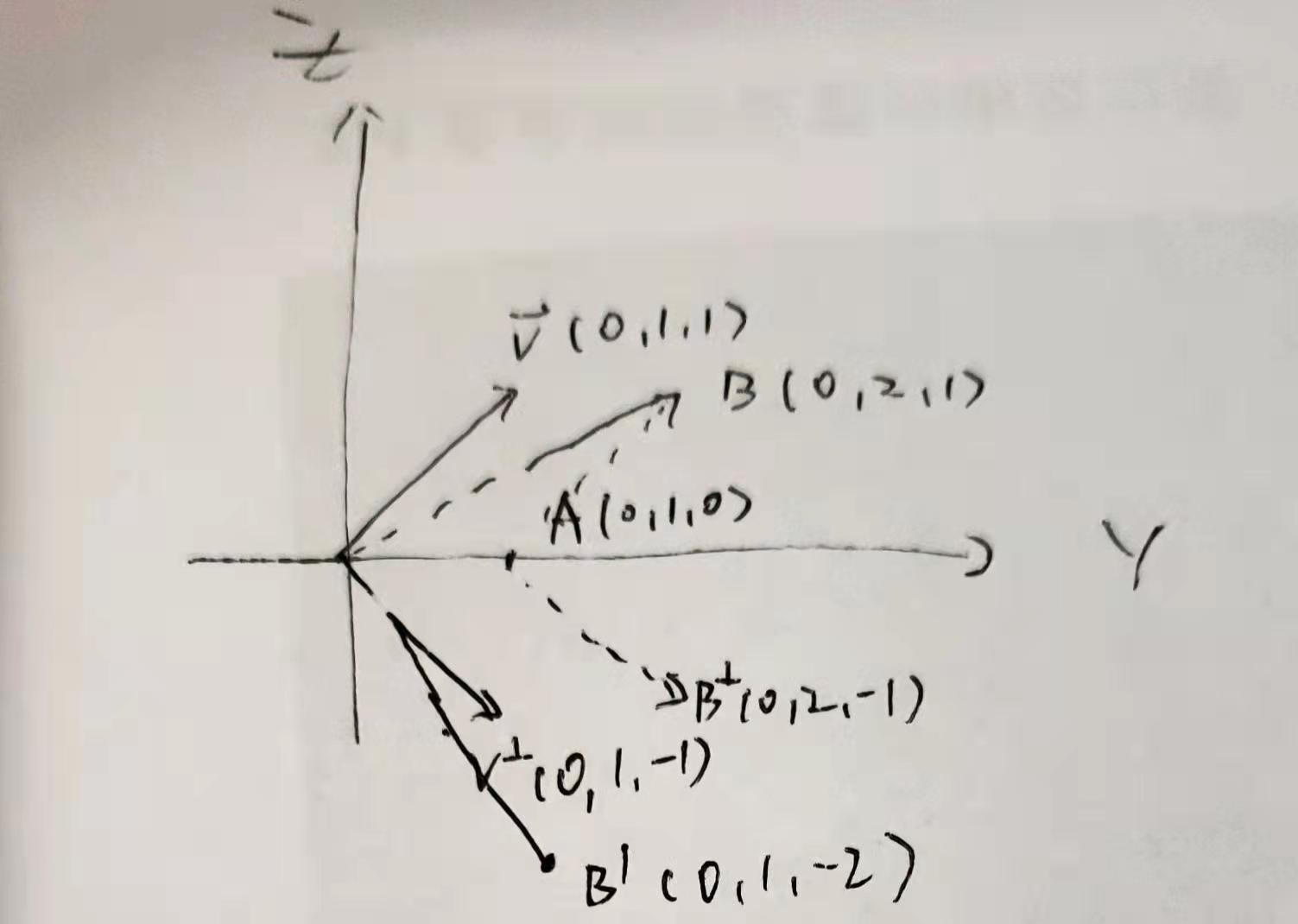

只考虑yOz平面，给定向量translationv(0,1,1)和点 A(0,1,0)，然后设定rotation为顺时针90。。如果先作用translation再作用translation会得B、(0,1,-2)，但是我们需要的是先做rotation再做translation，得到
B⊥(0,2,-1)，这样的差异会在实际的使用被更大的放大。其实从矩阵的角度会更好理解，因为这样的作用实际上都是矩阵作用，而矩阵作用是不满足交换律的，因此我们需要提前将向量放在(0, 0, 0)上，避免出现旋转的偏差。
同时这个向量translation实际上从空间角度是作用在整个geometry上的，所以实际上对所有给定的点坐标都会有这样的一个translation作用。
综上，我们会有三个变换，分别是向量起始点的translation变化，shape通过变换回到xOy平面的变换，向量根据shape的变化进行的相应的旋转变换，这三个变换在代码中以Matrix4类型刻画，对的变量为：

// 根据向量起始点进行的所有点的变换
const mVec = new Matrix4();
// 创建基的转化矩阵(只包含旋转) 目的是让法向量为(0,0,1)可以转换为2D平面
// 对于向量 只用旋转 不能位移
// 前者用于变化向量 后者用于变化点
const mRot = new Matrix4();
const mGen = new Matrix4();

正如上面所说，对于向量起始点的geometry的translation变换为初始步骤，对应实现为局部函数paramSet，

const paramSet = () => {
  if (!options.pathArr?.length || options.pathArr.length === 0) {
    throw new Error('无路径点');
  }
  const startPoint = new Vector3(options.pathArr[0][0], options.pathArr[0][1], options.pathArr[0][2]);
  mVec.setPosition(startPoint).invert();
  const numberArrTransform = (arr: [number, number, number]): [number, number, number] => {
    return [arr[0] - startPoint.x, arr[1] - startPoint.y, arr[2] - startPoint.z];
  };
  shapeArr.outerArr = shapeArr.outerArr.map(numberArrTransform);
  shapeArr.innerArr.forEach((holeArr, index) => {
    shapeArr.innerArr[index] = holeArr.map(numberArrTransform);
  });
  options.pathArr = options.pathArr.map(numberArrTransform);
};

下一步，计算shape的旋转矩阵，

const getTransformMatrix = () => {
      // 找到平面上的三个点 A, B, C
      const vertA = outerArr[0];
      const vertB = outerArr[1];
      let cIndex = 2;
      let vertC!: [number, number, number];
      let vecAB!: Vector3;
      let vecAC!: Vector3;
      // 获取不在一条支线上的点C
      const getVectors = () => {
        vertC = outerArr[cIndex];
        // 找到向量 AB AC
        vecAB = new Vector3(vertB[0] - vertA[0], vertB[1] - vertA[1], vertB[2] - vertA[2]);
        vecAC = new Vector3(vertC[0] - vertA[0], vertC[1] - vertA[1], vertC[2] - vertA[2]);
        const vectorCross = new Vector3();
        vectorCross.crossVectors(vecAB, vecAC);
        // 此时选择了三个在一条直线上的点
        if (isEqual(vectorCross.lengthSq(), 0)) {
          cIndex++;
          if (cIndex >= outerArr.length) {
            throw new Error('所有点都是平行点');
          }
          getVectors();
        }
      };
      getVectors();
      // 计算平面法向量
      const normal = new Vector3();
      normal.crossVectors(vecAB, vecAC);
      // 法向量作为新坐标系的基向量z方向
      const zb = normal.normalize();
      // AB作为基的x方向
      const xb = vecAB.normalize();
      // 根据两个基算出第三个基
      const yb = new Vector3();
      yb.crossVectors(zb, xb);
      yb.normalize();
      // 创建基的转化矩阵(只包含旋转) 目的是让法向量为(0,0,1)可以转换为2D平面
      // 对于向量 只用旋转 不能位移
      const mRot = new Matrix4();
      mRot.makeBasis(xb, yb, zb);
      mRot.invert();
      // 测试用 实际只用vA
      const vA = new Vector3(vertA[0], vertA[1], vertA[2]);
      const vB = new Vector3(vertB[0], vertB[1], vertB[2]);
      const vC = new Vector3(vertC[0], vertC[1], vertC[2]);
      vA.applyMatrix4(mRot);
      vB.applyMatrix4(mRot);
      vC.applyMatrix4(mRot);
      // 生成位移矩阵 目的是将平面的zIndex变为0
      const zConstant = vA.z;
      const mTrans = new Matrix4();
      mTrans.makeTranslation(0, 0, -zConstant);
      const mGen = mTrans.clone();
      mGen.multiply(mRot);
      // 前者用于变化向量 后者用于变化点
      return {
        mRot: mRot,
        mGen: mGen
      };
    };

上面的函数实际上在做这样的事情，首先需要进行平面的刻画，根据立体几何知识，刻画一个3D平面需要找到该平面上不共线的三个点，12行的getVectors做的就是这样一件事。在得到这样的三个点后，首先计算shape的rotation对应的Matrix4。
要计算rotation的矩阵，我们可以通过计算给定平面和xOy平面在x、y、z轴上的旋转角度，但是这样做很麻烦。我们不妨转换下思维，即如果把xOy平面变成给定shape的所在平面，我们只需要将坐标系进行变基操作即可，本质上这和求出旋转角度进而计算是相同的。而计算我们给定shape平面的基向量是个很简单的事情，所以就很方便。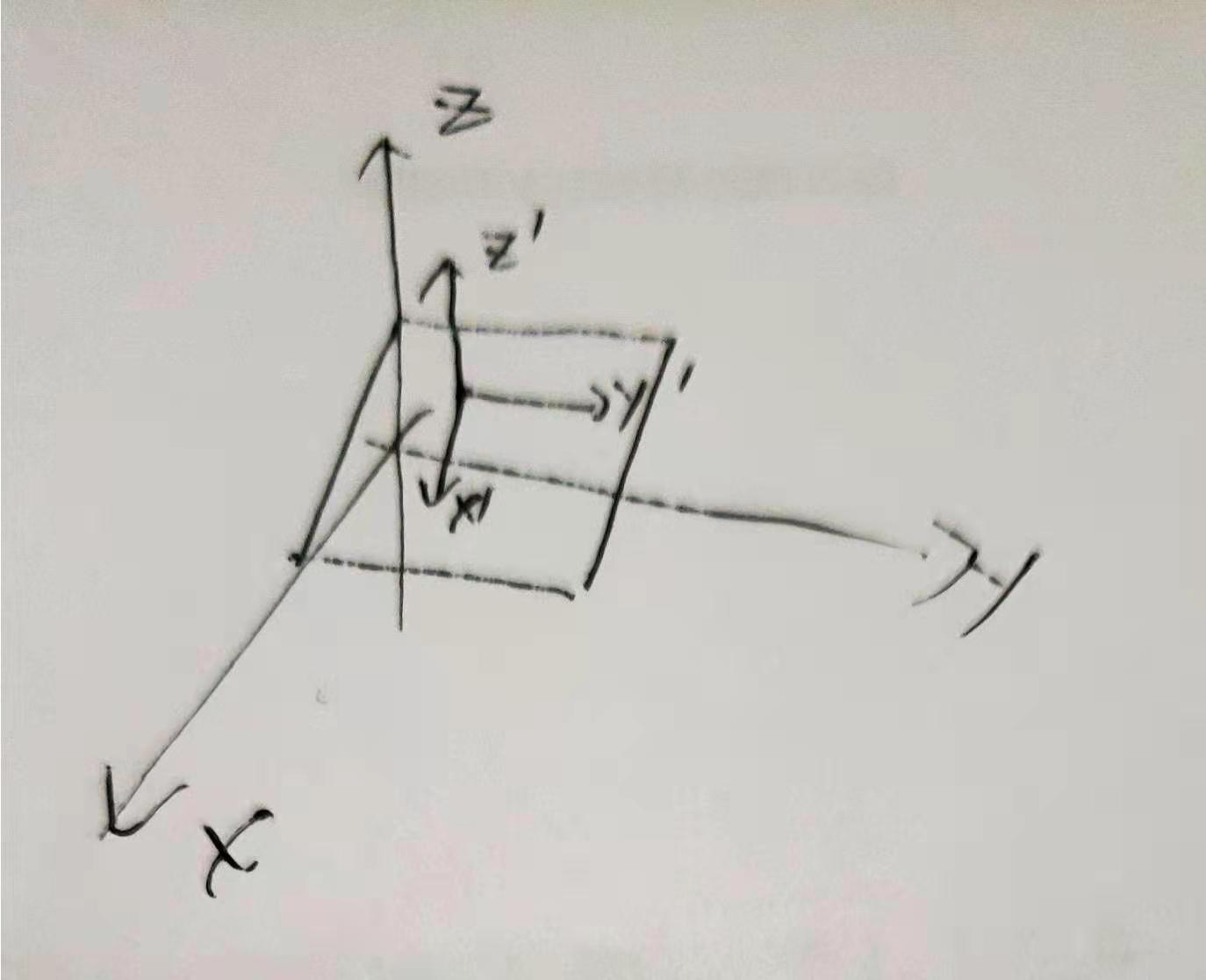

现在说明下如何根据三个点去求平面的基向量，32-47行代码，我们取三个点分别为A, B, C，然后求法向量，即ABxAC，该方向即平面法向量方向，单位化该向量即得到基向量的z向量。取向量AB的单位化向量作为x方向基向量，可以用z方向基向量和x方向基量的叉积可以得到y方向的基向量。
用得到基向量填充矩阵，即可以得到从默认基向量到shape对应的基向量的Matrix4，即xOy平面到shape平面的rotation矩阵，取该矩阵的反得到将shape平面旋转为和xOy平面平行的rotation矩阵。
将rotation矩阵作用域点A，得到的新的点的z方向坐标即translation矩阵的偏移量。简单处理后，可以返回两个Matrix4。

// 转化所有点为二维向量
const transformInput = () => {
  // 3D坐标转化为2D坐标
  const transformPoint3DTo2D = (vertex: [number, number, number]) => {
    const v = new Vector3(vertex[0], vertex[1], vertex[2]);
    v.applyMatrix4(mGen);
    if (!isEqual(v.z, 0)) {
      throw 'not plate';
    }
    // 转化为2D坐标
    const ret = new Vector2(v.x, v.y);
    return ret;
  };
  const outerArr2Ds = outerArr.map(transformPoint3DTo2D);
  const innerHoleArr = innerArr.map(holes => {
    // 每一个holes中的点进行转化
    return holes.map(transformPoint3DTo2D);
  });
  return {
    outerArr2Ds,
    innerHoleArr
  };
};

计算出mGen后，将所有点做变换，得到的点就是shape在xOy平面上的对应点（z值都是0），取其x, y值，可以得到对应的二维方向坐标。
到这一步结束后，我们将原来的问题转化为一个2Dshape在空间上的相应的extrude和sweep。这样得到的geometry需要在生成结束后进行逆变换，即：

// 还原
mGen.invert();
mVec.invert();
this.applyMatrix4(mGen);
this.applyMatrix4(mVec);

此时，在空间上得到的geometry即给定参数对应的geometry。

路径分点

在阐述接下来的代码实现前，先说明下具体的思路，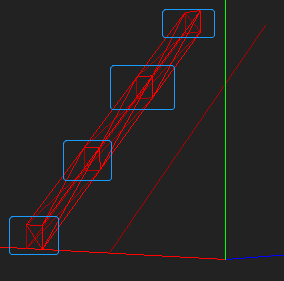

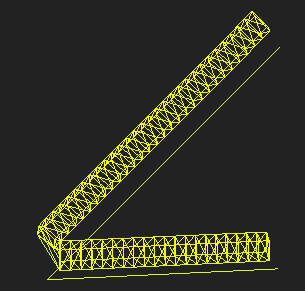
观察图中的由xOy平面上的shape通过extrude操作得到的geometry，它是由多个基础面连接而成的，因此要实现extrude操作的第一步是绘制这些平面，或者说计算这些平面的点的位置。可以看到图中的蓝框位置，即给定平面在路径上平移后的点的位置，要确定这些点的位置需要两个参数，第一是shape中绘图点的位置，如图中是正方形的4个点，第二是路径上点的位置。比如实例中，我们选择了直线上的三个点（设置参数step=3），可以看到对应的图形出现在向量的对应的三等分点位置。实际计算中，路径可能是曲线，或者有多段路径，因此路径中取点的计算是接下来的重要环节。

// 输入参数 steps 标识拉伸线条中细分线段的点数 默认为1
const getSpacedPointsExtend = (path: CurvePath<Vector3>, divisions = 40) => {
  // 总长度
  const allLength = path.getLength();
  // 有几条曲线 用于生成端点
  const curveLengths = path.getCurveLengths();
  const pointRate: number[] = [];
  const cornerRateList: number[] = [];
  if ((path as any).autoClose) {
    isClosed = true;
  }
  curveLengths.forEach((curveLength, index) => {
    // 最后一条曲线（存储一点作为最后的连接点）
    if (index === curveLengths.length - 1) {
      return;
    }
    // 计算当前分curve的末端位置
    const rate = curveLength / allLength;
    // 前者对应前曲线末端 后者对应后曲线开端
    pointRate.push(rate - 1 / (100 * divisions));
    pointRate.push(rate);
    pointRate.push(rate + 1 / (100 * divisions));
    // 用于查找rate的index列表
    cornerRateList.push(rate);
  });
  // 多余的图形 分别为拐角的前后两个面 以及拐角的对应面
  const newDivision = divisions - pointRate.length - (isClosed ? 2 : 0);
  if (newDivision <= 0) {
    throw '当前参数的step太小，不足以生成';
  }
  for (let i = 0; i <= newDivision; i++) {
    pointRate.push(i / newDivision);
  }
  // 将所有点进行排序
  pointRate.sort((a, b) => a - b);
  // 找到所有corner点对应的数值
  cornerIndexList = cornerRateList.map(rate => {
    return pointRate.findIndex(pr => pr === rate);
  });
  if (isClosed) {
    pointRate.push(1);
    pointRate.push(0.01);
    cornerIndexList.push(pointRate.length - 2);
  }
  rateList = pointRate;
  // 获取对应点
  const points: Vector3[] = pointRate.map(rate => path.getPoint(rate));
  return points;
};

此处这里用到three.js中Path类的getPoint方法，该方法输入[0, 1]的一个数字（曲线上的对应点在整条曲线上的位置）返回曲线在该位置上的点的向量。
我们在实现中需要特殊处理一下获取点的rate，因为需要考虑sweep在线与线的转角间的绘制，如果转角的点附近没有shape绘制，最后的图形就会很失真，因此取点时需要取到前一条曲线的最后一个点和下一条曲线的开始点，参考13-26行。
特别的，如果要求绘制的geometry是封闭的，代码中需要为geometry设置封闭点，即需要将最后的点取到开始点，即43-47行做的事情。

// 确定路径上的分割点的位置 但是拐弯的地方和预想并不相同
extrudePts = getSpacedPointsExtend(extrudePath as any, steps);
// 路径向量点 只反转方向 没有位移
extrudePts.forEach(vertex => vertex.applyMatrix4(mRot));

获取路径分点后，需要进行rotation变换，原因见前面叙述。注意，第4行代码，我们只是把路径中的点对应位置算出来了，但是路径是没有经过mRot作用的（没有提供该方法，所以后面考虑路径相关问题时，仍需要考虑mRot的作用）。

Frenet坐标系计算

在说明前，先介绍下Frenet标架，大家可以参考下文档或知乎上的简介。简而言之可以理解为Frenet标架是一个可以描述曲线运动的一种方式。它和直角坐标系描述曲线上点的坐标轨迹不同，它是通过去研究曲线的弧长（这是一个绝对对于曲线有意义的标量），进而研究曲线的运动方向的一种描述方式。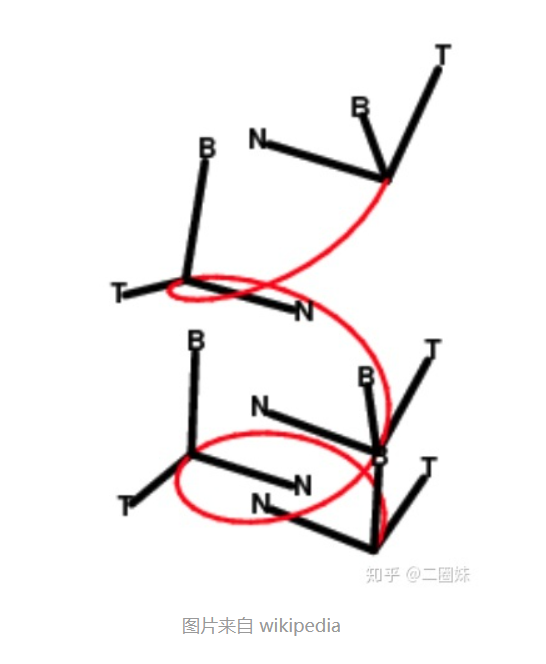

它的维度体现在曲线运动的切线方向T，法线方向N和副法线方向B这三个向量。考虑二维圆周运动，不难发现在每个运动位置点都有切向变化和法向变化（向心），扩展到三维空间，增加了一个副法向，描述在上下方向上的变化。具体有兴趣可以去看文档研究下，这里就说这么多。

const computeFrenetFramesExtend = (segmentRates: number[], path: CurvePath<Vector3>, closed = false) => {
  // see http://www.cs.indiana.edu/pub/techreports/TR425.pdf
  const normal = new Vector3();
  const segments = segmentRates.length;
  const tangents: Vector3[] = [];
  const normals: Vector3[] = [];
  const binormals: Vector3[] = [];
  const vec = new Vector3();
  const mat = new Matrix4();
  // compute the tangent vectors for each segment on the curve
  segmentRates.forEach((rate, index) => {
    tangents[index] = path.getTangentAt(rate, new Vector3());
    // 正规化
    tangents[index].normalize();
  });
  // select an initial normal vector perpendicular to the first tangent vector,
  // and in the direction of the minimum tangent xyz component
  normals[0] = new Vector3();
  binormals[0] = new Vector3();
  let min = Number.MAX_VALUE;
  const tx = Math.abs(tangents[0].x);
  const ty = Math.abs(tangents[0].y);
  const tz = Math.abs(tangents[0].z);
  if (tx <= min) {
    min = tx;
    normal.set(1, 0, 0);
  }
  if (ty <= min) {
    min = ty;
    normal.set(0, 1, 0);
  }
  if (tz <= min) {
    normal.set(0, 0, 1);
  }
  vec.crossVectors(tangents[0], normal).normalize();
  normals[0].crossVectors(tangents[0], vec);
  binormals[0].crossVectors(tangents[0], normals[0]);
  // compute the slowly-varying normal and binormal vectors for each segment on the curve
  // 计算法向量和副法向量 该算法依赖于曲率中的基向量关系
  for (let i = 1; i < segments; i++) {
    normals[i] = normals[i - 1].clone();
    binormals[i] = binormals[i - 1].clone();
    vec.crossVectors(tangents[i - 1], tangents[i]);
    if (vec.length() > Number.EPSILON) {
      vec.normalize();
      const theta = Math.acos(clamp(tangents[i - 1].dot(tangents[i]), -1, 1)); // clamp for floating pt errors
      normals[i].applyMatrix4(mat.makeRotationAxis(vec, theta));
    }
    binormals[i].crossVectors(tangents[i], normals[i]);
  }
  // if the curve is closed, postprocess the vectors so the first and last normal vectors are the same
  if (closed === true) {
    let theta = Math.acos(clamp(normals[0].dot(normals[segments]), -1, 1));
    theta /= segments;
    if (tangents[0].dot(vec.crossVectors(normals[0], normals[segments])) > 0) {
      theta = -theta;
    }
    for (let i = 1; i < segments; i++) {
      // twist a little...
      normals[i].applyMatrix4(mat.makeRotationAxis(tangents[i], theta * i));
      binormals[i].crossVectors(tangents[i], normals[i]);
    }
  }
  // 切线 法向量 副法向量
  return {
    tangents: tangents,
    normals: normals,
    binormals: binormals
  };
};

这里的代码实现原理，可以参考文档去进行详细研究。但是作为工具化函数，只需要知道它返回曲线上给定的rate位置的切线方向T，法线方向N和副法线方向B这三个单位向量即可。

构建基平面

const shapePoints = shape.extractPoints(curveSegments);
let vertices = shapePoints.shape;
const holes = shapePoints.holes;
const reverse = !ShapeUtils.isClockWise(vertices);
// 如果面积为负 反转所有点 和洞的所有点
if (reverse) {
  vertices = vertices.reverse();
  // Maybe we should also check if holes are in the opposite direction, just to be safe ...
  for (let h = 0, hl = holes.length; h < hl; h++) {
    const ahole = holes[h];
    if (ShapeUtils.isClockWise(ahole)) {
      holes[h] = ahole.reverse();
    }
  }
}
// 生成给定shape的faces
const faces = ShapeUtils.triangulateShape(vertices, holes);

这一部分都是调用的Shape类的相关方法，根据给定的shape的2维转换点，计算出输入的对应shape的绘画点。

侧面计算

for (let i = 0; i < vlen; i++) {
    const vert = bevelEnabled ? scalePt2(vertices[i], verticesMovements[i], bs) : vertices[i];
  if (!extrudeByPath) {
    v(vert.x, vert.y, 0);
  } else {
    const vertice3D = new Vector3(vert.x, vert.y, 0);
    position2.copy(vertice3D).add(extrudePts[0]);
    v(position2.x, position2.y, position2.z);
  }
}
for (let s = 1; s <= steps; s++) {
  for (let i = 0; i < vlen; i++) {
    // bevelEnabled现在只考虑false情况，即对应的shape的相对绘制点
    const vert = bevelEnabled ? scalePt2(vertices[i], verticesMovements[i], bs) : vertices[i];
    if (!extrudeByPath) {
      // 如果没有path 直接延申即可
      v(vert.x, vert.y, (depth / steps) * s);
    } else {
      // 这里为了计算当前step位置的外部边缘的一圈vertex坐标
      // 增加对应的向量数值
      const vertice3D = new Vector3(vert.x, vert.y, 0);
      position2.copy(vertice3D);
      // // 做相应的旋转变换
      position2.applyMatrix4(matrixList[s]).add(extrudePts[s]);
      v(position2.x, position2.y, position2.z);
    }
  }
}

首先1-12行，绘制首个shape面，其实就是将shape的所有绘制点挪到向量的起始点，这里是(0,0,0)。重点说明14-32行：循环变量s标识侧面绘制拉伸线条中细分线段的点的index，i标识shape的对应绘制点的index。由于extrudeByPath在我们的应用场景下总是有值，所以只用看23-30行代码。在这里，需要做一个rotation变换，用来处理sweep中出现向量方向偏转后的对应点的rotation。

const getMatrix = () => {
    if (splineTube.tangents.length === 0) {
      return [];
    }
    // 原始矩阵 后面矩阵都和该矩阵进行比较变换
    const m0 = new Matrix4();
    m0.makeBasis(splineTube.tangents[0], splineTube.normals[0], splineTube.binormals[0]);
    // compareMatrix = (mRot.m0)-1
    const compareMatrix = new Matrix4();
    compareMatrix.multiplyMatrices(mRot, m0).invert();
    const matrixList = splineTube.tangents.map((tangent, i) => {
      const normal = splineTube.normals[i];
      const binormal = splineTube.binormals[i];
      // 对应该点的Frenet坐标系变换
      const mi = new Matrix4();
      mi.makeBasis(tangent, normal, binormal);
      // 计算从m1->mi的变换 (mRot.mi).(mRot.m1)-1
      const retMatrix = new Matrix4();
      retMatrix.multiplyMatrices(mRot, mi).multiply(compareMatrix);
      return retMatrix;
    });
    return matrixList;
  };
  // 这个矩阵需要用于后面外围平面的变化计算
  matrixList = getMatrix();
}

计算曲线上对应点的rotation变换矩阵，仍然需要用到坐标系变换的知识。对于曲线路径上的任意一点，我们需要根据这个点的切向量的位置去确认它和起始点的切向量的偏移关系。但是考虑到所有的路径点都会受到mRot矩阵的作用，所以这个基的变换需要剔除掉mRot的影响。
这里的基变换很简单，首先初始点A基矩阵我们设为M1，然后路径中取任意点B其基矩阵为Mi，现在计算路径中的旋转矩阵。考虑A点在实际坐标系中受到mRot作用，mRot·M1，同理B点作用矩阵为mRot·Mi，这样要从A点切向量向量旋转到B点切向量需要矩阵作用为mRot·Mi(mRot·M1)-1，然后依次算出每个点对应的Matrix4，就可以获取所有路径上点的rotation对应的Matrix4。

现在回到计算侧面点的代码上来：

  const vertice3D = new Vector3(vert.x, vert.y, 0);
  position2.copy(vertice3D);
  // // 做相应的旋转变换
  position2.applyMatrix4(matrixList[s]).add(extrudePts[s]);
  v(position2.x, position2.y, position2.z);

实际上行1获取了shape的对应绘图点，然后行5将计算出的向量点位置获取到，然后和绘图点相加，实际上是将shape在rotation变换后平移到对应的向量位置。

处理转角

在路径分点时，对于每个转角代码中都会预留3个step，

curveLengths.forEach((curveLength, index) => {
  // 最后一条曲线（存储一点作为最后的连接点）
  if (index === curveLengths.length - 1) {
    return;
  }
  // 计算当前分curve的末端位置
  const rate = curveLength / allLength;
  // 前者对应前曲线末端 后者对应后曲线开端
  pointRate.push(rate - 1 / (100 * divisions));
  pointRate.push(rate);
  pointRate.push(rate + 1 / (100 * divisions));
  // 用于查找rate的index列表
  cornerRateList.push(rate);
});

现在代码将通过这3个step绘制连线。

当平面发生翻转后，如果不进行连接，就会产生不自然的连接，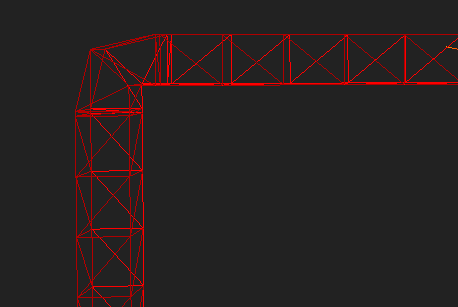

如果想要得到一个自然的连接，一个思路就是将反转的平面的对应点的延长线进行连接，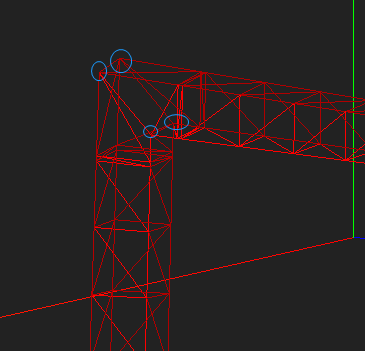

for (const cornerIndex of cornerIndexList) {
  // 前一个和后一个step位置 用于定位点
  const preStep = cornerIndex - 1;
  const nextStep = cornerIndex + 1;
  const preVector = splineTube.tangents[preStep].clone();
  const nextVector = splineTube.tangents[nextStep].clone();
  // 向量平行
  const dotVectorLen = new Vector3().copy(preVector).dot(nextVector);
  if (isEqual(dotVectorLen, 1)) {
    // 向量平行 这里跳过
    continue;
  }
  // 判断两个向量的相等 要求是差异点不会太大
  const isVertexEqual = (v1: Vector3, v2: Vector3) => {
    return Math.abs(v1.x - v2.x) < 0.00001 && Math.abs(v1.y - v2.y) < 0.00001 && Math.abs(v1.z - v2.z) < 0.00001;
  };
  // p1对应点1 v1对应线1向量 p2对应点2 v2对应线2向量
  // 具体原理查看 https://blog.csdn.net/xdedzl/article/details/86009147
  const getLineIntersection = (p1: Vector3, p2: Vector3, v1: Vector3, v2: Vector3) => {
    const startPointSeg = new Vector3().copy(p2).sub(p1);
    // 有向面积1，2
    const vecS1 = new Vector3().copy(v1).cross(v2);
    const vecS2 = new Vector3().copy(startPointSeg).cross(v2);
    const num = new Vector3().copy(startPointSeg).dot(vecS1);
    if (Math.abs(num) > Number.EPSILON) {
      console.log('直线不共面');
      // throw '直线不共面';
    }
    const rate = vecS2.dot(vecS1) / vecS1.lengthSq();
    const interSection = new Vector3().copy(v1).multiplyScalar(rate).add(p1);
    return interSection;
  };
  // 计算这些点中每两个点的交点
  for (let i = 0; i < vlen; i++) {
    // 拐点的前后两个面的对应点计算
    const preVertexIndex = vlen * preStep + i;
    const preVertex = new Vector3(
      placeholder[3 * preVertexIndex],
      placeholder[3 * preVertexIndex + 1],
      placeholder[3 * preVertexIndex + 2]
    );
    const nextVertexIndex = vlen * nextStep + i;
    const nextVertex = new Vector3(
      placeholder[3 * nextVertexIndex],
      placeholder[3 * nextVertexIndex + 1],
      placeholder[3 * nextVertexIndex + 2]
    );
    // 获取两个向量交点
    // 两个点实际上是一个点 不用计算
    if (isVertexEqual(preVertex, nextVertex)) {
      continue;
    }
    // 交点坐标计算
    const newPoint = getLineIntersection(preVertex, nextVertex, preVector, nextVector);
    // 更新坐标
    const vertexIndex = vlen * cornerIndex + i;
    placeholder[vertexIndex * 3] = newPoint.x;
    placeholder[vertexIndex * 3 + 1] = newPoint.y;
    placeholder[vertexIndex * 3 + 2] = newPoint.z;
  }
}

此处代码获取转角的前后平面，然后计算前后平面对应的位置的交点。然后替换掉原先计算好的侧面点。这里计算空间上直线的交点的算法可以参考[blog](https://blog.csdn.net/xdedzl/article/details/86009147)。

收尾

调用three.js的绘画侧面和地面的代码，完成geometry的创建，接着还原开始时的旋转，

// 还原
mGen.invert();
mVec.invert();
this.applyMatrix4(mGen);
this.applyMatrix4(mVec);

这样得到的geometry即给定参数对应的空间几何体。

优化

在设置参数时，有一个非常重要的参数steps，它决定了绘画geometry的粒度，steps越大绘画越精细。

step=30

step=120
如果是extrude即使steps=1也可以完成绘画，

而sweep正如上面所述，其由于有转角等处理，它的steps至少要满足一定条件。
绘制一个模型，经常需要成百上千的geometry，如果steps设置过大会让画面渲染变得非常卡顿，因此在类的实现中自动设置steps是一个很有必要的行为。

const createPath = () => {
    const path = new Path();
    const pathCoordinates = options.pathArr;
    if (pathCoordinates.length < 2) {
      throw new Error('path 太短');
    }
    let size = 3;
    let i = 0;
    while (i < pathCoordinates.length) {
      const startPoint = new Vector3(...pathCoordinates[i]);
      let j = i + 1;
      // 计算起始点到结束点的向量
      let subVector!: Vector3;
      // 合并连续的同方向向量
      while (j < pathCoordinates.length) {
        const endPoint = new Vector3(...pathCoordinates[j]);
        if (subVector === undefined) {
          // 最后两个点 成为一条直线
          if (j === pathCoordinates.length - 1) {
            const line = new LineCurve3(startPoint, endPoint);
            path.curves.push(line as any);
            size += 5;
            // 旧的点变为新的点
            i = j;
            // 最后一个点执行后直接结束
            i++;
            break;
          }
          subVector = new Vector3().subVectors(endPoint, startPoint);
          j++;
        } else {
          const newSubVector = new Vector3().subVectors(endPoint, startPoint);
          // 判断新老向量是否平行
          const crossVectorLenSq = new Vector3().crossVectors(subVector, newSubVector).lengthSq();
          if (isEqual(crossVectorLenSq, 0)) {
            // 最后一条直线
            if (j === pathCoordinates.length - 1) {
              const line = new LineCurve3(startPoint, endPoint);
              path.curves.push(line as any);
              size += 5;
              // 旧的点变为新的点
              i = j;
              // 最后一个点执行后直接结束
              i++;
              break;
            }
            // 向量平行继续
            j++;
          } else {
            // 向量不平行 增加path
            const line = new LineCurve3(startPoint, new Vector3(...pathCoordinates[j - 1]));
            path.curves.push(line as any);
            size += 5;
            // 旧的点变为新的点
            i = j - 1;
            break;
          }
        }
      }
    }
    options.extrudePath = path as any;
    options.steps = options.type === 'extrude' ? 3 : size;
  };

createPath函数，其目的是根据输入的pathArr生成一个Path实例。
首先，代码根据路径中的向量点判断新的点是否在老的向量上，如果是那么新的点作为输入路径向量的终点。举个例子:

const pathArr = [
  [0, 0, 0],
  [0, 1, 0],
  [0, 2, 0],
  [0, 2, 1]
];

首先取(0,0,0)作为起点，然后(0,1,0)作为终点，得到当前向量为(0,1,0)。不难发现(0,2,0)也在向量方向上，这时用(0,2,0)替换(0,1,0)作为向量终点，当前向量变为(0,2,0)。直到看到下一个点
(0,2,1)，不在该向量上，此时开始进入新的向量循环，同时把之前的向量(0,2,0)添加到路径中。
由于添加路径时产生了转角，对sizes进行定量增加。如果是曲线路径后续还需要进行其他的优化处理。
另外extrude需要的steps很少因此可以直接设置其steps为3。

TODO

对于曲线路径的处理，或者很多corner case的测试还没有完善，需要后续继续更新代码。

编程记录

在threejs上extrude与sweep实现