一、高阶函数
    一个接受函数参数的函数为高阶函数。
    不管是函数声明还是函数表达式，函数都指向一个变量。
    高阶函数的优点：
    （1）对函数内部功能进行抽象，可以传入自定义方法，还可以扩展功能。
    （2）函数参数可以作为函数执行后的回调函数执行

    1. let test = function(a, b, fn){
    2.     return fn(a) + fn(b)
    3. }
    5. function powFn(a){
    6.     return Math.pow(a,a)
    7. }
    9. let res = test(1,2,powFn)

    不是什么时候都硬要写高阶函数

    1. function test(a, b, fn){
    2.     return fn(a, b)
    3. }
    4. 这里的高阶函数的功能只是去调用computor, 没有自己的功能
    5. function computor(a, b){
    6.     return a + b
    7. }
    8. console.log(test(1,2,computor))

    如果一个高阶函数的功能只是调用另一个函数，就违背了函数单一功能的原则。

    1. funtion test (fn){
    2.     return doSth(function(data){
    3.       return fn(data)
    4.   })
    5. }
    7. function doSth(fn){
    8.     return fn()
    9. }
    11. function add (a,b){
    12.     return a + b
    13. }
    15. let myFn = test(add)
    16. myFn => doSth(function(data){ return add(data)}) => function(data){return add(data)}() => return add(data)

    二、函数柯理化
    js函数执行时，不关心是否传参或者参数个数类型。当函数需要完整参数才能执行时，柯理化就派上用场了。
    curry(add(1,2), 3,4) === curry(add(1), 2, 3, 4)，当参数没传够的时候，函数执行后返回一个函数，再接受参数，知道参数接收完成时，将函数汇总进行计算。
    特点：
    （1）简化代码，经过柯理化后，很多逻辑都封装在柯理化函数中，只有只需要传参。
    （2）提高维护性，柯理化函数返回的函数，是在一个函数体类产生，易维护。
    （3）功能单一化，一个函数体内可能由多个任务组成，需要将多个单一功能函数组合起来。

    1. function curry(fn){
    2.     let args = [].slice.call(arguments, 1);
    3.   return function(){
    4.       let innerArgs = Array.from(arguments),
    5.         combinedArgs = args.concat(innerArgs);
    6.             return fn.apply(this, combinedArgs)
    7.   }
    8. }
    9. function add(a,b,c,d){
    10.     return a + b + c + d
    11. }
    12. let cum1 = curry(add, 1),
    13.     cum2 = curry(add, 1,2);
    14. console.log(cum1(2,3,4))
    15. console.log(cum2(3,4))

    三、柯理化工具函数封装
    核心步骤，在没接受到足够数量参数时，不执行传入的原函数，返回具有参数判断功能、并包含已传参数的新函数；这个函数在执行时会判断累计的参数是否够数，如果不够则继续返回相同功能的新函数。

    1. function curryFunc(fn,length){
    2.   //fn第一次是工具函数，第二次是包含了已传参数的函数
    3.     let len = length || fn.length;
    4.   //len 来保存待接收参数个数，第一次调用时保存柯理化函数的形参个数，后面用来保存待接受参数个数
    6.   //单层函数柯理化方法
    7.   function singleStepCurry(foo){
    8.       let outterArgs = [].slice.call(arguments,1);
    9.     return function(){
    10.         let innerArgs =  [].slice.call(arguments),
    11.           combinedArgs = outterArgs.concat(innerArgs);
    12.       //最开始没有返回函数执行结果
    13.       return foo.apply(this,combinedArgs)
    14.     }
    15.     //处理以后，返回包含之前参数和原函数的新函数。
    16.   }
    18.   return function(){
    19.     let length = arguments.length,
    20.         currentArgs = Array.from(arguments),
    21.         formattedArr = [fn].concat(currentArgs);
    22.     //判断参数是否已经接受完毕
    23.       if(len > length){
    24.       console.log('len',len,'length',length)
    25.       let fnCurriedWithArgs = singleStepCurry.apply(this, formattedArr);
    26.       return curryFunc( fnCurriedWithArgs , len - length) 
    27.       // len - length为还需接受参数个数
    28.     }else{
    29.       //之前没有返回函数执行结果
    30.         return fn.apply(this, currentArgs)
    31.     }
    32.   }
    33. }
    35. function add (a,b,c,d,e){
    36.     return a + b + c + d + e
    37. }
    39. var computor = curryFunc(add);
    40. console.log(computor(1,2,3,4))
    1. function curry (fn, length){
    2.   //每次更新待接收参数
    3.     let len = length || fn.length; 
    5.   //单层柯理化工具函数
    6.   function singleStepCurry (fn){
    7.       let outterArgs = [...arguments].slice(1);   //没有把原函数排除
    8.     return function(){
    9.         let innerArgs = [...arguments],
    10.           accumulatedArgs = outterArgs.concat(innerArgs);
    11.       console.log(innerArgs,accumulatedArgs)
    12.       return fn.apply(this,accumulatedArgs)
    13.     }
    14.   }
    17.   return function(){
    18.       let currentArgs = Array.prototype.slice.call(arguments),
    19.         currentLength = currentArgs.length;
    20.     console.log(currentLength)
    21.     //判断参数是否够数如果参数没够，再执行一次单层柯理化
    22.     if(len > currentLength){
    23.         let formattedArr = [fn].concat(currentArgs),
    24.           curriedFunc = singleStepCurry.apply(this, formattedArr); //之前没有使用apply传了个数组
    25.       return curry(curriedFunc, len - currentLength)
    26.     }else{
    27.       //fn是每次记录之前参数的函数，里面也包含了原函数。
    28.       console.dir(fn)
    29.       return fn.apply(this, currentArgs)
    30.     }
    31.   }
    32. }
    34. function add (a,b,c,d,e){
    35.     return a + b + c + d + e
    36. }
    38. let addingComputor = curry(add);
    39. console.log(addingComputor(1)(2)(3)(4)(5))

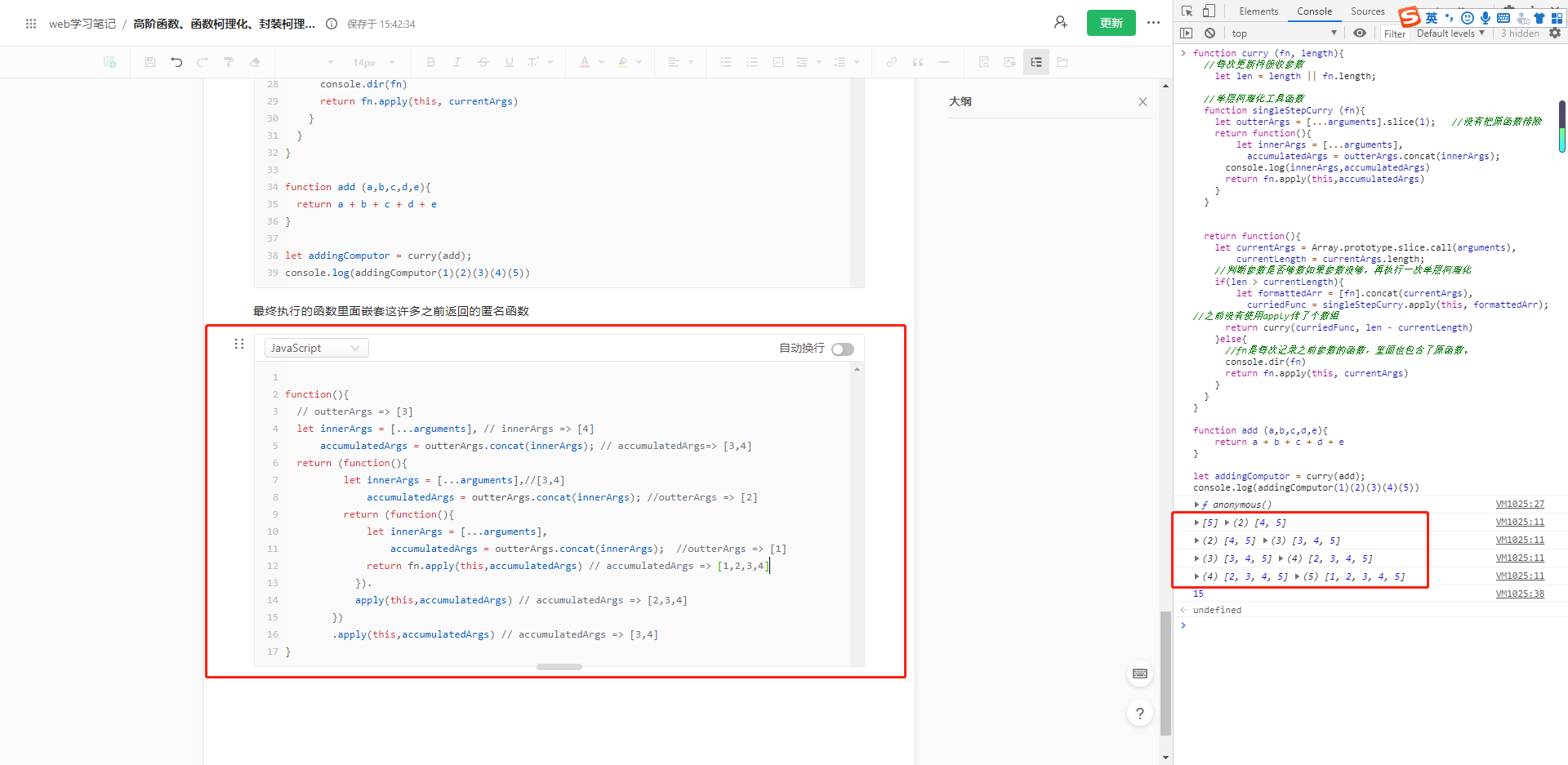
    最终执行的函数里面嵌套这许多之前返回的匿名函数

    2. function(){
    3.   // outterArgs => [3]
    4.   let innerArgs = [...arguments], // innerArgs => [4]
    5.       accumulatedArgs = outterArgs.concat(innerArgs); // accumulatedArgs=> [3,4]
    6.   return (function(){
    7.           let innerArgs = [...arguments],//[3,4]
    8.               accumulatedArgs = outterArgs.concat(innerArgs); //outterArgs => [2]
    9.           return (function(){
    10.               let innerArgs = [...arguments], 
    11.                   accumulatedArgs = outterArgs.concat(innerArgs);  //outterArgs => [1]
    12.               return fn.apply(this,accumulatedArgs) // accumulatedArgs => [1,2,3,4]
    13.             }).
    14.               apply(this,accumulatedArgs) // accumulatedArgs => [2,3,4]
    15.         })
    16.             .apply(this,accumulatedArgs) // accumulatedArgs => [3,4]
    17. }

    如下图：
    image.png