https://art-design-ui.github.io/data-structure-algorithm/guide/%E5%A0%86%E6%8E%92%E5%BA%8F

基本介绍

堆排序是利用 堆 这种 数据结构 而设计的一种排序算法，它是一种选择排序，最坏 、最好、平均时间复杂度均为 O(nlogn)，它是不稳定排序。
注意因为完全二叉树的性质，可以用数组表示对应的树结构（所以，堆排序过程中，你是看不到树这数据结构的，用数组进行映射了），这叫顺序存储

顺序存储二叉树

特点

  • 第 n 个元素的 左子节点 为 2*n+1
  • 第 n 个元素的 右子节点 为 2*n+2
  • 第 n 个元素的 父节点 为 (n-1)/2
  • 最后一个非叶子节点为 Math.floor(arr.length/2)-1

堆是具有以下性质的完全二叉树：

  • 大顶堆：每个节点的值都 大于或等于 其左右孩子节点的值注：没有要求左右值的大小关系
  • 小顶堆：每个节点的值都 小于或等于 其左右孩子节点的值

    基本思想

  1. 将待排序序列构造成一个大顶堆注意：这里使用的是数组，而不是一颗二叉树
  2. 此时：整个序列的 最大值就是堆顶的根节点
  3. 将其 与末尾元素进行交换，此时末尾就是最大值
  4. 然后将剩余 n-1 个元素重新构造成一个堆，这样 就会得到 n 个元素的次小值。如此反复，便能的得到一个有序序列。

    堆排序介绍

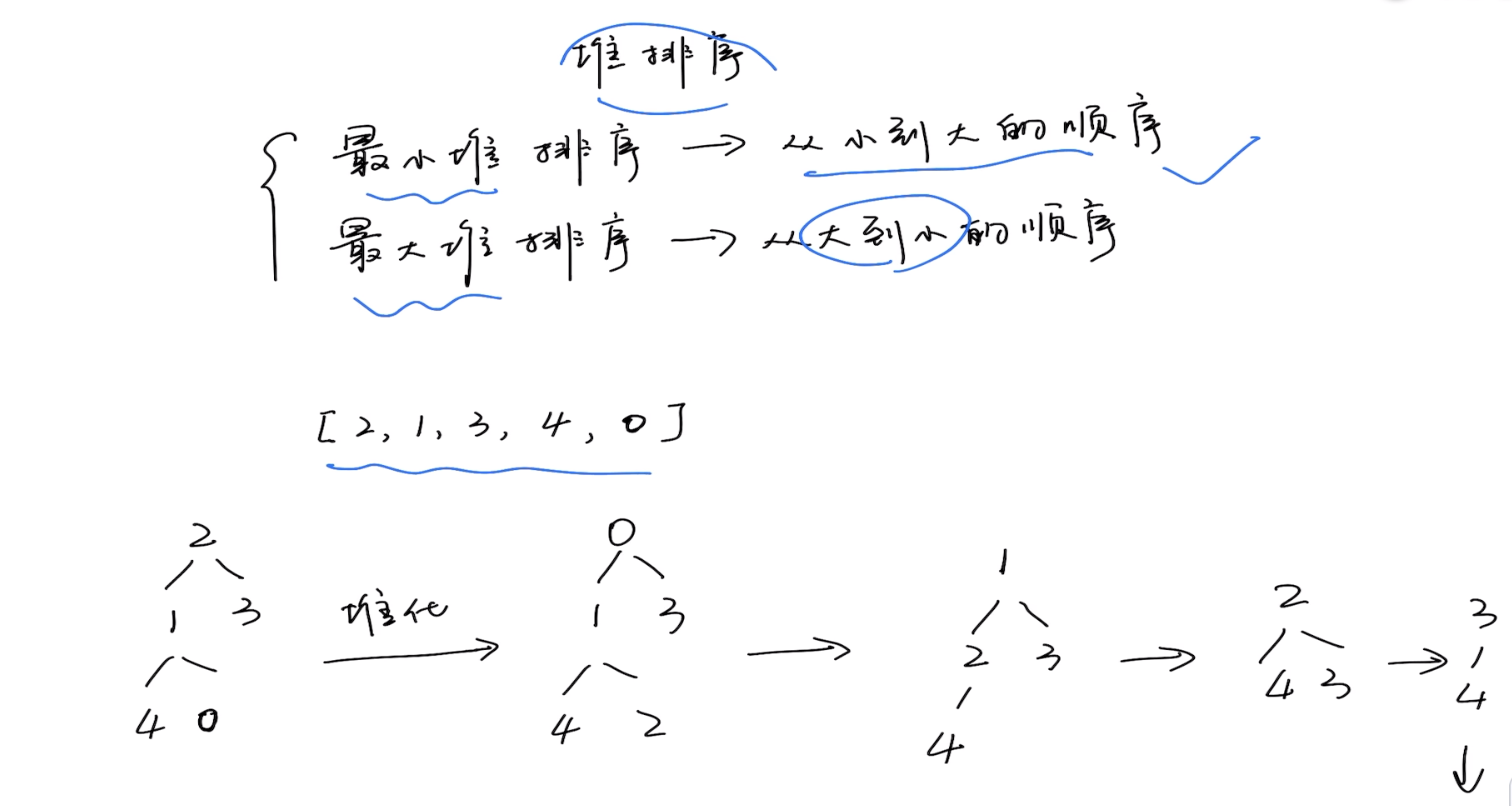
    image.png

    第一步：构造堆结构

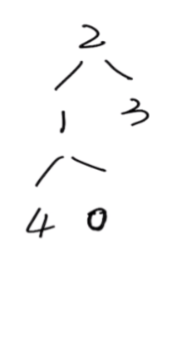
    image.png

第二步：堆化变成最小（大）堆

从最后一个非叶子（有孩子的节点）节点开始调整，从左到右，从上到下进行调整。
发现他（1）的孩子（0）比他小，就和孩子交换位置，[2，0，3，4，1]
在从这个非叶子节点（0）的位置向上查看，发现他的父节点（2）比他大就交换位置，[0，2，3，4，1]
交换后的堆结构中，依然看这个非叶子节点（2）的位置，发现他的孩子（1）比他小，再次交互位置，[0，1，3，4，2]
堆化的过程就是让非叶子节点的值比他的孩子节点的值小（大）。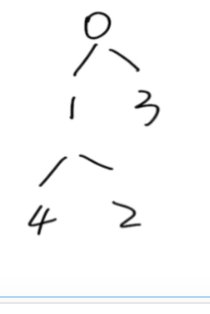
image.png

第三步：将堆顶元素与末尾元素进行交换

将堆顶元素与末尾元素进行交换，使其末尾元素最大。然后继续调整，再将堆顶元素与末尾元素交换，得到第二大元素。如此反复进行交换、重建、交换。

获取到对顶元素，记录并删除；
将最后一个位置上的值替换到堆顶，此时堆中的结构就是 [ 2, 1, 3, 4,]；
再将堆顶元素（2）和他的孩子节点（1，3）比较，与最小的孩子节点进行互换，此时[1, 2, 3, 4]；
交换完以后的节点（2）再和他下面的孩子节点比较，发现 4比他大，正好符合最小堆，不用交互了。得到了新的堆 [1, 2, 3, 4]；
重复上述步骤，直到堆中只剩最后一个元素就结束。

总结思路

  1. 将无序序列构建成一个堆，根据升序降序需求选择大顶堆
  2. 将堆顶元素与末尾元素交换，将最大元素「沉」到数组末端
  3. 重新调整结构，使其满足堆定义，然后继续交换堆顶与当前末尾元素，反复执行调整、交换步骤，直到整个序列有序。

    代码模板

    1. /**
    2. * @param {number[]} nums
    3. * @param {number} k
    4. * @return {number}
    5. */
    6. // 整个流程就是上浮下沉
    7. var findKthLargest = function(nums, k) {
    8. let heapSize=nums.length
    9.  buildMaxHeap(nums,heapSize) // 1.构建好了一个大顶堆
    10.  // 2.进行下沉 大顶堆是最大元素下沉到末尾
    11.  for(let i=nums.length-1;i>=nums.length-k+1;i--){
    12.      swap(nums,0,i)
    13.      --heapSize // 下沉后的元素不参与到大顶堆的调整
    14.      // 重新调整大顶堆
    15.       maxHeapify(nums, 0, heapSize);
    16.  }
    17.  return nums[0]
    18. // 从最后一个非叶子节点开始自下而上构建一颗大顶堆
    19. function buildMaxHeap(nums,heapSize){
    20.   for(let i=Math.floor(heapSize/2)-1;i>=0;i--){
    21.      maxHeapify(nums,i,heapSize)
    22.   }
    23. }
    24. // 第i个元素和他的左右子节点比较，互换位置，构建过程和下沉过程都需要比较
    25. function maxHeapify(nums,i,heapSize){
    26.     let l=i*2+1
    27.     let r=i*2+2
    28.     let largest=i
    29.     if(l < heapSize && nums[l] > nums[largest]){
    30.         largest=l
    31.     }
    32.     if(r < heapSize && nums[r] > nums[largest]){
    33.         largest=r
    34.     }
    35.     if(largest!==i){
    36.         swap(nums,i,largest) // 进行节点调整
    37.         // 继续调整下面的非叶子节点
    38.         maxHeapify(nums,largest,heapSize)
    39.     }
    40. }
    41. function swap(a,  i,  j){
    42.      let temp = a[i];
    43.      a[i] = a[j];
    44.      a[j] = temp;
    45. }
    46. };

    复杂度分析

    堆化复杂度是 O(N)，
    排序：N个堆顶元素，每一个删除操作的复杂是 logN，
    所以总共复杂度是 O(logN)
    空间复杂度：堆里面有N个元素，所以O(N)