516. 最长回文子序列

难度中等
给定一个字符串 s ，找到其中最长的回文子序列，并返回该序列的长度。可以假设 s 的最大长度为 1000 。

示例 1:
输入:
“bbbab”
输出:
4
一个可能的最长回文子序列为 “bbbb”。
示例 2:
输入:
“cbbd”

输出:
2
一个可能的最长回文子序列为 “bb”。

  1. class Solution {
  2.     public int longestPalindromeSubseq(String s) {
  3.         int n = s.length();
  4.         int[][] f = new int[n][n];
  5.         for (int i = n - 1; i >= 0; i--) {
  6.         //for (int i = 1; i <n; i++) { //为什么不行？   
  7.             f[i][i] = 1;
  8.             for (int j = i + 1; j < n; j++) {
  9.                 if (s.charAt(i) == s.charAt(j)) {
  10.                     f[i][j] = f[i + 1][j - 1] + 2;
  11.                 } else {
  12.                     f[i][j] = Math.max(f[i + 1][j], f[i][j - 1]);
  13.                 }
  14.             }
  15.         }
  16.         return f[0][n - 1];
  17.     }
  19. // 作者：a380922457
  20. // 链接：https://leetcode-cn.com/problems/longest-palindromic-subsequence/solution/dong-tai-gui-hua-si-yao-su-by-a380922457-3/
  22. }

解题思路：

状态
f[i][j] 表示 s 的第 i 个字符到第 j 个字符组成的子串中，最长的回文序列长度是多少。
转移方程
如果 s 的第 i 个字符和第 j 个字符相同的话
f[i][j] = f[i + 1][j - 1] + 2
如果 s 的第 i 个字符和第 j 个字符不同的话
f[i][j] = max(f[i + 1][j], f[i][j - 1])
然后注意遍历顺序，i 从最后一个字符开始往前遍历，j 从 i + 1 开始往后遍历，这样可以保证每个子问题都已经算好了。
初始化
f[i][i] = 1 单个字符的最长回文序列是 1
结果
f[0][n - 1]

作者：a380922457
链接：https://leetcode-cn.com/problems/longest-palindromic-subsequence/solution/dong-tai-gui-hua-si-yao-su-by-a380922457-3/

首先明确一下 base case，如果只有一个字符，显然最长回文子序列长度是 1，也就是 dp[i][j] = 1 (i == j)。
因为 i 肯定小于等于 j，所以对于那些 i > j 的位置，根本不存在什么子序列，应该初始化为 0。

另外，看看刚才写的状态转移方程，想求 dp[i][j] 需要知道 dp[i+1][j-1]，dp[i+1][j]，dp[i][j-1] 这三个位置；再看看我们确定的 base case，填入 dp 数组之后是这样：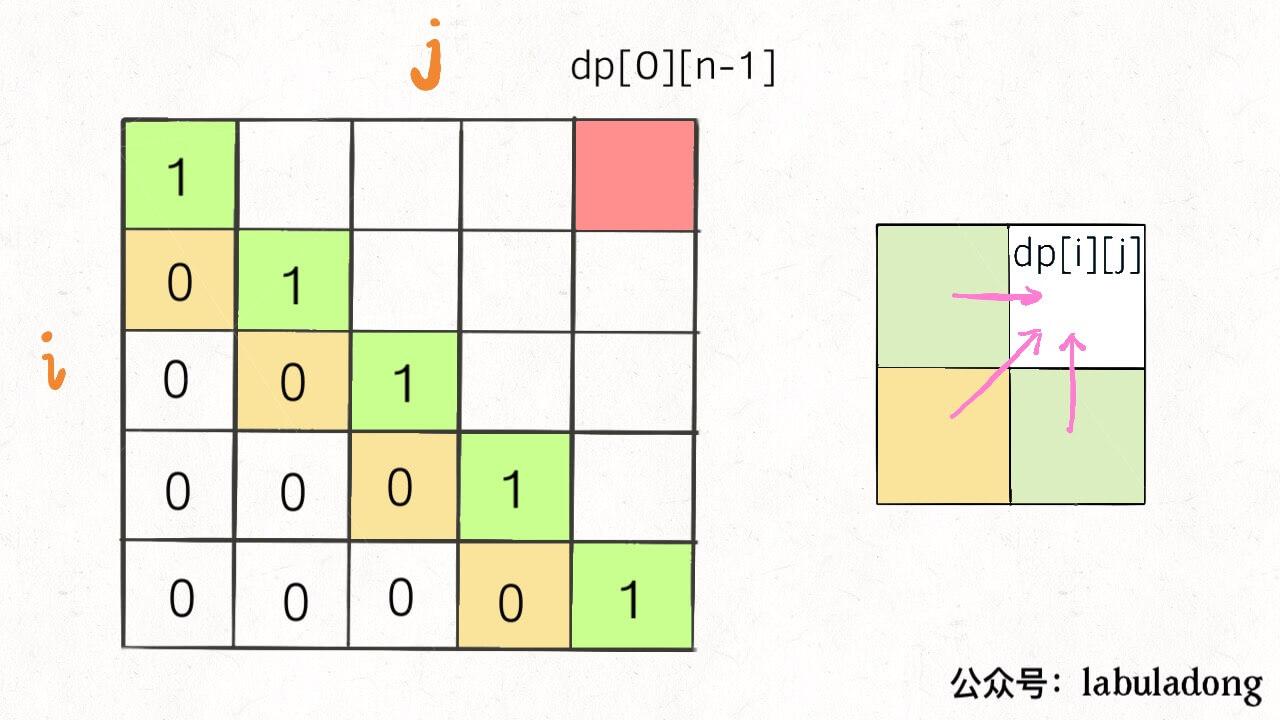
image.png
作者：labuladong
链接：https://leetcode-cn.com/problems/longest-palindromic-subsequence/solution/zi-xu-lie-wen-ti-tong-yong-si-lu-zui-chang-hui-wen/