153. 寻找旋转排序数组中的最小值

  1. class Solution {
  2.     public int findMin(int[] nums) {
  4.         // If the list has just one element then return that element.
  5.         if (nums.length == 1) {
  6.             return nums[0];
  7.         }
  9.         // initializing left and right pointers.
  10.         int left = 0, right = nums.length - 1;
  12.         // if the last element is greater than the first element then there is no rotation.
  13.         // e.g. 1 < 2 < 3 < 4 < 5 < 7. Already sorted array.
  14.         // Hence the smallest element is first element. A[0]
  15.         if (nums[right] > nums[0]) {
  16.             return nums[0];
  17.         }
  19.         // Binary search way
  20.         while (right >= left) {
  21.             // Find the mid element
  22.             int mid = left + (right - left) / 2;
  24.             // if the mid element is greater than its next element then mid+1 element is the smallest
  25.             // This point would be the point of change. From higher to lower value.
  26.             if (nums[mid] > nums[mid + 1]) {
  27.                 return nums[mid + 1];
  28.             }
  30.             // if the mid element is lesser than its previous element then mid element is the smallest
  31.             if (nums[mid - 1] > nums[mid]) {
  32.                 return nums[mid];
  33.             }
  35.             // if the mid elements value is greater than the 0th element this means
  36.             // the least value is still somewhere to the right as we are still dealing with elements
  37.             // greater than nums[0]
  38.             if (nums[mid] > nums[0]) {
  39.                 left = mid + 1;
  40.             } else {
  41.                 // if nums[0] is greater than the mid value then this means the smallest value is somewhere to
  42.                 // the left
  43.                 right = mid - 1;
  44.             }
  45.         }
  46.         return -1;
  47.     }
  49. // 作者：LeetCode
  50. // 链接：https://leetcode-cn.com/problems/find-minimum-in-rotated-sorted-array/solution/xun-zhao-xuan-zhuan-pai-lie-shu-zu-zhong-de-zui-xi/
  51. }

复杂度分析

  • 时间复杂度：和二分搜索一样 O(log⁡N)
  • 空间复杂度：O(1)

    分析

    如果数组没有被旋转，是升序排列，就满足 last element > first element。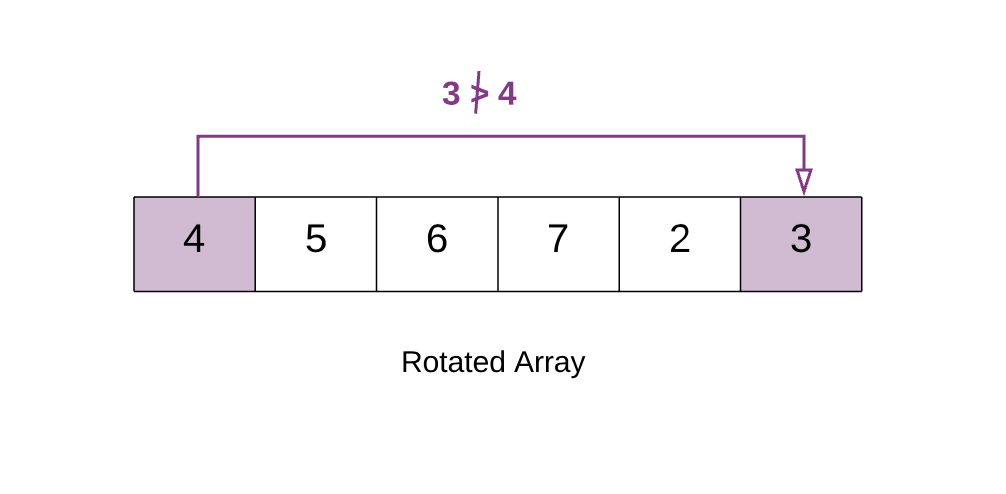
    image.png
    上面的例子中 3 < 4，因此数组旋转过了。这是因为原先的数组为 [2, 3, 4, 5, 6, 7]，通过旋转较小的

[2, 3] 移到了后面，也就是 [4, 5, 6, 7, 2, 3]。因此旋转数组中第一个元素 [4] 变得比最后一个元素大。

这意味着在数组中你会发现一个变化的点，这个点会帮助我们解决这个问题，我们称其为变化点。

在这个改进版本的二分搜索算法中，我们需要找到这个点。下面是关于变化点的特点：

所有变化点左侧元素 > 数组第一个元素

所有变化点右侧元素 < 数组第一个元素

算法

找到数组的中间元素 mid。
如果中间元素 > 数组第一个元素，我们需要在 mid 右边搜索变化点。
如果中间元素 < 数组第一个元素，我们需要在 mid 左边搜索变化点。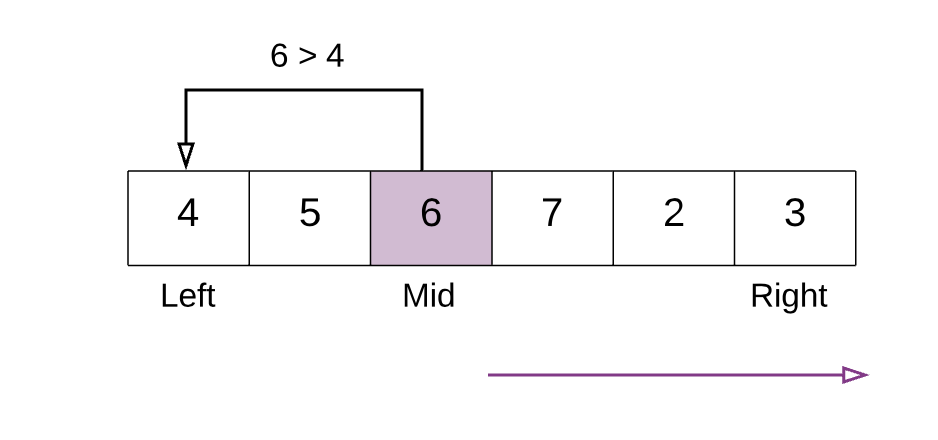
image.png
上面的例子中，中间元素 6 比第一个元素 4 大，因此在中间点右侧继续搜索。

当我们找到变化点时停止搜索，当以下条件满足任意一个即可：
nums[mid] > nums[mid + 1]，因此 mid+1 是最小值。
nums[mid - 1] > nums[mid]，因此 mid 是最小值。

作者：LeetCode
链接：https://leetcode-cn.com/problems/find-minimum-in-rotated-sorted-array/solution/xun-zhao-xuan-zhuan-pai-lie-shu-zu-zhong-de-zui-xi/