一元线性回归模型它所针对的是数据拥有一个特征变量的情况。
但绝大多数情况下,数据一般都会拥有多个特征。那对于这类数据我们需要的是多元线性回归模型。除了特征的个数,多元线性回归和一元线性回归本质上其实是没有太大的区别。
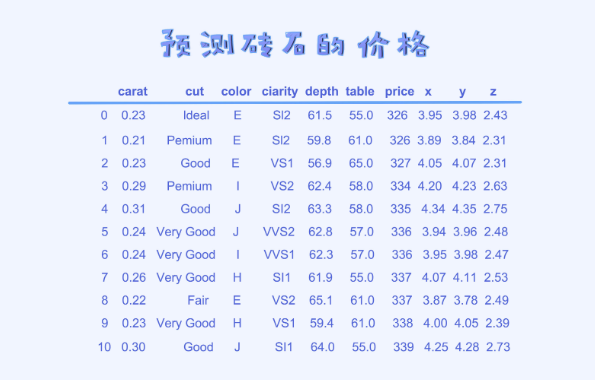
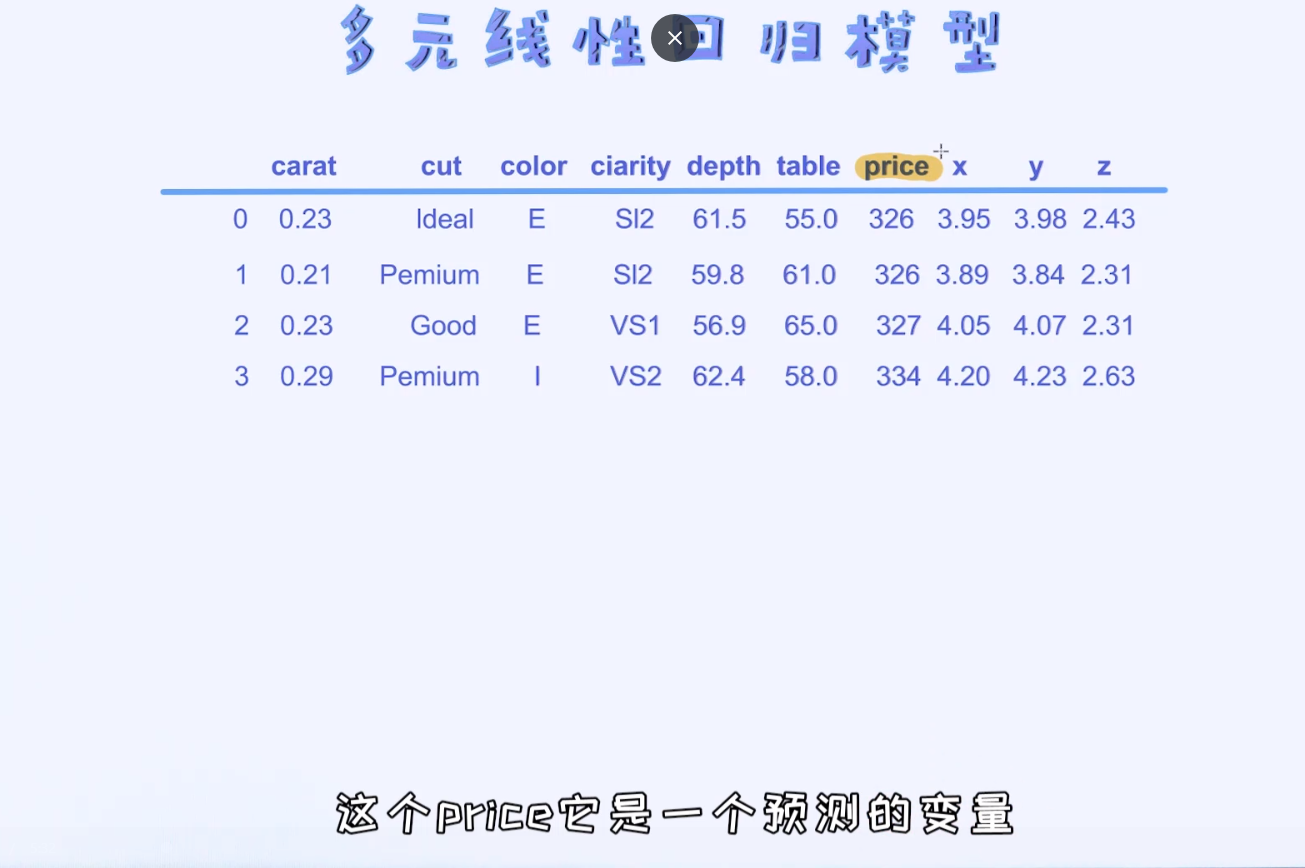
上面的表格里提供了一份数据。它的目的是通过砖石的各个特性来预测其价格。尝试使用多元线性回归来拟合这份数据。
在多元线性回归模型里,对于每一个特征,我们都会给它分配对应的参数。我们也可以把参数理解成是对于某一个特征的重要性。
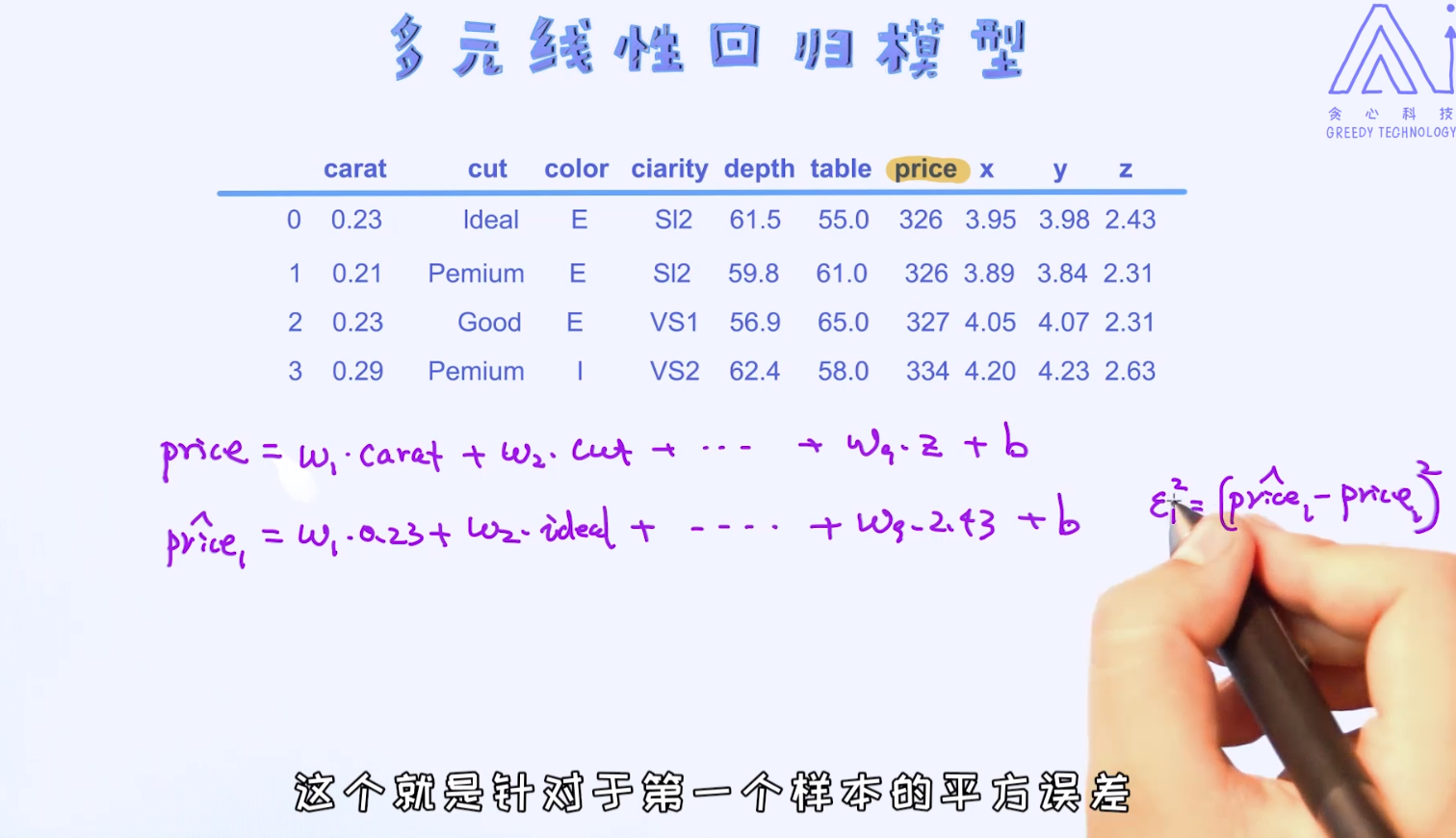
以此类推算出多元线性回归模型的损失函数
等训练完模型之后,我们即可以通过学出来的参数来解释哪些特征是重要的哪些是次要的。
如何求解多元线性回归模型的最优解。 这里需要涉及到线性代数相关的知识点
回顾一下什么是向量(Vector)、什么是矩阵(Matrix)以及什么是张量(Tensor)?
标量是一个具体的值,是一维的
向量是有方向的,可以看作是一个一维的数组。例如,三维向量: 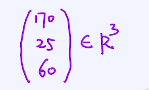
矩阵可以看作二维的数组,也可以理解为多个向量的集合
张量,二维以上的数组统称为张量的形式,例如把多个矩阵叠加在一起

向量的基本的知识点:
转置: 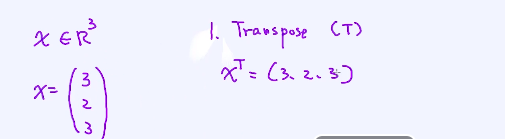
把一个列向量转为了横向量
加法、乘法:
矩阵的一些特性:
转置、加法、乘法:
乘法要满足矩阵大小的限制:
例如3x2的矩阵,一定是与2 x?的一个矩阵相乘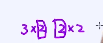 ,最终结果也是3x2的矩阵
,最终结果也是3x2的矩阵
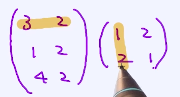 3x1+2x2
3x1+2x2 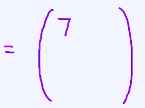
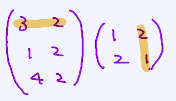 3x2+2x1
3x2+2x1 
 1x1+2x2
1x1+2x2
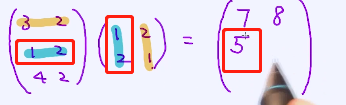
最终为:
下一个例子:(Z是一个向量但是也可以写成矩阵的格式)

最终x、y、z的相乘为:
可以先两两相乘,进行计算。
单位矩阵:对角线是1,其它位置都为0 ,通过I表示。例子: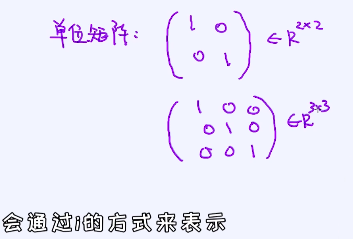
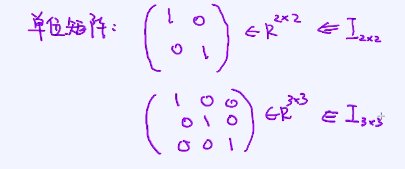
矩阵求逆过程(inverse):
python中INV操作就是矩阵求逆
一个x乘上x的逆矩阵会等于单位矩阵 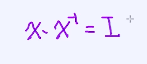
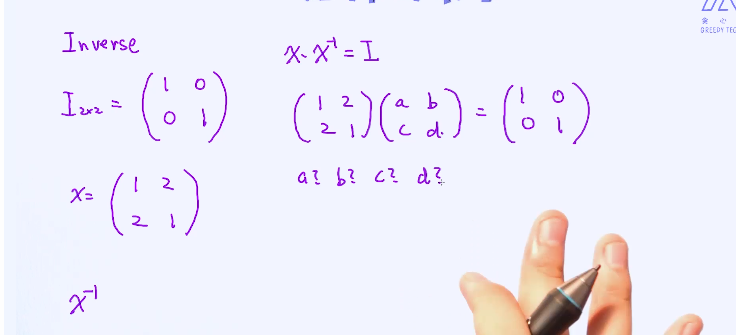
求解逆矩阵是非常耗时间的,要想办法找一个便捷的方法,有时候也不保证一定就存在逆矩阵
假设矩阵的行列式(determinant)等于0的话,这个矩阵是没有逆矩阵的
知道什么叫向量的范数(Vector Norm)。因为表示线性回归损失函数的时候会用到范数的概念。

必要的知识点已经全部了解完毕! 我们接着回到线性回归的模型当中,并尝试使用矩阵、向量的方式来描述它的损失函数。
http://asset.greedyai.com/course/RGZNXLY/videos-ch5-MSE_vector_matrix.mp4



对于上述的损失函数,如何去求解参数WW呢? 答案仍然跟之前一样:把导数设置为零!
这里的难点在于如何对向量和矩阵求导,这其实比较难。常用的方法是借助于求导法则,有一个非常实用的资料供大家参考,只要遇到跟向量、矩阵相关的求导,答案都可以从资料里查到: http://www2.imm.dtu.dk/pubdb/views/edoc_download.php/3274/pdf/imm3274.pdf
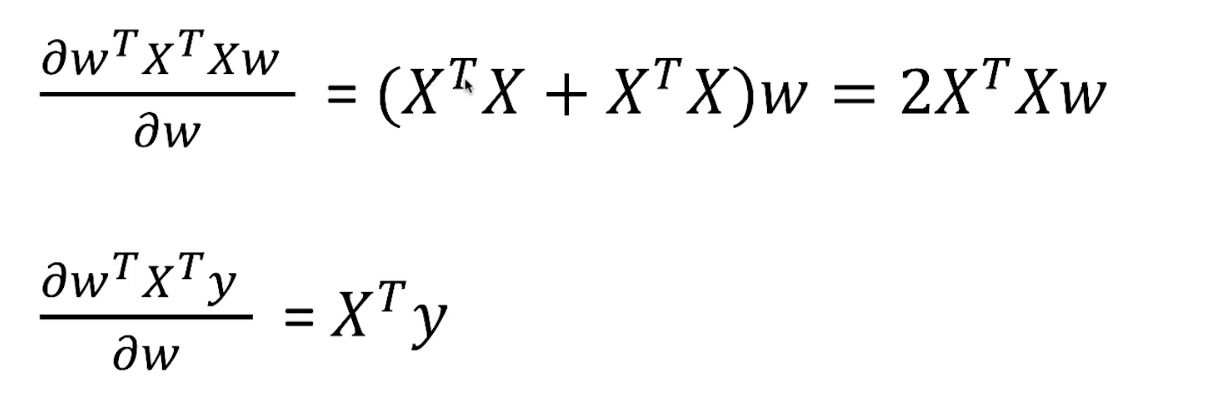
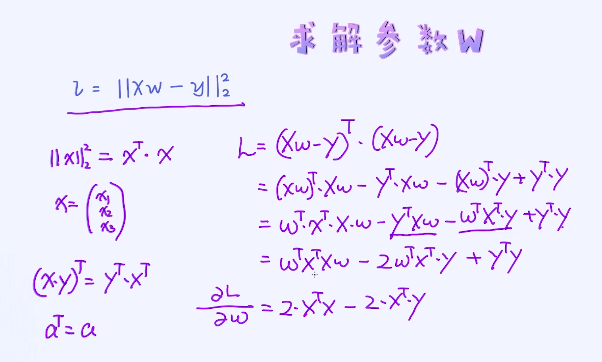


动手实现一下多元线性回归:任务描述
在这里,你需要实现一元线性回归模型的参数求解,参数分别是斜率和偏移量。这里需要把偏移量加入到参数里。假如原始特征为x, 那这时候需要通过[1,x]来表示新的特征。
import numpy as npfrom sklearn.linear_model import LinearRegression# 生成样本数据, 特征维度为2X = np.array([[1, 1], [1, 2], [2, 2], [2, 3]])# y = 1 * x_0 + 2 * x_1 + 3y = np.dot(X, np.array([1, 2])) + 3# 先使用sklearn自带的库来解决model = LinearRegression().fit(X, y)# 打印参数以及偏移量(bias)print ("基于sklearn的线性回归模型参数为 coef: ", model.coef_, " intercept: %.5f" %model.intercept_)# 手动实现参数的求解。先把偏移量加到X里a = np.ones(X.shape[0]).reshape(-1,1)X = np.concatenate((a, X), axis=1)# 通过矩阵、向量乘法来求解参数, res已经包含了偏移量res = np.matmul(np.linalg.inv(np.matmul(X.T, X)), np.matmul(X.T, y))# 打印参数以偏移量(bias)print ("通过手动实现的线性回归模型参数为 coef: ", res[1:], " intercept: %.5f"%res[0])

代码里我们使用了两组不同的数据。对于第一组数据运行一切正常,然而对于第二组数据出现了一点点小问题。通过控制台返回的消息试着理解一下到底发生了什么情况。

问题出现在了矩阵求逆的过程。我们要知道对于一个矩阵,我们并不能保证一定会算出其逆矩阵。
那到底什么时候矩阵会出现不可逆的情况呢? 答案是,特征之间线性相关的时候! 第二组数据中,其中两列的特征是线性相关的,所以这时候就出现了矩阵不可逆的现象。
接下来我们从数学的角度来分析出现此问题的原因。
第一、什么时候矩阵不可逆
答案是它的行列式(Determinant)为0的时候。
第二、那什么时候行列为等于0呢
答案是矩阵为非满秩矩阵(full rank matrix)的时候。
第三、那什么时候矩阵为非满秩呢
答案是矩阵中存在线性相关的时候,也就是特征之间存在强烈的线性相关,就像上面的第二个例子。
接着就得想有没有什么好的方法可以解决这个问题了。 能否想出解决方案呢?
(1)把线性相关的特征去掉,保证数据中不会出现线性相关的特征。(直接在数据处理阶段做预处理并保证没有任何的线性相关性的特征。)
(2)可以在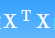 的基础上加一个单位矩阵
的基础上加一个单位矩阵
只要加上单位矩阵,我们即可以保证矩阵的可逆性,这是非常有效的方法。
其实加上这一项跟加一个正则项起到的作用是一样的
到目前为止,我们碰到的所有优化问题皆可以通过把导数设置为零的方式来求解。 这种方法也叫做解析解(Analytic Solution)。
除了上面提到了方法,还有什么方法可以用来求出最优解呢? 其中著名的算法叫作梯度下降法(Gradient Descent),它是一个循环迭代式的算法。另外,在线性回归中,它不受特征之间线性相关的影响。

