大数据的利器：随机梯度下降法

梯度下降法是一个非常经典的优化算法，但实际工程项目中梯度下降法的应用其实并不是特别多。这又为什么呢？ 这说明背后必然有个原因。 那这个原因到底是什么？

梯度下降法最大的问题：需要依赖于每次参数的更新，依赖于所有的样本

为了解决这个时间复杂度问题，我们最常用的算法其实是随机梯度下降法，可以理解成是梯度下降法的一个变种。

随机梯度下降法的核心思想是：每一次的迭代更新不再依赖于所有样本的梯度之和，而是仅仅依赖于其中一个样本的梯度。所以这种方法的优势很明显，通过很“便宜”的方式获得梯度，并频繁地对参数迭代更新。

这种频繁的更新，可以使得参数在更短的时间内达到收敛的效果。接着具体来理解一下随机梯度下降法的细节。

虽然这种方法用很低的成本即可以更新到模型的参数，但也有自身的缺点。由于仅仅根据一个样本来计算梯度，这里最大的问题是梯度的噪声。当我们使用梯度下降法时，梯度的计算是依赖于所有样本的，但随机梯度下降法的梯度计算仅仅依赖于其中的一个样本。这必然会导致计算出来的结果包含大量的噪声，因为我们试图使用一个样本的梯度来替换所有样本的梯度之和。

这种噪声会对参数的更新产生负面影响，使得每一次的迭代更新可能不太稳定。

所以呢，在随机梯度下降法的模式下，我们通常会把学习率设置为比较小的值，这样可以有效削弱梯度计算中带来的不稳定性。

相比梯度下降法，当我们使用随机梯度下降法的时候可以看到每一次迭代之后的目标函数或者损失函数会有一些波动性。有一些更新会带来目标值的提升，但有些更新反而让目标值变得更差。但只要实现细节合理，大的趋势是沿着好的方向而发展的。

目前来看，梯度下降法和随机梯度下降法分别可以看作是两个极端。前者考虑所有的样本，后者仅仅考虑其中的一个样本。有些犀利的朋友可能自然会问到：既然这两个极端各有优缺点，那是否可以使用一个折中的方案呢？

确实有一个折中的方案，叫做mini-batch gradient descent。它不依赖于所有的样本，但也不依赖于仅仅一个样本，而是它从所有样本中随机挑选一部分样本来计算梯度并更新参数。

从上述图里可以看得到批量梯度下降法做了一个折中，每次都是随机采样一部分样本然后做梯度的更新。这种做法会让每次的梯度计算既稳定效率也高，相当于结合了两者各自的优势。

下面的代码用来实现基于梯度下降法的逻辑回归。这里可能需要思考的是如何把循环的代码写成矩阵、向量的形式。提示：对于数据的采样，请参考numpy里的choice函数。 注意：每一次的梯度之和是采样过的样本中计算出来的。

# 导入相应的库
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
# 随机生成样本数据。 二分类问题，每一个类别生成5000个样本数据
np.random.seed(12)
num_observations = 5000
x1 = np.random.multivariate_normal([0, 0], [[1, .75],[.75, 1]], num_observations)
x2 = np.random.multivariate_normal([1, 4], [[1, .75],[.75, 1]], num_observations)
X = np.vstack((x1, x2)).astype(np.float32)
y = np.hstack((np.zeros(num_observations),
                              np.ones(num_observations)))
print (X.shape, y.shape)
# 数据的可视化
plt.figure(figsize=(12,8))
plt.scatter(X[:, 0], X[:, 1],
            c = y, alpha = .4)
# 实现sigmoid函数
def sigmoid(x):
    return 1 / (1 + np.exp(-x))
# 计算log likelihood
def log_likelihood(X, y, w, b):
    """
    针对于所有的样本数据，计算（负的）log likelihood，也叫做cross-entropy loss
    这个值越小越好
    X: 训练数据（特征向量）， 大小为N * D
    y: 训练数据（标签），一维的向量，长度为D
    w: 模型的参数， 一维的向量，长度为D
    b: 模型的偏移量，标量
    """
    # 首先按照标签来提取正样本和负样本的下标
    pos, neg = np.where(y==1), np.where(y==0)  
    # 对于正样本计算 loss, 这里我们使用了matrix operation。 如果把每一个样本都循环一遍效率会很低。 
    pos_sum = np.sum(np.log(sigmoid(np.dot(X[pos], w)+b)))
    # 对于负样本计算 loss
    neg_sum = np.sum(np.log(1-sigmoid(np.dot(X[neg], w)+b)))
    # 返回cross entropy loss
    return -(pos_sum + neg_sum)
# 实现逻辑回归模型
def logistic_regression_minibatch(X, y, num_steps, learning_rate):
    """
    基于梯度下降法实现逻辑回归模型
    X: 训练数据（特征向量）， 大小为N * D
    y: 训练数据（标签），一维的向量，长度为D
    num_steps: 梯度下降法的迭代次数
    learning_rate: 步长
    如果对于这块不是很熟悉，建议再看一下梯度下降法的推导视频 ^^
    """
    w, b = np.zeros(X.shape[1]), 0
    for step in range(num_steps):
        # 随机采样一个batch, batch大小为100
        batch = np.random.choice(X.shape[0], 100)
        X_batch, y_batch = X[batch], y[batch]
        # 计算预测值与实际值之间的误差
        error = sigmoid(np.dot(X_batch,w)+b) - y_batch
        # 对于w, b的梯度计算
        grad_w = np.matmul(X_batch.T, error)
        grad_b = np.sum(error)
        # 对于w, b的梯度更新
        w = w - learning_rate * grad_w
        b = b - learning_rate * grad_b
        # 每隔一段时间，计算一下log likelihood，看看有没有变化
        # 正常情况下， 它会慢慢变小，最后收敛
        if step % 10000 == 0:
            print (log_likelihood(X, y, w, b))
    return w,b
w, b = logistic_regression_minibatch(X, y, num_steps = 500000, learning_rate = 5e-4)
print ("(自己写的)逻辑回归的参数w, b分别为: ", w, b)
# 这里我们直接调用sklearn的模块来训练，看看跟自己手写的有没有区别。如果结果一样就说明是正确的！ 
from sklearn.linear_model import LogisticRegression
# C设置一个很大的值，意味着不想加入正则项 （在第七章会看到正则作用，这里就理解成为了公平的比较）
clf = LogisticRegression(fit_intercept=True, C = 1e15)
clf.fit(X, y)
print ("(sklearn)逻辑回归的参数w, b分别为: ", clf.coef_, clf.intercept_, )

输出结果
(10000, 2) (10000,)
6447.550681253917
241.09039607409554
194.7382047636013
176.76175911329608
167.20654548690686
161.19297550253066
157.09658903588695
154.1238989905663
151.90811731680515
150.28724287003558
148.77032310195239
147.6456191387174
146.75531534794337
146.01390911255515
145.31277976263198
144.79126567856957
144.29121842434913
143.9048861063236
143.7149004822943
143.24105500234361
143.02901232279285
142.77678818148974
142.6603577681975
142.42393449638
142.27066047698324
142.12544476805266
141.96569312300358
141.85525298340735
141.74246463134745
141.70696807083846
141.56701855913207
141.51700139426407
141.5729198779951
141.40338533702123
141.3188876292371
141.2554351383799
141.26707979275275
141.17450290886202
141.1990838772249
141.13121485730065
141.09306266369208
141.05510281971468
141.12958899212416
140.9918302034866
140.99246017507187
140.9561616298006
140.97511018161578
140.9500801882637
140.9071965810703
140.90564665934647
(自己写的)逻辑回归的参数w, b分别为: [-4.88153788 7.97863031] -13.58697811555371
/home/anaconda/anaconda3/lib/python3.7/site-packages/sklearn/linear_model/logistic.py:432: FutureWarning: Default solver will be changed to ‘lbfgs’ in 0.22. Specify a solver to silence this warning.
FutureWarning)
(sklearn)逻辑回归的参数w, b分别为: [[-5.02712572 8.23286799]] [-13.99400797]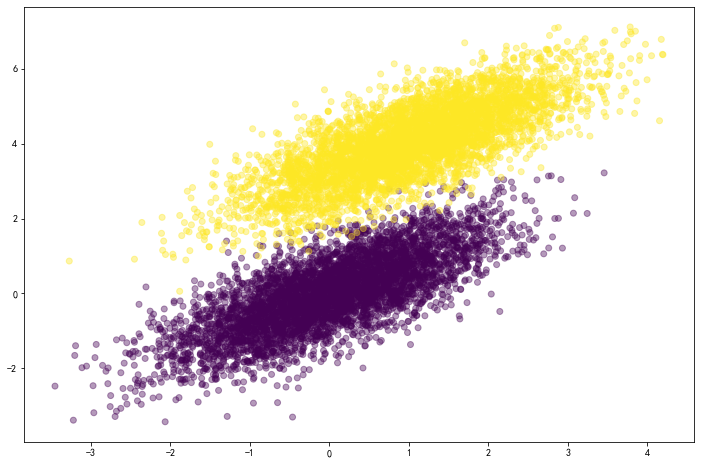

了解完了mini-batch梯度下降法，我们最后还是做一个比较吧，把这三种方式横向地对比一下。

M是人工定义的

其实梯度的噪声也有一些好处。特别是对于那些复杂模型的训练，噪声也可以使得我们可以得到更好的局部最优解。这又如何去理解呢？

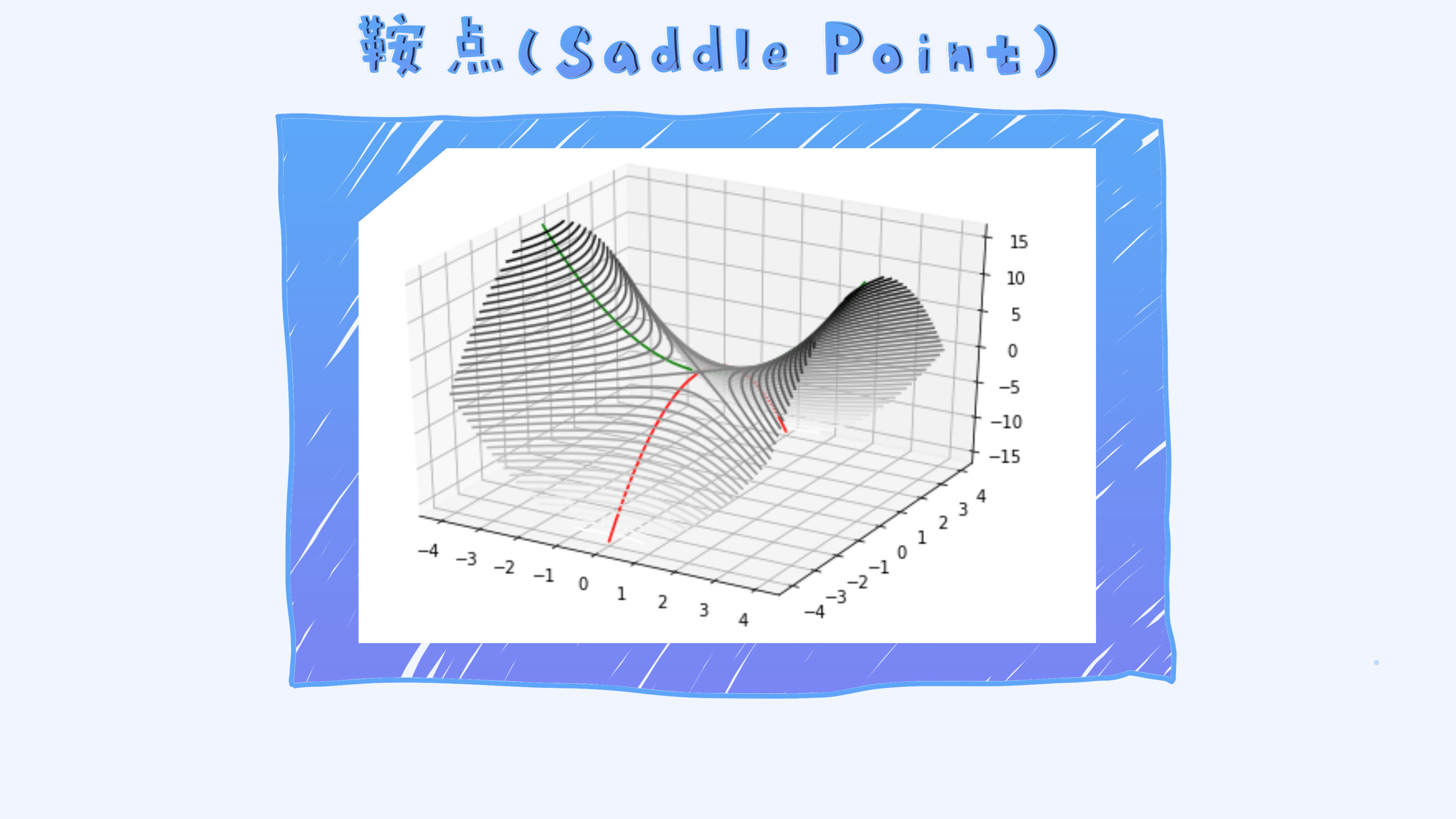
有一种类型的点叫做saddle point，它的梯度为0，但并不是局部最优解，如上面图里绿色和红色的相交点。

对于这些点，假如我们使用随机梯度下降法即可以较容易跳出并找到真正的局部最优解，因为随机梯度下降法本身具有噪声。

总之，在三者当中最常用的算法是小批量梯度下降法。特别是在深度学习当中，它的应用尤其重要。