这一节里，我们来学习一下如何构造逻辑回归的目标函数，以及优化这些参数。

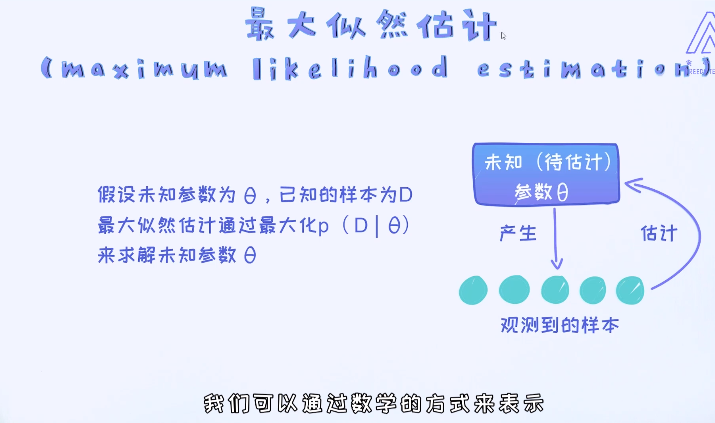
    理解如何构造目标函数，首先需要理解什么叫做最大似然，英文叫Maximum Likelihood。得到模型的最大似然之后，我们即可以通过优化的方式来得到最优的参数。

    对于逻辑回归，模型有两个参数，分别是w和b，前者是向量并表示每个特征的重要性，后者是偏移量(Intercept)。这些参数是需要去估计的。但现在我们唯一能拿到的是观测样本，这就意味着我们需要通过观测样本去估算最好的模型参数。

    这个问题也可以这么思考：有个未知的模型类似黑盒子，它产生了很多能看得见的样本。那这时候，我们其实可以通过最大化看到这些样本的概率来反推出模型最优的参数，这种方法叫做最大似然估计。

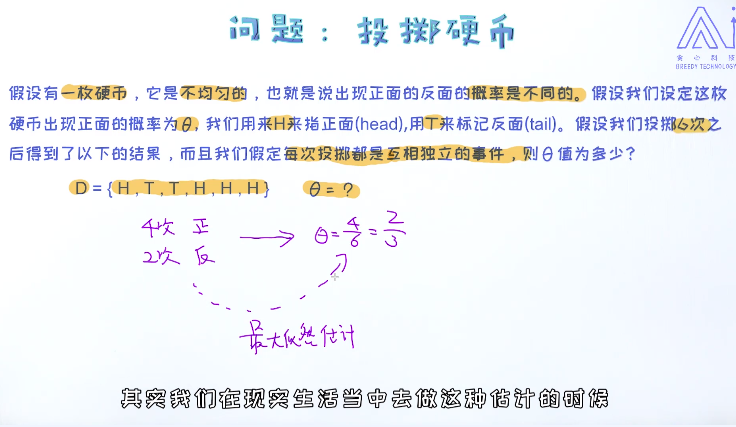
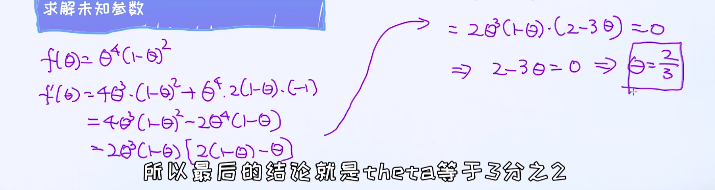
    image.png

    image.png

    image.png

    image.png

    image.png

    image.png

    image.png

    image.png

    接下来的问题是：对于逻辑回归模型如何构造最大似然？

    image.png

    条件概率部分前面已经了解，所以我们知道如何针对某一对样本写出其条件概率了。那对于最大似然，无非就是把所有的样本全部考虑进来。这里需要注意的一点是，这个总概率是由每一个条件概率的乘积来表示的。 随后，通过最大化这个条件概率来得出最优的参数w和b。

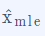
    这里有个image.png的符号。比如我们写了这样的一个式子:image.png， 它的意思是需要寻找让f(x)最大化的x值，并把这个值赋给image.png

    为什么这里可以使用乘积的方式来表示最大似然呢？ 而不是使用之和？


    其实这并不难理解，这里所使用的是叫做条件独立(conditional independence)的假设。在这个假设的前提下，可以把条件概率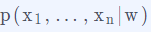image.png分解成image.png

    有了目标函数之后，我们的任务就比较明确了，就是需要寻找让目标函数最大化的参数ww和bb。 所以，接下来的问题就变成了一个经典的优化问题。

    image.png

    image.png
    log是个严格递增的函数，不会改变值

    最小化问题
    image.png