线性回归模型的矩阵表示法

当我们使用线性回归做预测的时候，或多或少肯定会存在误差的。当然没有任何误差是最理想的情况。

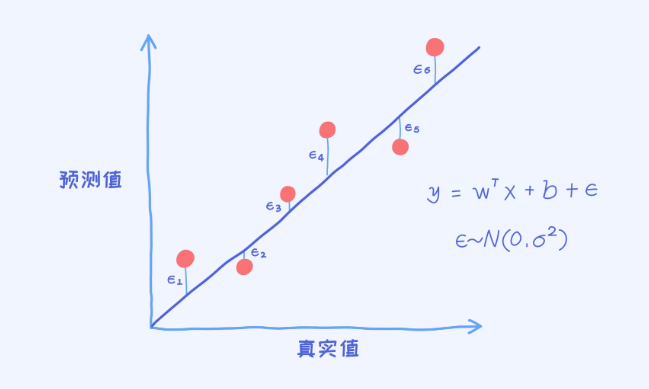
从误差的角度，我们可以引入一个误差变量叫做epsilonepsilon。是对于第i个样本的误差。

对于每一个样本的误差计算完之后再做个可视化，就可以得到上面的这幅图。

我们把误差看作是随机变量，在模型确定的条件下，每一个样本都对应一个误差值。那这时候的问题是：假如把所有样本的误差收集过来，那这些误差会具有什么样的特点呢？

根据大数定理，一旦样本个数越来越多，这些误差会慢慢服从正态分布。这就是最小二乘最核心的假设！

所以呢，假设误差变量epsilonepsilon服从正态分布，这样一来针对于每一个样本，我们可以得出如下的条件概率。

由于每一个样本的误差服从正态分布，所以在正态分布的基础上加一个确定的值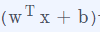也会服从正态分布，这是正态分布一个经典的性质。

之后，即可以把正态分布按照其定义来展开

上面是针对于一个样本的条件概率。当我们把所有样本全部考虑进来，并且假定每一个样本之间独立的时候，即可以得到对于整体样本的概率值。

如何针对于所有的样本构建最大似然概率：

所以结论就出来了，线性回归的最小二乘是跟高斯误差模型相对应的。如果我们把误差模型换成其他的分布，最终得出来的就不一定是最小二乘了。

上面一系列的分析过程，是从概率解释(Probabilistic Interpretation)的角度来分析的。通过这类分析，可以更深入地去理解目标函数背后的为什么(why)。

这通过一些数学的方式来把两个貌似不相关的概念联系了起来。其实，这是学习机器学习过程中特别重要的方法。通过这种学习方式，可以建立不同概念之间的联系，从而横向和纵向来打通知识体系。