困难
中等
简单
题目描述
给定长度分别为 m 和 n 的两个数组，其元素由 0-9 构成，表示两个自然数各位上的数字。现在从这两个数组中选出 k (k <= m + n) 个数字拼接成一个新的数，要求从同一个数组中取出的数字保持其在原数组中的相对顺序。

来源，leetcode 每日一题 321. 拼接最大数字

求满足该条件的最大数。结果返回一个表示该最大数的长度为 k 的数组。
说明: 请尽可能地优化你算法的时间和空间复杂度。
示例：

输入:
nums1 = [3, 4, 6, 5]
nums2 = [9, 1, 2, 5, 8, 3]
k = 5
输出:
[9, 8, 6, 5, 3]
输入:
nums1 = [6, 7]
nums2 = [6, 0, 4]
k = 5
输出:
[6, 7, 6, 0, 4]
输入:
nums1 = [3, 9]
nums2 = [8, 9]
k = 3
输出:
[9, 8, 9]

解题思路

相关题目：

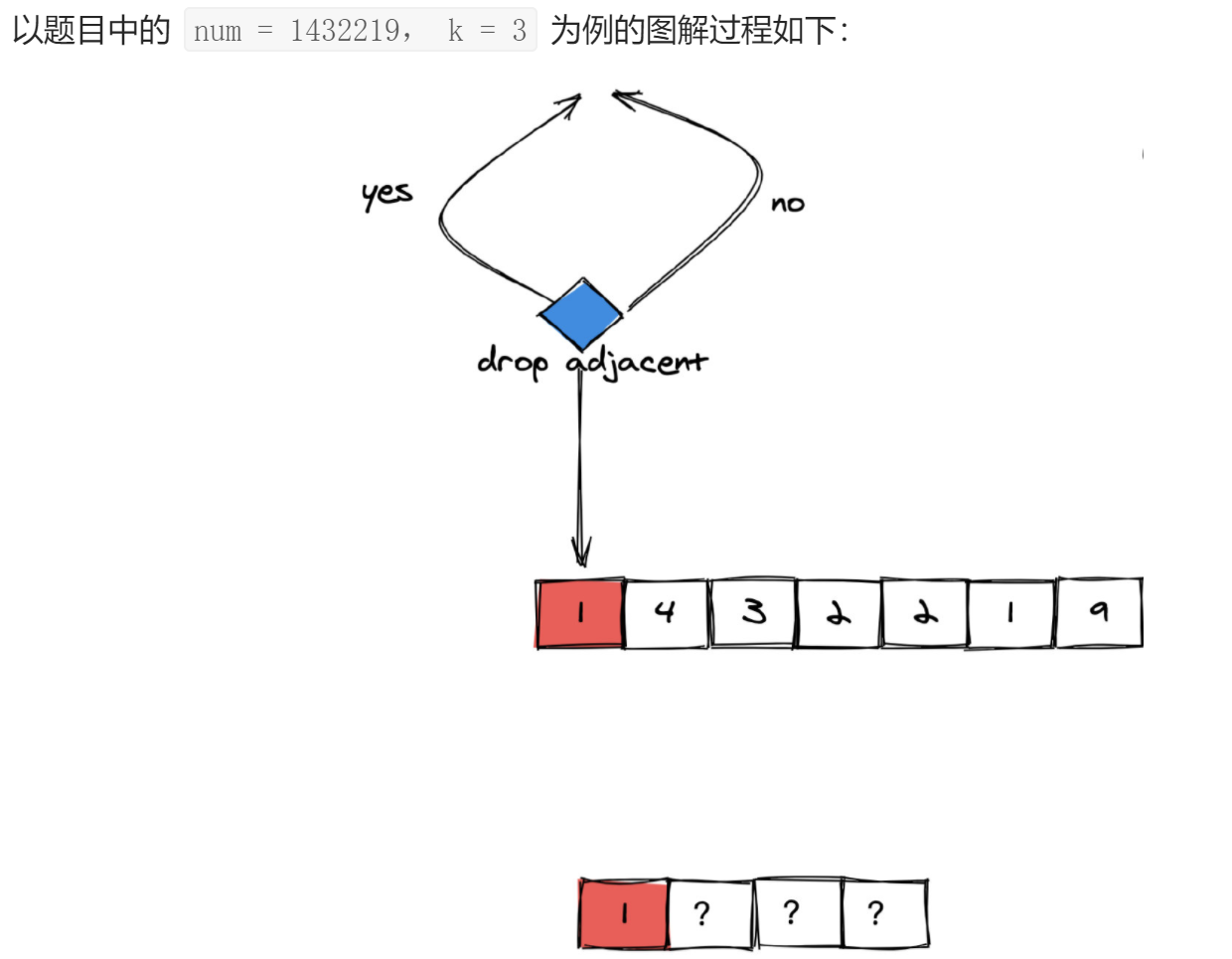
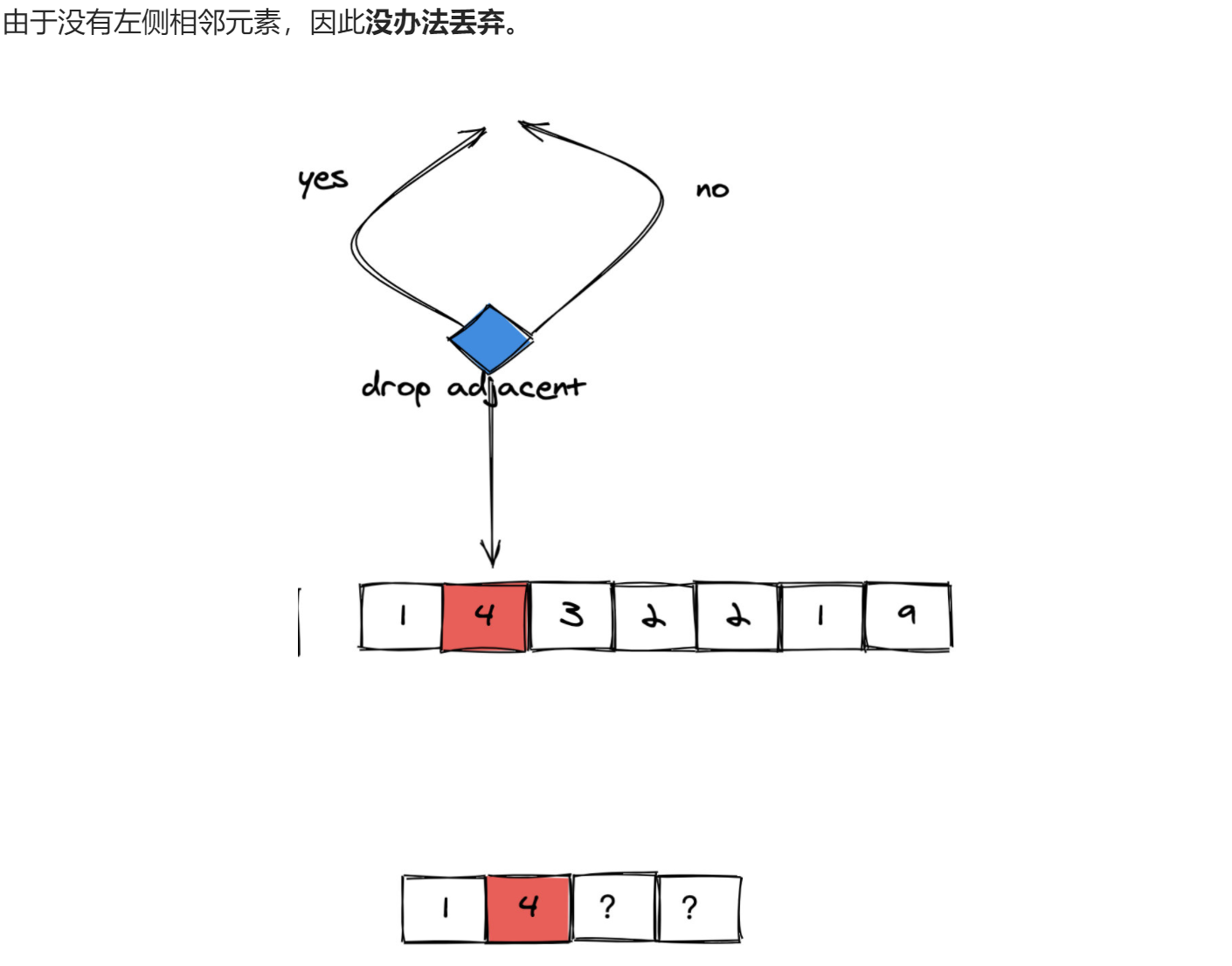
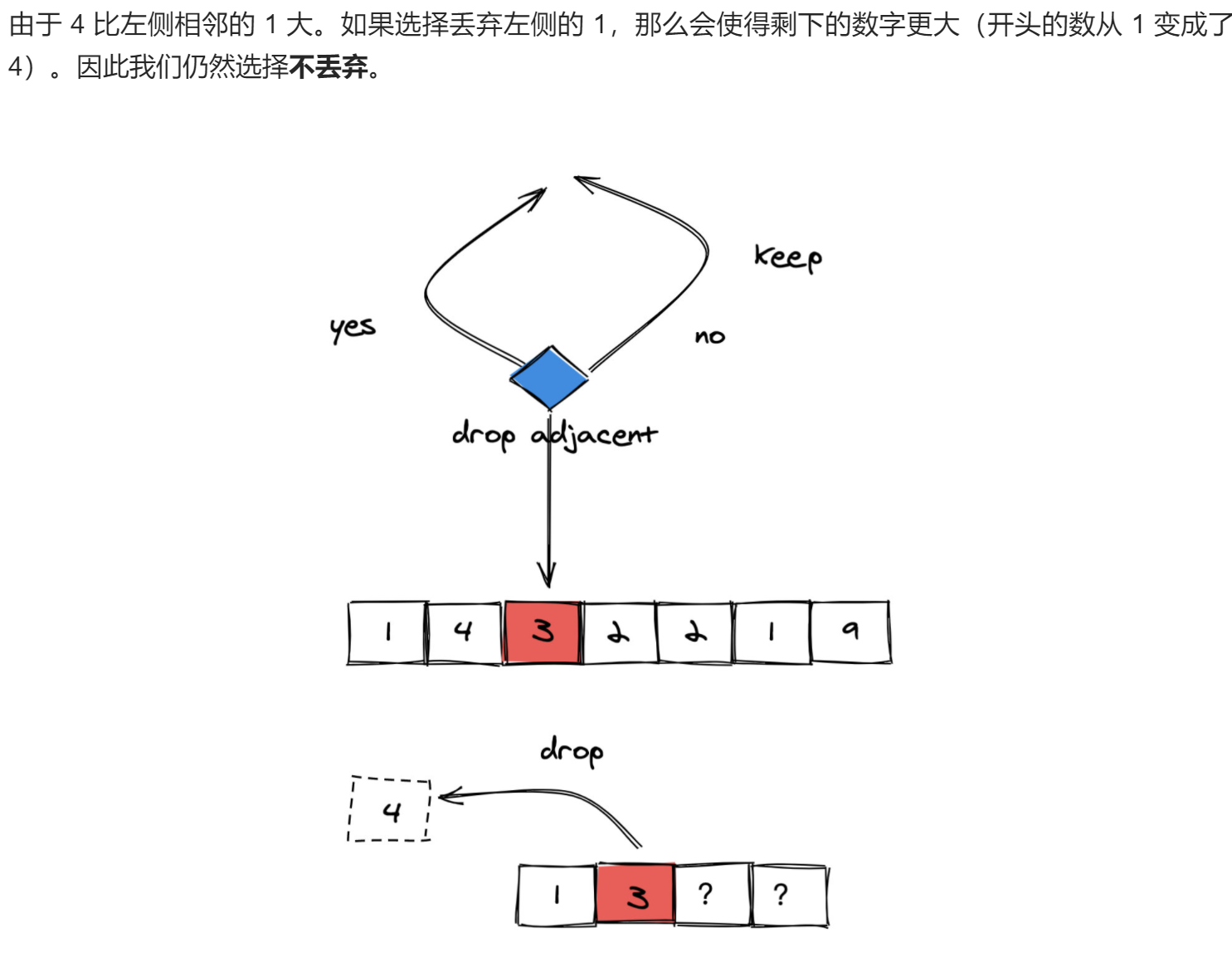
```cpp 给你一个仅包含小写字母的字符串，请你去除字符串中重复的字母，使得每个字母只出现一次。需保证返回结果的字典序最小（要求不能打乱其他字符的相对位置）。

示例 1:

输入: “bcabc” 输出: “abc” 示例 2:

输入: “cbacdcbc” 输出: “acdb”

![image.png](https://cdn.nlark.com/yuque/0/2020/png/183814/1608273260113-51ac877a-9076-4713-bd47-a9d9fab19ca9.png#align=left&display=inline&height=561&margin=%5Bobject%20Object%5D&name=image.png&originHeight=1121&originWidth=1501&size=252222&status=done&style=none&width=750.5)
<a name="ur5Ae"></a>
## 本题思路
![image.png](https://cdn.nlark.com/yuque/0/2020/png/183814/1608273296706-cb676994-d88e-427e-a01d-75e8d1dbce35.png#align=left&display=inline&height=589&margin=%5Bobject%20Object%5D&name=image.png&originHeight=1178&originWidth=1497&size=292462&status=done&style=none&width=748.5)
<a name="xZQIe"></a>
# 代码
```cpp
class Solution {
public:
    vector<int> maxNumber(vector<int>& nums1, vector<int>& nums2, int k) {
        int m = nums1.size(), n = nums2.size();
        vector<int> maxSubsequence(k, 0);
        int start = max(0, k - n), end = min(k, m);
        for (int i = start; i <= end; i++) {
            vector<int> subsequence1(MaxSubsequence(nums1, i));
            vector<int> subsequence2(MaxSubsequence(nums2, k - i));
            vector<int> curMaxSubsequence(merge(subsequence1, subsequence2));
            if (compare(curMaxSubsequence, 0, maxSubsequence, 0) > 0) {
                maxSubsequence.swap(curMaxSubsequence);
            }
        }
        return maxSubsequence;
    }
    vector<int> MaxSubsequence(vector<int>& nums, int k) {
        int length = nums.size();
        vector<int> stack(k, 0);
        int top = -1;
        int remain = length - k; // 需要抛弃的数量
        for (int i = 0; i < length; i++) {
            int num = nums[i];
            while (top >= 0 && stack[top] < num && remain > 0) { // 如果栈里有元素，且栈顶的元素小于当前元素，且还有需要抛弃的元素，则栈顶元素-1， 且需要抛弃的元素数量减一
                top--;
                remain--;
            }
            if (top < k - 1) { // 如果 栈未满，则直接入栈
                stack[++top] = num;
            } else {
                remain--; // 否则需要抛弃的元素数量减一
            }
        }
        return stack;
    }
    vector<int> merge(vector<int>& subsequence1, vector<int>& subsequence2) {
        int x = subsequence1.size(), y = subsequence2.size();
        if (x == 0) {
            return subsequence2;
        }
        if (y == 0) {
            return subsequence1;
        }
        int mergeLength = x + y;
        vector<int> merged(mergeLength);
        int index1 = 0, index2 = 0;
        for (int i = 0; i < mergeLength; i++) {
            if (compare(subsequence1, index1, subsequence2, index2) > 0) {
                merged[i] = subsequence1[index1++];
            } else {
                merged[i] = subsequence2[index2++];
            }
        }
        return merged;
    }
    int compare(vector<int>& subsequence1, int index1, vector<int>& subsequence2, int index2) {
        int x = subsequence1.size(), y = subsequence2.size();
        while (index1 < x && index2 < y) {
            int difference = subsequence1[index1] - subsequence2[index2];
            if (difference != 0) {
                return difference;
            }
            index1++;
            index2++;
        }
        return (x - index1) - (y - index2);
    }
};

Leetcode 每日一题

321. 拼接最大数字

题目描述

解题思路

总结